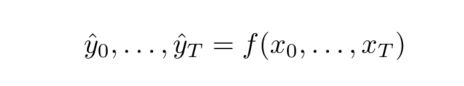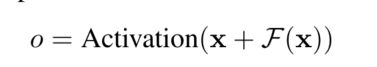tcn介绍
tcn 介绍
背景
对于大多数深度学习从业者来说,序列建模是递归网络的代名词。
然而,最近的结果表明,卷积架构在音频合成和机器翻译等任务上可以优于递归网络。给定一个新的序列建模任务或数据集,应该使用哪种架构?我们对用于序列建模的通用卷积和递归架构进行了系统评估。这些模型是在广泛的标准任务中评估的,这些任务通常用于对递归网络进行基准测试。我们的结果表明,简单的卷积架构在各种任务和数据集上都优于LSTM等经典递归网络,同时表现出更长的有效内存。我们得出的结论是,序列建模和递归网络之间的共同关联应该重新考虑,卷积网络应该被视为序列建模任务的自然起点。协助相关人员
小结:cnn可以进行序列建模,并且建模结果由于LSTM。
设计原理
序列整体建模
采用了第一性原理:具有简单性,将自回归预测与超长记忆相结合。
自回归预测,如公式(1),使用过去观测值来预测未来值,不能泄漏未来值来帮助预测。
更长的记忆力:RNN相比于传统的前馈神经网络的优点就是具有更长记忆力,因为其输入包含了隐藏模块。而CNN可以比于RNN的更好的竞争力也是具有更长的记忆力,所以可以用来进行序列建模。
递归神经网络(RNN)是一种能够处理序列数据的神经网络模型。相比于传统的前馈神经网络,RNN在处理序列数据时具有更长的记忆力,这是因为RNN中每个时间步的隐藏状态都是由当前输入和上一个时间步的隐藏状态共同决定的。这种记忆性使得RNN在处理长序列数据时有优势,并且在自然语言处理、语音识别、图像描述等领域有着广泛的应用。
RNN的记忆性的意义在于它使得模型可以在处理序列数据时考虑到之前的所有信息,而不仅仅是当前的输入。这样可以更好地捕捉序列数据中的长期依赖关系,例如在自然语言处理中,RNN可以更好地处理长句子中的语义关系。
在传统的前馈神经网络中,每个输入都只与当前的输出相关,而RNN则可以将之前的信息融入到当前的计算中,从而更好地反映序列数据的历史信息。同时,RNN还具有可重用的权重,这意味着模型可以在处理不同的序列数据时共享权重,从而在处理不同的任务时具有更好的泛化性能。
总之,RNN的记忆性对于处理序列数据具有重要意义,它可以更好地捕捉序列数据中的长期依赖关系,并且在处理不同的序列数据时具有更好的泛化性能。
具体操作-因果卷积(Casual Model)
- 由于需要满足自回归性,当前的输如仅与过去的输出相关,而不能由未来进行信息的泄漏。
- 并且序列要求输入与输出长度相同。采用了因果卷积操作。
可以更好捕捉时间序列中的因果关系,避免未来信息对当前信息的影响
因果卷积数学模型如下:
y t = ∑ i = 0 k − 1 w i ⋅ x t − i y_t = \sum_{i=0}^{k-1} w_i \cdot x_{t-i} yt=i=0∑k−1wi⋅xt−i
具体操作-膨胀卷积(Dilated convolutions)
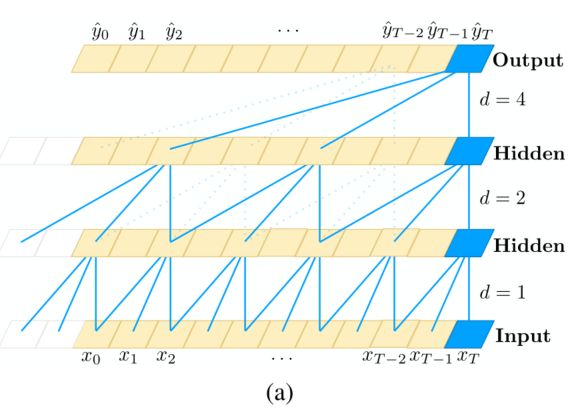
- 为了实现深入且长有效的历史,需要非常深入的神经网络或者非常大的滤波器。
- 这里采用了膨胀卷积,就是在卷积过程中插入一些空洞,用来增大感受视野,从而更好捕捉模型的长期依赖关系。
扩张卷积数学模型如下:
y t = ∑ i = 0 k − 1 w i ⋅ x ( r ⋅ t ) − ( r − 1 ) ⋅ i y_t = \sum_{i=0}^{k-1} w_i \cdot x_{(r \cdot t) - (r-1) \cdot i} yt=i=0∑k−1wi⋅x(r⋅t)−(r−1)⋅i
Input: [x1, x2, x3, x4, x5, x6, x7, x8, x9, x10]
| kernel |
| ↓ |
Output: [y1, y2, y3, y4, y5, y6, y7, y8]
y1 = w0*x1 + w1*x3 + w2*x5
y2 = w0*x2 + w1*x4 + w2*x6
y3 = w0*x3 + w1*x5 + w2*x7
y4 = w0*x4 + w1*x6 + w2*x8
y5 = w0*x5 + w1*x7 + w2*x9
y6 = w0*x6 + w1*x8 + w2*x10
y7 = w0*x7 + w1*x9
y8 = w0*x8 + w1*x10
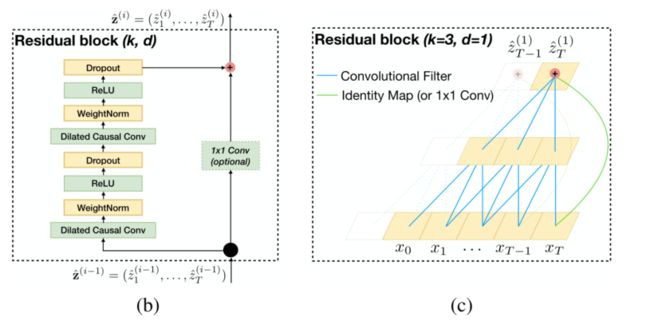
具体操作-残差连接
y = F ( x ) + x y = F(x) + x y=F(x)+x
将输入直接连接到输出,所以可以直接学习和输入之间的差异,而不是仅仅学习输出和映射之间关系。
- 可以减少梯度小时和梯度爆炸的问题,从而加速模型收敛速度。
x = input
y = Conv1D(x) + Conv1D(x)
y = BatchNormalization(y)
y = ReLU(y)
output = y + x
总结
- cnn可以用来进行序列建模,并且应该成为序列建模的首选。
- tcn采用了第一性原理:自回归性以及更长的记忆力可以满足序列建模的要求,并且性能优于rnn。
- tcn使用了因果卷积和膨胀卷积分别满足了上面的两个要求,并且使用了残差连接从而防止了梯度消失等问题,加速了模型的训练速度。