【从零开始写博客】数组运用:数组排序,字符串搜索和矩阵模拟(day2)
代码随想录刷题60天
【数组】Day1
目录
代码随想录刷题60天
引例一:
排序算法
直接插入(直接排序)
冒泡排序
双指针法
快速排序(递归法)
引例二
编辑
滑动窗口
引例三
总结与心得
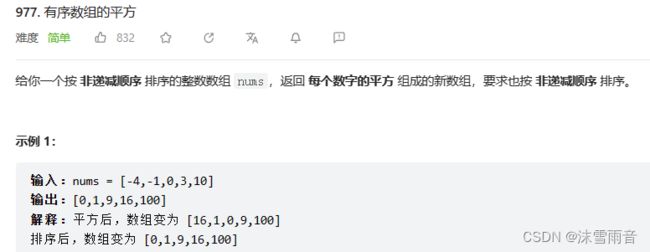
引例一:
该题为leetcode上一道简单难度的题,该题需要解决的问题是对已有数组中的数据进行平方处理后排序。其中数据的平方处理并非本体的重点所在,而重点在于对数组进行排序。因此对数据进行怎样排序才是本题的关键所在,笔者也将在下面介绍几种排序算法。
排序算法
直接插入(直接排序)
class Solution
{
public:
vector sortedSquares(vector& nums)
{
int temp,i,j;
nums[0] = nums[0] * nums[0];
for (i = 1; i < nums.size(); i++)
{
nums[i] = nums[i] * nums[i];
if (nums[i] < nums[i - 1])
{
temp = nums[i];
for (j = i - 1; j >= 0 && temp < nums[j]; j--)
//这里必须先判断j是否是负数,否则会造成数组角标错误
nums[j + 1] = nums[j];
nums[j + 1] = temp;//j超出了for循环的作用域,因此必须在开头声明。
}
}
return nums;
}
}; 冒泡排序
class Solution
{
public:
vector sortedSquares(vector& nums)
{
int temp,i,j;
nums[0] = nums[0] * nums[0];
for (i = 1; i < nums.size(); i++)
{
for (int j = 1; j < nums.size(); j++)
{
if (i == 1)
nums[j] = nums[j] * nums[j];
if (nums[j] < nums[j - 1])
{
int temp = nums[j - 1];
nums[j - 1] = nums[j];
nums[j] = temp;
}
}
}
return nums;
}
}; 以上两种排序是最基本的两种排序算法,也初学者最容易理解并写出的两种排序算法,但由于两种算法都使用两层for循环嵌套,所以时间复杂度都是n的平方,时间复杂度较高,所以从效率方面考虑,这两种算法是不够理想的。而接下来的两种方法通过借助一些手段从而将算法的复杂度降低。
双指针法
class Solution
{
public:
vector sortedSquares(vector& nums)
{
vector res(nums.size());
int i = 0, j = nums.size()-1;
int k = j;
while (i <= j)
{
if ((nums[i] * nums[i]) < (nums[j] * nums[j]))
res[k--] = (nums[j] * nums[j--]);
else
res[k--] = (nums[i] * nums[i++]);
}
return res;
}
}; 该方法利用了“原本数组元素中,成员都是有序排列”的这一条件来进行思考,我们可以发现当所有成员取平方时,其最大值一定会出现在数组的左界或右界,利用这一特点,每次将最大元素从左右端取出,用一个数组进行存储,便得到我们需要的结果。这种利用已有条件设计的排序方法在本题中是最优解。
快速排序(递归法)
int Paritition(int arr[],int low,int high){
int pivotLoc = arr[low];//将数组的第一个元素作为基准值
int temp;
while (low < high) {
while (low < high && arr[high] >= pivotLoc)
--high;//从右界开始,将第一个比基准值小的元素交换到左界(基准值于左界)
temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;//交换操作
while (low < high && arr[low] <= pivotLoc)
++low;//从
temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;//从左界开始,将第一个比基准值大的元素与基准值交换位置
}
return low;//返回此时的基准值角标
}
void QSort(int arr[], int n, int low, int hight) {
int pivotloc;
if (low < hight) {
pivotloc = Paritition(arr, low, hight);
QSort(arr, n, low, pivotloc - 1);
QSort(arr, n, pivotloc + 1, hight);
}
}快速排序算法定义了两个指针一个指向数组头m一个指向数组尾n,然后以头指针为基准值先从尾指针开始向后找比基准值小的元素,找的之后交换m,n所指向的值,此时n所指向的值就是基准值,m开始向后找,找到比基准值大的交换。
在数组元素本身无序的情况下,这种排序算法往往有着较高的效率。
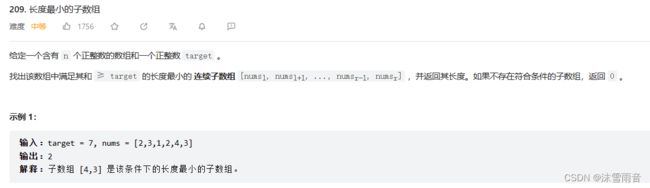
引例二
这道题有些类似于在字符串中寻找最长的连续相似字符。这道题我们当然可以使用暴力匹配进行处理,但这样处理在面对一些比较复杂的字符串时,往往效率不容乐观,因此我们可以借助一些巧妙方法来优化复杂度。
滑动窗口
class Solution
{
public:
int minSubArrayLen(int target, vector& nums)
{
int i=0, j;
int sum = 0;
int len = 0;
for (j = 0; j < nums.size(); j++)
{
sum += nums[j];
while (sum >= target)
{
if (len == 0)len = (j - i + 1);
len = len > (j - i + 1) ? (j - i + 1): len;
sum -= nums[i++];
}
}
return len;
}
}; 通过不断调整子数组的起始位置和终止位置,从而得到我们想要的结果。这种方法可以理解为双指针的一种。
引例三
该题不涉及算法,是一道典型的模拟题,我们需要通过模拟螺旋顺序打印其过程。本题也重点考察做题者对矩阵边界的理解程度。
具体实例代码如下
class Solution
{
public:
vector> generateMatrix(int n)
{
vector> res(n, vector(n, 0));
int loop = (n - 1) / 2 + 1;
int startX=0, startY=0;
int count = 1;
int offset = 0;
while (loop > 0)
{
int i, j;
for (i = startX; i < n - 1 - offset; i++)
res[startY][i] += count++;
for (j = startY; j < n - 1 - offset; j++)
res[j][i] += count++;
for (; i > 0 + offset; i--)
res[j][i] += count++;
for (; j > 0 + offset; j--)
res[j][i] += count++;
startX++;
startY++;
offset++;
loop--;
}
if (n / 2 == (n - 1) / 2)
res[n / 2][n / 2] = n * n;
//旋转矩阵最内层边长为1的矩阵由于“右开边界”而无法被赋值。
return res;
}
}; 总结与心得
· 在数组的各种问题中,对于数组边界开闭的理解会很大程度影响解决问题的思路。
· 在做题过程中,我们可以通过一些我们已知的方法与技巧来优化本题的思考逻辑,与此同时也需要根据题目已知信息来简化本题的思考逻辑。因此,我们需要在不断积累各种方法的同时也要学会就题解题。