特征点检测：CenSurE: Center Surround Extremas for Realtime Feature Detection and Matching

Reference:

1. CenSurE: Center Surround Extremas for Realtime Feature Detection and Matching

文章提出了一套尺度不变的中心环绕极值检测器(center-surround detectors: CenSurE)，并在稳定性(视点变化时的特征的持续性)和准确性(视点变化时特征的一致定位)上做了评估。(算法是个好算法，但是这文章写的有点烂，细节讲的很不清晰)

1. CenSurE 特征

该方法要求在所有尺度计算所有特征，并选择跨尺度和位置的极值。这种策略需要非常快的计算，在这里使用简化的双层内核作为中心环绕滤波器。主要关注点是寻找旋转不变但易于计算的 kernel。

1.1 寻找极值

该算法先在所有位置和尺度上计算简化的中心环绕滤波器，并找到局部领域中的极值。再通过使用 Harris 度量+消除那些具有弱边缘响应的的方式过滤极值点。

1.2 二级滤波

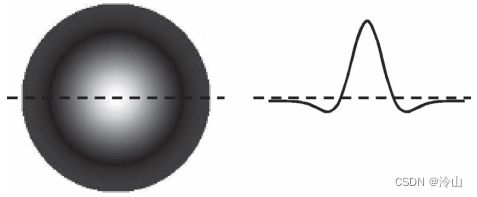
Lowe 在 SIFT 中使用 DoG(Difference of Gaussian) 来近似 LoG(Laplacian of Gaussian) ，但我们寻求更简单的近似，使用双层的中心环绕滤波器，也就是说，它们将图像值乘以 $1$ 或 $-1$。下图显示了具有不同程度对称性的一系列双层滤波器。圆形滤波器最近似拉普拉斯算子，但最难计算。其他滤波器可以使用积分图快速计算，并且从八边形到六边形再到盒式滤波器的计算成本逐渐降低。我们研究了两个端点：八边形用于更好的性能，而盒式用于更小的计算量。

1.3 使用盒式的 CenSurE

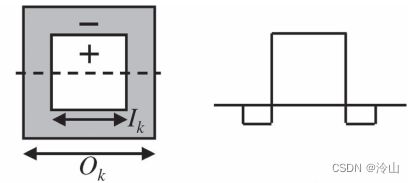
用正方形替换圆形 BLoG 中的两个圆圈(上左图)，形成 CenSurE-DOB。这生成了基础的中心环绕哈尔小波(center-surround Haar wavelet)。Figure 1(d) 显示了块大小为 $n$ 的通用中心环绕小波。内盒的大小为 $(2n+1)\times (2n+1)$，外盒的大小为 $(4n+1)\times (4n+1)$。卷积是通过乘法和求和完成的。如果 $I_n$ 是内部权重、$O_n$ 是外盒权重，那么为了使该滤波器的 $DC$ 相应为零，我们必须有：
$$O_n(4n+1{)}^2=I_n(2n+1{)}^2\text{\hspace{1em}(1)}$$我们还必须对跨尺度的每个小波的面积差进行标准化(毕竟使用的面积大小不同，面积大的得到的响应还是更大一些)：
$$I_n(2n+1{)}^2=I_{n+1}(2(n+1)+1{)}^2\text{\hspace{1em}(2)}$$我们对中心环绕 Haar 小波使用一组七个尺度，分别为块大小 $n=[1,2,3,4,5,6,7]$。由于块大小 $1$ 和 $7$ 是边界，因此检测到的特征的最小尺度对应的块大小为 $2$。(这里啥意思？$1$ 的不就是最小的么)这大致对应与 $\sigma$ 大小为 $1.885$ 的 LoG。 这五个尺度涵盖了 $2\frac{1}{2}$ 的 octave，尽管尺度是线性的。当然添加更多的块大小，如 $8$、$9$ 等也很容易。

2.4 使用八角形的 CenSurE

盒形的差分显然不是旋转不变的内核。特别的，DOB 在$45°$ 平面内旋转的表现不佳。另一方面，八边形更接近圆形，并且比 DOB 更好的近似 LoG。

在使用八边形时，通过内部和外部加权相加执行卷积的基本思想保持不变。与 DOB 中一样，必须找到权重 $I_n$ 和 $O_n$，使得 DC 响应为 $0$ 并且所有滤波器都根据八边形的面积进行标准化。

如 Figure 1(b)所示，八边形可以用垂直边(m)的高度和倾斜边(n)来表示。

2.5 非最大值抑制

我们计算图像中每个像素的七个滤波器响应。然后我们在尺度空间上执行非极大值抑制------简而言之，如果响应大于(最大情况)或小于(最小情况)其在局部邻域中的相邻响应，则响应被抑制。该领域中的最大值或最小值的像素是特征点位置。我们使用 $3\times 3\times 3$ 领域进行非极大值抑制。

滤波器响应的大小给出了特征强度的指示。强度越大，越有可能被重复。弱响应很可能不稳定。因此，我们可以应用一个阈值来过滤掉弱响应。

由于我们所有的响应都是在原始图像上计算的，没有进行下采样，所以我们所有的特征位置都很好地定位，并且我们不需要执行子像素插值。

2.6 线抑制

沿着边缘或线的特征很难定位，因此它们不太稳定。这种定义不佳的峰值沿直线的主曲率很大，但垂直方向的主曲率很小，因此可以使用主曲率之比过滤掉。使用特定尺度下响应函数的二阶矩矩阵来过滤掉这些响应：
$$H=\left[\begin{array}{cc}\sum L_x^2& \sum L_x{L}_y\\ \sum L_x{L}_y& \sum L_y^2\end{array}\right]\text{\hspace{1em}(3)}$$$L_x$ 和 $L_y$ 是响应函数 $L$ 沿 $x$ 和 $y$ 方向的导数。在一个窗口上进行求和，该窗口线性依赖于特定特征点的尺度：尺度越高，窗口大小越大。注意这是尺度自适应的 Harris 度量，它与 SIFT 用于过滤线相应的 Hessian 矩阵不同。一旦计算出 Harris 度量，它的迹接行列式就可以用来计算主曲率之比。我们对该比率使用阈值 $10$，并在块大小为 $2$ 的最小尺度上使用 $9\times 9$ 窗口。

Harris 度量的计算成本比 SIFT 使用的 Hessian 矩阵计算量更大。然而，这种度量只需要计算一小部分特征点，即响应超过阈值的尺度空间最大值，因此不存在计算瓶颈。根据我们经验，它在抑制线响应方面比 Hessian 做得更好。

1.7 滤波器计算

CenSurE 的关键是能够有效地计算所有尺寸的双层滤波器。盒子滤波器可以使用积分图来完成。积分图 $I$ 是图像的中间表示，包含图像 $N$ 的高度 $y$ 和宽度 $x$ 的灰度像素值之和，即：
$$I(x,y)=\sum _{x^{\prime }=0}^x\sum _{y^{\prime }=0}^{y}N\left(x^{\prime },y^{\prime }\right)\text{\hspace{1em}(4)}$$积分图是递归计算的，只需要对图像进行一次扫描。一旦计算出积分图，只需四次加减法即可计算任何矩形区域的光强和，计算量与图像大小无关(就加减法计算而言)。

修改后的积分图可以用来计算其他多边形滤波器。这里的想法是，任何梯形面积都可以在常数时间内计算，使用两个不同的倾斜积分图的组合，其中像素的和表示角度面积和。倾斜程度由参数 $\alpha$ 控制：
$$I_{\alpha }(x,y)=\sum _{y^{\prime }=0}^y\sum _{x^{\prime }=0}^{x+\alpha \left(y-y^{\prime }\right)}N\left(x^{\prime },y^{\prime }\right)\text{\hspace{1em}(5)}$$当 $\alpha =0$，这就是标准的矩形积分图。当 $\alpha <0$ 时，求和面积向左倾斜；当 $\alpha >0$ 时，求和面积向右倾斜(Fig.2, left)。利用增量技术可以使计算斜积分图像和矩形积分图像时间相同。

将具有相同斜度的两个区域加在一起，确定具有平行水平边的梯形的一端(Fig.2, right)；另一端是类似的，使用不同的倾斜。每个梯形需要三个加法，就像矩形的情况一样。最后，多边形滤波器可以分解为1个(盒形)、2个(六边形)和3个(八边形)梯形，这是计算这些滤波器的相对成本。

2. OpenCV 中的 cv::StarDetector 类

OpenCV 中实现的 CenSurE 算法称为 STAR 算法，对 CenSurE 算法进行了一些改进。

1. STAR 滤波器的形状是两个交错重叠的正方形，构成一个八角形。
   

2. STAR 算法选择 17个尺度递增的检测器 $n=[1,2,3,4,6,8,11,12,16,23,32,45,46,64,90,128,-1]$

3. 滤波器的卷积运算基于积分图，但没有直接计算八角形的强度和，而是分别用积分图像和倾斜积分图分别计算后相加。

   StarDetector 类的构造函数为：

   /*!
    The "Star" Detector.
   
    The class implements the keypoint detector introduced by K. Konolige.
    */
   class StarDetectorImpl : public StarDetector
   {
   public:
       //! the full constructor
       StarDetectorImpl(int _maxSize=45, int _responseThreshold=30,
                            int _lineThresholdProjected=10,
                            int _lineThresholdBinarized=8,
                            int _suppressNonmaxSize=5);
   
       void detect( InputArray image, std::vector<KeyPoint>& keypoints, InputArray mask=noArray() ) CV_OVERRIDE;
   
   protected:
       int maxSize;
       int responseThreshold;
       int lineThresholdProjected;
       int lineThresholdBinarized;
       int suppressNonmaxSize;
   };
   

这套源码写的感觉也有点不太行，最好自行修改一下：

• 代码内为了加速计算，忽略 $size=1,2,max$ 的情况，将它们取负了：

  sizes1[0] = -sizes1[0];
  sizes1[1] = -sizes1[1];
  sizes1[maxIdx] = -sizes1[maxIdx];

  后面再做过滤：

  featureSize = s_ptr[maxPt.y*sstep + maxPt.x]) >= 4

  问题在于可能有相近 response 但是稍微小一点的会被忽略。建议在选取 scale 做计算时直接去掉小的 scale。