LearnOpenGL学习笔记——几何着色器
几何着色器
在顶点和片段着色器之间有一个可选的几何着色器(Geometry Shader),几何着色器的输入是一个图元(如点或三角形)的一组顶点。几何着色器可以在顶点发送到下一着色器阶段之前对它们随意变换。然而,几何着色器最有趣的地方在于,它能够将(这一组)顶点变换为完全不同的图元,并且还能生成比原来更多的顶点。废话不多说,我们直接先看一个几何着色器的例子:
#version 330 core
layout (points) in;
layout (line_strip, max_vertices = 2) out;
void main() {
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
EmitVertex();
gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
EmitVertex();
EndPrimitive();
}
在几何着色器的顶部,我们需要声明从顶点着色器输入的图元类型。这需要在in关键字前声明一个布局修饰符(Layout Qualifier)。这个输入布局修饰符可以从顶点着色器接收下列任何一个图元值:
- points:绘制GL_POINTS图元时(1)。
- lines:绘制GL_LINES或GL_LINE_STRIP时(2)
- lines_adjacency:GL_LINES_ADJACENCY或GL_LINE_STRIP_ADJACENCY(4)
- triangles:GL_TRIANGLES、GL_TRIANGLE_STRIP或GL_TRIANGLE_FAN(3)
- triangles_adjacency:GL_TRIANGLES_ADJACENCY或GL_TRIANGLE_STRIP_ADJACENCY(6)
以上是能提供给glDrawArrays渲染函数的几乎所有图元了。如果我们想要将顶点绘制为GL_TRIANGLES,我们就要将输入修饰符设置为triangles。括号内的数字表示的是一个图元所包含的最小顶点数。接下来,我们还需要指定几何着色器输出的图元类型,这需要在out关键字前面加一个布局修饰符。和输入布局修饰符一样,输出布局修饰符也可以接受几个图元值: - points
- line_strip
- triangle_strip
有了这3个输出修饰符,我们就可以使用输入图元创建几乎任意的形状了。要生成一个三角形的话,我们将输出定义为triangle_strip,并输出3个顶点。
几何着色器同时希望我们设置一个它最大能够输出的顶点数量(如果你超过了这个值,OpenGL将不会绘制多出的顶点),这个也可以在out关键字的布局修饰符中设置。在这个例子中,我们将输出一个line_strip,并将最大顶点数设置为2个。如果你不知道什么是线条(Line Strip):线条连接了一组点,形成一条连续的线,它最少要由两个点来组成。在渲染函数中每多加一个点,就会在这个点与前一个点之间形成一条新的线。在下面这张图中,我们有5个顶点:
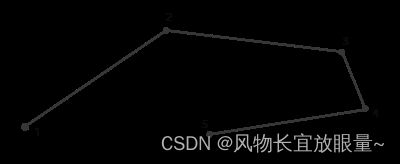
如果使用的是上面定义的着色器,那么这将只能输出一条线段,因为最大顶点数等于2。为了生成更有意义的结果,我们需要某种方式来获取前一着色器阶段的输出。GLSL提供给我们一个内建(Built-in)变量,在内部看起来(可能)是这样的:
in gl_Vertex
{
vec4 gl_Position;
float gl_PointSize;
float gl_ClipDistance[];
} gl_in[];
这里,它被声明为一个接口块(Interface Block,我们在上一节已经讨论过),它包含了几个很有意思的变量,其中最有趣的一个是gl_Position,它是和顶点着色器输出非常相似的一个向量。
要注意的是,它被声明为一个数组,因为大多数的渲染图元包含多于1个的顶点,而几何着色器的输入是一个图元的所有顶点。
有了之前顶点着色器阶段的顶点数据,我们就可以使用2个几何着色器函数,EmitVertex和EndPrimitive,来生成新的数据了。几何着色器希望你能够生成并输出至少一个定义为输出的图元。在我们的例子中,我们需要至少生成一个线条图元。
void main() {
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
EmitVertex();
gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
EmitVertex();
EndPrimitive();
}
每次我们调用EmitVertex时,gl_Position中的向量会被添加到图元中来。当EndPrimitive被调用时,所有发射出的(Emitted)顶点都会合成为指定的输出渲染图元。在一个或多个EmitVertex调用之后重复调用EndPrimitive能够生成多个图元。在这个例子中,我们发射了两个顶点,它们从原始顶点位置平移了一段距离,之后调用了EndPrimitive,将这两个顶点合成为一个包含两个顶点的线条。现在你(大概)了解了几何着色器的工作方式,你可能已经猜出这个几何着色器是做什么的了。它接受一个点图元作为输入,以这个点为中心,创建一条水平的线图元。如果我们渲染它,看起来会是这样的:

目前还并没有什么令人惊叹的效果,但考虑到这个输出是通过调用下面的渲染函数来生成的,它还是很有意思的:
glDrawArrays(GL_POINTS, 0, 4);
使用几何着色器
简单的场景
为了展示几何着色器的用法,我们将会渲染一个非常简单的场景,我们只会在标准化设备坐标的z平面上绘制四个点。这些点的坐标是:
float points[] = {
-0.5f, 0.5f, // 左上
0.5f, 0.5f, // 右上
0.5f, -0.5f, // 右下
-0.5f, -0.5f // 左下
};
顶点着色器只需要在z平面绘制点就可以了,所以我们将使用一个最基本顶点着色器:
#version 330 core
layout (location = 0) in vec2 aPos;
void main()
{
gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0);
}
#version 330 core
out vec4 FragColor;
void main()
{
FragColor = vec4(0.0, 1.0, 0.0, 1.0);
}
我们将会创建一个传递(Pass-through)几何着色器,它会接收一个点图元,并直接将它传递(Pass)到下一个着色器:
#version 330 core
layout (points) in;
layout (points, max_vertices = 1) out;
void main() {
gl_Position = gl_in[0].gl_Position;
EmitVertex();
EndPrimitive();
}
和顶点与片段着色器一样,几何着色器也需要编译和链接,但这次在创建着色器时我们将会使用GL_GEOMETRY_SHADER作为着色器类型:
geometryShader = glCreateShader(GL_GEOMETRY_SHADER);
glShaderSource(geometryShader, 1, &gShaderCode, NULL);
glCompileShader(geometryShader);
...
glAttachShader(program, geometryShader);
glLinkProgram(program);
这和没使用几何着色器时是完全一样的!我承认这是有点无聊,但既然我们仍然能够绘制这些点,所以几何着色器是正常工作的,现在是时候做点更有趣的东西了!
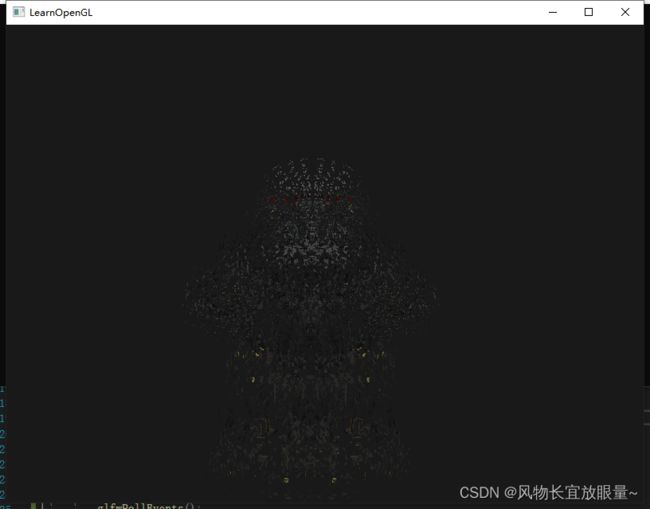
爆破物体
当我们说爆破一个物体时,我们并不是指要将宝贵的顶点集给炸掉,我们是要将每个三角形沿着法向量的方向移动一小段时间。效果就是,整个物体看起来像是沿着每个三角形的法线向量爆炸一样。这样的几何着色器效果的一个好处就是,无论物体有多复杂,它都能够应用上去。
因为我们想要沿着三角形的法向量位移每个顶点,我们首先需要计算这个法向量。我们所要做的是计算垂直于三角形表面的向量,仅使用我们能够访问的3个顶点。你可能还记得在变换小节中,我们使用叉乘来获取垂直于其它两个向量的一个向量。如果我们能够获取两个平行于三角形表面的向量a和b,我们就能够对这两个向量进行叉乘来获取法向量了。下面这个几何着色器函数做的正是这个,来使用3个输入顶点坐标来获取法向量:
vec3 GetNormal()
{
vec3 a = vec3(gl_in[0].gl_Position) - vec3(gl_in[1].gl_Position);
vec3 b = vec3(gl_in[2].gl_Position) - vec3(gl_in[1].gl_Position);
return normalize(cross(a, b));
}
这里我们使用减法获取了两个平行于三角形表面的向量a和b。因为两个向量相减能够得到这两个向量之间的差值,并且三个点都位于三角平面上,对任意两个向量相减都能够得到一个平行于平面的向量。注意,如果我们交换了cross函数中a和b的位置,我们会得到一个指向相反方向的法向量——这里的顺序很重要!
vec4 explode(vec4 position, vec3 normal)
{
float magnitude = 2.0;
vec3 direction = normal * ((sin(time) + 1.0) / 2.0) * magnitude;
return position + vec4(direction, 0.0);
}
当使用我们的模型加载器绘制一个模型时,爆破(Explode)效果的完整几何着色器是这样的:
#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices = 3) out;
in VS_OUT {
vec2 texCoords;
} gs_in[];
out vec2 TexCoords;
uniform float time;
vec4 explode(vec4 position, vec3 normal) { ... }
vec3 GetNormal() { ... }
void main() {
vec3 normal = GetNormal();
gl_Position = explode(gl_in[0].gl_Position, normal);
TexCoords = gs_in[0].texCoords;
EmitVertex();
gl_Position = explode(gl_in[1].gl_Position, normal);
TexCoords = gs_in[1].texCoords;
EmitVertex();
gl_Position = explode(gl_in[2].gl_Position, normal);
TexCoords = gs_in[2].texCoords;
EmitVertex();
EndPrimitive();
}
法向量可视化
在这一部分中,我们将使用几何着色器来实现一个真正有用的例子:显示任意物体的法向量。当编写光照着色器时,你可能会最终会得到一些奇怪的视觉输出,但又很难确定导致问题的原因。光照错误很常见的原因就是法向量错误,这可能是由于不正确加载顶点数据、错误地将它们定义为顶点属性或在着色器中不正确地管理所导致的。我们想要的是使用某种方式来检测提供的法向量是正确的。检测法向量是否正确的一个很好的方式就是对它们进行可视化,几何着色器正是实现这一目的非常有用的工具。
思路是这样的:我们首先不使用几何着色器正常绘制场景。然后再次绘制场景,但这次只显示通过几何着色器生成法向量。几何着色器接收一个三角形图元,并沿着法向量生成三条线——每个顶点一个法向量。伪代码看起来会像是这样:
shader.use();
DrawScene();
normalDisplayShader.use();
DrawScene();
这次在几何着色器中,我们会使用模型提供的顶点法线,而不是自己生成,为了适配(观察和模型矩阵的)缩放和旋转,我们在将法线变换到裁剪空间坐标之前,先使用法线矩阵变换一次(几何着色器接受的位置向量是剪裁空间坐标,所以我们应该将法向量变换到相同的空间中)。这可以在顶点着色器中完成:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
out VS_OUT {
vec3 normal;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
void main()
{
gl_Position = projection * view * model * vec4(aPos, 1.0);
mat3 normalMatrix = mat3(transpose(inverse(view * model)));
vs_out.normal = normalize(vec3(projection * vec4(normalMatrix * aNormal, 0.0)));
}
变换后的裁剪空间法向量会以接口块的形式传递到下个着色器阶段。接下来,几何着色器会接收每一个顶点(包括一个位置向量和一个法向量),并在每个位置向量处绘制一个法线向量:
#version 330 core
layout (triangles) in;
layout (line_strip, max_vertices = 6) out;
in VS_OUT {
vec3 normal;
} gs_in[];
//像这样的几何着色器应该很容易理解了。注意我们将法向量乘以了一个MAGNITUDE向量,来限制显示出的法向量大小(否则它们就有点大了)。
const float MAGNITUDE = 0.4;
void GenerateLine(int index)
{
gl_Position = gl_in[index].gl_Position;
EmitVertex();
gl_Position = gl_in[index].gl_Position + vec4(gs_in[index].normal, 0.0) * MAGNITUDE;
EmitVertex();
EndPrimitive();
}
void main()
{
GenerateLine(0); // 第一个顶点法线
GenerateLine(1); // 第二个顶点法线
GenerateLine(2); // 第三个顶点法线
}
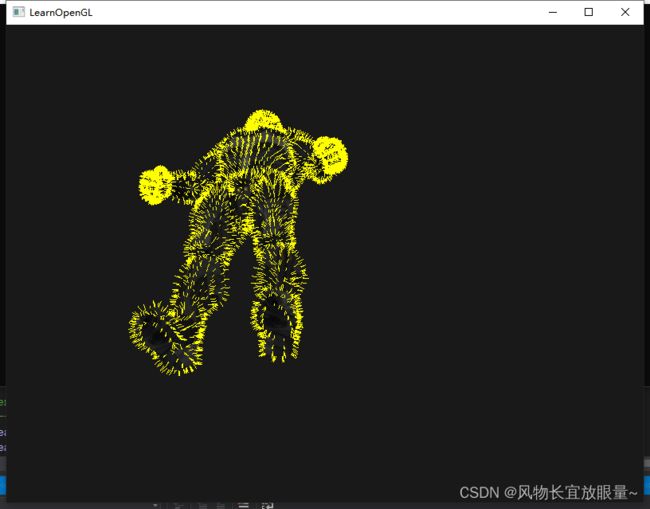
因为法线的可视化通常都是用于调试目的,我们可以使用片段着色器,将它们显示为单色的线(如果你愿意也可以是非常好看的线):
#version 330 core
out vec4 FragColor;
void main()
{
FragColor = vec4(1.0, 1.0, 0.0, 1.0);
}
知识点总结:
1.什么是几何着色器
2.几何着色器输入声明和输出声明
3.GLSL 给我们提供了内建变量gl_in[]
4.EmitVertex 和 EndPrimitive
5.如何爆破物体(使用几何着色器)
6.如何让法向量可视化(使用几何着色器)
https://learnopengl-cn.github.io/04%20Advanced%20OpenGL/09%20Geometry%20Shader/