violet~evergarden

AcWing-C/C++语法基础【合集1】

文章目录

重点练习题目链接fast-challenge
1.变量、输入输出、表达式与顺序语句
- 604. 圆的面积
- 605. 简单乘积
- 606. 平均数1
- 607. 平均数2
- 608. 差
- 609. 工资
- 610. 工资和奖金
- 611. 简单计算
- 612. 球的体积
- 613. 面积
- 614. 最大值
- 615. 油耗
- 616. 两点间的距离
- 617. 距离
- 618. 燃料消耗
2.判断语句
- 653. 钞票
- 654. 时间转换
- 655. 天数转换
- 656. 钞票和硬币
- 657. 选择练习
- 658. 一元二次方程公式
- 659. 区间
- 660. 零食
- 661. 平均数
- 662. 点的坐标
- 663. 简单排序
- 664. 三角形
- 665. 倍数
- 666. 三角形类型
- 667. 游戏时间
- 668. 游戏时间
- 669. 加薪
- 670. 动物
- 671. DDD
- 672. 税
3.循环语句
- 708. 偶数
- 709. 奇数
- 710. 六个奇数
- 711. 乘法表
- 712. 正数
- 713. 区间
- 714. 连续奇数的和
- 715. 余数
- 716. 最大数和它的位置
- 717. 简单斐波那契
- 718. 实验
- 719. 连续奇数的和
- 720. 连续整数相加
- 721. 递增序列
- 722. 数字序列和它的和
- 723. PUM
- 724. 约数
- 725. 完全数
- 726. 质数
- 727. 菱形 [曼哈顿距离]
4.数组
- 737. 数组替换
- 738. 数组填充
- 739. 数组选择
- 740. 数组变换
- 741. 斐波那契数列
- 742. 最小数和它的位置
- 743. 数组中的行
- 744. 数组中的列
- 745. 数组的右上半部分
- 746. 数组的左下半部分
- 747. 数组的左上半部分
- 748. 数组的右下半部分
- 749. 数组的上方区域
- 750. 数组的下方区域
- 751. 数组的左方区域
- 752. 数组的右方区域
- 753. 平方矩阵 I
- 754. 平方矩阵 II
- 755. 平方矩阵 III
- *756. 蛇形矩阵
⑤字符串⑥函数⑦结构体⑧数组-跳转【合集2】

fast-open题目

重点练习题目链接fast-challenge

1.变量、输入输出、表达式与顺序语句

604. 圆的面积

计算圆的面积的公式定义为 A=πR2。

请利用这个公式计算所给圆的面积。

π 的取值为 3.14159。

输入格式
输入包含一个浮点数，为圆的半径 R。

输出格式
输出格式为 A=X，其中 X 为圆的面积，用浮点数表示，保留四位小数。

数据范围
0 输入样例：
2.00
输出样例：
A=12.5664

#include

using namespace std;

int main()
{
    double r;//小数优先double，减小精度损失
    cin >> r;
    printf("A=%.4lf\n", r * 3.14159 * r);//常量直接使用或const double pi = 3.14159
    //cout<<"A="<
    
    return 0;
}

fixed + setprecision()

#include 
   cout << fixed << setprecision(保留小数点后的位数); //可以先定义，直到下一次变换前都是此格式【作用域】 
   cout << setprecision(总共显示的位数) << endl;

605. 简单乘积

读取两个整数值。

在此之后，计算它们的乘积并将结果存储在名为 PROD 的变量中。

输出结果如下例所示。

输入格式
共两行，每行包含一个整数。

输出格式
输出格式为 PROD = X，其中 X 为乘积结果。

数据范围
输入的两个整数的绝对值均不超过 10000。

输入样例：
3
9
输出样例：
PROD = 27

#include
using namespace std;

vector<int> mul(vector<int> &A,int b) {
	vector<int> C;

	int t = 0;//进位
	for(int i = 0; i < A.size() || t; i++) { //【清除前导0】    C的最后一位是 乘积的第一位 
		if(i < A.size()) t += A[i] * b;
		C.push_back(t % 10);//只取t的个位
		t /= 10;//整除10后是进位
	}
	
	while (C.size() > 1 && C.back() == 0) C.pop_back();//【清除前导0】    C的最后一位是 乘积的第一位 
	
	return C;
}

int main() {

	string a;
	int b;
	cin >> a >> b;

	vector<int> A,C;
	for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0'); //a[i] 里面存的是字符型整数，要转化为真正的整数 需减去 '0' 成int型

	C = mul(A,b);

	for(int i = C.size() - 1; i >= 0; i--) printf("%d",C[i]);

	return 0;
}

606. 平均数1

读取两个浮点数 A 和 B 的值，对应于两个学生的成绩。

请你计算学生的平均分，其中 A 的成绩的权重为 3.5，B 的成绩的权重为 7.5。

成绩的取值范围在 0 到 10 之间，且均保留一位小数。

输入格式
输入占两行，每行包含一个浮点数，第一行表示 A，第二行表示 B。

输出格式
输出格式为 MEDIA = X，其中 X 为平均分，结果保留五位小数。

数据范围
0≤A,B≤10.0
输入样例：
5.0
7.1
输出样例：
MEDIA = 6.43182

double ==> %lf

#include

using namespace std;

double a,b;
int main()
{

    scanf("%lf%lf",&a,&b);//double -- 输入%lf

    printf("MEDIA = %.5lf",(a*3.5 +b*7.5) / 11);  //3.5+7.5 == 11

    return 0;
}

607. 平均数2

读取三个浮点数 A，B 和 C 的值，对应于三个学生的成绩。

请你计算学生的平均分，其中 A 的成绩的权重为 2，B 的成绩的权重为 3，C 的成绩的权值为 5。

成绩的取值范围在 0 到 10 之间，且均保留一位小数。

输入格式
输入共三行，每行包含一个浮点数，第一行表示 A，第二行表示 B，第三行表示 C。

输出格式
输出格式为 MEDIA = X，其中 X 为平均分，结果保留一位小数。

数据范围
0≤A,B,C≤10.0,

输入样例：
5.0
6.0
7.0
输出样例：
MEDIA = 6.3

double读入用cin简单,而用scanf对应%lf

#include 
#include

using namespace std;

int main() 
{
    double a, b, c;
    scanf("%lf%lf%lf", &a, &b, &c);//如果输入类型不匹配，不会赋值 如用%d, 都为0不变
    printf("MEDIA = %.1lf\n", (double)(a * 2 + b * 3 + c * 5) / 10);

    return 0;

}

608. 差

读取四个整数 A,B,C,D，并计算 (A×B−C×D) 的值。

输入格式
输入共四行，第一行包含整数 A，第二行包含整数 B，第三行包含整数 C，第四行包含整数 D。

输出格式
输出格式为 DIFERENCA = X，其中 X 为 (A×B−C×D) 的结果。

数据范围
−10000≤A,B,C,D≤10000
输入样例：
5
6
7
8
输出样例：
DIFERENCA = -26

#include

using namespace std;

int a,b,c,d;

int main()
{
    scanf("%d%d%d%d", &a, &b, &c, &d);

    printf("DIFERENCA = %d", a * b - c * d);

    return 0;
}

609. 工资

请编写一个程序，可以读取一名员工的员工编号，本月工作总时长（小时）以及时薪，并输出他的工资条，工资条中包括员工编号和员工月收入。

输入格式
输入包含两个整数和一个浮点数，分别代表员工编号，工作时长以及时薪。

每个数占一行。

输出格式
输出共两行，第一行格式为 NUMBER = X，其中 X 为员工编号。

第二行格式为 SALARY = U$ Y，其中 Y 为该员工月收入，保留两位小数。

数据范围
1≤员工编号≤100,
1≤总工作时长≤200,
1≤时薪≤50
输入样例：
25
100
5.50
输出样例：
NUMBER = 25
SALARY = U$ 550.00

#include
using namespace std;

int a,b;
double c;
int main()
{
    scanf("%d%d%lf", &a, &b, &c);
    
    printf("NUMBER = %d\nSALARY = U$ %.2lf", a, (double)b * c); //输出
        
    return 0;
}

610. 工资和奖金

请你编写一个程序，给定你一个销售人员的名字，底薪以及月销售额。

请你计算他的月收入是多少。

已知月收入等于底薪加 15% 的月销售额。

所有数据保留两位小数。

输入格式
输入第一行包含一个由大写字母构成的长度不超过 10 的字符串，表示销售人员的名字。

第二行包含一个浮点数，表示该人员的底薪。

第三行包含一个浮点数，表示该人员的月销售额。

输出格式
输出格式为 TOTAL = R$ X，X 为该人员月收入。

数据范围
0≤底薪，月销售额≤10000.00
输入样例：
JOAO
500.00
1000.00
输出样例：
TOTAL = R$ 650.00

#include 

using namespace std;

char a[10];

int main()
{

    double b, c;

    scanf("%s %lf %lf", a, &b, &c);
    printf("TOTAL = R$ %.2lf", b + c * 0.15);

    return 0;
}

611. 简单计算

给定你两个产品的产品编号，产品数量以及产品单价。

请你计算买下两种产品一共需要花费多少钱。

输入格式
输入共两行。

每行包含两个整数以及一个浮点数，表示其中一件产品的产品编号，产品数量以及产品单价。

输出格式
输出格式为 VALOR A PAGAR: R$ X，其中 X 为产品总价值，保留两位小数。

数据范围
1≤产品编号,产品数量≤10000,
1.00≤产品单价≤10000.00
输入样例：
12 1 5.30
16 2 5.10
输出样例：
VALOR A PAGAR: R$ 15.50

#include
using namespace std;

int idx[2],n[2];
double val[2];
int main()
{
    scanf("%d%d%lf%d%d%lf", &idx[0], &n[0], &val[0], &idx[1], &n[1], &val[1]);
    
    printf("VALOR A PAGAR: R$ %.2lf",double(n[0] * val[0] + n[1] * val[1]));
        
    return 0;
}

612. 球的体积

给定你一个球体的半径 R，请你计算球体的体积。

计算球体的公式为 V=(4/3)∗π∗R3。

π 取 3.14159。

注意：有些语言中 (4/3) 无法得到 1.3333…，建议在公式中使用 (4/3.0)。

输入格式
输入一个整数 R。

输出格式
输出格式为 VOLUME = X，其中 X 为球体的体积，结果保留三位小数。

数据范围
1≤R≤2000
输入样例：
3
输出样例：
VOLUME = 113.097

#include

using namespace std;

int main() 
{
    int r; 
    scanf("%d", &r);
    printf("VOLUME = %.3f", 4 / 3.0 * 3.14159 * r * r * r);

    return 0;
}

613. 面积

给定三个浮点数 A，B 和 C。

然后，计算如下图形的面积：

底边为 A，高为 C 的三角形。
半径 C 的圆。（π=3.14159）
底边为 A 和 B，高为 C 的梯形。
边长为 B 的正方形。
边长为 A 和 B 的长方形。
输入格式
输入共一行，包含三个保留一位小数的浮点数 A，B，C。

输出格式
输出共五行，形式如下所示：

第一行，格式为 TRIANGULO: X，其中 X 为所求三角形面积。

第二行，格式为 CIRCULO: X，其中 X 为所求圆形面积。

第三行，格式为 TRAPEZIO: X，其中 X 为所求梯形面积。

第四行，格式为 QUADRADO: X，其中 X 为所求正方形面积。

第五行，格式为 RETANGULO: X，其中 X 为所求长方形面积。

所有答案保留三位小数。

数据范围
0≤A,B,C≤10000.0
输入样例：
3.0 4.0 5.2
输出样例：
TRIANGULO: 7.800
CIRCULO: 84.949
TRAPEZIO: 18.200
QUADRADO: 16.000
RETANGULO: 12.000

< cmath > : acos(-1)
#include
#include

using namespace std;

const double PI = acos(-1);//反三角函数 [此题规定了取π = 3.14159【不能用acos(-1)】]
int main() 
{
    //printf("%.16lf\n", PI);
    double a, b, c;
    scanf("%lf%lf%lf", &a, &b, &c);
    printf("TRIANGULO: %.3f\n", a * c / 2);
    printf("CIRCULO: %.3f\n", 3.14159 * c * c);
    printf("TRAPEZIO: %.3f\n", (a + b) * c / 2);
    printf("QUADRADO: %.3f\n", b * b);
    printf("RETANGULO: %.3f\n", a * b);

    return 0;
}

614. 最大值

给定三个整数，请你找出它们中的最大值。

下列公式可能对你有所帮助：

$max(a,b)=\dfrac{(a+b+abs(a−b))}{2}$
输入格式
输入占一行，包含三个整数。

输出格式
输出格式为 X eh o maior，其中 X 为三个数中的最大值。

数据范围
1≤给定整数≤10⁹
输入样例：
7 14 106
输出样例：
106 eh o maior

c++11 : max{a, b, c}

#include 
#include 

using namespace std;

int a, b, c;
int res;


int main(){

    scanf("%d%d%d", &a, &b, &c);
    //res = max( max(a,b) , c );
    res = max({a, b, c});//c++11
    printf("%d eh o maior", res);

    return 0;
}

公式法：

#include 

using namespace std;

int a, b, c;

int main(){

    scanf("%d%d%d", &a, &b, &c);
    int maxv = 0;
    maxv = (a + b + abs(a - b)) / 2 ;//max(a, b) == (a + b + abs(a - b)) / 2
    maxv = (maxv + c + abs(maxv - c)) / 2; 

    printf("%d eh o maior", maxv);

    return 0;
}

615. 油耗

给定一个汽车行驶的总路程（km）和消耗的油量（l），请你求出汽车每消耗 1 升汽油可行驶多少公里路程。

输入格式
输入共两行，第一行包含整数 X，表示行驶总路程。

第二行包含保留一位小数的浮点数 Y，表示消耗的油量。

输出格式
输出格式为 M km/l，其中 M 为计算结果，保留三位小数。

数据范围
1≤X,Y≤10⁹
输入样例：
500
35.0
输出样例：
14.286 km/l

#include
using namespace std;


int main()
{
    int x;
    double y;
    scanf("%d%lf", &x, &y);
    printf("%.3lf km/l", x / y);

    return 0;
}

616. 两点间的距离

给定两个点 P1 和 P2，其中 P1 的坐标为 (x1,y1)，P2 的坐标为 (x2,y2)，请你计算两点间的距离是多少。
$distance=\sqrt{ (x2−x1)^2+(y2−y1)^2 }$
输入格式
输入共两行，每行包含两个双精度浮点数 xi,yi，表示其中一个点的坐标。

输入数值均保留一位小数。

输出格式
输出你的结果，保留四位小数。

数据范围
−10⁹≤xi,yi≤10⁹
输入样例：
1.0 7.0
5.0 9.0
输出样例：
4.4721

y1库函数名，放全局冲突error

#include
#include

using namespace std;

int main()
{
    
    double x1,y1,x2,y2;//y1库函数名，放全局冲突error
    scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
    
    printf( "%.4lf",sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))  );
        
    return 0;
}

617. 距离

两辆汽车在同一地点，同时，沿同一方向前进。

一辆车的速度为 60 km/h，另一辆车的速度为 90 km/h。

显然，快车与慢车的距离会不断拉开，每过一个小时（60 分钟），两车的距离就拉开 30 公里。

现在，告诉你两车之间的距离为 L 公里，请你求出两车已经行驶了多长时间？

输入格式
输入包含一个整数 L，表示两车之间的距离。

输出格式
输出格式为 X minutos，其中 X 为已经行驶的时间，单位为分钟。

数据范围
1≤L≤10⁹
输入样例：
30
输出样例：
60 minutos

L *= 2 等价于： L <<= 1

#include 

using namespace std;

int L;   //L == 2*X

int main() {
    scanf("%d", &L);
    printf("%d minutos", L << 1);
    return 0;
}

618. 燃料消耗

一辆汽车每行驶 12 公里需要消耗 1 升汽油，现在告诉你该汽车的行驶速度 S（km/h）和行驶时间 T（h），请你计算该车在行驶过程中一共消耗了多少升汽油。

输入格式
输入共两行，第一行包含一个整数 T，表示行驶时间（h）。

第二行包含一个整数 S，表示行驶速度（km/h）。

输出格式
输出行驶期间的总油耗，结果保留三位小数。

数据范围
1≤T,S≤10⁷
输入样例：
10
85
输出样例：
70.833

long long
隐式转换(long long)(a * b) / 12.0 -->浮点型long

#include 

using namespace std;

int main()
{   //long double a, b会变0【因为无法读入,没有赋值】
    long long a, b;
    cin >> a >> b;
    printf("%.3lf\n", a * b / 12.0);
    return 0;
}

fixed + setprecision()

#include 
   cout << fixed << setprecision(保留小数点后的位数); //可以先定义，直到下一次变换前都是此格式【作用域】 
   cout << setprecision(总共显示的位数) << endl;

2.判断语句

653. 钞票

在这个问题中，你需要读取一个整数值并将其分解为多张钞票的和，每种面值的钞票可以使用多张，并要求所用的钞票数量尽可能少。

请你输出读取值和钞票清单。

钞票的可能面值有 100,50,20,10,5,2,1。

输入格式
输入一个整数 N。

输出格式
参照输出样例，输出读取数值以及每种面值的钞票的需求数量。

数据范围
0 输入样例：
576
输出样例：
576
5 nota(s) de R$ 100,00
1 nota(s) de R$ 50,00
1 nota(s) de R$ 20,00
0 nota(s) de R$ 10,00
1 nota(s) de R$ 5,00
0 nota(s) de R$ 2,00
1 nota(s) de R$ 1,00

#include
using namespace std;

int a;
int money[] = {100,50,20,10,5,2,1 };
int main()
{
    
    
    scanf("%d",&a);   
    printf("%d\n",a);
    for(int i = 0;i < 7;i++)
    
    {
        printf("%d nota(s) de R$ %d,00\n",a/money[i],money[i]);   // ,00 逗笑了
        a %= money[i];
    }

    return 0;
}

654. 时间转换

读取一个整数值，它是工厂中某个事件的持续时间（以秒为单位），请你将其转换为小时：分钟：秒来表示。

输入格式
输入一个整数 N。

输出格式
输出转换后的时间表示，格式为 hours:minutes:seconds。

数据范围
1≤N≤1000000
输入样例：
556
输出样例：
0:9:16

#include
#include

using namespace std;

int n;
int main()
{
    scanf("%d",&n); // s能直接除以60，因为都是60进制 ，而年月日进制不同
    int h = n / 3600,m = n % 3600 / 60,s = n % 60; // 取最低位： % ， 取最高位 ： / 
    printf("%d:%d:%d",h,m,s);

    return 0;
}

c++版


#include 

using namespace std;

int main()
{
    int t;
    cin >> t;
    int h = t / 3600, m = t % 3600 / 60, s = t % 60;
    cout << h << ':' << m << ':' << s << endl;
    return 0;
}

655. 天数转换

读取对应于一个人的年龄（以天为单位）的整数值，并转化为年，月和日表示方式输出，年、月、日分别对应 ano(s), mes(es), dia(s)。

注意：为了方便计算，假设全年 365 天，每月 30 天。数据保证，不会出现 12 个月和几天的情况，例如 360,363 或 364。

输入格式
输入一个整数 N。

输出格式
参照输出样例，输出转换后的天数表达。

数据范围
1≤N≤1000000
输入样例：
400
输出样例：
1 ano(s)
1 mes(es)
5 dia(s)

①% x 映射[0, x-1]
②n / x : 含有多少个x

#include

using namespace std;

int y, m, d;

int main()
{
    int n;
    scanf("%d", &n);
    int y = n / 365 , m = n % 365 / 30 , d = n % 365 % 30 ;
    printf("%d ano(s)\n%d mes(es)\n%d dia(s)\n", y, m, d);
    
    return 0;
}

c++版

#include
using namespace std;
int n,y,m,d;
int main()
{
    cin>>n;
    y=n/365;
    m=n%365/30;
    d=n%365%30;
    cout<<fixed<<setprecision(0)<<y<<" ano(s)"<<endl<<m<<" mes(es)"<<endl<<d<<" dia(s)";
}

copy不好用

#include 
using namespace std;
int main()
{
    int n;
    cin >> n;
    printf("%d ano(s)\n", n / 365);
    n -= n / 365 * 365;
    printf("%d mes(es)\n", n / 30);
    n -= n / 30 * 30;
    printf("%d dia(s)\n", n);
    return 0;
}

656. 钞票和硬币

读取一个带有两个小数位的浮点数，这代表货币价值。

在此之后，将该值分解为多种钞票与硬币的和，每种面值的钞票和硬币使用数量不限，要求使用的钞票和硬币的数量尽可能少。

钞票的面值是 100,50,20,10,5,2。

硬币的面值是 1,0.50,0.25,0.10,0.05 和 0.01。

输入格式
输入一个浮点数 N。

输出格式
参照输出样例，输出每种面值的钞票和硬币的需求数量。

数据范围
0≤N≤1000000.00
输入样例：
576.73
输出样例：
NOTAS:
5 nota(s) de R$ 100.00
1 nota(s) de R$ 50.00
1 nota(s) de R$ 20.00
0 nota(s) de R$ 10.00
1 nota(s) de R$ 5.00
0 nota(s) de R$ 2.00
MOEDAS:
1 moeda(s) de R$ 1.00
1 moeda(s) de R$ 0.50
0 moeda(s) de R$ 0.25
2 moeda(s) de R$ 0.10
0 moeda(s) de R$ 0.05
3 moeda(s) de R$ 0.01

小数移位变整数
如两位小数：先乘 100 再除 100 【对应运算也要对应放缩】

#include

using namespace std;

double a[] = {100,50,20,10,5,2};
double b[] = {100,50,25,10,5,1}; //先100后面再除100
int main()
{
    double m;
    cin >> m;//m有两位小数点

    int n = m * 100;//把m转化成整数n

    puts("NOTAS:");
    for (int i = 0; i < 6; i ++ )
    {
        printf("%d nota(s) de R$ %.2lf\n", n / a[i] / 100, (double)a[i]);
        n %= a[i] * 100;
    }

    puts("MOEDAS:");
    for (int i = 0; i < 6; i ++ )
    {
        printf("%d moeda(s) de R$ %.2lf\n", n / b[i], (double)b[i] / 100);
        n %= b[i];
    }
    return 0;
}

之前的代码

#include
using namespace std;

const int N=10;

int b[N],c[N];

int main()
{
    double s[7]={0,100,50,20,10,5,2};
    double p[7]={0,1.00,0.50,0.25,0.10,0.05,0.010};
    double a;
    cin>>a;
    for(int i=1;i<=6;i++)
    {
        b[i] = a / s[i];
        a -= (s[i] * b[i]);
    }
    for(int i=1;i<=6;i++)
    {
        double x=a/p[i];
        c[i]=(int)(x+0.00001);//防止了精度问题
        a = a - (c[i] * p[i]);
    }
    puts("NOTAS:");
    for(int i=1;i<=6;i++)
    {
        printf("%d nota(s) de R$ %.2lf\n",b[i],s[i]);
    }
    puts("MOEDAS:");
    for(int i=1;i<=6;i++)
    {
        printf("%d moeda(s) de R$ %.2lf\n",c[i],p[i]);
    }
    return 0; 
}

657. 选择练习

读取 4 个整数值 A，B，C 和 D。

如果四个整数同时满足以下条件：

B 大于 C。
D 大于 A。
C 和 D 的总和大于 A 和 B 的总和。
C 和 D 是正值。
A 是偶数。
则输出 Valores aceitos，否则，输出 Valores nao aceitos。

输入格式
输入占一行，包含四个整数 A,B,C,D。

输出格式
如果输入数值满足题目条件则输出 Valores aceitos，否则输出 Valores nao aceitos。

数据范围
−100≤A,B,C,D≤100
输入样例：
5 6 7 8
输出样例：
Valores nao aceitos

#include

using namespace std;

int main()
{
    int a, b, c, d;
    scanf("%d%d%d%d", &a, &b, &c, &d);
    if(b > c && d > a && c + d > a + b && c > 0 && d > 0 && a % 2 == 0) puts("Valores aceitos");
    else puts("Valores nao aceitos");
    return 0;
}

658. 一元二次方程公式

读取三个浮点数 a,b,c 的值，利用一元二次方程求根公式对方程 ax2+bx+c=0 进行求解。

一元二次方程求根公式为：
$x=\frac{−b±\sqrt{b^2−4ac}}{2a}$
如果 b²−4ac<0 导致方程无解或 a=0，则输出 Impossivel calcular。

输入格式
输入三个浮点数 a,b,c。

输出格式
参照输出格式，输出方程的根，输出结果保留五位小数，如果无解则输出 Impossivel calcular。

两个根可以按任意顺序输出，都算正确。

数据保证不存在只有一个解的情况。

数据范围
−1000.0≤a,b,c≤1000.0
输入样例：
10.0 20.1 5.1
输出样例：
R1 = -0.29788
R2 = -1.71212

#include
#include
#include

using namespace std;

int main()
{
    double a,b,c,d,x1,x2;
    cin >> a >> b >> c;
    d = b * b - 4 * a * c;
    if(d > 0&& a != 0)
    {
        x1 = (-b + sqrt(d)) / (2 * a);
        x2 = (-b - sqrt(d)) / (2 * a);
        printf("R1 = %.5lf\nR2 = %.5lf\n", x1, x2);  //cout<}
    else if(d < 0|| a == 0)
    {
        cout<<"Impossivel calcular";
    }
}

659. 区间

给定一个浮点数，请你判断该数字属于以下哪个区间：[0,25],(25,50],(50,75],(75,100]。

如果给定的数值小于 0 或大于 100，则程序输出 Fora de intervalo，表示超出范围。

开区间 (a,b)：在实数 a 和实数 b 之间的所有实数，但不包含 a 和 b。

闭区间 [a,b]：在实数 a 和实数 b 之间的所有实数，包含 a 和 b。

输入格式
输入一个浮点数。

输出格式
判断输入数值位于哪个区间，按格式 Intervalo x 输出，其中 x 为区间范围 [0,25],(25,50],(50,75],(75,100] 中的一个。

如果数值位于所有区间之外，则输出 Fora de intervalo。

输入样例：
25.01
输出样例：
Intervalo (25,50]

映射法
向上取整ceil() : ceil(1.1) = 2;

#include
#include//ceil

using namespace std;
//此版存储判断，但消耗空间 ，但联系到了映射，以及ceil向上取整
string s[4]={"[0,25]","(25,50]","(50,75]","(75,100]"};
double a;

int main()
{
    cin>>a;
    a=ceil(a);//对浮点数【向上取整】

    if(a < 0 || a > 100)
        cout<<"Fora de intervalo";
    else if(a == 0)
        cout<<"Intervalo [0,25]";
    else
        cout<<"Intervalo "<<s[((int)a - 1) / 25];  //映射成下标0-3 
}

朴素法


#include 
#include 

using namespace std;

int main()
{
    double n;
    cin >> n;
    if (n < 0 || n > 100)
        puts("Fora de intervalo");
    else if (n <= 25)
        puts("Intervalo [0,25]");
    else if (n <= 50)
        puts("Intervalo (25,50]");
    else if (n <= 75)
        puts("Intervalo (50,75]");
    else
        puts("Intervalo (75,100]");
    return 0;
}

660. 零食

某商店出售 5 种零食，零食编号为 1∼5。

5 种零食的价目表如下所示：

零食种类价格
零食 1 R$ 4.00
零食 2 R$ 4.50
零食 3 R$ 5.00
零食 4 R$ 2.00
零食 5 R$ 1.50
现在给定某种零食的编号和数量，请你计算总价值是多少。

输入格式
输入包含两个整数 x 和 y，其中 x 为零食编号，y 为零食数量。

输出格式
输出格式为 Total: R$ X，其中 X 为总价值，保留两位小数。

数据范围
1≤x≤5,
1≤y≤100
输入样例：
3 2
输出样例：
Total: R$ 10.00

#include

using namespace std;
//double类型  
double val[]= {0, 4.00, 4.50, 5.00, 2.00, 1.50};    //第一位初始0：从1开始
int a,b;
int main()
{

    scanf("%d%d", &a, &b);//(int)下标 * 数量

    printf("Total: R$ %.2lf", val[a] * b); //double  > int

    return 0;
}

661. 平均数

读取 4 个数字 N1,N2,N3,N4，这 4 个数字都是保留 1 位小数的浮点数，对应于学生获得的 4 个分数。

这 4 个分数的权重分别为 2,3,4,1，请你计算学生成绩的平均值 X 并输出 Media: X。

接下来分为以下三种情况：

如果平均值为 7.0 或更高，则输出 Aluno aprovado.。
如果平均值小于 5.0，则输出 Aluno reprovado.。
如果平均值大于等于 5.0 并且小于 7.0，则输出 Aluno em exame.，并再读取一个数字 Y，然后输出 Nota do exame: Y。接下来重新计算平均值 Z=(X+Y)/2，如果 Z 大于或等于 5.0，则输出 Aluno aprovado.，否则输出 Aluno reprovado.。最后输出 Media final: Z，表示学生的最终成绩。
输入格式
输入中包含四个浮点数，表示学生的四个成绩。

也有部分满足情况 3 的数据，多包含一个浮点数。

输出格式
输出的结果均保留 1 位小数，具体形式参照题目描述和输出样例。

数据范围
0≤输入数据≤10.0
输入样例1：
2.0 4.0 7.5 8.0
6.4
输出样例1：
Media: 5.4
Aluno em exame.
Nota do exame: 6.4
Aluno aprovado.
Media final: 5.9
输入样例2：
2.0 6.6 4.0 9.0
输出样例2：
Media: 4.9
Aluno reprovado.
输入样例3：
9.0 4.0 8.5 9.0
输出样例3：
Media: 7.3
Aluno aprovado.

math库：round(x) : 四舍五入 round(1.5) = 2.0

c++

#include 

using namespace std;

int main()
{
    double n1, n2, n3, n4;

    cin >> n1 >> n2 >> n3 >> n4;

    double x = (n1 * 2 + n2 * 3 + n3 * 4 + n4 * 1) / 10;
    printf("Media: %.1lf\n", x);
    if (x >= 7) puts("Aluno aprovado.");
    else if (x < 5) puts("Aluno reprovado.");
    else
    {
        puts("Aluno em exame.");
        double y;
        cin >> y;
        printf("Nota do exame: %.1lf\n", y);
        double z = (x + y) / 2;
        if (z >= 5) puts("Aluno aprovado.");
        else puts("Aluno reprovado.");
        printf("Media final: %.1lf\n", z);
    }

    return 0;
}

#include

using namespace std;

int main()
{
    double n1, n2, n3, n4;    
    scanf("%lf%lf%lf%lf", &n1, &n2, &n3, &n4);
    double x = (n1 * 2 + n2 * 3 + n3 * 4 + n4 * 1) / (2 + 3 + 4 + 1);
    printf("Media: %.1lf\n", x);
    if(x > 7.0)
    {
        puts("Aluno aprovado.");
    }
    else if(x < 5.0)
    {
        puts("Aluno reprovado.");
    }
    else// if(x > 5.0 && x < 7.0) 
    {
        puts("Aluno em exame.");
        double y;
        scanf("%lf", &y);
        printf("Nota do exame: %.1lf\n", y);
        double z = (x + y) / 2;
        if(z >= 5.0)
        {
            puts("Aluno aprovado.");
        }
        else 
        {
            puts("Aluno reprovado.");
        }
        printf("Media final: %.1lf", z); //必执行语句提到外面
    }
    
    return 0;
}

662. 点的坐标

给定两个保留一位小数的浮点数 X,Y，用来表示一个点的横纵坐标。

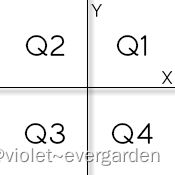
请你判断该点在坐标系中的位置。

输入格式
共一行，包含两个浮点数 X,Y，表示点的横纵坐标。

输出格式
如果点在第一象限，则输出 Q1，在第二象限，则输出 Q2，以此类推。

如果点在原点处，则输出 Origem。

否则，如果点在 x 坐标上，则输出 Eixo X，在 y 坐标上，则输出 Eixo Y。

数据范围
−10.0≤X,Y≤10.0
输入样例1：
4.5 -2.2
输出样例1：
Q4
输入样例2：
0.0 0.0
输出样例2：
Origem

犇版

#include 

using namespace std;

int main()
{
    double x,y;
    cin >> x >> y;

    if(x==0 && y==0) puts("Origem");//原点
    else if(x * y == 0) puts(x == 0 ? "Eixo Y" : "Eixo X"); //y或x为0
    else if(x > 0) puts(y > 0 ? "Q1" : "Q4"); // x > 0 
    else puts(y > 0 ? "Q2" : "Q3"); //x < 0
}

朴素


#include 
#include 

using namespace std;

int main()
{
    double x, y;
    cin >> x >> y;
    if (x == 0 && y == 0)
        puts("Origem");
    else if (y == 0)
        puts("Eixo X");
    else if (x == 0)
        puts("Eixo Y");
    else if (x > 0 && y > 0)
        puts("Q1");
    else if (x < 0 && y > 0)
        puts("Q2");
    else if (x < 0 && y < 0)
        puts("Q3");
    else
        puts("Q4");
    return 0;
}

663. 简单排序

读取三个整数并按升序对它们进行排序。

输入格式
共一行，包含三个整数。

输出格式
首先，将三个整数按升序顺序输出，每行输出一个整数。

然后，输出一个空行。

紧接着，将三个整数按原输入顺序输出，每行输出一个整数。

数据范围
−100≤输入整数≤100
输入样例：
7 21 -14
输出样例：
-14
7
21

7
21
-14

标准排版


#include
#include//sort
#include //memcpy

using namespace std;

const int N = 5;
int n = 3;
int a[N], b[N];

int main()
{
    for(int i = 0; i < n; i++) scanf("%d", &a[i]);
    memcpy(b, a, sizeof a);
    sort(a, a + n);
    
    for(int i = 0; i < n; i++) printf("%d\n", a[i]);   
    puts("");
    for(int i = 0; i < n; i++) printf("%d\n", b[i]);   
    return 0;
}

直接输出版


#include 
#include 
#include 

using namespace std;

int n = 3, a[3], b[3];

int main()
{
    for (int i = 0; i < n; i ++ )
        cin >> a[i];
    memcpy(b, a, sizeof a);
    sort(a, a + n);
    for (auto x: a)
        cout << x << endl;
    cout << endl;
    for (auto x: b)
        cout << x << endl;
    return 0;
}

快排版hh

#include
#include

using namespace std;

int a[3],tmp[3];

int cmp(int a,int b)
{
    return a < b;
}

void quick_sort(int q[],int l,int r) 
{
    if(l >= r) return ;//Memory Limit Exceeded   内存超限制 ,没加边界出口
    
    int x = q[l + r >> 1], i = l - 1 , j = r + 1;
    
    while(i < j)
    {
        do i ++ ; while(q[i] < x);
        do j -- ; while(q[j] > x);
        if(i < j) swap(q[i],q[j]);
    }
    
    quick_sort(q,l,j),quick_sort(q,j+1, r);
}

int main()
{
    for(int i = 0;i < 3;i++)
    {
        scanf("%d",&a[i]);
        tmp[i] = a[i];
    }
    
    quick_sort(a,0,2); //[首地址，结尾地址]
    //sort(a,a+3,cmp);
    
    for(int i = 0;i < 3;i++) printf("%d\n",a[i]);
    printf("\n");
    for(int i = 0;i < 3;i++) printf("%d\n",tmp[i]);
        
    return 0;
}

664. 三角形

读取三个浮点数 A，B 和 C 并验证是否可以用它们形成三角形。

如果可能，则计算并输出三角形的周长：

Perimetro = XX.X

如果不可能，则计算并输出以 A 和 B 为底以 C 为高的梯形面积：

Area = XX.X

输入格式
共一行，包含三个浮点数 A,B,C。

输出格式
按题目描述格式，输出答案，答案保留一位小数。

数据范围
0 输入样例1：
6.0 4.0 2.0
输出样例1：
Area = 10.0
输入样例2：
6.0 4.0 2.1
输出样例2：
Perimetro = 12.1

判断三边是否可构成三角形 : 两边之和>第三边两边之差的绝对值<第三边

#include
#include

using namespace std;
int main()
{
    double a,b,c;
    scanf("%lf%lf%lf", &a, &b, &c);
    //判断三边是否可构成三角形   两边之和>第三边 两边之差的绝对值<第三边
    if(a + b > c && fabs(a - b) < c) printf("Perimetro = %.1lf", a + b + c);
    else printf("Area = %.1lf",(a+b) * c / 2);
    return 0;
}

665. 倍数

读取两个正整数值 A 和 B。

如果其中一个是另一个的整数倍，则输出 Sao Multiplos，否则输出 Nao sao Multiplos。

输入格式
共一行，两个整数 A 和 B。

输出格式
按题目所述，输出结果。

数据范围
0 输入样例：
6 24
输出样例：
Sao Multiplos

#include

using namespace std;

int a,b;

int main()
{

    scanf("%d%d",&a,&b);
    if(a % b == 0 || b % a == 0)printf("Sao Multiplos");
    else printf("Nao sao Multiplos");

    return 0;
}

666. 三角形类型

读取表示三角形三条边的 3 个浮点数 A，B 和 C 并按降序排列，使 A 边是三边中最大的一边。

接下来，根据以下情况，确定它们可以组成的三角形类型：

如果 A≥B+C，则说明三条边不能构成三角形，请输出：NAO FORMA TRIANGULO
否则，说明三条边可以构成三角形，然后按如下情况输出：
如果A²=B²+C²，请输出：TRIANGULO RETANGULO
如果A²>B²+C²，请输出：TRIANGULO OBTUSANGULO
如果A²2+C²，请输出：TRIANGULO ACUTANGULO
如果三个边长度都相同，请输出：TRIANGULO EQUILATERO
如果只有两个边长度相同而第三个边长度不同，请输出：TRIANGULO ISOSCELES
输入格式
共一行，包含三个浮点数 A,B,C。

输出格式
输出 A,B,C 组成的三角形的类型。

注意，上述条件可能满足不止一条，这种情况下将所有类型名称，按题目介绍顺序输出，每行输出一条。

数据范围
0 输入样例：
7.0 5.0 7.0
输出样例：
TRIANGULO ACUTANGULO
TRIANGULO ISOSCELES

#include 
#include

using namespace std;

int main()
{
    double a, b, c;
    cin >> a >> b >> c;

    if (a < b) swap(a, b);
    if (a < c) swap(a, c);
    if (b < c) swap(b, c);

    if (a >= b + c) 
        cout << "NAO FORMA TRIANGULO" << endl;
    else
    {
        if (a * a == b * b + c * c) 
            cout << "TRIANGULO RETANGULO" << endl;
        if (a * a > b * b + c * c)
            cout << "TRIANGULO OBTUSANGULO" << endl;
        if (a * a < b * b + c * c) 
            cout << "TRIANGULO ACUTANGULO" << endl;
        if (a == b && a == c) 
            cout << "TRIANGULO EQUILATERO" << endl;
        if ((a == b && a != c && b != c) || (a == c && a != b && c != b) || (b == c && b != a && c != a)) 
            cout << "TRIANGULO ISOSCELES" << endl;
    }

    return 0;
}

667. 游戏时间

读取两个整数 A 和 B，表示游戏的开始时间和结束时间，以小时为单位。

然后请你计算游戏的持续时间，已知游戏可以在一天开始并在另一天结束，最长持续时间为 24 小时。

如果 A 与 B 相等，则视为持续了 24 小时。

输入格式
共一行，包含两个整数 A 和 B。

输出格式
输出格式为 O JOGO DUROU X HORA(S)，其中 X 为游戏持续时间。

数据范围
0≤A,B≤23
输入样例1：
16 2
输出样例1：
O JOGO DUROU 10 HORA(S)
输入样例2：
0 0
输出样例2：
O JOGO DUROU 24 HORA(S)
输入样例3：
2 16
输出样例3：
O JOGO DUROU 14 HORA(S)

(x + n % n) ：x映射在[0, n - 1]


#include 

using namespace std;

int main() {
    int A, B;
    scanf("%d%d", &A, &B);
    if (A >= B) B += 24;  //数学上负数 % 24的效果 
    printf("O JOGO DUROU %d HORA(S)\n", B - A);

    return 0;
}


#include
#include
using namespace std;
int main()
{
    int a,b;
    scanf("%d%d",&a,&b);
    
    if(a==b) printf("O JOGO DUROU 24 HORA(S)");
    else printf("O JOGO DUROU %d HORA(S)",abs(a-b)%24 ); 
    return 0;
}

668. 游戏时间

读取四个整数 A,B,C,D，用来表示游戏的开始时间和结束时间。

其中 A 和 B 为开始时刻的小时和分钟数，C 和 D 为结束时刻的小时和分钟数。

请你计算游戏的持续时间。

比赛最短持续 1 分钟，最长持续 24 小时。

输入格式
共一行，包含四个整数 A,B,C,D。

输出格式
输出格式为 O JOGO DUROU X HORA(S) E Y MINUTO(S)，表示游戏共持续了 X 小时 Y 分钟。

数据范围
0≤A,C≤23,
0≤B,D≤59
输入样例1：
7 8 9 10
输出样例1：
O JOGO DUROU 2 HORA(S) E 2 MINUTO(S)
输入样例2：
7 7 7 7
输出样例2：
O JOGO DUROU 24 HORA(S) E 0 MINUTO(S)
输入样例3：
7 10 8 9
输出样例3：
O JOGO DUROU 0 HORA(S) E 59 MINUTO(S)

y总

#include 

using namespace std;

int main()
{
    int a, b, c, d;
    cin >> a >> b >> c >> d;

    int tm = (c - a) * 60 + d - b;  //小时差值*60 + 分钟差值 == 总差值(分钟)
    if (tm <= 0) tm += 60 * 24; //说明时间跨度两天：

    int hours = tm / 60, minutes = tm % 60;
    printf("O JOGO DUROU %d HORA(S) E %d MINUTO(S)\n", hours, minutes);

    return 0;
}

取模映射
$类比散列表 :$ （x % N + N）% N

#include 
#include 

using namespace std;

int main()
{
    int a, b, c, d;
    cin >> a >> b >> c >> d;
    if (a == c && b == d) puts("O JOGO DUROU 24 HORA(S) E 0 MINUTO(S)"); //特判最长持续 24 小时
    else 
    {
        int m = c * 60 + d - a * 60 - b + 1440; //24 * 60 == 1440分钟   
        m %= 1440;//如果跨度为两天也会映射到1440：一天之内
        printf("O JOGO DUROU %d HORA(S) E %d MINUTO(S)\n", m / 60, m % 60);
    }
    return 0;
}

朴素写法
linminqingying

#include 

using namespace std;

int main()
{
    int a, b, c, d, minute1, minute2;

    cin >> a >> b >> c >> d;
    minute1 = a * 60 + b;
    minute2 = c * 60 + d;

    int hour = 0, minute = 0;
    int dec = minute2 - minute1;

    if(dec == 0)
    {
        hour = 24;
        minute = 0;
    }
    else
    {
        if(dec < 0)       //如 22:00 到 5:00 
        {      
            dec += 24 * 60; //dec计算的是5点到22点的时间，共17小时。故应用一天的分钟(24*60)减去，才是正确经历的分钟
        }
        hour = dec / 60;
        minute = dec % 60;
    }
    cout << "O JOGO DUROU " << hour << " HORA(S) E " << minute << " MINUTO(S)";
    return 0;
}

669. 加薪

ABC 公司决定给员工加薪，加薪情况如下所示：

薪水	涨薪幅度
0 - 400.00	15%
400.01 - 800.00	12%
800.01 - 1200.00	10%
1200.01 - 2000.00	7%
超过 2000.00	4%

读取员工的工资，计算并输出员工的新工资，以及员工增加的收入和涨薪幅度。

输入格式
共一行，包含一个保留两位小数的浮点数。

输出格式
输出格式如下所示：

第一行输出 Novo salario: X，X 表示员工新工资，保留两位小数。

第二行输出 Reajuste ganho: Y，Y 表示员工增加的具体收入数值，保留两位小数。

第三行输出 Em percentual: Z，Z 表示涨薪幅度，注意用百分比表示。

数据范围
0≤原工资≤2500.00
输入样例：
400.00
输出样例：
Novo salario: 460.00
Reajuste ganho: 60.00
Em percentual: 15 %

#include

using namespace std;

double a[5]={0,400.00,800.00,1200.00,2000.00};
double b[5]={0.15,0.12,0.10,0.07,0.04};
double x;
double ans,sum;
int res;
int main()
{
    cin>>x;
    if(x<=a[4])
    {
        for(int i = 0;i < 5; i++) //O(5)还好
        {
            if(i != 4 && x > a[i] && x <= a[i + 1]) 
            {
                sum = x * b[i];
                ans = x + sum;
                res = b[i] * 100;
            }
        }
    }
    else
    {
        sum = x * b[4];
        ans = x + sum;
        res = b[4] * 100;
    }
    printf("Novo salario: %.2lf\n", ans);
    printf("Reajuste ganho: %.2lf\n", sum);
    printf("Em percentual: %d %\n", res);
    return 0;
}

/*被佬打败：佬の代码
#include

using namespace std;

double a;
int main()
{
    cin>>a;
    cout << fixed << setprecision(2);
    double add = 0;
    if(a >= 0 && a <= 400) add = a * 0.15;
    else if(a <= 800) add = a * 0.12;
    else if(a <= 1200) add= a * 0.1;
    else if(a <= 2000) add = a * 0.07;
    else add = a * 0.04;
    cout<<"Novo salario: "<=0&&a<=400) cout<<"15 %";
    else if(a<=800) cout<<"12 %";
    else if(a<=1200) cout<<"10 %";
    else if(a<=2000) cout<<"7 %";
    else cout<<"4 %";
}
*/

670. 动物

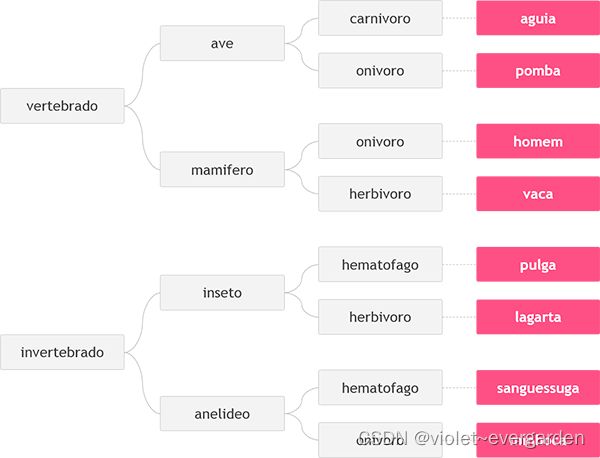
给定你三个葡萄牙语单词，这些词将根据下表从左到右定义一个动物。

请你确定并输出这个动物的名称。

输入格式
根据上表，输入包含三个单词，每行一个，用以识别动物，单词由小写字母构成。

输出格式
输出识别出的动物的名称。

输入样例：
vertebrado
mamifero
onivoro
输出样例：
homem


#include 
#include

using namespace std;  //【仅需判断每个单词的前几个不同字母，能区分即可】

int main()
{
    string a[3];
    string ss;
    for(int i = 0; i < 3; i++) cin >> a[i],ss += a[i][0];


    if(ss=="vac") cout<<"aguia";
    if(ss=="vao") cout<<"pomba";
    if(ss=="vmo") cout<<"homem";
    if(ss=="vmh") cout<<"vaca";
    if(ss=="iih") // 情况特殊
    {
        if(a[2] == "hematofago") cout<<"pulga";
        else cout<<"lagarta";
    }
    if(ss=="iah") cout<<"sanguessuga";
    if(ss=="iao") cout<<"minhoca";

}

yxc

#include 

using namespace std;

int main()
{
    string a, b, c;
    cin >> a >> b >> c;

    if (a == "vertebrado")
    {
        if (b == "ave")
        {
            if (c == "carnivoro") cout << "aguia" << endl;
            else cout << "pomba" << endl;
        }
        else
        {
            if (c == "onivoro") cout << "homem" << endl;
            else cout << "vaca" << endl;
        }
    }
    else
    {
        if (b == "inseto")
        {
            if (c == "hematofago") cout << "pulga" << endl;
            else cout << "lagarta" << endl;
        }
        else
        {
            if (c == "hematofago") cout << "sanguessuga" << endl;
            else cout << "minhoca" << endl;
        }
    }

    return 0;
}

671. DDD

给定一个整数，请根据下表确定并输出其对应的城市名称：

如果输入数字不在上表中，则输出 DDD nao cadastrado。

输入格式
共一行，包含一个整数。

输出格式
输出对应城市名称，如果没有对应城市名称，则输出 DDD nao cadastrado。

输入样例：
11
输出样例：
Sao Paulo

#include 

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);

    if (n == 61) printf("Brasilia");
    else if (n == 71) printf("Salvador");
    else if (n == 11) printf("Sao Paulo");
    else if (n == 21) printf("Rio de Janeiro");
    else if (n == 32) printf("Juiz de Fora");
    else if (n == 19) printf("Campinas");
    else if (n == 27) printf("Vitoria");
    else if (n == 31) printf("Belo Horizonte");
    else printf("DDD nao cadastrado");

    return 0;
}

old_code

#include 
#include 

using namespace std;

int main() {

    int DDD[] = {61, 71, 11, 21, 32, 19, 27, 31};
    string Destination[] = {"Brasilia", "Salvador", "Sao Paulo", "Rio de Janeiro", "Juiz de Fora", "Campinas", "Vitoria", "Belo Horizonte"};
    int n;

    cin >> n;
    
    for(int i = 0; i < 8; i++) {
        if(n == DDD[i]) {
            cout << Destination[i];
            break;
        } else if(i == 7) {  
            cout << "DDD nao cadastrado";
        }
    } 

    return 0;

}

672. 税

读取一个保留两位小数的浮点数值，表示一个公民的工资。

在公民缴纳个人所得税时，不同收入部分需要缴税的税率也是不同的。

请根据下表确定该公民需要缴纳的个人所得税是多少。

输入格式
共一行，包含一个浮点数。

输出格式
如果公民需要缴税，则输出所需缴纳的税额。输出格式为 R$ X，其中 X 为个税的金额，保留两位小数。

如果公民不需要缴税，则输出 Isento。

数据范围
0≤公民工资≤5000
输入样例1：
3002.00
输出样例1：
R$ 80.36
输入样例2：
1700.00
输出样例2：
Isento
输入样例3：
4520.00
输出样例3：
R$ 355.60
样例解释
对于样例 1，0∼2000.00 部分不用缴税，2000.01∼3000.00 部分按 8% 的税率缴税，共计 1000×8%=80，3000.01∼3002.00 部分按 18% 的税率缴税，共计 2×18%=0.36，合计 80.36。

对于样例 2，公民收入未超过 2000，所以输出 Isento。

对于样例 3，0∼2000.00 部分不用缴税，2000.01∼3000.00 部分按 8% 的税率缴税，共计 1000×8%=80，3000.01∼4500.00 部分按 18% 的税率缴税，共计 1500×18%=270，4500.01∼4520 部分按 28% 的税率缴税，共计 20×28%=5.60，合计 355.60。

水电费阶梯收费

#include
#include

using namespace std;

int main()
{
    double n;//cin比较简单
    scanf("%lf", &n);//没有对应%lf则没有读入, 为0
    if(n > 0 && n <= 2000.0) printf("Isento"); 
    else if(n > 2000.0 && n <= 3000) printf("R$ %.2lf", (n - 2000) * 0.08);
    else if(n > 3000.0 && n <= 4500) printf("R$ %.2lf", (n - 3000) * 0.18 + 80);//加上前面低阶部分已确定的价值 
    else if(n > 4500.0) printf("R$ %.2lf", (n - 4500) * 0.28 + 350);
    return 0;
}

3.循环语句

708. 偶数

编写一个程序，输出 1 到 100 之间（包括 1 和 100）的全部偶数。

输入格式
无输入。

输出格式
输出全部偶数，每个偶数占一行。

输入样例
No input
输出样例
2
4
6
…
100

#include

using namespace std;

int main()
{
    for(int i = 2;i <= 100 ;i += 2)  printf("%d\n",i);

    return 0;
}

709. 奇数

输入一个整数 X，输出 1 到 X 之间（包括 1 和 X）的全部奇数。

输入格式
一个整数 X。

输出格式
输出所有满足条件的奇数，每个数占一行。

数据范围
1≤X≤1000
输入样例：
8
输出样例：
1
3
5
7

#include

using namespace std;

int n;

int main()
{
    scanf("%d%d",&n);
    
    for(int i = 1;i <= n;i += 2) printf("%d\n",i);
   
    return 0;
}

710. 六个奇数

读取一个整数 X，输出 X 之后的 6 个奇数，如果 X 也是奇数，那么它也算作 6 个奇数之一。

输入格式
一个整数 X。

输出格式
所有满足条件的奇数，每个占一行。

数据范围
1≤X≤100
输入样例：
9
输出样例：
9
11
13
15
17
19

//从x开始(包括x)找6个相邻奇数
#include

using namespace std;

int x, cnt;

int main()
{
    scanf("%d",&x);

    for(int i = x; cnt < 6; i++)
    {
        if(i % 2)
        {
            printf("%d\n", i);
            cnt++;
        }
    }

    return 0;
}

711. 乘法表

输入一个整数 N，输出 N 的乘法表，如下：

1 x N = N
2 x N = 2N
…
10 x N = 10N
输入格式
一个整数 N。

输出格式
输出 N 的乘法表，具体形式参照输出样例。

数据范围
1 输入样例：
140
输出样例：
1 x 140 = 140
2 x 140 = 280
3 x 140 = 420
4 x 140 = 560
5 x 140 = 700
6 x 140 = 840
7 x 140 = 980
8 x 140 = 1120
9 x 140 = 1260
10 x 140 = 1400

#include

using namespace std;

int n;
int main()
{
    scanf("%d",&n);

    for(int i = 1;i <= 10;i ++)
        printf("%d x %d = %d\n", i, n, i * n);

    return 0;
}

712. 正数

输入 6 个实数，它们要么是正数，要么是负数。

请你统计并输出正数的个数。

输入格式
六个数字，每个占一行。

输出格式
输出格式为 x positive numbers，其中 x 为正数的个数。

数据范围
输入数字的绝对值不超过 100。

输入样例：
7
-5
6
-3.4
4.6
12
输出样例：
4 positive numbers

#include

using namespace std;

int cnt;
double n;  //number[i]没必要
int main()
{
    for(int i = 0; i < 6; i++)
    {
      scanf("%lf", &n);  
      if(n > 0.0) cnt ++ ;  //或者(double)0
    }

    printf("%d positive numbers",cnt);

    return 0;
}

713. 区间

读取 N 个整数 X1,X2,…,XN，判断这 N 个整数中有多少个在 [10,20] 的范围内，有多少个在范围外。

输入格式
第一行包含整数 N，表示共有 N 个整数需要进行判断。

接下来 N 行，每行包含一个整数 Xi。

输出格式
第一行输出 x in，其中 x 为在范围内的整数的数量。

第二行输出 y out，其中 y 为在范围外的整数的数量。

数据范围
1≤N≤10000,
−107 输入样例：
4
14
123
10
-25
输出样例：
2 in
2 out

#include

using namespace std;

int n,x,t,tmp;

int main()
{

    scanf("%d",&n); tmp = n; //n值修改,但n仍需使用,先存下来

    while(n --)//n值修改 （或者tmp --）
    {
        scanf("%d",&t);
        if(10 <= t && t <= 20) x ++; //在[10,20]内的个数为x , 区间外的数量为y
    }
    //y = tmp - x;        
    printf("%d in\n%d out", x, tmp - x);

    return 0;
}

714. 连续奇数的和

给定两个整数 X 和 Y，输出在他们之间（不包括 X 和 Y）的所有奇数的和。

输入格式
第一行输入 X，第二行输入 Y。

输出格式
输出一个整数，表示所有满足条件的奇数的和。

数据范围
−100≤X,Y≤100
输入样例1：
6
-5
输出样例1：
5
输入样例2：
15
12
输出样例2：
13
输入样例3：
12
12
输出样例3：
0

#include

using namespace std;

int x, y, sum;

int main()
{
    scanf("%d%d", &x, &y);
    if(x > y) swap(x,y); //读入后判断
    for(int i = x + 1; i < y ; i++)  //区间(x,y)遍历
        if(i % 2) sum += i;     //  x % n 取值范围 [-n + 1 , n - 1]

    printf("%d", sum);

    return 0;
}

715. 余数

输入一个整数 N，请按顺序输出 1 到 10000 之间（不包括 1 和 10000）的所有除以 N 余 2 的数字。

输入格式
一个整数 N。

输出格式
输出所有满足条件的数字，从小到大每行输出一个。

数据范围
2 输入样例：
13
输出样例：
2
15
28
41
…

#include

using namespace std;

int n;
int main()
{
    scanf("%d",&n);

    for(int i = 2; i < 10000; i++)
        if(i % n == 2)
            printf("%d\n", i);

    return 0;
}

716. 最大数和它的位置

给定 100 个整数，请你找出其中最大的数字，以及它的输入位置（位置从 1 开始）。

输入格式
共 100 行，每行包含一个整数。

输出格式
第一行输出最大的数字。

第二行输出该数字的输入位置。

数据范围
1≤输入数字≤50000,
保证输入数字互不相同。

输入样例：
22229
48558
24992
4755
11923
…
20213
输出样例：
48558
2

#include 

using namespace std;

int main()
{
    int maxv = 0, idx, n;
    for(int i = 1; i <= 100; i++) //下标从1开始
    {
        scanf("%d", &n);
        if(n > maxv)
        {
            maxv = n;
            idx = i;
        }
    }
    printf("%d\n%d", maxv, idx);

    return 0;
}

#include 

using namespace std;

int main(){
    int x = 0, y, a;
    for(int i = 1;i <= 100;i++){
        cin >> a;
        if(a > x){
            x = a;
            y = i;
        }
    }
    cout << x << endl << y;
    return 0;
}

717. 简单斐波那契

以下数列 0 1 1 2 3 5 8 13 21 … 被称为斐波纳契数列。

这个数列从第 3 项开始，每一项都等于前两项之和。

输入一个整数 N，请你输出这个序列的前 N 项。

输入格式
一个整数 N。

输出格式
在一行中输出斐波那契数列的前 N 项，数字之间用空格隔开。

数据范围
0 输入样例：
5
输出样例：
0 1 1 2 3

朴素版-递推和递归

#include

using namespace std;

const int N = 50;
int n;
int f[N];// 不超过int最多f[46]

//递推
void init_Fib() //题目：下标从0开始为第一项
{
    int a = 0, b = 1, c;
    f[0] = 0, f[1] = 1;
    for(int i = 2; i <= 46; i++)
    {
        c = a + b;
        a = b, b = c;
        f[i] = c;
    }
        
}

int main()
{
    scanf("%d",&n);
    // f[0] = 0, f[1] = 1;
    // for(int i = 2;i < n;i++) f[i] = f[i - 1] + f[i - 2];   
    // for(int i = 0;i < n;i++) printf("%d ",f[i]);
    init_Fib();
    for(int i = 0;i < n;i++) printf("%d ",f[i]);
        
    return 0;
}

不开数组版


#include

int n;
int a, b = 1, c;

int main()
{
    scanf("%d",&n);
    while(n--)
    {
        printf("%d ",a); //每次计算完，a位置已确定 【第一项从a开始, a每轮后移一项】
        c = a + b;
        a = b, b = c;
    }
}


//附赠高精度版
/*
#include
#include
#pragma GCC optimize(3)
#define M 100001
int n,a[M],b[M],c[M],la=1,lb=1;
void add(){
    memcpy(c,b,sizeof(b));
    la=lb;
    for(int i=1;i<=lb;i++){
        b[i]+=a[i];
        if(b[i]>9&&i9) b[lb]-=10,b[++lb]++;
    memcpy(a,c,sizeof(c));
}
int main(){
    scanf("%d",&n),b[1]=1;
    while(n--){
        for(int i=la;i;i--) printf("%d",a[i]);
        printf(" ");
        add();
    }
}

718. 实验

医学部一共进行了 N 场动物实验。

共有三种小动物可用来实验，分别是青蛙、老鼠和兔子。

每次实验都会选取其中一种动物来参与实验，选取数量若干。

现在请你统计一下医学部一共用了多少小动物，每种分别用了多少，每种动物使用数量占总量的百分比分别是多少。

输入格式
第一行包含整数 N，表示实验次数。

接下来 N 行，每行包含一个整数 A（表示一次实验使用的小动物的数量）和一个字符 T（表示一次实验使用的小动物的类型，C 表示兔子(coney)，R 表示老鼠(rat)，F 表示青蛙(frog)）。

输出格式
请你参照输出样例，输出所用动物总数，每种动物的数量，以及每种动物所占百分比。

注意输出百分比时，保留两位小数。

数据范围
1≤N≤100,
1≤A≤15
输入样例：
10
10 C
6 R
15 F
5 C
14 R
9 C
6 R
8 F
5 C
14 R
输出样例：
Total: 92 animals
Total coneys: 29
Total rats: 40
Total frogs: 23
Percentage of coneys: 31.52 %
Percentage of rats: 43.48 %
Percentage of frogs: 25.00 %

y总简版

#include 
#include 
#include 

using namespace std;

int main()
{
    int sc = 0, sr = 0 , sf = 0, total = 0;
    int n;
    cin >> n;
    while (n -- )
    {
        int a;
        char c;
        scanf("%d %c", &a, &c);//scanf %d %c 中间空格才读入正确 !!!
        if (c == 'C') sc += a; //简单分支
        else if (c == 'R') sr += a;
        else sf += a;
        total += a; //总和
    }
   
    printf("Total: %d animals\n", total);
    printf("Total coneys: %d\n", sc);
    printf("Total rats: %d\n", sr);
    printf("Total frogs: %d\n", sf);
    printf("Percentage of coneys: %.2lf %\n", sc * 100.0 / total);
    printf("Percentage of rats: %.2lf %\n", sr * 100.0 / total);
    printf("Percentage of frogs: %.2lf %\n", sf * 100.0 / total);

    return 0;
}

加了数组存-化繁了-简单分支就行

#include

using namespace std;

int num,x,sum;
char c;
int n[3]; //C,R,F --  1 2 3 
int main()
{
    scanf("%d",&num);
    
    while(num--)
    {
        scanf("%d %c",&x,&c);//scanf %d %c 中间空格才读入正确
        //cout << x <<"  " <<  c << endl;
        if(c == 'C') n[0] += x;
        else if(c == 'R') n[1] += x;
        else n[2] += x;
    }
    sum = n[0] + n[1] + n[2];
    
    cout <<"Total: "<< sum <<" animals"<< endl;
    cout <<"Total coneys: "<< n[0] << endl;
    cout <<"Total rats: "<< n[1] << endl;
    cout <<"Total frogs: "<< n[2] << endl;
    printf("Percentage of coneys: %.2lf %\n", (double)n[0] / sum * 100);
    printf("Percentage of rats: %.2lf %\n", (double)n[1] / sum * 100);
    printf("Percentage of frogs: %.2lf %\n", (double)n[2] / sum * 100);
    
    return 0;
}

719. 连续奇数的和

输入 N 对整数对 X,Y，对于每对 X,Y，请你求出它们之间（不包括 X 和 Y）的所有奇数的和。

输入格式
第一行输入整数 N，表示共有 N 对测试数据。

接下来 N 行，每行输入一组整数 X 和 Y。

输出格式
每对 X,Y 输出一个占一行的奇数和。

数据范围
1≤N≤100,
−1000≤X,Y≤1000
输入样例：
7
4 5
13 10
6 4
3 3
3 5
3 4
3 8
输出样例：
0
11
5
0
0
0
12

#include
#include

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);
    int x, y;
    while (n -- )
    {
        int sum = 0;
        scanf("%d%d", &x, &y);
        if(x > y) swap(x, y); //注意题目没有规定x <= y
        for(int i = x + 1; i < y; i++)
            if(i & 1) sum += i; //或if(i % 2)
        printf("%d\n", sum);
    }
    
    return 0;
}

#include
int x,y,ans,t;
int main(){
    scanf("%d",&t);
    while(t--){
        ans=0;
        scanf("%d%d",&x,&y);
        for(int i=(x<y?x:y)+1;i<(x>y?x:y);i++) if(i&1) ans+=i;
        printf("%d\n",ans);
    }
}

720. 连续整数相加

读入两个整数值 A 和 N，计算从 A 开始的 N 个连续整数的和。

注意，如果读入的 N 为 0 或负数，则继续读取数字直至读入 N 值为正整数为止。

输入格式
共一行，包含整数 A 和若干个整数 N（不超过 100 个）。

输出格式
一个整数，表示从 A 开始的 N 个连续整数的和。

数据范围
1≤A≤100,
−100≤N≤100
输入样例1：
3 2
输出样例1：
7
输入样例2：
3 -1 0 -2 2
输出样例2：
7

读入处理

#include

using namespace std;

int main()
{
    int A;
    scanf("%d", &A);
    int n;
    while(scanf("%d", &n))
        if(n > 0) break; //读到n为正数
    
    int sum = 0;
    for(int i = A; i < A + n; i++)
        sum += i;
    printf("%d", sum);
    
    return 0;
}

高斯

#include
using namespace std;
int main()
{
    int a,n;
    scanf("%d",&a);
    while(scanf("%d",&n) && n<=0); //while(scanf("%d",&n),n<=0);也可逗号表达式，连接多个表达式组成一个更大的表达式

    printf("%d",(a + a+n-1) * n / 2); //(a~a+n的和) :【高斯5050】：(首项 + 末项) * 总项数/2(即对数)    
    return 0;
}

721. 递增序列

读取一系列的整数 X，对于每个 X，输出一个 1,2,…,X 的序列。

输入格式
输入文件中包含若干个整数，其中最后一个为 0，其他的均为正整数。

每个整数占一行。

对于输入的正整数，按题目要求作输出处理。

对于最后一行的整数 0，不作任何处理。

输出格式
对于每个输入的正整数 X，输出一个从 1 到 X 的递增序列，每个序列占一行。

数据范围
1≤X≤100
输入样例：
5
10
3
0
输出样例：
1 2 3 4 5
1 2 3 4 5 6 7 8 9 10
1 2 3

while(scanf(“%d”,&n))会一直读到文件末尾
而题目中读到0就要停止,相当于多读了一行【加上n!=0判断即可】

#include

using namespace std;

int n;

int main()
{
    while(scanf("%d",&n), n) //逗号取最后一个表达式的值停止   : 也可以while(scanf("%d", &n) && n)
    {
        for(int i = 1;i <= n;i++) printf("%d ",i);
        puts("");
    }
    return 0;
}

722. 数字序列和它的和

输入若干个整数对 M,N，对于每个数对，输出以这两个数为最大值和最小值的公差为 1 的等差数列。

注意，当输入整数对中，任意一个数为 0 或负整数时，立即停止输入，且该组数对无需作任何处理。

输入格式
输入共若干行，每行包含两个整数。

最后一行的两个整数中，至少有一个是非正整数。

输出格式
对于每组需作处理的数对，输出一个结果，每个结果占一行。

结果包含从最小值到最大值的数字序列以及数字序列各数字之和。

具体格式请参照输出样例。

数据范围
M,N≤100
输入样例：
2 5
6 3
5 0
输出样例：
2 3 4 5 Sum=14
3 4 5 6 Sum=18

#include
#include

using namespace std;

int a,b,sum;

int main()
{
    
    //while(scanf("%d%d",&a,&b) && a > 0  &&  b > 0 )  //结束条件：最后一行的两个整数中，至少有一个是非正整数。--a或b有一个<=0结束
    while(scanf("%d%d", &a, &b) , a > 0 && b > 0)
    {                                                               //推出执行条件 a > 0  &&  b > 0 
        if(a > b) swap(a,b);//题目没有规定 a <= b 需判断
        for(int i = a;i <= b;i++) 
        {
            printf("%d ",i);
            sum += i;
        }
        printf("Sum=%d\n",sum);
        sum = 0;
    }
    return 0;
}

723. PUM

输入两个整数 N 和 M，构造一个 N 行 M 列的数字矩阵，矩阵中的数字从第一行到最后一行，按从左到右的顺序依次为 1,2,3,…,N×M。

矩阵构造完成后，将每行的最后一个数字变为 PUM。

输出最终矩阵。

输入格式
共一行，包含两个整数 N 和 M。

输出格式
输出最终矩阵，具体形式参照输出样例。

数据范围
1≤N,M≤20
输入样例：
7 4
输出样例：
1 2 3 PUM
5 6 7 PUM
9 10 11 PUM
13 14 15 PUM
17 18 19 PUM
21 22 23 PUM
25 26 27 PUM

#include

using namespace std;    

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n * m ; i++) //蛇形矩阵式枚举
    {
        if(i % m == 0) puts("PUM");
        else  printf("%d ", i);
    }
    return 0;
}

c++

//输出变量j是遍历共1到n*m的数，当j的值是列数（m）的倍数时输出PUM并换行，其他情况输出j的值和空格。
#include
using namespace std;    //看成一维，a%m == 0 cout <

int main()
{
    int n,m;
    cin>>n>>m;
    for(int j=1;j<=n*m;j++)
    {
        if(j%m==0)
            cout<<"PUM"<<endl;
        else
            cout<<j<<" ";
    }

    return 0;
}

724. 约数

输入一个整数 N，按照从小到大的顺序输出它的全部约数。

输入格式
一个整数 N。

输出格式
输出全部约数，每个约数占一行。

数据范围
1≤N≤1000
输入样例：
6
输出样例：
1
2
3
6

STL容器遍历方法
以vector可变长数组举例：

①【使用容器-配套for(auto x: 首地址) 遍历】 注意这时不能用vector res[N]指定长度
②vector< int > res , int len = res.size() 用res[i]
③for(vector< int >::iterator it = res.begin() ; it != res.end(); it++) printf("%d, *it); 【迭代器类比指针】

数论 [如果 n % b == 0 , 则 n % (n / b) == 0]

#include
#include
#include

using namespace std;

const int N = 1010;

int main()
{
    int n;
    scanf("%d", &n);
    vector<int> res;
    for(int i = 1; i <= n / i ; i++)   //枚举到sqrt（n） ，这样写是为了体现成对出现的约数  可以改成i * i <= n 
    		if(n % i == 0) //是约数   ，同时 n/i 也是约数
    		{
    			res.push_back(i); //放入 
    			if(i != n / i) res.push_back(n / i);	 // 平方相等时，i 与 n/i 两个约数一样，不要重复放
    		}	
	sort(res.begin(),res.end());    
	
	//四种遍历方式   
// 	int len = res.size();
// 	for(int i = 0; i < len; i++) printf("%d\n", res[i]);  
	for(auto i: res) printf("%d\n", i);
	
	//【使用容器-配套for(auto x: 首地址) 遍历】


    return 0;
}

暴力

#include

using namespace std;

int a;

int main()
{
    scanf("%d" ,&n);
    for(int i = 1; i <= n; i++)
        if(n % i == 0) printf("%d\n", i);
                
    return 0;
}

725. 完全数

一个整数，除了本身以外的其他所有约数的和如果等于该数，那么我们就称这个整数为完全数。

例如，6 就是一个完全数，因为它的除了本身以外的其他约数的和为 1+2+3=6。

现在，给定你 N 个整数，请你依次判断这些数是否是完全数。

输入格式
第一行包含整数 N，表示共有 N 个测试用例。

接下来 N 行，每行包含一个需要你进行判断的整数 X。

输出格式
每个测试用例输出一个结果，每个结果占一行。

如果测试数据是完全数，则输出 X is perfect，其中 X 是测试数据。

如果测试数据不是完全数，则输出 X is not perfect，其中 X 是测试数据。

数据范围
1≤N≤100,
1≤X≤10⁸
输入样例：
3
6
5
28
输出样例：
6 is perfect
5 is not perfect
28 is perfect

数论-枚举因数 O(nlogn)
n % i == 0,则n % (n / i) == 0 成对判断不重复就加入

#include

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);
    
    int x;
    int sum;
    while (n -- )
    {
        sum = 0; //[【清零】   编写好习惯:用tmp 意识到临时需清零
        scanf("%d", &x);
        for(int i = 1; i <= x / i; i++)  //(nlogn)
        {
            if(x % i == 0)
            {
                sum += i;//, printf("%d\n", i);
                if(i != x / i) sum += x / i;//, printf("%d\n", x / i); //成对判断
            }
        } 
        if(sum - x == x) printf("%d is perfect\n", x);  //x <= 1e8不会爆int   完全数定义：[不包括本身的所有因数 == 自身]     
        else printf("%d is not perfect\n", x);
    }
    
    return 0;
}

数学吊打c++系列
100000000 内的完全数有且仅有 6,28,496,8128,335503366,28,496,8128,33550336 这五个.
根据上述内容, 这道题可以直接 O(1)解决.
完全数比较重要的几个性质
所有完全数都是三角形数
目前截止发现的所有完全数都以 6 或28 结尾
到现在为止,数学家们一共发现了 48 个完全数,且 48 个完全数全部是偶数
如果有人们没有找到的奇完全数,则它一定可以写成 12p+1 或 36p+9 的形式,而且 p 是素数
奇完全数一定大于 10300
完全数的约数的倒数之和为调和数
完全数可以表示成连续奇数的立方和
完全数可以表示成 22 的连续自然数的次幂之和,且这些自然数的数量必定是素数
完全数计算法
若 2p−1 是素数(亦称其为梅森素数),则 2p−1∗(2p−1) 是完全数.

#include 

using namespace std;

int main() {
    int tt;
    cin >> tt;
    while (tt--) {
        int n;
        cin >> n;
        if (n == 6 || n == 28 || n == 496 || n == 8128 || n == 33550336)  
            cout << n << " is perfect" << endl;
        else cout << n << " is not perfect" << endl;
    }

    return 0;
}

726. 质数

一个大于 1 的自然数，如果除了 1 和它自身外，不能被其他自然数整除则称该数为质数。

例如 7 就是一个质数，因为它只能被 1 和 7 整除。

现在，给定你 N 个大于 1 的自然数，请你依次判断这些数是否是质数。

输入格式
第一行包含整数 N，表示共有 N 个测试数据。

接下来 N 行，每行包含一个自然数 X。

输出格式
每个测试用例输出一个结果，每个结果占一行。

如果测试数据是质数，则输出 X is prime，其中 X 是测试数据。

如果测试数据不是质数，则输出 X is not prime，其中 X 是测试数据。

数据范围
1≤N≤100,
1 输入样例：
3
8
51
7
输出样例：
8 is not prime
51 is not prime
7 is prime

此题限制O(n)

#include

using namespace std;

bool is_prime(int x)
{
    if(x < 2) return false;
    for(int i = 2; i <= x / i; i++) //枚举	i∈[ 2, x / i ]
        if(x % i == 0) return false;
    return true;
}

int main()
{
    int n;
    scanf("%d", &n);
    while (n -- )
    {
        int x;
        scanf("%d", &x);
        if(is_prime(x)) printf("%d is prime\n", x);
        else printf("%d is not prime\n", x);
    }
    return 0;
}

727. 菱形 [曼哈顿距离]

输入一个奇数 n，输出一个由 * 构成的 n 阶实心菱形。

输入格式
一个奇数 n。

输出格式
输出一个由 * 构成的 n 阶实心菱形。

具体格式参照输出样例。

数据范围
1≤n≤99
输入样例：
5

输出样例：
  *  
 *** 
*****
 *** 
  *

①曼哈顿距离 [观察能否使用] 【此题为斜正方形,有中心对称点】
公式: $d = ∣ x 1 - x 2∣ + ∣ y 1 - y 2∣$
②找与边界等距中心点
计算边界到中心点的曼哈顿距离d ：所有点与中心点的距离 <= d
此题：abs(中心点x - i) + abs(中心点y - j) <= n / 2 = d


#include 
#include 

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);

    int x = n / 2, y = n / 2;//①找与边界等距中心点

    for (int i = 0; i < n ; i ++ ) //判断每行
    {
        for (int j = 0; j < n; j ++ ) //每行第j列个元素
        {   //[正方形边界到中心点]的曼哈顿距离等于 n / 2 ：[在此范围内的点为'*',其余为空格]
            if ( abs(x - i) + abs(y - j) <= n / 2 ) printf("*");  
            else printf(" ");
        }
        puts("");
    }

    return 0;
}

区间枚举[-x,x] + abs()


#include 
#include 

using namespace std;

int n;

int main()
{
    scanf("%d" , &n);
    //②上下三角形合并，直接出菱形
    int x = n / 2;
    for (int i = -x; i <= x; i ++ )// 注意：[-x ~ x]  ==> 【绝对值从大到小, 再从小到大 ：对应前导空格数量先减后增！】
    {   //每行
        for (int j = 0; j < abs(i); j ++ ) printf(" ");//空格数量：先减后增
        for (int j = 0; j < n - abs(i) * 2; j ++ ) printf("*");//*与行号的关系：前半段、后半段
        puts("");
    }
    
    return 0;
}

(最菜法hh)
分段：去找行号和空格&星号的关系,输出上下三角形

#include 
#include 

using namespace std;

int n;

int main()
{
    scanf("%d" , &n);
    
    int x = n / 2;
    
    for (int i = 0; i < x; i ++)
    {
        for (int j = 0; j < x - i; j ++ ) cout <<' ';
        for (int j = 0; j < 2 * i + 1; j ++  ) cout << '*';
        puts("");
    }
    
    for (int i = 0; i < n - x; i ++ )                     
    {
        for (int j = 0; j < i; j ++ ) cout << ' ';
        for (int j = 0; j < n - 2 * i; j ++ ) cout << '*';
        puts("");
    }
    
    return 0;
}

scanf输入

如果“%d\n%c”的话，字符读入的将是空格。所以要用“\n”注释掉
【简单归纳输入格式怎么样，就读入操作成对应的样子】 //输入有换行就打\n
scanf(“%d\n%c”,&L,&c);
非正整数 <= 0

4.数组

737. 数组替换

输入一个长度为 10 的整数数组 X[10]，将里面的非正整数全部替换为 1，输出替换完成后的数组。

输入格式
输入包含 10 个整数，每个整数占一行。

输出格式
输出新数组中的所有元素，每个元素占一行。

输出格式为 X[i] = x，其中 i 为元素编号（从 0 开始），x 为元素的值。

数据范围
−100≤X[i]≤100
输入样例：
10
-9
0
-4
-10
0
-2
-7
7
4
输出样例：
X[0] = 10
X[1] = 1
X[2] = 1
X[3] = 1
X[4] = 1
X[5] = 1
X[6] = 1
X[7] = 1
X[8] = 7
X[9] = 4

简单判断

#include

using namespace std;

const int N = 12;

int x, a[N];

int main()
{
    for(int i = 0;i < 10;i++)
    {
        scanf("%d", &x);
        if(x <= 0) a[i] = 1;//非正整数
        else a[i] = x;
    }
    for(int i = 0;i < 10;i++) printf("X[%d] = %d\n", i, a[i]);
        
    return 0;
}

条件表达式-压缩代码

#include 
#include 
using namespace std;
int main(){
    for(int i = 0; i < 10; i ++ ){
        int x;  cin >> x;
        printf("X[%d] = %d\n", i, x <= 0 ? 1 : x);
    }
    return 0;
}

738. 数组填充

输入一个整数 V，输出一个长度为 10 的数组 N，数组中的第一个元素为 V，每个后续元素的值都为上一个元素的值的 2 倍。

例如，如果输入整数为 1，则数组为：1,2,4,8…
输入格式
输入一个整数 V。

输出格式
输出数组中的所有元素，每个元素占一行。

输出格式为 N[i] = x，其中 i 为元素编号（从 0 开始），x 为元素的值。

数据范围
1≤V≤50
输入样例：
1
输出样例：
N[0] = 1
N[1] = 2
N[2] = 4
N[3] = 8
N[4] = 16
N[5] = 32
N[6] = 64
N[7] = 128
N[8] = 256
N[9] = 512

#include

using namespace std;

typedef long long int LLD;

LLD a[11], v;

int main()
{


    scanf("%lld", &v); //%lld
    for(int i = 0;i < 10;i++)
    {
        a[i] = v;
        v <<= 1; // v *= 2; 
    }

    for(int i = 0;i < 10; i++) printf("N[%d] = %lld\n", i, a[i]);

    return 0;
}

739. 数组选择

输入一个长度为 100 的数组 A，请你按顺序输出其中不大于 10 的所有元素。

输入格式
输入 100 个数，每个数占一行，表示数组的所有元素的值。

每个数可能是整数也可能是浮点数。

输出格式
按顺序输出数组中的所有不大于 10 的元素，每个元素占一行。

输出格式为 A[i] = x，其中 i 为元素编号，x 为元素的值。

注意，所有的 x 均保留一位小数。

数据范围
−100≤A[i]≤100
输入样例：
0
-5
63
-8.5
…
输出样例：
A[0] = 0.0
A[1] = -5.0
A[3] = -8.5
…

#include

using namespace std;

const int N = 105;

double a[N];

int main()
{
    for(int i = 0; i < 100; i++)
    {
        scanf("%lf", &a[i]); //double 用 %d ，则a[i]不会读入数据 
        if(a[i] <= 10.0)
            printf("A[%d] = %.1lf\n", i, a[i]);
    }
    return 0;
}

740. 数组变换

输入一个长度为 20 的整数数组 N，将整个数组翻转，使得第一个元素成为倒数第一个元素，第二个元素成为倒数第二个元素，…，倒数第二个元素成为第二个元素，倒数第一个元素成为第一个元素。

输出翻转后的数组。

输入格式
输入包含 20 个整数，每个数占一行。

输出格式
输出新数组中的所有元素，每个元素占一行。

输出格式为 N[i] = x，其中 i 为元素编号（从 0 开始），x 为元素的值。

数据范围
−100≤N[i]≤100
输入样例：
0
-5
…
63
23
输出样例：
N[0] = 23
N[1] = 63
…
N[18] = -5
N[19] = 0

#include 
#include
using namespace std;

const int N = 20;

int a[N];

int main()
{
  for(int i = 0; i < 20; i++) scanf("%d", &a[i]);
  //for(int i = 0; i < 20; i++) printf("N[%d] = %d\n", i, a[20 - i - 1]); 下标逆序计算
  reverse(a, a + 20); //函数法
  for(int i = 0; i < 20; i++) printf("N[%d] = %d\n", i, a[i]);

  return 0;
}

old_code

#include 
using namespace std;
int a[20];
int main()
{
  for(int i=0; i < 20; i++)
  {
    cin>>a[i];
  }
  for(int i = 19; i >=0 ; i--)
  {
    printf("N[%d] = %d\n",abs(i - 19), a[i]);
  }
  return 0;
}

741. 斐波那契数列

输入整数 N，求出斐波那契数列中的第 N 项是多少。

斐波那契数列的第 0 项是 0，第 1 项是 1，从第 2 项开始的每一项都等于前两项之和。

输入格式
第一行包含整数 T，表示共有 T 个测试数据。

接下来 T 行，每行包含一个整数 N。

输出格式
每个测试数据输出一个结果，每个结果占一行，

结果格式为 Fib(N) = x，其中 N 为项数，x 为第 N 项的值。

数据范围
0≤N≤60
输入样例：
3
0
4
2
输出样例：
Fib(0) = 0
Fib(4) = 3
Fib(2) = 1

#include

using namespace std;

typedef long long LL; 

const int N = 65;

LL fib[N] = {0,1}; 

int main()
{
    fib[0] = 0, fib[1] = 1;
    for(int i = 2 ; i<= 60 ; i++) fib[i] = fib[i - 1] + fib[i - 2]; 
    int T;
    scanf("%d", &T);
    while(T--)
    {
        int n;
        scanf("%d", &n);
        printf("Fib(%lld) = %lld\n", n, fib[n]);  // LL ~~~~  scanf("%lld", )
        //cout<<"Fib(" << n << ") = "<< fib[n] << endl;
    }
    return 0;
}

递推

#include 

using namespace std;

typedef long long LL;

int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        int n;
        scanf("%d", &n);
        LL a = 0, b = 1, c;
        for(int i = 0; i <= n; i++) //递推没有存下来时间复杂度高
        {
          if (i == n) printf("Fib(%d) = %lld\n", n, a); //a从第0项开始,不断往后移动, i从0开始 ：a每轮为第i项
          c = a + b;
          a = b;
          b = c;
        }
    }
      return 0;
}

742. 最小数和它的位置

输入一个整数 N 和一个长度为 N 的整数数组 X。

请你找到数组中最小的元素，并输出它的值和下标。

注意，如果有多个最小值，则返回下标最小的那个。

输入格式
第一行包含整数 N。

第二行包含 N 个用空格隔开的整数 X[i]。

输出格式
第一行输出 Minimum value: x，其中 x 为数组元素最小值。

第二行输出 Position: y，其中 y 为最小值元素的下标（下标从 0 开始计数）。

数据范围
1 −1000≤X[i]≤1000
输入样例：
10
1 2 3 4 -5 6 7 8 9 10
输出样例：
Minimum value: -5
Position: 4

简版

#include

using namespace std;

const int N = 1010;

int n;
int q[N];

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i++)  scanf("%d", &q[i]);
    
    int minv = 1e4, min_idx;  
    for(int i = 0; i < n; i++)
        if(minv > q[i]) 
        {
            minv = q[i];
            min_idx = i;
        }
    
    printf("Minimum value: %d\nPosition: %d", minv, min_idx);
    
    return 0;
}

容器版

#include
#include

using namespace std;

int n;
vector<int> q;

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i++)
    {
        int x;
        scanf("%d", &x);
        q.push_back(x); 
    }
    
    int minv = 1e4, min_idx;  
    //for(vector::iterator it = q.begin() ; it != q.end() ; it++)   //不好表示下标：需多一个变量
    int len = q.size();
    for(int i = 0; i < q.size(); i++)
        if(minv > q[i]) 
        {
            minv = q[i];
            min_idx = i;
        }
    
    printf("Minimum value: %d\nPosition: %d", minv, min_idx);
    
    return 0;
}

743. 数组中的行

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组中某一列的元素的平均值或元素的和。

输入格式
第一行输入整数 C，表示所求的具体列数（列数从 0 开始计数）。

第二行包含一个大写字母，若为 S，则表示需要求出第 C 列的元素的和，若为 M，则表示需要求出第 C 列的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或元素的和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
1
S
-9.0 -2.4 -3.3 2.4 -9.7 -5.7 -5.3 6.5 -7.3 4.8 -4.1 3.9
1.6 -0.9 9.2 -7.5 1.0 -8.0 -4.1 -4.0 -0.1 -9.0 8.4 4.9
-8.2 -0.3 -5.1 -5.6 6.6 0.9 -1.0 -5.4 -2.1 -4.5 -8.7 -1.1
-4.2 6.5 -8.2 3.6 -4.6 -9.2 -1.7 6.9 -9.0 -9.8 7.7 -3.4
-8.0 5.7 4.8 0.3 -1.4 2.8 -6.3 9.3 0.3 6.3 1.5 -1.7
1.7 -0.0 9.7 -6.6 1.3 -2.0 -6.1 2.0 -7.8 -4.7 -9.1 6.0
-8.2 -1.7 9.4 -1.2 -1.0 -9.0 -7.0 -6.9 -1.6 -6.8 -6.7 1.8
4.8 1.3 -6.1 -0.6 0.5 -2.9 -6.8 1.5 5.8 3.2 0.0 7.7
6.3 1.1 4.7 7.3 7.6 5.6 0.9 9.2 1.3 -4.9 7.8 -4.9
0.5 3.5 -5.0 9.0 8.8 8.7 7.5 7.5 -9.6 -6.9 -1.6 6.9
7.8 5.6 -6.4 3.6 2.3 0.5 4.1 6.1 8.6 -9.3 2.2 -0.4
9.9 0.9 6.4 -2.8 -4.2 -7.6 0.6 9.6 3.0 0.9 5.1 4.5
输出样例：
19.3

#include
#include

using namespace std;

const int N = 13;

double q[N][N];  //用到精度 ： scanf的易错点就来了！！！ double ---> %lf ,  LL ---> %lld
double sum[N]; 

int main()
{
    int row; 
    char op;
    //cin >> row >> op; //scanf易错 %d %c
    scanf("%d %c", &row, &op);
    for(int i = 0; i < 12; i++)
        for(int j = 0; j < 12; j++)
        {
            scanf("%lf", &q[i][j]);
            sum[i] += q[i][j]; 
        }
            
    if(op == 'S') printf("%.1lf", sum[row]); //格式输出 printf方便
    else printf("%.1lf", sum[row] / 12);    //压缩代码printf("%.1lf",op=='S' ? sum[row] : sum[row] / 12);
        
    return 0;
}

y总

#include 
#include 

using namespace std;

int main()
{
    int n;
    char op;

    double matrix[12][12];

    cin >> n >> op;
    for (int i = 0; i < 12; i ++ )
        for (int j = 0; j < 12; j ++ )
            cin >> matrix[i][j];

    double s = 0;
    for (int i = 0; i < 12; i ++ ) s += matrix[n][i];

    if (op == 'M') s /= 12;//先求和, 如果求平均就 / 12.0

    printf("%.1lf\n", s);

    return 0;
}



/*简洁版
#include 

using namespace std;

int main()
{
    int l;
    char op;
    cin >> l >> op;
    double s=0;
    for(int i=0;i<12;i++)
    {
        for(int j=0;j<12;j++)
        {
            double a;
            cin >> a;
            if(i==l) s+=a;
        }
    }

    printf("%.1lf",op=='S' ? s : s/12);
}

*/

744. 数组中的列

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组中某一列的元素的平均值或元素的和。

输入格式
第一行输入整数 C，表示所求的具体列数（列数从 0 开始计数）。

第二行包含一个大写字母，若为 S，则表示需要求出第 C 列的元素的和，若为 M，则表示需要求出第 C 列的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或元素的和的值，保留一位小数。

浮点数读入

#include

using namespace std;

const int N = 13;

double sum; //浮点数 - 警觉
double q[N][N];

int main()
{
    int n;
    char op;
    scanf("%d %c", &n, &op);
     
    for(int i = 0; i < 12; i++)
        for(int j = 0; j < 12; j++)
        {
            scanf("%lf", &q[i][j]); //浮点数 - 警觉
            if(j == n) sum += q[i][j]; //第n列的和(下标从0开始)
        }
        
    if(op == 'S') printf("%.1lf", sum);
    else printf("%.1lf", sum / 12);
    
    return 0;
}

c++版


#include
using namespace std;

int main()
{
    int n,i,j;
    char ch;
    double s,t;
    cin>>n>>ch;
    for(i=0;i<=11;i++)
        for(j=0;j<=11;j++){
            cin>>t;
            if(j==n)s=s+t; //只要j等于n，就累加
        }
    cout<<fixed<<setprecision(1);    
    if(ch=='S') cout<<s;
   	else cout<<s/12;
    //printf("%.1lf", ch == 'S' ? c : c / 12);
	return 0;
}

此类题目写出对角线，就是简单的数学空间区域交集划分

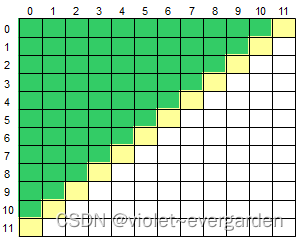
745. 数组的右上半部分

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的右上半部分元素的平均值或元素的和。

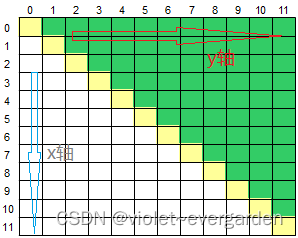
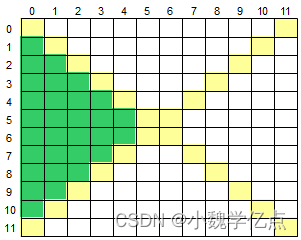
右上半部分是指主对角线上方的部分，如下图所示，黄色部分为对角线，绿色部分为右上半部分：

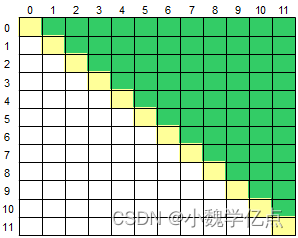
输入格式
第一行输入一个大写字母，若为 S，则表示需要求出右上半部分的元素的和，若为 M，则表示需要求出右上半部分的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或元素的和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
M
-6.5 8.2 0.7 9.0 0.8 -4.3 0.9 -0.0 -7.9 7.1 -1.6 4.6
-9.4 -9.0 1.5 -9.0 -5.1 -0.5 -2.8 -9.1 8.0 -6.9 -5.5 -6.6
-6.8 0.3 3.8 6.1 -9.9 -9.3 8.5 8.6 5.0 6.9 -3.6 -3.0
-0.8 -1.6 -7.3 -6.7 4.4 -9.1 -9.0 1.6 0.3 -6.0 6.0 -0.8
-0.8 -6.0 -4.9 -3.9 6.4 6.2 -4.2 -0.9 7.9 1.6 -8.2 -9.2
7.8 -5.8 -5.8 -5.8 7.2 0.5 -7.9 1.2 -6.8 -9.1 0.3 -1.4
4.3 -7.2 3.5 -6.4 -9.1 -6.0 3.5 -5.1 -5.6 -6.9 -9.1 -2.1
-7.6 -7.1 0.7 -1.7 5.0 -9.0 1.4 -6.2 7.6 4.8 -7.5 4.0
-0.2 0.3 -4.2 8.4 0.7 -6.4 -2.7 3.5 -0.9 3.7 0.9 -2.7
7.1 0.1 8.4 -5.1 -7.9 -0.5 -5.3 -5.7 -4.6 9.6 -8.3 7.0
9.6 -9.8 3.3 -9.9 -6.8 6.7 3.1 1.2 -9.5 -4.3 -1.7 -9.7
1.8 5.0 8.3 -0.7 -0.9 3.2 2.5 0.5 7.3 8.3 0.3 0.9
输出样例：
-1.2

注意看图【判断与数组下标关系】

图中绿色求和部分：y > x ----> j > i

绿色部分：【下标】：倒头看：数组下标对应： y = x分界线（副对角线）， y = -x (正对角线)

#include

using namespace std;

const int N = 13;
double q[N][N], sum;

int main()
{
    char op;
    scanf("%c\n", &op);
    
    for(int i = 0; i < 12; i++) //一个看图误区：需翻转90度看, 对角线应该为:y = x ---> 右上半部分 ： y > x
        for(int j = 0; j < 12; j++)
        {
            scanf("%lf", &q[i][j]);
            if(j > i)  //【下标】：倒头看：数组下标对应： y = x分界线（副对角线）  ， y = -x (正对角线)
                sum += q[i][j];
        }
            
    if(op == 'S') printf("%.1lf", sum);
    else printf("%.1lf", sum / 66.0);  //个数  11 * (11 + 1) / 2  
    
       
    return 0;
}

746. 数组的左下半部分

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的左下半部分元素的平均值或元素的和。

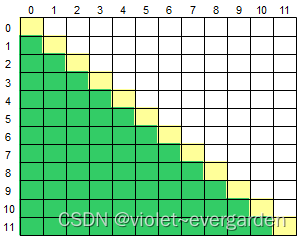
左下半部分是指主对角线下方的部分，如下图所示，黄色部分为对角线，绿色部分为左下半部分：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出左下半部分的元素的和，若为 M，则表示需要求出左下半部分的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
S
8.7 5.6 -2.0 -2.1 -7.9 -9.0 -6.4 1.7 2.9 -2.3 8.4 4.0
-7.3 -2.1 0.6 -9.8 9.6 5.6 -1.3 -3.8 -9.3 -8.0 -2.0 2.9
-4.9 -0.5 -5.5 -0.2 -4.4 -6.1 7.6 6.9 -8.0 6.8 9.1 -8.5
-1.3 5.5 4.6 6.6 8.1 7.9 -9.3 9.6 4.6 0.9 -3.5 -4.3
-7.0 -1.2 7.0 7.1 -5.7 7.8 -2.3 4.3 0.2 -0.4 -6.6 7.6
-3.2 -5.4 -4.7 4.7 3.6 8.8 5.1 -3.1 -2.9 2.8 -4.3 -1.4
-1.8 -3.3 -5.6 1.8 8.3 -0.5 2.0 -3.9 -1.0 -8.6 8.0 -3.3
-2.5 -9.8 9.2 -0.8 -9.4 -0.5 1.6 1.5 3.4 -0.1 7.0 -6.2
-1.0 4.9 2.2 -8.7 -0.9 4.8 2.3 2.0 -3.2 -7.5 -4.0 9.9
-1.1 -2.9 8.7 3.6 7.4 7.8 10.0 -9.0 1.6 8.3 6.3 -5.8
-9.9 0.6 2.0 -3.8 -6.3 0.6 7.3 3.8 -7.1 9.5 2.2 1.3
-2.8 -9.1 7.1 -0.2 0.6 -6.5 1.1 -0.1 -3.6 4.0 -5.4 1.1
输出样例：
-2.8

取两个坐标计算直线【副对角线】: y = -x + 11

#include

using namespace std;

const int N = 13;
double q[N][N], sum;

int main()
{
    char op;
    scanf("%c\n", &op);

    for(int i = 0; i < 12; i++) //一个看图误区：需翻转90度看, 对角线应该为:y = x ---> 右上半部分 ： y > x
        for(int j = 0; j < 12; j++)
        {
            scanf("%lf", &q[i][j]);
            if(j < -i + 11)  //【下标】：倒头看：数组下标对应： y = x分界线（副对角线）  ， y = -x (正对角线)
                sum += q[i][j];
        }

    if(op == 'S') printf("%.1lf", sum);
    else printf("%.1lf", sum / 66.0);  //个数  11 * (11 + 1) / 2  

    return 0;
}

747. 数组的左上半部分

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的左上半部分元素的平均值或元素的和。

左上半部分是指次对角线上方的部分，如下图所示，黄色部分为对角线，绿色部分为左上半部分：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出左上半部分的元素的和，若为 M，则表示需要求出左上半部分的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
M
-0.4 -7.7 8.8 1.9 -9.1 -8.8 4.4 -8.8 0.5 -5.8 1.3 -8.0
-1.7 -4.6 -7.0 4.7 9.6 2.0 8.2 -6.4 2.2 2.3 7.3 -0.4
-8.1 4.0 -6.9 8.1 6.2 2.5 -0.2 -6.2 -1.5 9.4 -9.8 -3.5
-2.3 8.4 1.3 1.4 -7.7 1.3 -2.3 -0.1 -5.4 -7.6 2.5 -7.7
6.2 -1.5 -6.9 -3.9 -7.9 5.1 -8.8 9.0 -7.4 -3.9 -2.7 0.9
-6.8 0.8 -9.9 9.1 -3.7 -8.4 4.4 9.8 -6.3 -6.4 -3.7 2.8
-3.8 5.0 -4.6 2.0 4.0 9.2 -8.9 0.5 -3.9 6.5 -4.3 -9.9
-7.2 6.2 -1.2 4.1 -7.4 -4.6 4.7 -0.4 -2.2 -9.1 0.4 -5.8
9.1 -6.4 9.2 0.7 10.0 -5.7 -9.7 -4.4 4.7 4.7 4.9 2.1
-1.2 -6.2 -8.2 7.0 -5.3 4.9 5.5 7.2 3.4 3.2 -0.2 9.9
-6.9 -6.2 5.1 8.5 7.1 -0.8 -0.7 2.7 -6.0 4.2 -8.2 -9.8
-3.5 7.7 5.4 2.8 1.6 -1.0 6.1 7.7 -6.5 -8.3 -8.5 9.4
输出样例：
-0.8

取两个坐标计算直线【副对角线】: y = -x + 11

#include

using namespace std;

const int N = 13;
double q[N][N], sum;

int main()
{
    char op;
    scanf("%c\n", &op);

    for(int i = 0; i < 12; i++) //一个看图误区：需翻转90度看, 对角线应该为:y = x ---> 右上半部分 ： y > x
        for(int j = 0; j < 12; j++)
        {
            scanf("%lf", &q[i][j]);
            if(j < -i + 11)  //【下标】：倒头看：数组下标对应： y = x分界线（副对角线）  ， y = -x (正对角线)
                sum += q[i][j];
        }

    if(op == 'S') printf("%.1lf", sum);
    else printf("%.1lf", sum / 66.0);  //个数  11 * (11 + 1) / 2  

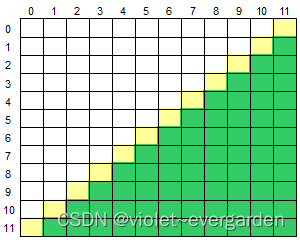
    return 0;
}

748. 数组的右下半部分

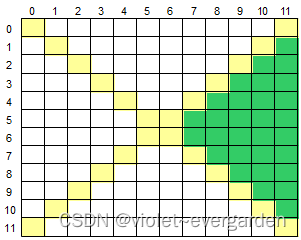
输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的右下半部分元素的平均值或元素的和。

右下半部分是指次对角线下方的部分，如下图所示，黄色部分为对角线，绿色部分为右下半部分：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出右下半部分的元素的和，若为 M，则表示需要求出右下半部分的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
S
9.7 -4.9 6.1 -6.1 -9.6 1.0 -3.2 0.6 3.2 -9.8 4.9 1.2
-2.8 -5.3 2.8 -1.9 -5.4 7.5 -2.0 5.7 2.3 5.3 -7.5 8.9
6.0 4.3 3.8 -6.7 8.1 -0.5 7.8 -2.2 -1.0 4.0 -4.9 -9.4
5.4 3.7 -6.5 -3.9 -3.3 4.1 -2.5 -4.7 8.2 1.4 1.8 4.7
2.4 9.0 -4.3 9.6 8.6 -6.1 -7.4 8.6 5.6 0.5 -0.4 5.2
-5.2 2.9 -5.6 4.0 -0.2 3.8 -4.1 -1.6 -3.8 -3.1 -1.1 3.3
-9.4 -1.4 0.6 6.5 -4.3 -8.3 6.1 2.9 -5.2 2.5 9.8 -7.7
-2.9 -3.6 7.9 -5.8 -4.7 8.2 -6.2 1.0 7.4 -1.0 -4.4 -4.5
0.1 9.5 4.9 1.5 0.8 -8.2 0.4 9.5 -0.8 -0.9 9.7 -2.1
0.1 -7.6 7.8 -6.9 5.5 1.4 4.0 7.8 1.0 -1.2 9.7 -1.9
-4.6 2.3 -5.5 8.2 -4.8 -3.7 5.4 0.2 -2.4 -0.8 7.4 0.0
-0.1 8.2 0.8 -3.5 -7.6 -0.5 5.6 8.4 -8.6 0.9 9.0 -7.5
输出样例：
53.0

#include

using namespace std;

const int N = 13;
double q[N][N], sum;

int main()
{
    char op;
    scanf("%c\n", &op);

    for(int i = 0; i < 12; i++) //一个看图误区：需翻转90度看, 对角线应该为:y = x ---> 右上半部分 ： y > x
        for(int j = 0; j < 12; j++)
        {
            scanf("%lf", &q[i][j]);
            if(j > -i + 11)  //【下标】：倒头看：数组下标对应： y = x分界线（副对角线）  ， y = -x (正对角线)
                sum += q[i][j];
        }

    if(op == 'S') printf("%.1lf", sum);
    else printf("%.1lf", sum / 66.0);  //个数  11 * (11 + 1) / 2  


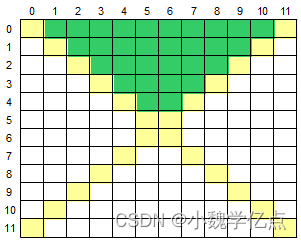
    return 0;
}

749. 数组的上方区域

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的上方区域元素的平均值或元素的和。

数组的两条对角线将数组分为了上下左右四个部分，如下图所示，黄色部分为对角线，绿色部分为上方区域：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出上方区域的元素的和，若为 M，则表示需要求出上方区域的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

输出结果与标准答案据对误差不超过 0.1 即视为正确。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
S
-4.8 -8.0 -2.9 6.7 -7.0 2.6 6.5 1.7 1.9 5.6 -1.6 -6.3
-4.3 1.5 8.7 -0.3 5.4 -9.3 4.8 7.0 3.6 -8.3 -1.0 1.3
-9.9 9.7 -6.3 5.8 2.9 2.9 -7.7 4.9 -0.6 7.2 6.4 7.7
2.8 -5.8 -0.0 2.2 4.0 7.7 -3.0 -7.5 -3.5 9.7 -4.3 -8.6
-1.8 -0.1 5.4 0.6 9.9 -3.7 -1.1 0.8 -0.2 -0.0 9.9 4.5
3.0 -3.9 2.1 -9.7 5.5 9.4 -4.6 3.3 -9.6 5.1 -4.5 1.5
4.3 -5.4 -7.9 9.2 -7.7 -9.6 -1.5 -1.6 -7.2 2.0 -3.7 -0.7
8.0 2.8 -4.1 7.1 8.4 -5.6 3.9 -9.7 -1.1 3.0 -8.5 -3.3
1.7 5.1 0.1 9.2 4.5 9.7 7.2 8.6 8.7 1.1 6.7 0.3
-3.6 -7.1 -8.9 7.1 -5.9 1.6 -7.4 6.7 3.9 4.3 -2.4 -3.7
8.9 -6.2 5.0 -8.6 -1.3 -8.8 2.6 8.9 5.5 9.0 -2.2 -4.4
5.7 3.7 1.8 -2.1 -7.3 -7.9 4.7 6.0 3.3 -2.8 1.4 -6.9
输出样例：
21.7

上半部 = [右上部&&左上部] ：公共部分 j > i&& j + i < 11
两条对角线 y = x 与 y = -x + 11

#include

using namespace std;

const int N = 13;
double q[N][N], sum;

int main()
{
    char op;
    scanf("%c", &op);
        
    for(int i= 0; i < 12 ; i++)
        for(int j = 0 ;j < 12; j++)
        {
            scanf("%lf", &q[i][j]);
            if(j > i && j < -i + 11) sum += q[i][j]; 
        }
               
    if(op == 'S') printf("%.1lf", sum);           
    else printf("%.1lf", sum / 30); // (10 + 2) * 5 / 2 == 30
               
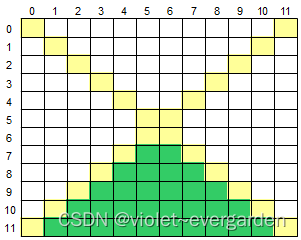
    return 0;
}

750. 数组的下方区域

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的下方区域元素的平均值或元素的和。

数组的两条对角线将数组分为了上下左右四个部分，如下图所示，黄色部分为对角线，绿色部分为下方区域：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出下方区域的元素的和，若为 M，则表示需要求出下方区域的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
S
-6.0 0.7 -8.4 -5.7 -4.1 7.6 9.5 -9.7 4.1 0.6 -6.5 -4.9
6.6 4.9 -3.1 5.3 0.3 -4.5 3.9 -1.5 6.6 7.0 5.1 2.5
-8.5 1.8 -2.7 0.1 -4.9 -7.2 4.3 6.0 -1.4 2.7 -3.0 2.0
4.8 -7.0 -1.3 0.8 1.0 4.5 -1.1 -2.9 -3.9 -3.9 -8.9 5.8
-2.1 -9.6 5.1 0.2 1.0 -1.7 6.4 4.1 2.8 -6.9 2.4 9.3
-6.0 -9.1 -7.0 -7.0 7.8 5.1 6.9 -7.6 0.4 -7.2 5.5 6.0
-1.9 5.5 1.9 -8.5 -5.3 2.3 -9.3 2.0 -0.2 1.2 5.6 -1.8
8.2 2.3 3.5 1.4 4.0 -5.1 -6.9 -2.8 1.7 -7.0 7.8 1.8
-6.0 -4.1 -4.6 -9.4 -4.9 -4.1 4.2 6.3 -2.8 8.7 8.1 -0.9
8.8 -6.5 -4.3 6.1 -6.2 -3.9 -7.0 7.3 5.0 -0.9 -0.0 5.6
-2.4 1.4 8.5 -2.2 0.9 5.3 3.6 8.8 -8.1 3.0 -3.1 6.5
-3.8 -6.4 2.3 4.2 -9.8 -0.3 -9.9 -7.4 3.5 1.5 -0.2 7.0
输出样例：
-11.9

#include

using namespace std;

const int N = 13;
double q[N][N], sum;

int main()
{
    char op;
    scanf("%c", &op);
        
    for(int i= 0; i < 12 ; i++)
        for(int j = 0 ;j < 12; j++)
        {
            scanf("%lf", &q[i][j]);
            if(j < i && j > -i + 11) sum += q[i][j]; 
        }
               
    if(op == 'S') printf("%.1lf", sum);           
    else printf("%.1lf", sum / 30); 
               
    return 0;
}

751. 数组的左方区域

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的左方区域元素的平均值或元素的和。

数组的两条对角线将数组分为了上下左右四个部分，如下图所示，黄色部分为对角线，绿色部分为左方区域：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出左方区域的元素的和，若为 M，则表示需要求出左方区域的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0

mycode2022

#include

using namespace std;

const int N = 13;
double q[N][N], sum;

int main()
{
    char op;
    scanf("%c", &op);
        
    for(int i= 0; i < 12 ; i++)
        for(int j = 0 ;j < 12; j++)
        {
            scanf("%lf", &q[i][j]);
            if(j < i && j < -i + 11) sum += q[i][j]; 
        }
               
    if(op == 'S') printf("%.1lf", sum);           
    else printf("%.1lf", sum / 30); 
               
    return 0;
}

哈夫曼距离


#include
#include
int main(){
    char a;
    scanf("%c", &a);
    double n[15][15];
    for(int i = 0; i <12 ;i++){
        for(int j = 0; j < 12; j++){
            scanf("%lf", &n[i][j]);
        }
    }
    double sum = 0;
    int c = 0;  //加计数器，不用自己算平均数分母
    for(int i = 0; i < 12; i++){
        for(int j = 0; j < 12; j++){
            if((abs(5.5-i)+j) <= 4.5){   //麦哈顿距离  （比较不好想）
                sum += n[i][j];
                c++;  
            }

        }
    }
    if(a == 'S') printf("%.1lf", sum);
    else printf("%.1lf", sum / c);
    return 0;
}

法二：等效上半部矩阵转置【i,j互换位置】


#include
using namespace std;

char c;
double a[13][13],sum;
int main()
{
    scanf("%c\n",&c);

    for(int i = 0;i < 12;i++)
        for(int j = 0;j < 12;j++)
        {
            scanf("%lf",&a[i][j]);   //数组的左方区域:(i+j)<11 && i>j                             【左上 - 上半 - 交集中的对角线】
            if( i + j < 11 && i > j  )                                                           //不正确.. i < 11 && (j > i && j + i < 11) && j != i + 11
                sum += a[i][j];
        }

    if(c == 'S') printf("%.1lf",sum);
    else printf("%.1lf",sum/30);  // 与上半部分相同个数

    return 0;
}

曼尔顿距离用法【斜线适用 y = x或 -x + b】
①(边界斜线或对角线交点):起点坐标(x1,y1) 与(i,j)
② |x1-x2| + |y1-y2| <= distance (等于看边界是否可取)

752. 数组的右方区域

输入一个二维数组 M[12][12]，根据输入的要求，求出二维数组的右方区域元素的平均值或元素的和。

数组的两条对角线将数组分为了上下左右四个部分，如下图所示，黄色部分为对角线，绿色部分为右方区域：

输入格式
第一行输入一个大写字母，若为 S，则表示需要求出右方区域的元素的和，若为 M，则表示需要求出右方区域的元素的平均值。

接下来 12 行，每行包含 12 个用空格隔开的浮点数，表示这个二维数组，其中第 i+1 行的第 j+1 个数表示数组元素 M[i][j]。

输出格式
输出一个数，表示所求的平均数或和的值，保留一位小数。

数据范围
−100.0≤M[i][j]≤100.0
输入样例：
S
2.4 7.8 9.4 -5.6 6.9 -4.9 4.8 0.8 3.6 1.7 -1.4 9.7
-6.8 -3.7 -2.0 -4.9 -4.5 -5.3 6.1 7.5 -4.3 5.9 -9.5 9.7
-6.5 -0.4 1.6 3.7 -4.4 -3.3 1.9 7.7 -1.4 4.5 7.4 -3.0
-1.2 0.4 9.8 9.8 -4.3 -1.3 -1.6 0.5 2.8 -4.0 8.5 3.9
0.2 -2.0 -6.4 -9.8 3.7 -2.0 1.7 -3.6 -3.4 2.4 -1.2 -3.9
-8.3 5.8 -1.0 -4.4 1.0 -2.4 2.8 -4.6 2.1 8.7 -6.8 -8.3
6.3 -6.8 -7.0 9.3 -7.7 -1.7 8.2 -6.5 -1.8 6.7 8.2 4.4
0.4 8.6 -1.2 8.6 -4.6 1.8 9.6 1.6 2.0 -1.0 3.9 -9.2
7.5 -3.1 6.2 -4.5 -3.0 2.5 -7.7 2.9 0.3 3.3 -2.7 3.4
-5.0 3.0 -0.0 4.3 9.5 -0.0 -9.9 -8.6 -0.9 -5.5 7.7 6.5
4.9 -9.6 -2.9 8.5 2.0 -9.9 -4.9 -1.5 -2.4 -7.6 1.7 8.5
-6.4 6.8 -3.7 -4.7 0.2 5.8 -5.4 0.6 7.0 -4.2 -7.5 -2.4
输出样例：
40.9

753. 平方矩阵 I

输入整数 N，输出一个 N 阶的回字形二维数组。

数组的最外层为 1，次外层为 2，以此类推。

输入格式
输入包含多行，每行包含一个整数 N。

当输入行为 N=0 时，表示输入结束，且该行无需作任何处理。

输出格式
对于每个输入整数 N，输出一个满足要求的 N 阶二维数组。

每个数组占 N 行，每行包含 N 个用空格隔开的整数。

每个数组输出完毕后，输出一个空行。

数据范围
0≤N≤100
输入样例：
1
2
3
4
5
0
输出样例：
1

1 1
1 1

1 1 1
1 2 1
1 1 1

1 1 1 1
1 2 2 1
1 2 2 1
1 1 1 1

1 1 1 1 1
1 2 2 2 1
1 2 3 2 1
1 2 2 2 1
1 1 1 1 1

写的不错

规律：四个方向到自身的最短距离

#include

using namespace std;

int main()
{
    int n;
    while(scanf("%d", &n) && n)
    {
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < n; j++) //复合简写：min(min(i + 1, j + 1), min(n - i, n - j)) 
            {
                int x = min(i + 1, n - i); //选取x
                int y = min(j + 1, n - j); // 选取y
                int z = min(x, y); //选取最短
                printf("%d ", z);
            }
            puts("");
        }
        puts("");
    }
    return 0;
}

Chuckie写的很棒
曼哈顿距离法

①当n为奇数时, 找取中间点n / 2分别于行i列j的距离的最大值(max(abs(n / 2 - i), abs(n / 2 - j))),可以的如下图形(例如n == 5):
2 2 2 2 2
2 1 1 1 2
2 1 0 1 2
2 1 1 1 2
2 2 2 2 2
②观察结果, 随着回形越深入,内外围回形相差为1, 因此想到 (n + 1) / 2
③当n为偶数时，采用同样的方法, 这里我们就让中心点在图形的中间位置 (n - 1) / 2.0, 再求解其分别于行i列j的距离的最大值(max(abs((n - 1) / 2.0 - i), abs((n - 1) / 2.0 - j)))
④再考虑所得图形与实际结果相差值,这里我们依然设置(n + 1) / 2

#include 
#include 
#include 

using namespace std;

int main()
{
    int n;
    int a[100][100];

    while (cin >> n, n)   
    {
        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < n; j ++ )
            {
                if (n % 2) //n为奇数 
                {
                    a[i][j] = (n + 1) / 2 - max(abs(i - n / 2), abs(j - n / 2));     //中心点 (n / 2, n / 2 )
                }
                else //n为偶数 
                {
                    a[i][j] = n / 2 - max(min(abs(i - n / 2), abs(i - (n - 1) / 2)), min(abs(j - n / 2), abs(j - (n - 1) / 2)));
                }
            }

        for (int i = 0; i < n; i ++ )
        {
            for (int j = 0; j < n; j ++ ) printf("%d ", a[i][j]);
            puts("");
        }
        puts("");
    }
    return 0;
}

利用蛇形矩阵求解

①设置一个计数器统计方向改变次数
②设置变量res表示回形当前圈数
③其他部分与蛇形矩阵相同


#include 
#include 
#include 

using namespace std;

const int N = 100 + 10;
int m[N][N];

int main(){
    int n;
    int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};

    while(cin >> n, n ){
        memset(m, 0, sizeof m);
        int d = 1, x = 0, y = 0;
        int cnt = 0;  // 表示改变方向次数
        int res = 1;  // 回形当前圈数
        for (int i = 0; i < n * n; i ++){
            int a = x + dx[d], b = y + dy[d];
            m[x][y] = res;

            if (a < 0 || a >= n || b < 0 || b >= n || m[a][b]){
                d = (d + 1) % 4;
                a = x + dx[d], b = y + dy[d];
                cnt ++;
                if (!(cnt % 4)) res ++;
            }
            x = a, y = b;
        }

        for (int i = 0; i < n; i ++){
            for (int j = 0; j < n; j ++)
                cout << m[i][j] << ' ';
            cout << endl;
        }
        cout << endl;
    }

    return 0;
}

754. 平方矩阵 II

输入整数 N，输出一个 N 阶的二维数组。

数组的形式参照样例。

输入格式
输入包含多行，每行包含一个整数 N。

当输入行为 N=0 时，表示输入结束，且该行无需作任何处理。

输出格式
对于每个输入整数 N，输出一个满足要求的 N 阶二维数组。

每个数组占 N 行，每行包含 N 个用空格隔开的整数。

每个数组输出完毕后，输出一个空行。

数据范围
0≤N≤100
输入样例：
1
2
3
4
5
0
输出样例：
1

1 2
2 1

1 2 3
2 1 2
3 2 1

1 2 3 4
2 1 2 3
3 2 1 2
4 3 2 1

1 2 3 4 5
2 1 2 3 4
3 2 1 2 3
4 3 2 1 2
5 4 3 2 1

法一：每次向右延伸和向下延伸看

规律：每轮从(i, i)开始往右和往下单调递增填

#include

using namespace std;

const int N = 105;

int n;
int q[N][N];

int main()
{
    while(scanf("%d\n",&n), n)
    {
        for(int i = 0; i < n; i++)   
        {
            for(int j = i,k = 1; j <= n; j++, k++) //每轮都需从k = 1开始  , j = i 开始(不要覆盖之前填的)
            {
                q[i][j] = k; //向右延伸   
                q[j][i] = k; //向下延伸
            }
            
        }
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < n; j++)
            {
                printf("%d ",q[i][j]); 
            }
            puts("");
        }
        puts("");
    }
    
    return 0;
}

法二：正对角线(i, i)分界：左半向中间递增，右半递减填写每行
每行看：对角线前递增，对角线后递减 (不用数组，直接输出)

#include

using namespace std;

int n;

int main()
{
    while(scanf("%d\n",&n), n)
    {
        for(int i = 1;i <= n; i++)
        {
            for(int j = i; j >= 1; j--) printf("%d ",j);
            for(int j = i + 1; j <= n; j++) printf("%d ",j - i + 1);  //【从1开始时】
            puts("");
        }
        puts("");
    }
    
    return 0;
}

法三：下标与值规律

#include

using namespace std;

int n;

int main()
{
    while(scanf("%d\n",&n), n)
    {
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j < n; j++)
                printf("%d ", abs(j - i) + 1);  //【从1开始时，从0开始一样：|i-j|不变】
            puts("");
        }
         puts("");
    }
    
    return 0;
}

其他法：还可以当作对称矩阵解题：上三角 = 下三角对称值相等

755. 平方矩阵 III

输入整数 N，输出一个 N 阶的二维数组 M。

这个 N 阶二维数组满足 M[i][j]=2i+j。

具体形式可参考样例。

输入格式
输入包含多行，每行包含一个整数 N。

当输入行为 N=0 时，表示输入结束，且该行无需作任何处理。

输出格式
对于每个输入整数 N，输出一个满足要求的 N 阶二维数组。

每个数组占 N 行，每行包含 N 个用空格隔开的整数。

每个数组输出完毕后，输出一个空行。

数据范围
0≤N≤15
输入样例：
1
2
3
4
5
0
输出样例：
1

1 2
2 4

1 2 4
2 4 8
4 8 16

1 2 4 8
2 4 8 16
4 8 16 32
8 16 32 64

1 2 4 8 16
2 4 8 16 32
4 8 16 32 64
8 16 32 64 128
16 32 64 128 256

位运算：【 1 << (i + j)】

#include 

using namespace std;

int main()
{
    int n;

    while (scanf("%d", &n), n)
    {
        for (int i = 0; i < n; i ++ )
        {
            for (int j = 0; j < n; j ++ )
            {
                printf("%d ", 1 << (i + j));    //用位运算表示2的幂运算  【超快】
            }
            puts("");
        }
        puts("");
    }

    return 0;
}

改造平方矩阵Ⅱ

#include

using namespace std;

const int N = 105;

int n;
int q[N][N];

int main()
{
    while(scanf("%d\n",&n),n)
    {
        for(int i = 0;i < n;i++)   
        {
            for(int j = i,k = 1 << (i + j);j < n; j++ , k <<= 1) //i,j从0开始：每轮从k = 2^(i + j)开始 ; k *= 2
            {
                q[i][j] = k; //向右延伸   
                q[j][i] = k; //向下延伸
            }
            
        }
        for(int i = 0; i < n; i++)
        {
            for(int j = 0;j < n;j++)
            {
                printf("%d ",q[i][j]); 
            }
            puts("");
        }
        puts("");
    }
    
    return 0;
}

下标与值规律 (按i行从1开始)-----> $2 ^ i * 2 ^ j == 2 ^ {i + j}$


#include
using namespace std;

int n,t;
int main()
{
    while(scanf("%d\n",&n),n)
    {
        for(int i = 0;i < n;i++)
        {
            for(int j = 0;j < n;j++)
            {   
                t = 1;
                for(int k = 0;k < i + j ; k ++)
                {
                    t *= 2;
                }
                printf("%d ",t);  //  2^(i+j)     
            }
                
            printf("\n");
        }
        
         printf("\n");
    }
    
    return 0;
}

*756. 蛇形矩阵

输入两个整数 n 和 m，输出一个 n 行 m 列的矩阵，将数字 1 到 n×m 按照回字蛇形填充至矩阵中。

具体矩阵形式可参考样例。

输入格式
输入共一行，包含两个整数 n 和 m。

输出格式
输出满足要求的矩阵。

矩阵占 n 行，每行包含 m 个空格隔开的整数。

数据范围
1≤n,m≤100
输入样例：
3 3
输出样例：
1 2 3
8 9 4
7 6 5

向量枚举法

d与dx和dy初始值会影响输出结果！！！

#include

using namespace std;

const int N = 110;

int n,m;
int q[N][N];

int main()
{
    scanf("%d%d",&n,&m);
    int dx[] = {-1,0,1,0} , dy[] = {0,1,0,-1};//固定风格写：-1开始-1结束
    int x = 0,y = 0,d = 1;// d用于方向选择 1, 2, 3, 0 【上右下左】 d与dx和dy初始值会影响输出结果！！！
    //DFS搜索 【注意方向向量必须先判断右到不能走再往下走,再判断左, 再判断上(即此题固定右下左上)】
    for(int i = 1;i <= n * m;i++)   //【用i赋值且遍历n*m格 】
    {
        q[x][y] = i; //赋值：每轮填i
        int a = x + dx[d], b = y + dy[d];
        if(a < 0 ||a >= n || b < 0 || b >= m || q[a][b])  //【出界或(a,b)已填过不能走,判断下一个方向】 
        {
            d = (d+1) % 4;//判断下一个方向  【方向循环*妙*】
            a = x + dx[d], b = y + dy[d];
        }
        x = a ,y = b; // 新起点
    }
    
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j < m;j++)
        {
            printf("%d ",q[i][j]);            
        }
        puts("");
    }
    
    return 0;
}

/*

#include 
#include 
#include 

using namespace std;

const int N = 110;

int n, m;
int a[N][N];

void print2D(int x, int y, int val, int dir)
{
    if (val == n * m) return;
        
    switch(dir){
        case 0:
            while (a[x][y + 1] == 0)
                y ++, val ++, a[x][y] = val;
            print2D(x, y, val, 1);
            break;
        case 1:
            while (a[x + 1][y] == 0)
                x ++, val ++, a[x][y] = val;
            print2D(x, y, val, 2);
            break;
        case 2:
            while (a[x][y - 1] == 0)
                y --, val ++, a[x][y] = val;
            print2D(x, y, val, 3);
            break;
        case 3:
            while (a[x - 1][y] == 0)
                x --, val ++, a[x][y] = val;
            print2D(x, y, val, 0);
            break;
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i <= n + 1; i ++ )
        a[i][0] = a[i][m + 1] = -1;
    for (int j = 0; j <= m + 1; j ++ )
        a[0][j] = a[n + 1][j] = -1;
    print2D(1, 0, 0, 0);
    for (int i = 1; i <= n; i ++ ){
        for (int j = 1; j <= m; j ++ )
            cout << a[i][j] << ' ';
        cout << endl;
    }
    return 0;
}
*/


/*
#include 
#include 
#include 

using namespace std;

const int N = 110;

int n, m, a[N][N];

bool check(int x, int y){
    return x > 0 && x <= n && y > 0 && y <= m;
}

int main()
{
    cin >> n >> m;
    int x = 1, y = 0, val = 0;
    while (val != n * m)
    {
        while (check(x, y + 1) && a[x][y + 1] == 0)
            ++ y, ++ val, a[x][y] = val;
        while (check(x + 1, y) && a[x + 1][y] == 0)
            ++ x, ++ val, a[x][y] = val;
        while (check(x, y - 1) && a[x][y - 1] == 0)
            -- y, ++ val, a[x][y] = val;
        while (check(x - 1, y) && a[x - 1][y] == 0)
            -- x, ++ val, a[x][y] = val;
    }
    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ )
            cout << a[i][j] << ' ';
        cout << endl;
    }
    return 0;
}

*/