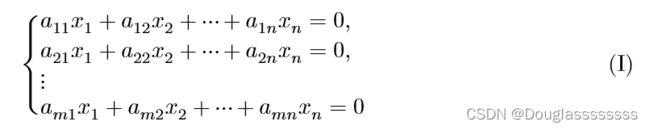【考研数学】线形代数第三章——向量 | 1）基本概念、向量组的相关性与线性表示

---

引言

向量是线性代数的重点和难点。向量是矩阵，同时矩阵又是由向量构成的，向量组与矩阵的关系非常紧密。

---

一、向量的概念与运算

1.1 基本概念

向量——既有大小（长度）又有方向的量称为向量，$(a_1,a_2,\dots ,a_n{)}^T,(a_1,a_2,\dots ,a_n)$ 分别称为 $n$ 维列向量和 $n$ 维行向量，其中 $a_i$ 称为向量的 $n$ 个分量，一般情况下我们所指的向量为列向量。

向量的模——设向量 $\alpha =(a_1,a_2,\dots ,a_n{)}^T$ ，称 $\sqrt{a_1^2+a_2^2+\cdots +a_n^2}$ 为向量 $\alpha$ 的模或长度，记为 $|\alpha |.$

向量的单位化——设向量 $\alpha =(a_1,a_2,\dots ,a_n{)}^T$ 为非零向量，与向量 $\alpha$ 方向相同且长度为 1 的向量称为 $\alpha$ 对应的单位向量，令 $${\alpha }^0=\frac{1}{|\alpha |}\alpha ,$$ 则称 ${\alpha }^0$ 为向量 $\alpha$ 的单位化向量。

向量的三则运算——加、减、与一个常数相乘。

向量的内积——设向量 $\alpha =(a_1,a_2,\dots ,a_n{)}^T$ ，设向量 $\beta =(b_1,b_2,\dots ,b_n{)}^T$ ，称 $a_1{b}_1+a_2{b}_2+\cdots +a_n{b}_n$ 为向量 $\alpha ,\beta$ 的内积，记为 $(\alpha ,\beta ).$

1.2 向量运算的性质

（一）三则运算的性质

（二）向量内积运算的性质

1. $(\alpha ,\beta )=(\beta ,\alpha )={\alpha }^T\beta ={\beta }^T\alpha .$
2. $(\alpha ,\alpha )={\alpha }^T\alpha =|\alpha {|}^2,$ 且 $(\alpha ,\alpha )=0$ 的充要条件为 $\alpha =0.$
3. $(a,k_1{\beta }_1+k_2{\beta }_2+\cdots +k_n{\beta }_n)=k_1(\alpha ,{\beta }_1)+k_2({\alpha }_2,{\beta }_2)+\cdots +k_n(\alpha ,{\beta }_n).$
4. 若 $(\alpha ,\beta )=0$ ，即 $a_1{b}_1+a_2{b}_2+\cdots +a_n{b}_n=0$ ，称 $\alpha ,\beta$ 正交，记为 $\alpha \perp \beta$ ，特别地，零向量与任何向量正交。

---

二、向量组的相关性与线性表示

2.1 理论背景

对于齐次线性方程组：

以及非齐次线性方程组：

令 ${\alpha }_1=(a_{11},a_{21},\dots ,a_{m1}{)}^T,{\alpha }_2=(a_{12},a_{22},\dots ,a_{m2}{)}^T,\dots ,{\alpha }_n=(a_{1n},a_{2n},\dots ,a_{mn}{)}^T,b=(b_1,b_2,\dots ,b_m{)}^T$ ，则方程组（I）（II）可表示为如下向量形式：$$x_1{\alpha }_1+x_2{\alpha }_2+\cdots +x_n{\alpha }_n=0（I）$$$$x_1{\alpha }_1+x_2{\alpha }_2+\cdots +x_n{\alpha }_n=b（II）$$

1，设 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ 为向量组，称 $k_1{\alpha }_1+k_2{\alpha }_2+\cdots +k_n{\alpha }_n$ 为向量组 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ 的线性组合。
2，设 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ 为向量组，$b$ 为一个向量，若存在一组数 $k_1,k_2,\dots ,k_n$ ，使得 $b=k_1{\alpha }_1+k_2{\alpha }_2+\cdots +k_n{\alpha }_n$ ，称向量 $b$ 可由向量组 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ 线性表示。

2.2 相关性与线性表示基本概念

（一）相关性

对齐次线性方程组 $$x_1{\alpha }_1+x_2{\alpha }_2+\cdots +x_n{\alpha }_n=0（\ast ）$$ （1）若方程组（*）只有零解，则向量组 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ 线性无关。

（2）若方程组（*）有非零解，即存在一组不全为零的数 $k_1,k_2,\dots ,k_n$ 使得 $$k_1{\alpha }_1+k_2{\alpha }_2+\cdots +k_n{\alpha }_n=0,$$ 称向量组 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ 线性相关。

（二）线性表示

对非齐次线性方程组 $$x_1{\alpha }_1+x_2{\alpha }_2+\cdots +x_n{\alpha }_n=b（\ast \ast ）$$ （1）若方程组（**）有解，即存在常数 $k_1,k_2,\dots ,k_n$ ，使得 $b=k_1{\alpha }_1+k_2{\alpha }_2+\cdots +k_n{\alpha }_n$ ，称向量 $b$ 可由向量组 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ 线性表示。

（2）若方程组（**）无解，称向量 $b$ 不可由向量组 ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ 线性表示。

2.3 向量组相关性与线性表示的性质

这一块内容多，放在下一篇文章。