Iterative Reconstruction Based on Latent Diffusion Model for Sparse Data Reconstruction

基于潜在扩散模型的稀疏数据迭代重建

论文地址： https://arxiv.org/abs/2307.12070

项目地址：code will be publicly available.

Abstract

从稀疏测量重建计算机断层扫描(CT)图像是一个众所周知的不适定反问题。迭代重构(IR)算法是求解逆问题的一种方法。然而，最近的IR方法需要成对数据和逆投影矩阵的近似。为了解决这些问题，我们提出了潜在扩散迭代重建(LDIR)，这是一种开创性的zero-shot方法，它通过预训练的潜在扩散模型(LDM)作为准确有效的数据先验来扩展IR。LDIR通过无条件潜扩散模型近似先验分布，是第一个以无监督方式成功地将迭代重建与LDM相结合的方法。LDIR使得高分辨率图像的重建更加高效。此外，LDIR利用数据保真度项的梯度来指导LDM的采样过程，因此，LDIR不需要对逆投影矩阵进行近似，可以用一个模型解决各种CT重建任务。此外，为了提高重建的样本一致性，我们引入了一种利用历史梯度信息来引导梯度的新方法。我们在极其稀疏的CT数据重建任务上的实验表明，LDIR优于其他最先进的无监督方法，甚至超过了有监督方法，在数量和质量方面都是领先的技术。此外，LDIR在自然图像任务上也取得了具有竞争力的性能。值得注意的是，与具有类似网络设置的方法相比，LDIR还显示出更快的执行时间和更低的内存消耗。

1 Introduction

计算机断层扫描(CT)是现代医学中一项重要的医学成像技术，可以帮助医生诊断相关疾病。CT 测量是通过从不同角度对物体进行 X 射线投影来获得的。然而，在CT中使用x射线使人体暴露于潜在有害剂量的辐射，引起公众对辐射诱发疾病的担忧。因此，减少暴露剂量，如稀疏视图和有限角度成像，同时保持成像质量，对公众健康和医学诊断都有有益的意义，特别是在术中CT。由于信息稀疏，CT重建过程是众所周知的不适定逆问题。在过去的十年中，大量的工作集中在迭代重建(IR)，这被认为是CT重建的解决方案 Donoho (2006);candires et al .(2006)。迭代重建的目的是从噪声测量$y=Ax+n$中恢复信号$x$，其中$n$表示测量过程中的噪声，$A$是线性投影矩阵，通常将$x$映射到较低的维度。因此，典型的IR过程可表述如下：
$$\hat{x}=\arg \underset{x}{\min }\Vert \mathbf{A}x-y{\Vert }_2^2+\lambda R\left(x\right),\text{\hspace{1em}(1)}$$
其中，$||Ax-y|{|}_2^2$是保证重建结果与测量结果一致的数据保真度项，而$\lambda R(x)$是保证重建结果真实并遵循地真图像分布$p(x)$的先验项。

IR的关键挑战是找到合适的数据先验或稀疏变换来生成先验项。Beck, Teboulle (2009);Kim et al (2016);Zhao等人(2000)利用总变分、非局部均值或小波，通过手工制作的先验和逆投影矩阵的近似获得重建结果。受深度学习和神经网络成功的启发，最近的数据驱动方法Bora等人(2017);Chen等人(2018)通过学习先验和数值保真项取得了令人印象深刻的性能。然而，这些方法大多需要大规模的配对数据来训练它们的网络。此外，它们直接将测量结果投影到结果中，并且当探测器的几何形状发生变化时，它们也需要重新训练。Song et al(2022)方法虽然通过引入基于分数的生成模型解决了上述问题，但仍然需要知道逆投影矩阵的近似，这在实际应用中很难得到。此外，这些方法使用直接投影来代替数据保真度项，这使得它们需要针对不同的探测器几何形状设计不同的采样程序。

在本文中，我们提出了一种新的用于稀疏CT数据zero-shot重建的潜在扩散迭代重建(LDIR)方法。LDIR是第一个通过纳入潜在扩散模型来扩展传统IR技术的方法。具体来说，我们训练了一个潜在的无条件扩散模型来学习数据的分布。在逆向过程中，利用训练好的扩散模型代替常规IR中的先验项。特别地，为了从无条件扩散模型中生成指定先验，应用数据保真度项的梯度来指导扩散模型的采样过程。因此，我们不需要任何成对数据或测量矩阵的逆来训练我们的网络。此外，LDIR可以用一个模型解决多种CT重建任务。此外，通过在潜在空间中引导反向扩散采样过程，我们的zero-shot方法可以生成高分辨率的图像，并且具有令人印象深刻的性能。由于LDIR没有对数据保真度项做任何假设，我们可以使用任何可微的测量函数来保持数据的一致性。进一步，我们提出了一种新的引导策略，通过融合历史梯度自适应调整样本水平梯度，从而提高了zero-shot扩散模型的性能。

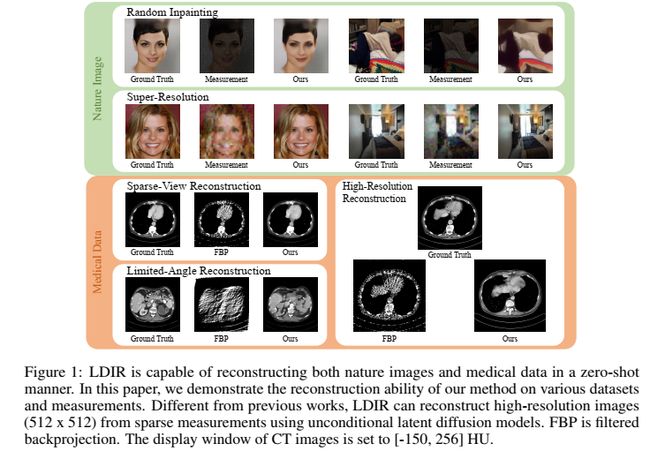
大量的实验表明，我们的方法优于最先进的监督和无监督方法，用于极其稀疏的CT数据重建。此外，由于CT图像和自然图像的迭代重建的共性，我们将LDIR扩展到自然图像恢复任务中，与其他最新的zero-shot方法相比，我们的方法取得了具有竞争力的性能。我们的方法为解决潜在扩散模型的逆问题提供了一个有价值的zero-shot工具，使我们能够利用大量可用的潜在扩散模型。图1显示了所提出方法的一些可视化结果。

2 Background

2.1 扩散模型

考虑一个$T$阶高斯扩散过程，其中$x_t\in {\mathbb{R}}^n,t\in [0，\dots ，T-1]$，初始$x_0$从原始数据分布$P_{data}$中采样。我们使用随机微分方程(SDE)来定义正向扩散过程Song et al (2021)：
$$dx=f\left(x,t\right)dt+g\left(t\right)dw,\text{\hspace{1em}(2)}$$
式中$f(\cdot ,t):{\mathbb{R}}^d\to {\mathcal{R}}^d$为漂移系数函数，$g(t)\in R$定义为扩散系数函数，$w\in {\mathbb{R}}^n$为标准n维布朗运动。因此，公式(2)的逆SDE也可以定义为：
$$dx=\left[f\left(x,t\right)-g{\left(t\right)}^2{\nabla }_x\log p_t\left(x\right)\right]dt+g\left(t\right)dw,\text{\hspace{1em}(3)}$$
$dt$是负的无穷小时间步长。反向SDE定义了一个生成过程，将标准高斯噪声转换为有意义的内容。为了完成这个转换，需要匹配分数函数${\nabla }_x\log p_t\left(x\right)$，在实践中通常用${\nabla }_x\log p_{0|t}\left(x_t|x_0\right)$代替。因此，我们可以训练一个分数模型$s_{\theta }\left(x,t\right)$，使$s_{\theta }\left(x,t\right)\approx {\nabla }_x\log p_t\left(x\right)\approx {\nabla }_x\log p_{0|t}\left(x_t|x_0\right)$，使用如下的分数匹配目标：
min ⁡ θ E t ∈ [ 0 , … , T − 1 ] , x 0 ∼ P d a t a , x t ∼ p 0 ∣ t ( x t ∣ x 0 ) [ ∣ ∣ s θ ( x , t ) − ∇ x log ⁡ p 0 ∣ t ( x t ∣ x 0 ) ∣ ∣ ∣ 2 2 ] . (4) \left.\min_{\theta}\mathbb{E}_{t\in[0,\ldots,T-1],x_{0}\sim P_{data},x_{t}\sim p_{0|t}(x_{t}|x_{0})}\left[\left|\left|s_{\theta}\left(x,t\right)-\nabla_{x}\log p_{0|t}\left(x_{t}|x_{0}\right)\right|\right|\right|_{2}^{2}\right]. \tag{4} θmin​Et∈[0,…,T−1],x0​∼Pdata​,xt​∼p0∣t​(xt​∣x0​)​[ ​ ​sθ​(x,t)−∇x​logp0∣t​(xt​∣x0​) ​ ​ ​22​].(4)
因此，通过迭代使用$s_{\theta }(x,t)$来估计分数${\nabla }_x\log p_t\left(x\right)$，反向SDE可以从随机噪声$x_{T-1}\sim \mathcal{N}(0,I)$中产生有意义的内容$x_0\sim P_{data}$。在我们的实验中，我们采用标准的去噪扩散概率模型(DDPM) Ho等(2020)，相当于上述方差保持SDE (VP-SDE Song等(2021))。

2.2 逆问题求解的扩散模型

为了使用扩散模型解决逆问题，提出了各种变通办法Rombach等人(2022);撒哈拉等人(2022年);Gao等(2023);Luo等人(2023)。这些方法利用条件扩散模型对高斯噪声进行迭代去噪，得到重构结果。然而，这些方法有局限性，因为它们依赖于需要成对数据进行训练的条件扩散模型，并且只能处理特定的任务而不需要再训练。为了解决这些问题，几个基于zero-shot扩散的逆求解器(Lugmayr等人(2022);Song et al . (2022);Kawar et al . (2022);Chung et al . (2022);Wang et al .(2023)已经提出。通常，假设$n\equiv 0$，对于每个去噪步骤，他们Lugmayr et al (2022);Song et al . (2022);Wang et al(2023)在前一步的基础上无条件估计新的去噪样本，然后使用测量值$A^{-1}y$替换去噪样本中的对应项，这也称为距离-零空间分解Wang et al(2023)。这种方法确保了数据的一致性，但在噪声测量的情况下失败，因为$A^{-1}y$不是去噪样本的正确对应项。为了解决这一限制，Chung等人(2023b,a)提出了替代方法来解决带噪声测量的逆问题。这些方法不是直接替换项目，而是使用梯度$||y-Ax|{|}_2^2$来有条件地指导生成过程。这些方法对噪声具有鲁棒性，并能处理非线性投影算子。然而，这些方法试图在像素空间上解决逆问题，并对数据保真度项做了很强的假设，这大大低估了现实世界问题的复杂性，无法重建高分辨率结果。

3 Method

3.1 扩散迭代重建

通常，可以将公式(1)中给出的IR方法转换为更通用的形式：
$$\begin{array}{rl}\hat{x}& =\arg \underset{x}{\min }E\left(x\right)\\ & =\arg \underset{x}{\min }\mathcal{U}\left(\mathbf{A}x,y\right)+\lambda R\left(x\right),\end{array}\text{\hspace{1em}(5)(6)}$$
其中$\mathcal{U}$是保证数据一致性的度量函数。假设测量函数和先验项都是可微的，可以对公式(6)应用梯度下降。这就产生了一个用于迭代重建的常微分方程(ODE)：
$$\begin{array}{rl}{x}_{t-1}& =x_t-\frac{\partial E\left(x\right)}{\partial x_t}\\ & =x_t-\left(ϵ{\nabla }_{x_t}\mathcal{U}\left(\mathbf{A}{x}_t,y\right)+{\lambda }_t{\nabla }_{x_t}R\left(x_t\right)\right),\end{array}\text{\hspace{1em}(7)(8)}$$
其中引导率$ϵ$和${\lambda }_t$用来平衡一致性和真实性。在实践中，我们可以将${\lambda }_t{\nabla }_{x_t}R\left(x_t\right)$替换为阶跃相关的先验函数${\lambda }_t{\nabla }_{x_t}R\left(x_t,t\right)$来平衡真实性和数据一致性，如Chen等人(2018)所示：
$$x_{t-1}=\left(x_t-{\lambda }_t{\nabla }_{x_t}R\left(x_t,t\right)\right)-ϵ{\nabla }_{x_t}\mathcal{U}\left(\mathbf{A}{x}_t,y\right).\text{\hspace{1em}(9)}$$
正如Song等人(2021)所证明的，分数函数是表示概率分布的强大工具。分数函数不需要计算可处理的归一化常数或其近似值。这使得使用分数函数估计$\log p(x)$成为可能。通过将先验项${\lambda }_t{\nabla }_{x_t}R\left(x_t,t\right)$替换为分数函数${\nabla }_x\log p_t\left(x\right)$，可以保证新的先验项不需要大量的计算就能准确地表示概率分布：
$$x_{t-1}=\left(x_t-{\lambda }_t{\nabla }_x\log p_t\left(x\right)\right)-ϵ{\nabla }_{x_t}\mathcal{U}\left(\mathbf{A}{x}_t,y\right),\text{\hspace{1em}(10)}$$
在公式(4)中，我们可以使用分数模型$s_{\theta }(x_t,t)$来近似${\nabla }_x\log p_t\left(x\right)$，使用分数匹配技术：
$$x_{t-1}\simeq \left(x_t-{\lambda }_t{s}_{\theta }\left(x_t,t\right)\right)-ϵ{\nabla }_{x_t}\mathcal{U}\left(\mathbf{A}{x}_t,y\right).\text{\hspace{1em}(11)}$$
事实上，第一项$x_t-{\lambda }_t{s}_{\theta }\left(x_t,t\right)$是具有无噪声约束的公式(3)。因此，我们可以放松无噪声约束，使用公式(3)来替换这一项：
$$x_{t-1}\simeq x_t-\underset{\text{Prior term}}{\left({\lambda }_t{s}_{\theta }\left(x_t,t\right)-g\left(t\right)z\right)}-\underset{\text{Data-fidelity term}}{ϵ{\nabla }_{x_t}\mathcal{U}\left(\mathbf{A}{x}_t,y\right)},z\sim \mathcal{N}\left(0,\mathbf{I}\right).\text{\hspace{1em}(12)}$$
提出了一种新的迭代重建方法——扩散迭代重建(Diffusion iterative reconstruction, DIR)。该模型使用分数模型来表示原始数据分布，并将其作为学习先验。算法1演示了DIR的像素引导过程。

值得注意的是，我们的DIR具有与Chung等人(2023b)提出的方法相似的数学形式。然而，我们的方法更通用，可以应用于更广泛的场景。扩散后验抽样(DPS) Chung等人(2023b)将数据一致性项$\mathcal{U}(\cdot ,\cdot )$建模为噪声测量问题。数据保真度项的评估函数是基于噪声分布的先验假设(如高斯噪声的L2函数)导出的。当测量过程中噪声类型已知时，这种方法效果良好。然而，在实际应用中，如何估计噪声分布并推导出正确的评价函数是一个挑战。相比之下，我们的DIR将数据保真度项建模为质量评估函数，而没有对噪声分布进行任何假设。因此，评价函数$\mathcal{U}(\cdot ,\cdot )$可以是任意可微的评价函数，具有更大的灵活性。

3.2 历史梯度更新

接下来，我们将展示引入历史梯度更新策略可以提供更好的重建结果。公式12)中梯度引导的基本公式对应于一个简单的梯度下降方案。指导率λ可以被认为是随机梯度下降(SGD)中的学习率值。因此，为了进一步提高数据的一致性，我们采用了前面步骤中的梯度信息。因为历史梯度信息可以提供样本级信息来决定制导过程的优化方向。这也被称为一阶基于梯度的优化。在这里，我们展示了基于两个典型优化器的梯度更新策略的两个变体。

类动量梯度更新策略。类似于动量优化器Sutskever等人(2013)，我们考虑使用梯度${\nabla }_{x_t}\mathcal{U}\left(\mathbf{A}{x}_t,y\right)$的移动平均$m^t$来执行梯度下降：
$$\begin{array}{rl}{m}^t& =\eta m^{t-1}+\left(1-\eta \right){\nabla }_{x_t}\mathcal{U}\left(\mathbf{A}{x}_t,y\right),\\ x_{t-1}& =x_t-ϵm^t,\end{array}\text{\hspace{1em}(13)(14)}$$
其中$\eta$是调节动量因子的超参数。

类Adam梯度更新策略。Adam优化器Kingma, Ba(2014)使用动量和自适应学习率来执行梯度下降：
$$\begin{array}{rl}{m}^t& ={\eta }_1{m}^{t-1}+\left(1-{\eta }_1\right){\nabla }_{x_t}\mathcal{U}\left(\mathbf{A}{x}_t,y\right),\\ v^t& ={\eta }_2{v}^{t-1}+\left(1-{\eta }_2\right){\nabla }_{x_t}\mathcal{U}{\left(\mathbf{A}{x}_t,y\right)}^2,\\ x_{t-1}& =x_t-ϵ\frac{{\hat{m}}^t}{\sqrt{{\hat{v}}^t}+\epsilon },\end{array}\text{\hspace{1em}(15)(16)(17)}$$
其中$({\eta }_1,{\eta }_2)$是用于计算梯度指数加权移动平均及其平方的系数，$ϵ$有助于提高数值稳定性。在移动平均线mt和vt的帮助下，我们可以有效地定位平坦最小值。

值得注意的是，$ϵ$和梯度策略的选择取决于评估函数$\mathcal{U}$(详细信息和消融研究见附录C)。我们的梯度更新策略是兼容的DIR, LDIR，和DPS是否在像素空间或潜在空间。这些细节在消融研究中得到证实。采用上述梯度更新策略的LDIR算法详情见附录A。

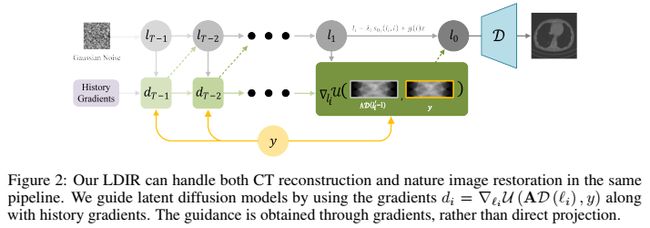
3.3 潜在扩散迭代重建

我们回顾了以前关于基于扩散的数据重建的工作，包括Chung等人(2023b, 2022, 2023a,c);Song et al . (2022);Wang et al .(2023)揭示了它们都是在像素空间中进行重建，这需要大量的计算资源。为了解决这一限制，我们从Rombach等人(2022)和我们的研究所提出的潜在扩散模型(LDM)中汲取灵感。本文提出了一种新的数据重建扩散模型——潜在扩散迭代重建(LDIR)。与以前的方法相比，LDIR有几个优点：(i)我们将图像编码到低维潜在空间中，而不是在像素空间中处理图像，使我们能够以更少的计算需求更有效地处理图像。(ii)与像素空间相比，潜在空间包含明显更高的信息密度，使我们能够纳入自然先验，如稀疏性，并提高恢复数据的质量。

从像素到潜在空间。为了将像素编码为潜在，我们构建了一个由编码器E和解码器D组成的自编码器，具体来说，在像素空间中给定一个输入图像$x$, $\mathcal{E}$将$x$映射到一个低维潜在向量$\ell =\mathcal{E}\left(x\right)$， $\mathcal{D}$从$\ell$重建图像$\bar{x}=\mathcal{D}\left(\mathcal{E}\left(x\right)\right)$。为了结合$x$的稀疏性先验，我们使用了Kingma, Welling(2013)提出的矢量量化变分自编码器(VQ-VAE);Rezende et al (2014);Esser等人(2021)与Van Den Oord等人(2017)的量化层。

潜在分数匹配。有了我们的语义压缩模型$\mathcal{E}$和$\mathcal{D}$，我们现在可以建立潜函数的分数${\nabla }_{\ell }\log p_t\left(\ell \right)$，并使用分数模型$s_{{\theta }_{\ell }}$来近似它，目标如下：
min ⁡ θ E t ∈ [ 0 , … , T − 1 ] , ℓ 0 ∼ p t , ℓ t ∼ p 0 ∣ t ( ℓ t ∣ ℓ 0 ) [ ∣ ∣ s θ ℓ ( ℓ , t ) − ∇ ℓ log ⁡ p 0 ∣ t ( ℓ t ∣ ℓ 0 ) ∣ ∣ ∣ 2 2 ] , (18) \left.\min_{\theta}\mathbb{E}_{t\in[0,\ldots,T-1],\ell_{0}\sim p_{t},\ell_{t}\sim p_{0|t}(\ell_{t}|\ell_{0})}\left[\left|\left|s_{\theta_{\ell}}\left(\ell,t\right)-\nabla_{\ell}\log p_{0|t}\left(\ell_{t}|\ell_{0}\right)\right|\right|\right|_{2}^{2}\right], \tag{18} θmin​Et∈[0,…,T−1],ℓ0​∼pt​,ℓt​∼p0∣t​(ℓt​∣ℓ0​)​[ ​ ​sθℓ​​(ℓ,t)−∇ℓ​logp0∣t​(ℓt​∣ℓ0​) ​ ​ ​22​],(18)
其中$p(\ell )=p(\mathcal{E}(x))$和$x\sim p(x)$。

条件引导过程上的潜在空间。与像素空间中的条件引导过程类似，我们首先使用分数模型$s_{{\theta }_{\ell }}$从标准高斯噪声中生成潜在特征：
$${\ell }_{t-1}^{\prime }={\ell }_t-f\left(\ell ,t\right)-g{\left(t\right)}^2{s}_{g_{ϵ}}\left(\ell ,t\right)+g\left(t\right)z,z\sim \mathcal{N}\left(0,\mathbf{I}\right),\text{\hspace{1em}(19)}$$
我们需要用$\mathcal{D}$将$\ell$解码到像素空间，并计算数据一致性项$\mathcal{U}(\mathbf{A}\mathcal{D}\left(\ell \right),y)$，可导出为：
$${\ell }_{t-1}={\ell }_{t-1}^{\prime }-ϵ{\nabla }_{{\ell }_t}\mathcal{U}\left(\mathbf{A}\mathcal{D}\left({\ell }_t\right),y\right)\text{\hspace{1em}(20)}$$
因此，我们可以得到LDIR的条件引导算法为：
$${\ell }_{t-1}\simeq {\ell }_t-\underset{\text{Prior term}}{\left({\lambda }_t{s}_{{\theta }_{\ell }}\left({\ell }_t,t\right)-g\left(t\right)z\right)}-\underset{\text{Data-fidelity term}}{ϵ{\nabla }_{{\ell }_{\ell }}\mathcal{U}\left(\mathbf{AD}\left({\ell }_t\right),y\right)},z\sim \mathcal{N}\left(0,\mathbf{I}\right)\text{\hspace{1em}(21)}$$
利用解码器$\mathcal{D}$对最终潜在信号$x_0=\mathcal{D}({\ell }_0)$进行解码即可得到最终结果。

4 Experiments

4.1 实验设置

模型和数据集。对于医学图像重建，我们在2016年美国医学物理学家协会(AAPM)大挑战数据集上训练了我们的DDPM和LDM模型。该数据集有来自10名患者的正常剂量数据。9个患者数据用于训练，1个用于验证，其中包含526张图像。为了模拟低剂量成像，采用了180度平行光束成像几何形状。关于喷漆和超分辨率任务，我们在CelebAHQ 1k 256 × 256数据集Liu et al(2015)和LSUN-bedroom 256 × 256数据集Yu et al(2015)上测试了我们的方法。我们使用来自Ho等人(2020)的开源模型存储库的预训练DDPM和LDM模型;Rombach et al .(2022)。所有图像归一化到范围[0,1]。包括超参数在内的更多细节列在附录中B。

测量操作符。对于稀疏视图CT重建，我们统一采样18和32个视图。对于有限角度CT重建，我们使用平行光束几何结构将成像度范围限制在45度和90度，128个视图。对于随机绘制，遵循Chung等人(2022,2023b)，我们屏蔽掉了总像素的99%(包括所有通道)。对于超分辨率，我们使用8×双线性下采样。在对自然图像进行前向运算后，加入高斯噪声进行评价。对医疗数据进行了无噪声评估。

4.2 医学数据评价

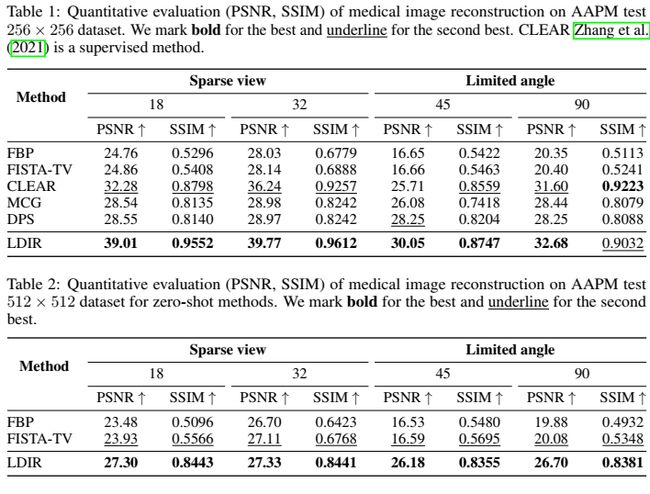
为了评估LDIR在重建医疗稀疏数据方面的性能，我们将其与几种最新的最先进的方法进行了比较:流形约束梯度(MCG) Chung等人(2022)，扩散后向抽样(DPS) Chung等人(2023b)，综合学习支持的对抗重建(CLEAR) Zhang等人(2021)，全变分快速迭代收缩阈值算法(FISTA-TV)，以及分析重建方法，滤波后投影(FBP)。采用峰值信噪比(PSNR)和结构相似度指标(SSIM)进行定量评价。

医学稀疏数据重建的定量结果如表1和表2所示。

我们的方法在所有实验设置中都明显优于所有其他最先进的方法。我们还比较了该方法在高分辨率CT图像重建任务中的应用。然而，由于 DDPM 的内存消耗较大，训练 DDPM 模型进行高分辨率重建具有挑战性。因此，我们从表2中排除了依赖于DDPM的MCG和DPS。结果表明，尽管重建图像与地面真实值之间仍有较大差距，但LDIR提供了无噪声的重建结果。相比之下，其他zero-shot方法无法重建有意义的结果。

医学稀疏图像重建的定性结果如图3所示，与表1所示的定量结果一致。

在图3中，我们将我们的方法与最先进的zero-shot无监督和监督方法进行了比较。实验结果表明，该方法能够提供高质量的图像重建，特别是对于稀疏视图重建任务。具体来说，LDIR可以提供更好的整体结构和几乎无伪影的重建。此外，在有限角度重建任务中，我们的方法也提供了比其他方法更好的重建。(更多医学稀疏数据重构的定性结果见附录D)。

4.3 自然图像评价

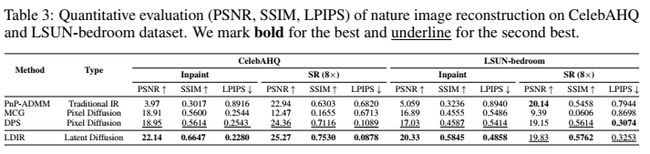
为了进一步测试我们的方法的性能，我们将我们的方法与最先进的方法进行了比较，即MCG, DPS和即插即用的乘法器交替方向方法(PnP-ADMM) Chan等人(2016)。为了进行定量分析，我们使用了三种广泛使用的感知评估指标：LPIPS距离、PSNR和SSIM。

自然图像重建定量结果如表3所示。

我们的方法与以前的先进技术相比取得了具有竞争力的结果。具体来说，我们观察到我们的方法能够准确地重建原始数据并保持最大的数据一致性，即使在处理高度稀疏的测量时，如99%随机绘制。此外，我们注意到LDIR在超分辨率任务上比以前的最佳方法有一些优势。

自然稀疏图像重建的定性结果如图4所示。

值得注意的是，传统的迭代方法PnP-ADMM由于其先验项的限制，在图像补全和超分辨率任务上都不能产生令人满意的结果。相比之下，我们的方法优于比较方法，特别是在油漆任务中的颜色和结构方面。在超分辨率任务中，MCG获得的结果显示出许多伪影，这可能是由于投影步骤 chung et al (2023b)。另一方面，我们的方法与最先进的方法 DPS 取得了有竞争力的结果，但差距很小。(更多的自然稀疏图像重构定性结果见附录E)。

4.4 消融研究

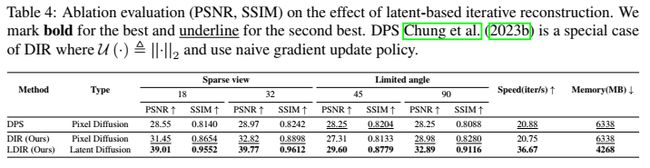
我们进行了消融研究来验证我们方法的有效性。我们比较了基于潜在的迭代重建方法和基于像素的迭代重建方法的性能。为了确保公平的比较，我们对医学图像重建任务进行了这些消融研究，因为DDPM和LDM模型都使用相同的协议进行训练。

在表4中，我们可以观察到我们的LDIR在很大程度上优于基于像素的迭代重建方法DPS和DIR。这一结果证实了基于潜在的方法在速度和精度方面都优于基于像素的方法。此外，我们可以看到，将评估函数更改为L1并在像素空间中使用类似动量的梯度更新策略可以提高DIR的性能，使其超过DPS。与像素空间模型相比，LDIR以更少的内存消耗实现了显著的加速。尽管LDIR在每一步都将潜信号解码成图像，但它仍然比直接在像素空间中处理具有更大的优势。

5 Conclusion

在本文中，我们提出了潜在扩散迭代重建(LDIR)作为一种新的方法来重建CT稀疏数据的zero-shot方式。我们从理论上证明，利用潜在扩散模型作为先验项可以忽略成对数据的依赖项。此外，我们在潜在空间而不是像素空间中生成先验项，这有助于我们以更低的计算复杂度和采样时间形成高分辨率图像。利用数据保真项的样本级历史梯度信息，可以在潜在空间中指导重建过程。我们的实验结果表明，LDIR在稀疏CT数据重建上优于监督方法等先进方法，在自然图像恢复上取得了具有竞争力的结果。我们相信，我们的工作为利用快速发展的潜在扩散模型领域提供了一个有前途的工具，可以从退化的测量中恢复高质量和高分辨率的数据。

Appendix

没找到