数据结构基础：P10.3-排序(二)---＞基数排序

本系列文章为浙江大学陈越、何钦铭数据结构学习笔记，前面的系列文章链接如下：
数据结构基础：P1-基本概念
数据结构基础：P2.1-线性结构—＞线性表
数据结构基础：P2.2-线性结构—＞堆栈
数据结构基础：P2.3-线性结构—＞队列
数据结构基础：P2.4-线性结构—＞应用实例：多项式加法运算
数据结构基础：P2.5-线性结构—＞应用实例：多项式乘法与加法运算-C实现
数据结构基础：P3.1-树(一)—＞树与树的表示
数据结构基础：P3.2-树(一)—＞二叉树及存储结构
数据结构基础：P3.3-树(一)—＞二叉树的遍历
数据结构基础：P3.4-树(一)—＞小白专场：树的同构-C语言实现
数据结构基础：P4.1-树(二)—＞二叉搜索树
数据结构基础：P4.2-树(二)—＞二叉平衡树
数据结构基础：P4.3-树(二)—＞小白专场：是否同一棵二叉搜索树-C实现
数据结构基础：P4.4-树(二)—＞线性结构之习题选讲：逆转链表
数据结构基础：P5.1-树(三)—＞堆
数据结构基础：P5.2-树(三)—＞哈夫曼树与哈夫曼编码
数据结构基础：P5.3-树(三)—＞集合及运算
数据结构基础：P5.4-树(三)—＞入门专场：堆中的路径
数据结构基础：P5.5-树(三)—＞入门专场：File Transfer
数据结构基础：P6.1-图(一)—＞什么是图
数据结构基础：P6.2-图(一)—＞图的遍历
数据结构基础：P6.3-图(一)—＞应用实例：拯救007
数据结构基础：P6.4-图(一)—＞应用实例：六度空间
数据结构基础：P6.5-图(一)—＞小白专场：如何建立图-C语言实现
数据结构基础：P7.1-图(二)—＞树之习题选讲：Tree Traversals Again
数据结构基础：P7.2-图(二)—＞树之习题选讲：Complete Binary Search Tree
数据结构基础：P7.3-图(二)—＞树之习题选讲：Huffman Codes
数据结构基础：P7.4-图(二)—＞最短路径问题
数据结构基础：P7.5-图(二)—＞哈利·波特的考试
数据结构基础：P8.1-图(三)—＞最小生成树问题
数据结构基础：P8.2-图(三)—＞拓扑排序
数据结构基础：P8.3-图(三)—＞图之习题选讲-旅游规划
数据结构基础：P9.1-排序(一)—＞简单排序(冒泡、插入)
数据结构基础：P9.2-排序(一)—＞希尔排序
数据结构基础：P9.3-排序(一)—＞堆排序
数据结构基础：P9.4-排序(一)—＞归并排序
数据结构基础：P10.1-排序(二)—＞快速排序
数据结构基础：P10.2-排序(二)—＞表排序

---

前言

前面我们讲了那么多排序算法，它们有一个共同的特点：他们仅仅是基于比较大小来决定元素位置的。那么有定理结论告诉我们，仅仅基于比较进行的排序算法它们的最坏时间复杂度下界是$\mathrm{O}(\mathrm{N}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{N})$。也就是说，我们总能制造出一个最坏情况让它用最快的算法跑，它也只能跑到NlogN。那么还有没有可能更快呢？当然有可能！就是我们除了比较之外还干点什么别的事，这就是基数排序

一、桶排序

在介绍基数排序之前，我们先来看一下桶排序，事实上基数排序是桶排序的升级版。

例子

题目：假设我们有N个学生，他们的成绩是0到100之间的整数(于是有M=101个不同的成绩值) 。如何在线性时间内将学生按成绩排序？
解决思路：
①我们为每一个成绩值构造一个桶，于是我就建了101个桶。换言之我就是在程序里面设了一个数组count，这个数组的每一个元素是一个指针，它一开始被初始化为一个空链表的头指针，所以我们一开始有了101个空链表，也就对应了101个空的桶。

②当第i个学生进来的时候，比如说有一个学生考了88分，我们就先找到88这个桶，然后把这个学生的信息插到这个链表的表头里。

算法对应伪码如下：

void Bucket_Sort(ElementType A[], int N) 
{ 
	count[]初始化;
	while (读入1个学生成绩grade)
		将该生插入count[grade]链表;
	for ( i=0; i<M; i++ ) {
		if ( count[ ( count[i] )
			输出整个count[i]链表;
	} 
}

时间复杂度

$\mathrm{T}(\mathrm{N},\mathrm{M})=\mathrm{O}(\mathrm{M}+\mathrm{N})$
①在插入的时候，因为每一次我都插到表头，所以是一个常数倍的时间。我把N个学生的信息逐个插到相应的表里去，那就是一个$\mathrm{O}(\mathrm{N})$的时间。我输出的时候，我还需要扫描每一个桶，这一共有M个桶，所以还要加上M的时间。所以是$\mathrm{O}(\mathrm{M}+\mathrm{N})$
②当M非常小的时候，比如说有4万个学生，只有101个不同成绩值的时候，那这个其实就是一种线性的算法了。

二、基数排序

对于上面那个例子，我们有一个问题：如果M要比N要大很多，该怎么办呢？

例子

题目：假设我们有N=10个整数，每个整数的值在0到999之间(于是有M=1000个不同的值)。还有可能在线性时间内排序吗？
解决思路：
这N个整数最大就是三位数，并且它们是十进制，基数就是10，利用这些特征我们来建桶。
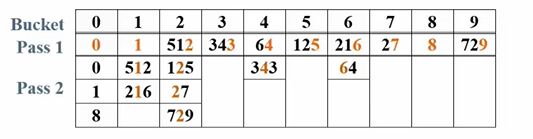
假设现在我们输入的10个数是：64, 8, 216, 512, 27, 729, 0, 1, 343, 125
我们用次位优先(Least Significant Digit)的思想来排序，即根据最低位的大小来排序，比如216和27，我们认为27的次位大于216的次位。
①首先，基数为10，建立10个桶

②在第一趟排序的时候，我们按照它们的个位数把它们放到相应的桶里去

③在第二趟排序的时候，我们按照它们的十位数把它们放到相应的桶里去

④在第三趟排序的时候，我们按照它们的百位数把它们放到相应的桶里去

⑤我们将所有的桶从前到后串在一起，就得到：0,1,8,27,64,125,216,343,512,729。整个数列就是有序的了。

时间复杂度：

$\mathrm{T}=\mathrm{O}(\mathrm{P}(\mathrm{N}+\mathrm{B}))$
我们一共经历了P趟排序，在每一趟排序里面我首先要把N个数全部都收集起来并分配一遍。收集分配的过程跟桶的个数是有关系的，至少要访问建立的B个桶。所以整体复杂度是：P(N+B)。当桶的个数非常小的话，基本是线性复杂度，比正常的排序效果好。

三、多关键字的排序

基数排序不仅仅是用于处理整数的基数排序，它还可以被用于处理有多关键字的排序。

例子

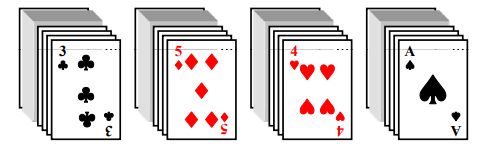
一副扑克牌就是按两种关键字来排序的，主关键字叫做花色，次关键字是面值。新牌拿到手的时候，就是按照下面的顺序排列的。基数排序在处理多关键字排序的时候，实际上可以每一种关键字理解成为那个整数里面的某一位。比如说次关键字就对应的是它的个位，主关键字就对应的是它的高位。那我有两种排序方法：主位优先和次位优先。

①我们根据主位优先(Most Significant Digit First)来建立桶，于是就把50多张牌往对应花色桶里面放。

②然后我们在每一个桶里进行排序，将数值顺序调整正确，最后来合并结果。
问题：我们还是需要在每个桶里面调用相应的排序算法来解决面值的排序，但是总体的时间复杂度一般来说会比你把它完整的看成一个待排数组来排要稍微好一点。但是，显然这个主位优先在这里面这么排不是很聪明。

使用次位优先

①根据面值建立13个桶
②然后把这50多张牌分别往这个13个桶里面丢，每个桶对应的是一种面值

③我下一步只要把结果合并起来，然后再为花色建四个桶。接着，我根本不需要排序，只需要从上到下把这些牌按照它的花色
放到相应的花色的桶里面去，最后再收集一下，把结果一合并就得到了我们最后有序的序列。

C语言代码：基数排序-次位优先

/* 基数排序 - 次位优先 */

/* 假设元素最多有MaxDigit个关键字，基数全是同样的Radix */
#define MaxDigit 4
#define Radix 10

/* 桶元素结点 */
typedef struct Node *PtrToNode;
struct Node {
    int key;
    PtrToNode next;
};

/* 桶头结点 */
struct HeadNode {
    PtrToNode head, tail;
};
typedef struct HeadNode Bucket[Radix];
 
int GetDigit ( int X, int D )
{ /* 默认次位D=1, 主位D<=MaxDigit */
    int d, i;
    
    for (i=1; i<=D; i++) {
        d = X % Radix;
        X /= Radix;
    }
    return d;
}

void LSDRadixSort( ElementType A[], int N )
{ /* 基数排序 - 次位优先 */
     int D, Di, i;
     Bucket B;
     PtrToNode tmp, p, List = NULL; 
     
     for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */
         B[i].head = B[i].tail = NULL;
     for (i=0; i<N; i++) { /* 将原始序列逆序存入初始链表List */
         tmp = (PtrToNode)malloc(sizeof(struct Node));
         tmp->key = A[i];
         tmp->next = List;
         List = tmp;
     }
     /* 下面开始排序 */ 
     for (D=1; D<=MaxDigit; D++) { /* 对数据的每一位循环处理 */
         /* 下面是分配的过程 */
         p = List;
         while (p) {
             Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */
             /* 从List中摘除 */
             tmp = p; p = p->next;
             /* 插入B[Di]号桶尾 */
             tmp->next = NULL;
             if (B[Di].head == NULL)
                 B[Di].head = B[Di].tail = tmp;
             else {
                 B[Di].tail->next = tmp;
                 B[Di].tail = tmp;
             }
         }
         /* 下面是收集的过程 */
         List = NULL; 
         for (Di=Radix-1; Di>=0; Di--) { /* 将每个桶的元素顺序收集入List */
             if (B[Di].head) { /* 如果桶不为空 */
                 /* 整桶插入List表头 */
                 B[Di].tail->next = List;
                 List = B[Di].head;
                 B[Di].head = B[Di].tail = NULL; /* 清空桶 */
             }
         }
     }
     /* 将List倒入A[]并释放空间 */
     for (i=0; i<N; i++) {
        tmp = List;
        List = List->next;
        A[i] = tmp->key;
        free(tmp);
     } 
}

C语言代码：基数排序-主位优先

* 基数排序 - 主位优先 */

/* 假设元素最多有MaxDigit个关键字，基数全是同样的Radix */

#define MaxDigit 4
#define Radix 10

/* 桶元素结点 */
typedef struct Node *PtrToNode;
struct Node{
    int key;
    PtrToNode next;
};

/* 桶头结点 */
struct HeadNode {
    PtrToNode head, tail;
};
typedef struct HeadNode Bucket[Radix];
 
int GetDigit ( int X, int D )
{ /* 默认次位D=1, 主位D<=MaxDigit */
    int d, i;
    
    for (i=1; i<=D; i++) {
        d = X%Radix;
        X /= Radix;
    }
    return d;
}

void MSD( ElementType A[], int L, int R, int D )
{ /* 核心递归函数: 对A[L]...A[R]的第D位数进行排序 */
     int Di, i, j;
     Bucket B;
     PtrToNode tmp, p, List = NULL; 
     if (D==0) return; /* 递归终止条件 */
     
     for (i=0; i<Radix; i++) /* 初始化每个桶为空链表 */
         B[i].head = B[i].tail = NULL;
     for (i=L; i<=R; i++) { /* 将原始序列逆序存入初始链表List */
         tmp = (PtrToNode)malloc(sizeof(struct Node));
         tmp->key = A[i];
         tmp->next = List;
         List = tmp;
     }
     /* 下面是分配的过程 */
     p = List;
     while (p) {
         Di = GetDigit(p->key, D); /* 获得当前元素的当前位数字 */
         /* 从List中摘除 */
         tmp = p; p = p->next;
         /* 插入B[Di]号桶 */
         if (B[Di].head == NULL) B[Di].tail = tmp;
         tmp->next = B[Di].head;
         B[Di].head = tmp;
     }
     /* 下面是收集的过程 */
     i = j = L; /* i, j记录当前要处理的A[]的左右端下标 */
     for (Di=0; Di<Radix; Di++) { /* 对于每个桶 */
         if (B[Di].head) { /* 将非空的桶整桶倒入A[], 递归排序 */
             p = B[Di].head;
             while (p) {
                 tmp = p;
                 p = p->next;
                 A[j++] = tmp->key;
                 free(tmp);
             }
             /* 递归对该桶数据排序, 位数减1 */
             MSD(A, i, j-1, D-1);
             i = j; /* 为下一个桶对应的A[]左端 */
         } 
     } 
}

void MSDRadixSort( ElementType A[], int N )
{ /* 统一接口 */
    MSD(A, 0, N-1, MaxDigit); 
}

小测验

1、基数排序是稳定的算法 (正确)