Python 密码破解指南：20~24

协议：CC BY-NC-SA 4.0

译者：飞龙

本文来自【OpenDocCN 饱和式翻译计划】，采用译后编辑（MTPE）流程来尽可能提升效率。

收割 SB 的人会被 SB 们封神，试图唤醒 SB 的人是 SB 眼中的 SB。——SB 第三定律

二十、破解维吉尼亚密码

原文：https://inventwithpython.com/cracking/chapter20.html

“隐私权是一项与生俱来的人权，是维护人类尊严和尊重的必要条件。”

——布鲁斯·施奈尔，密码学家，2006 年

有两种方法可以破解维吉尼亚密码。一种方法使用强力字典攻击来尝试将字典文件中的每个单词作为维吉尼亚密钥，只有当该密钥是英语单词时才有效，如 RAVEN 或 DESK。第二种更复杂的方法是 19 世纪数学家查尔斯·巴贝奇使用的，即使密钥是一组随机的字母，如 VUWFE 或 PNFJ，它也能工作。在本章中，我们将使用这两种方法编写程序来破解维吉尼亚密码。

本章涵盖的主题

• 字典攻击

• 卡西斯基检查

• 计算因数

• set数据类型和set()函数

• extend()列表方法

• itertools.product()函数

使用字典攻击暴力破解维吉尼亚密码

我们将首先使用字典攻击来破解维吉尼亚密码。字典文件dictionary.txt （可在本书网站www.nostarch.com/crackingcodes）约有 45000 个英语单词。我的电脑只需不到五分钟就能完成对一个长段落大小的信息的所有解密。这意味着，如果使用一个英语单词来加密一个维吉尼亚密文，该密文容易受到字典攻击。让我们来看一个使用字典攻击来破解维吉尼亚密码的程序的源代码。*

维吉尼亚字典破解程序的源代码

选择文件 -> 新文件，打开新文件编辑器窗口。在文件编辑器中输入以下代码，然后保存为vigeneredictionaryhacker.py。确保将detectEnglish.py、vigenereCipher.py和pyperclip.py文件与vigeneredictionaryhacker.py文件放在同一目录下。然后按F5运行程序。

守护
字典
黑客. py

# Vigenere Cipher Dictionary Hacker
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)

import detectEnglish, vigenereCipher, pyperclip

def main():
    ciphertext = """Tzx isnz eccjxkg nfq lol mys bbqq I lxcz."""
    hackedMessage = hackVigenereDictionary(ciphertext)

    if hackedMessage != None:
        print('Copying hacked message to clipboard:')
        print(hackedMessage)
        pyperclip.copy(hackedMessage)
    else:
        print('Failed to hack encryption.')


def hackVigenereDictionary(ciphertext):
    fo = open('dictionary.txt')
    words = fo.readlines()
    fo.close()

    for word in lines:
        word = word.strip() # Remove the newline at the end.
        decryptedText = vigenereCipher.decryptMessage(word, ciphertext)
        if detectEnglish.isEnglish(decryptedText, wordPercentage=40):
            # Check with user to see if the decrypted key has been found:
            print()
            print('Possible encryption break:')
            print('Key ' + str(word) + ': ' + decryptedText[:100])
            print()
            print('Enter D for done, or just press Enter to continue
                  breaking:')
            response = input('> ')

            if response.upper().startswith('D'):
                return decryptedText

if __name__ == '__main__':
    main()

维吉尼亚字典破解程序的运行示例

当您运行vigeneredictionaryhacker.py程序时，输出应该是这样的:

Possible encryption break:
Key ASTROLOGY: The recl yecrets crk not the qnks I tell.
Enter D for done, or just press Enter to continue breaking:
>
Possible encryption break:
Key ASTRONOMY: The real secrets are not the ones I tell.
Enter D for done, or just press Enter to continue breaking:
> d
Copying hacked message to clipboard:
The real secrets are not the ones I tell.

程序建议的第一个关键字（ASTROLOGY）不起作用，所以用户按Enter让破解程序继续，直到找到正确的解密密钥（ASTRONOMY）。

关于维吉尼亚字典破解程序

因为vigeneredictionaryhacker.py程序的源代码与本书中之前的破解程序类似，所以我不会逐行解释。简单来说，hackVigenereDictionary()函数试图使用字典文件中的每个单词来解密密文，当解密后的文本看起来像英语时（根据detectEnglish模块），它打印解密并提示用户退出或继续。

注意，这个程序对从open()返回的文件对象使用了readlines()方法:

    words = fo.readlines()

与将文件的全部内容作为单个字符串返回的read()方法不同，readlines()方法返回一个字符串列表，其中每个字符串是文件中的一行。因为字典文件的每一行都有一个单词，所以words变量包含了从Aarhus到Zurich的每一个英语单词的列表。

程序的其余部分，从第 23 行到第 36 行，类似于第 12 章中的换位密码破解程序。一个for循环将迭代words列表中的每个单词，以单词为密钥解密消息，然后调用detectEnglish.isEnglish()查看结果是否是可理解的英文文本。

现在，我们已经编写了一个使用字典攻击来破解维吉尼亚密码的程序，让我们看看如何破解维吉尼亚密码，即使密钥是一组随机的字母而不是字典中的单词。

使用卡西斯基检查来查找密钥的长度

卡西斯基检查是一个我们可以用来确定用于加密密文的维吉尼亚密钥长度的过程。然后，我们可以使用频率分析来单独破解每个子密钥。查尔斯·巴贝奇是第一个用这种方法破解维吉尼亚尔密码的人，但他从未公布过他的结果。他的方法后来被 20 世纪早期的数学家弗雷德里希·卡西斯基发表，他成为了这种方法的同名者。我们来看看卡西斯基考试涉及的步骤。这些是我们的维吉尼亚黑客程序将采取的步骤。

寻找重复序列

卡西斯基检查的第一步是找到密文中至少三个字母的每个重复集。这些重复的序列可以是使用维吉尼亚密钥的相同子密钥加密的相同明文字母。例如，如果你用密钥 SPILLTHEBEANS 加密明文，你会得到:

THECATISOUTOFTHEBAG
SPILLTHEBEANSSPILLT
LWMNLMPWPYTBXLWMMLZ

注意，字母LWM重复了两次。原因是在密文中，LWM是使用与密钥相同的字母（SPI）加密的明文，因为密钥恰好在第二次加密时重复。从第一个LWM开始到第二个LWM开始的字母数，我们称之为间距，是 13。这表明用于该密文的密钥有 13 个字母长。只要看看重复的序列，你就能算出密钥的长度。

然而，在大多数密文中，密钥不会方便地与重复的字母序列对齐，或者密钥可能在重复序列之间重复多次，这意味着重复字母之间的字母数量将等于密钥的倍数，而不是密钥本身。为了解决这些问题，让我们看一个更长的例子，在这个例子中，我们不知道密钥是什么。

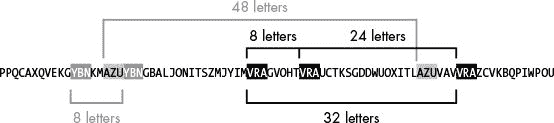
当我们去掉密文中的非字母PPQCA XQVEKG YBNKMAZU YBNGBAL JON I TSZM JYIM. VRAG VOHT VRAU C TKSG. DDWUO XITLAZU VAVV RAZ C VKB QP IWPOU，它看起来像图 20-1 所示的字符串。该图还显示了该字符串中的重复序列——VRA、AZU和YBN——以及每个序列对之间的字母数。

图 20-1：示例字符串中的重复序列

在这个例子中，有几个潜在的密钥长度。卡西斯基检查的下一步是计算这些计数的所有因数，以缩小潜在的密钥长度。

获取间隔因数

在示例中，序列之间的间隔是 8、8、24、32 和 48。但是间距的因数比间距更重要。

要了解原因，请看表 20-1 中的消息“密码”并尝试用九个字母的密钥ABCDEFGHI和三个字母的密钥XYZ对其加密。每个密钥在消息长度内重复。

表 20-1： 用两个不同的密钥加密密码

	用ABCDEFGHI加密	用XYZ加密
明文消息	DOGANDCAT	DOGANDCAT
密钥（重复）	ABCDEFGHIABCDEF	XYZXYZ
密文	TIGGSLGULTIGFEY	QFDAMFXLCZYS

正如所料，这两个密钥产生了两种不同的密文。当然，黑客不会知道原始消息或密钥，但他们会在TIGGSLGULTIGFEY密文中看到序列TIG出现在索引 0 和索引 9 处。因为9 – 0 = 9，这些序列之间的间距是 9，这似乎表明原始密钥是一个九个字母的密钥；在这种情况下，指示是正确。

然而，QFDAMFXLCQFDZYS密文也会产生一个重复序列（QFD），出现在索引 0 和索引 9 处。这些序列之间的间距也是 9，这表明该密文中使用的密钥也是 9 个字母长。但是我们知道密钥只有三个字母长:XYZ。

当消息中的相同字母（在我们的示例中为）用密钥中的相同字母（在我们的示例中为ABC和XYZ）加密时，会出现重复序列，这发生在消息和密钥中的相似字母“排列”并加密到相同序列时。这种对齐可以发生在任意倍数的真实密钥长度上（比如 3、6、9、12 等等），这就是为什么三个字母的密钥可以产生间隔为 9 的重复序列。

因此，可能的密钥长度不仅取决于间距，还取决于间距的任何因数。9 的因数是 9、3 和 1。因此，如果您发现间距为 9 的重复序列，您必须考虑密钥的长度可能是 9 或 3。我们可以忽略 1，因为只有一个字母密钥的维吉尼亚密码就是凯撒密码。

卡西斯基检验的第 2 步包括找出每个间距的因数（不包括 1），如表 20-2 所示。

表 20-2： 各间距的因数

间距	因数
8	2, 4, 8
24	2, 4, 6, 8, 12, 24
32	2, 4, 8, 16
48	2, 4, 6, 8, 12, 24, 48

数字 8、8、24、32 和 48 合起来有以下因数:2、2、2、2、4、4、4、6、6、8、8、8、12、12、16、24、24 和 48。

密钥很可能是最常出现的因数，你可以通过计数来确定。因为 2、4 和 8 是最常出现的间距因数，所以它们是最有可能的维吉尼亚调长度。

从字符串中每隔 N 个字母获取一个

现在我们有了维吉尼亚密钥的可能长度，我们可以使用这个信息一次解密一个子密钥。对于这个例子，让我们假设密钥长度是 4。如果我们不能破解这个密文，我们可以假设密钥长度为 2 或 8 再试一次。

因为密钥是循环加密明文的，所以密钥长度为 4 意味着从第一个字母开始，密文中的每四个字母使用第一个子密钥加密，从明文的第二个字母开始的每四个字母使用第二个子密钥加密，依此类推。使用这些信息，我们将从由同一个子密钥加密的字母的密文中形成字符串。首先，让我们确定如果我们从不同的字母开始，字符串中的第四个字母会是什么。然后我们将这些字母组合成一个字符串。在这些例子中，我们将每第四个字母加粗。

识别从第一个字母开始的每第四个字母:

PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLAZUVAVVRAZCV
KBQPIWPOU

接下来，我们找到从第二个字母开始的第四个字母:

PPQCAXQVEKGYBNKMAZUYBNGBALJONITSZMJYIMVRAGVOHTVRAUCTKSGDDWUOXITLAZUVAVVRAZCV
KBQPIWPOU

然后我们从第三个字母和第四个字母开始做同样的事情，直到我们达到我们正在测试的子密钥的长度。表 20-3 显示了每次迭代的粗体字母组合字符串。

表 20-3： 每隔四个字母的字符串

起始	字符串
第一个字母	PAEBABANZIAHAKDXAAAKIU
第二个字母	PXKNZNLIMMGTUSWIZVZBW
第三个字母	QQGKUGJTJVVVCGUTUVCQP
第四个字母	CVYMYBOSYRORTDOLVRVPO

利用频率分析破解每个子密钥

如果我们猜测了正确的密钥长度，那么我们在上一节中创建的四个字符串中的每一个都将使用一个子密钥进行加密。这意味着当用正确的子密钥解密字符串并进行频率分析时，解密的字母很可能具有高的英语频率匹配分数。以第一个字符串PAEBABANZIAHAKDXAAAKIU为例，让我们看看这个过程是如何工作的。

首先，我们使用第 18 章、vigenereCipher.decryptMessage()中的维吉尼亚解密函数对字符串解密 26 次（26 个可能的子密钥中的每一个一次）。然后我们使用第 19 章、freqAnalysis.、englishFreqMatchScore、()中的英文频率分析函数测试每个解密的字符串。在交互式 shell 中运行以下代码:

>>> import freqAnalysis, vigenereCipher
>>> for subkey in 'ABCDEFGHJIJKLMNOPQRSTUVWXYZ':
...   decryptedMessage = vigenereCipher.decryptMessage(subkey, 
        'PAEBABANZIAHAKDXAAAKIU')
...   print(subkey, decryptedMessage, 
        freqAnalysis.englishFreqMatchScore(decryptedMessage))
...
A PAEBABANZIAHAKDXAAAKIU 2
B OZDAZAZMYHZGZJCWZZZJHT 1
--snip--

表 20-4 显示了结果。

表 20-4： 每次解密的英文频率匹配得分

子密钥	解密	英语频率匹配分数
'A'	'PAEBABANZIAHAKDXAAAKIU'	2
'B'	'OZDAZAZMYHZGZJCWZZZJHT'	1
'C'	'NYCZYZYLXGYFYIBVYYYIGS'	1
'D'	'MXBYXYXKWFXEXHAUXXXHFR'	0
'E'	'LWAXWXWJVEWDWGZTWWWGEQ'	1
'F'	'KVZWVWVIUDVCVFYSVVVFDP'	0
'G'	'JUYVUVUHTCUBUEXRUUUECO'	1
'H'	'ITXUTUTGSBTATDWQTTTDBN'	1
'I'	'HSWTSTSFRASZSCVPSSSCAM'	2
'J'	'GRVSRSREQZRYRBUORRRBZL'	0
'K'	'FQURQRQDPYQXQATNQQQAYK'	1
'L'	'EPTQPQPCOXPWPZSMPPPZXJ'	0
'M'	'DOSPOPOBNWOVOYRLOOOYWI'	1
'N'	'CNRONONAMVNUNXQKNNNXVH'	2
'O'	'BMQNMNMZLUMTMWPJMMMWUG'	1
'P'	'ALPMLMLYKTLSLVOILLLVTF'	1
'Q'	'ZKOLKLKXJSKRKUNHKKKUSE'	0
'R'	'YJNKJKJWIRJQJTMGJJJTRD'	1
'S'	'XIMJIJIVHQIPISLFIIISQC'	1
'T'	'WHLIHIHUGPHOHRKEHHHRPB'	1
'U'	'VGKHGHGTFOGNGQJDGGGQOA'	1
'V'	'UFJGFGFSENFMFPICFFFPNZ'	1
'W'	'TEIFEFERDMELEOHBEEEOMY'	2
'X'	'SDHEDEDQCLDKDNGADDDNLX'	2
'Y'	'RCGDCDCPBKCJCMFZCCCMKW'	0
'Z'	'QBFCBCBOAJBIBLEYBBBLJV'	0

产生与英语最接近的频率匹配的解密的子密钥最有可能是真正的子密钥。在表 20-4 中，子项'A'、'I'、'N'、'W'和'X'导致第一串的最高频率匹配分数。请注意，这些分数通常很低，因为没有足够的密文来给我们一个大的文本示例，但对于这个例子来说，它们已经足够好了。

下一步是对其他三个字符串重复这个过程，以找到它们最可能的子项。表 20-5 显示了最终结果。

表 20-5： 最可能的子密钥为示例字符串

密文串	最有可能的子项
PAEBABANZIAHAKDXAAAKIU	A，I，N，W，X
PXKNZNLIMMGTUSWIZVZBW	I，Z
QQGKUGJTJVVVCGUTUVCQP	C
CVYMYBOSYRORTDOLVRVPO	K，N，R，V，Y

因为第一个子密钥有五个可能的子密钥，第二个子密钥有两个，第三个子密钥有一个，第四个子密钥有五个，所以组合的总数是 50（我们将所有可能的子密钥相乘得到5 × 2 × 1 × 5）。换句话说，我们需要暴力破解 50 个可能的密钥。但是这比暴力破解26 × 26 × 26 × 26（或 456,976）个可能的密钥要好得多，如果我们没有缩小可能的子项列表的话。如果维吉尼亚调更长，这种差异会变得更大！

暴力破解可能的密钥

为了暴力破解密钥，我们将尝试所有可能的子密钥组合。所有 50 种可能的子项组合如下所示:

我们的维吉尼亚破解程序的最后一步将是在完整的密文上测试所有 50 个解密密钥，看哪一个产生可读的英语明文。这样做应该可以揭示PPQCA XQVEKG…密文的密钥是WICK。

维吉尼亚破解程序的源代码

选择文件 -> 新文件，打开新文件编辑器窗口。确保detectEnglish.py、freqAnalysis.py、vigenereCipher.py和pyperclip.py文件与vigenereHacker.py文件在同一目录下。然后在文件编辑器中输入以下代码，保存为vigenereHacker.py。按F5运行程序。

这个程序中第 17 行的密文很难从书上复制。为了避免错别字，请从该书的网站www.nostarch.com/crackingcodes复制并粘贴。您可以使用本书网站上的在线比较工具来检查您的程序文本和本书中的程序文本之间的任何差异。

vigenereHacker.py

# Vigenere Cipher Hacker
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)

import itertools, re
import vigenereCipher, pyperclip, freqAnalysis, detectEnglish

LETTERS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
MAX_KEY_LENGTH = 16 # Will not attempt keys longer than this.
NUM_MOST_FREQ_LETTERS = 4 # Attempt this many letters per subkey.
SILENT_MODE = False # If set to True, program doesn't print anything.
NONLETTERS_PATTERN = re.compile('[^A-Z]')


def main():
    # Instead of typing this ciphertext out, you can copy & paste it
    # from https://www.nostarch.com/crackingcodes/:
    ciphertext = """Adiz Avtzqeci Tmzubb wsa m Pmilqev halpqavtakuoi,
           lgouqdaf, kdmktsvmztsl, izr xoexghzr kkusitaaf. Vz wsa twbhdg
           ubalmmzhdad qz
           --snip--
           azmtmd'g widt ion bwnafz tzm Tcpsw wr Zjrva ivdcz eaigd yzmbo
           Tmzubb a kbmhptgzk dvrvwz wa efiohzd."""
    hackedMessage = hackVigenere(ciphertext)

    if hackedMessage != None:
        print('Copying hacked message to clipboard:')
        print(hackedMessage)
        pyperclip.copy(hackedMessage)
    else:
        print('Failed to hack encryption.')


def findRepeatSequencesSpacings(message):
    # Goes through the message and finds any 3- to 5-letter sequences
    # that are repeated. Returns a dict with the keys of the sequence and
    # values of a list of spacings (num of letters between the repeats).

    # Use a regular expression to remove non-letters from the message:
    message = NONLETTERS_PATTERN.sub('', message.upper())

    # Compile a list of seqLen-letter sequences found in the message:
    seqSpacings = {} # Keys are sequences; values are lists of int spacings.
    for seqLen in range(3, 6):
        for seqStart in range(len(message) - seqLen):
            # Determine what the sequence is and store it in seq:
            seq = message[seqStart:seqStart + seqLen]

            # Look for this sequence in the rest of the message:
            for i in range(seqStart + seqLen, len(message) - seqLen):
                if message[i:i + seqLen] == seq:
                    # Found a repeated sequence:
                    if seq not in seqSpacings:
                        seqSpacings[seq] = [] # Initialize blank list.

                    # Append the spacing distance between the repeated
                    # sequence and the original sequence:
                    seqSpacings[seq].append(i - seqStart)
    return seqSpacings


def getUsefulFactors(num):
    # Returns a list of useful factors of num. By "useful" we mean factors
    # less than MAX_KEY_LENGTH + 1 and not 1\. For example,
    # getUsefulFactors(144) returns [2, 3, 4, 6, 8, 9, 12, 16].

    if num < 2:
        return [] # Numbers less than 2 have no useful factors.

    factors = [] # The list of factors found.

    # When finding factors, you only need to check the integers up to
    # MAX_KEY_LENGTH:
    for i in range(2, MAX_KEY_LENGTH + 1): # Don't test 1: it's not useful.
        if num % i == 0:
            factors.append(i)
            otherFactor = int(num / i)
            if otherFactor < MAX_KEY_LENGTH + 1 and otherFactor != 1:
                factors.append(otherFactor)
    return list(set(factors)) # Remove duplicate factors.


def getItemAtIndexOne(x):
    return x[1]


def getMostCommonFactors(seqFactors):
    # First, get a count of how many times a factor occurs in seqFactors:
    factorCounts = {} # Key is a factor; value is how often it occurs.

    # seqFactors keys are sequences; values are lists of factors of the
    # spacings. seqFactors has a value like {'GFD': [2, 3, 4, 6, 9, 12,
    # 18, 23, 36, 46, 69, 92, 138, 207], 'ALW': [2, 3, 4, 6, ...], ...}.
    for seq in seqFactors:
        factorList = seqFactors[seq]
        for factor in factorList:
            if factor not in factorCounts:
                factorCounts[factor] = 0
            factorCounts[factor] += 1

    # Second, put the factor and its count into a tuple and make a list
    # of these tuples so we can sort them:
    factorsByCount = []
    for factor in factorCounts:
        # Exclude factors larger than MAX_KEY_LENGTH:
        if factor <= MAX_KEY_LENGTH:
            # factorsByCount is a list of tuples: (factor, factorCount).
            # factorsByCount has a value like [(3, 497), (2, 487), ...].
            factorsByCount.append( (factor, factorCounts[factor]) )

    # Sort the list by the factor count:
    factorsByCount.sort(key=getItemAtIndexOne, reverse=True)

    return factorsByCount


def kasiskiExamination(ciphertext):
    # Find out the sequences of 3 to 5 letters that occur multiple times
    # in the ciphertext. repeatedSeqSpacings has a value like
    # {'EXG': [192], 'NAF': [339, 972, 633], ... }:
    repeatedSeqSpacings = findRepeatSequencesSpacings(ciphertext)

    # (See getMostCommonFactors() for a description of seqFactors.)
    seqFactors = {}
    for seq in repeatedSeqSpacings:
        seqFactors[seq] = []
        for spacing in repeatedSeqSpacings[seq]:
            seqFactors[seq].extend(getUsefulFactors(spacing))

    # (See getMostCommonFactors() for a description of factorsByCount.)
    factorsByCount = getMostCommonFactors(seqFactors)

    # Now we extract the factor counts from factorsByCount and
    # put them in allLikelyKeyLengths so that they are easier to
    # use later:
    allLikelyKeyLengths = []
    for twoIntTuple in factorsByCount:
        allLikelyKeyLengths.append(twoIntTuple[0])

    return allLikelyKeyLengths


def getNthSubkeysLetters(nth, keyLength, message):
    # Returns every nth letter for each keyLength set of letters in text.
    # E.g. getNthSubkeysLetters(1, 3, 'ABCABCABC') returns 'AAA'
    #      getNthSubkeysLetters(2, 3, 'ABCABCABC') returns 'BBB'
    #      getNthSubkeysLetters(3, 3, 'ABCABCABC') returns 'CCC'
    #      getNthSubkeysLetters(1, 5, 'ABCDEFGHI') returns 'AF'

    # Use a regular expression to remove non-letters from the message:
    message = NONLETTERS_PATTERN.sub('', message.upper())

    i = nth - 1
    letters = []
    while i < len(message):
        letters.append(message[i])
        i += keyLength
    return ''.join(letters)


def attemptHackWithKeyLength(ciphertext, mostLikelyKeyLength):
    # Determine the most likely letters for each letter in the key:
    ciphertextUp = ciphertext.upper()
    # allFreqScores is a list of mostLikelyKeyLength number of lists.
    # These inner lists are the freqScores lists:
    allFreqScores = []
    for nth in range(1, mostLikelyKeyLength + 1):
        nthLetters = getNthSubkeysLetters(nth, mostLikelyKeyLength,
               ciphertextUp)

        # freqScores is a list of tuples like
        # [(, ), ... ]
        # List is sorted by match score. Higher score means better match.
        # See the englishFreqMatchScore() comments in freqAnalysis.py.
        freqScores = []
        for possibleKey in LETTERS:
            decryptedText = vigenereCipher.decryptMessage(possibleKey,
                   nthLetters)
            keyAndFreqMatchTuple = (possibleKey,
                   freqAnalysis.englishFreqMatchScore(decryptedText))
            freqScores.append(keyAndFreqMatchTuple)
        # Sort by match score:
        freqScores.sort(key=getItemAtIndexOne, reverse=True)

        allFreqScores.append(freqScores[:NUM_MOST_FREQ_LETTERS])

    if not SILENT_MODE:
        for i in range(len(allFreqScores)):
            # Use i + 1 so the first letter is not called the "0th" letter:
            print('Possible letters for letter %s of the key: ' % (i + 1),
                   end='')
            for freqScore in allFreqScores[i]:
                print('%s ' % freqScore[0], end='')
            print() # Print a newline.

    # Try every combination of the most likely letters for each position
    # in the key:
    for indexes in itertools.product(range(NUM_MOST_FREQ_LETTERS),
           repeat=mostLikelyKeyLength):
        # Create a possible key from the letters in allFreqScores:
        possibleKey = ''
        for i in range(mostLikelyKeyLength):
            possibleKey += allFreqScores[i][indexes[i]][0]

        if not SILENT_MODE:
            print('Attempting with key: %s' % (possibleKey))

        decryptedText = vigenereCipher.decryptMessage(possibleKey,
               ciphertextUp)

        if detectEnglish.isEnglish(decryptedText):
            # Set the hacked ciphertext to the original casing:
            origCase = []
            for i in range(len(ciphertext)):
                if ciphertext[i].isupper():
                    origCase.append(decryptedText[i].upper())
                else:
                    origCase.append(decryptedText[i].lower())
            decryptedText = ''.join(origCase)

            # Check with user to see if the key has been found:
            print('Possible encryption hack with key %s:' % (possibleKey))
            print(decryptedText[:200]) # Only show first 200 characters.
            print()
            print('Enter D if done, anything else to continue hacking:')
            response = input('> ')

            if response.strip().upper().startswith('D'):
                return decryptedText

    # No English-looking decryption found, so return None:
    return None


def hackVigenere(ciphertext):
    # First, we need to do Kasiski examination to figure out what the
    # length of the ciphertext's encryption key is:
    allLikelyKeyLengths = kasiskiExamination(ciphertext)
    if not SILENT_MODE:
        keyLengthStr = ''
        for keyLength in allLikelyKeyLengths:
            keyLengthStr += '%s ' % (keyLength)
        print('Kasiski examination results say the most likely key lengths
               are: ' + keyLengthStr + '\n')
    hackedMessage = None
    for keyLength in allLikelyKeyLengths:
        if not SILENT_MODE:
            print('Attempting hack with key length %s (%s possible keys)...'
                   % (keyLength, NUM_MOST_FREQ_LETTERS ** keyLength))
        hackedMessage = attemptHackWithKeyLength(ciphertext, keyLength)
        if hackedMessage != None:
            break

    # If none of the key lengths found using Kasiski examination
    # worked, start brute-forcing through key lengths:
    if hackedMessage == None:
        if not SILENT_MODE:
            print('Unable to hack message with likely key length(s). Brute-
                   forcing key length...')
        for keyLength in range(1, MAX_KEY_LENGTH + 1):
            # Don't recheck key lengths already tried from Kasiski:
            if keyLength not in allLikelyKeyLengths:
                if not SILENT_MODE:
                    print('Attempting hack with key length %s (%s possible
                           keys)...' % (keyLength, NUM_MOST_FREQ_LETTERS **
                           keyLength))
                hackedMessage = attemptHackWithKeyLength(ciphertext,
                       keyLength)
                if hackedMessage != None:
                    break
    return hackedMessage


# If vigenereHacker.py is run (instead of imported as a module), call
# the main() function:
if __name__ == '__main__':
    main()

维吉尼亚破解程序的运行示例

当您运行vigenereHacker.py程序时，输出应该如下所示:

Kasiski examination results say the most likely key lengths are: 3 2 6 4 12
Attempting hack with key length 3 (27 possible keys)...
Possible letters for letter 1 of the key: A L M
Possible letters for letter 2 of the key: S N O
Possible letters for letter 3 of the key: V I Z
Attempting with key: ASV
Attempting with key: ASI
--snip--
Attempting with key: MOI
Attempting with key: MOZ
Attempting hack with key length 2 (9 possible keys)...
Possible letters for letter 1 of the key: O A E
Possible letters for letter 2 of the key: M S I
Attempting with key: OM
Attempting with key: OS
--snip--
Attempting with key: ES
Attempting with key: EI
Attempting hack with key length 6 (729 possible keys)...
Possible letters for letter 1 of the key: A E O
Possible letters for letter 2 of the key: S D G
Possible letters for letter 3 of the key: I V X
Possible letters for letter 4 of the key: M Z Q
Possible letters for letter 5 of the key: O B Z
Possible letters for letter 6 of the key: V I K
Attempting with key: ASIMOV
Possible encryption hack with key ASIMOV:
ALAN MATHISON TURING WAS A BRITISH MATHEMATICIAN, LOGICIAN, CRYPTANALYST, AND
COMPUTER SCIENTIST. HE WAS HIGHLY INFLUENTIAL IN THE DEVELOPMENT OF COMPUTER
SCIENCE, PROVIDING A FORMALISATION OF THE CON
Enter D for done, or just press Enter to continue hacking:
> d
Copying hacked message to clipboard:
Alan Mathison Turing was a British mathematician, logician, cryptanalyst, and
computer scientist. He was highly influential in the development of computer
--snip--

导入模块并设置main()函数

让我们看看维吉尼亚破解程序的源代码。破解程序导入了许多不同的模块，包括一个名为itertools的新模块，您将很快了解到更多信息:

# Vigenere Cipher Hacker
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)

import itertools, re
import vigenereCipher, pyperclip, freqAnalysis, detectEnglish

此外，程序在第 7 行到第 11 行设置了几个常量，稍后当它们在程序中使用时我会解释。

破解程序的main()函数类似于之前破解程序中的main()函数:

def main():
    # Instead of typing this ciphertext out, you can copy & paste it
    # from https://www.nostarch.com/crackingcodes/:
    ciphertext = """Adiz Avtzqeci Tmzubb wsa m Pmilqev halpqavtakuoi,
           lgouqdaf, kdmktsvmztsl, izr xoexghzr kkusitaaf. Vz wsa twbhdg
           ubalmmzhdad qz
           --snip--
           azmtmd'g widt ion bwnafz tzm Tcpsw wr Zjrva ivdcz eaigd yzmbo
           Tmzubb a kbmhptgzk dvrvwz wa efiohzd."""
    hackedMessage = hackVigenere(ciphertext)

    if hackedMessage != None:
        print('Copying hacked message to clipboard:')
        print(hackedMessage)
        pyperclip.copy(hackedMessage)
    else:
        print('Failed to hack encryption.')

密文被传递给hackVigenere()函数，如果破解成功，该函数返回解密后的字符串，如果破解失败，则返回None值。如果成功，该程序将被破解的消息打印到屏幕上，并复制到剪贴板上。

寻找重复序列

findRepeatSequencesSpacings()函数通过定位message字符串中所有重复的字母序列并计算序列之间的间距来完成卡西斯基检查的第一步:

def findRepeatSequencesSpacings(message):
         --snip--
    # Use a regular expression to remove non-letters from the message:
    message = NONLETTERS_PATTERN.sub('', message.upper())

    # Compile a list of seqLen-letter sequences found in the message:
    seqSpacings = {} # Keys are sequences; values are lists of int spacings.

第 34 行将消息转换成大写，并使用sub()正则表达式方法从message中删除任何非字母字符。

第 37 行的seqSpacings字典保存重复的序列字符串作为它的密钥，并保存一个列表，其中的整数表示该序列的所有出现之间的字母数作为它的值。例如，如果我们将'PPQCAXQV...'示例字符串作为message传递，findRepeatSequenceSpacings()函数将返回{'VRA': [8, 24, 32], 'AZU': [48], 'YBN': [8]}。

第 38 行的for循环通过查找message中的序列并计算重复序列之间的间隔来检查每个序列是否重复:

    for seqLen in range(3, 6):
        for seqStart in range(len(message) - seqLen):
            # Determine what the sequence is and store it in seq:
            seq = message[seqStart:seqStart + seqLen]

图 20-2：来自消息的序列的值取决于seqStart中的值

在循环的第一次迭代中，代码找到正好三个字母长的序列。在下一次迭代中，它找到正好四个字母长的序列，然后是五个字母长的序列。您可以通过修改第 38 行的range(3, 6)调用来改变代码搜索的序列长度；然而，寻找长度为 3、4 和 5 的重复序列似乎对大多数密文都有效。原因是它们足够长，使得密文中的重复不太可能是巧合，但又足够短，使得重复很可能被发现。for循环当前检查的序列长度存储在seqLen中。

第 39 行的for循环将message分割成每个可能的长度为seqLen的子串。我们将使用这个for循环来确定切片的开始，并将message切片成一个长度为seqLen个字符的子串。例如，如果seqLen是3并且消息是'PPQCAXQ'，我们将希望从第一个索引开始，也就是0，并且切分三个字符以获得子串'PPQ'。然后，我们将转到下一个索引，即1，并切分三个字符以获得子串'PQC'。我们需要对每个索引都这样做，直到最后三个字符，这是相当于len(message) – seqLen的索引。这样做，你将得到如图 20-2 所示的序列。

第 39 行的for循环遍历到len(message) – seqLen的每个索引，并将当前索引分配给变量seqStart作为子串片的开始。有了起始索引后，第 41 行将seq变量设置为子字符串片。

我们将使用第 44 行的for循环在消息中搜索该片段的重复。

            # Look for this sequence in the rest of the message:
            for i in range(seqStart + seqLen, len(message) - seqLen):
                if message[i:i + seqLen] == seq:

第 44 行的for循环位于第 39 行的for循环内，并将i设置为message中长度为seqLen的每个可能序列的索引。这些索引从seqStart + seqLen开始，或者在当前seq中的序列之后，一直到len(message) - seqLen，这是可以找到长度为seqLen的序列的最后一个索引。例如，如果message是'PPQCAXQVEKGYBNKMAZUYBN'，seqStart是11，seqLen是3，第 41 行将seq设置为'YBN'。for循环将从索引14开始查看message。

第 45 行的表达式message[i:i + seqLen]计算出message的子串，与seq进行比较，检查子串是否是seq的重复。如果是，第 46 到 52 行计算间距并将其添加到seqSpacings字典中。在第一次迭代中，第 45 行比较'KMA'和seq，然后在下一次迭代中比较'MAZ'和seq，然后在下一次迭代中比较'AZU'和seq，依此类推。当i为19时，第 45 行发现'YBN'等于seq，执行运行第 46 至 52 行:

                    # Found a repeated sequence:
                    if seq not in seqSpacings:
                        seqSpacings[seq] = [] # Initialize blank list.

                    # Append the spacing distance between the repeated
                    # sequence and the original sequence:
                    seqSpacings[seq].append(i - seqStart)

第 47 和 48 行检查seq变量是否作为键存在于seqSpacings中。如果没有，seqSpacings[seq]被设置为一个键，其值为一个空白列表。

在message[i:i + seqLen]的序列和在message[seqStart:seqStart+seqLen]的原始序列之间的字母数就是i - seqStart。注意i和seqStart是冒号前的开始索引。因此，i - seqStart计算的整数是两个序列之间的字母数，我们将其添加到存储在seqSpacings[seq]的列表中。

当所有这些for循环完成后，seqSpacings字典应该包含长度为 3、4 和 5 的每个重复序列，以及重复序列之间的字母数。seqSpacings字典从第 53 行的findRepeatSequencesSpacings()返回:

    return seqSpacings

现在，您已经看到了程序如何通过查找密文中的重复序列并计算它们之间的字母数量来执行卡西斯基检查的第一步，让我们看看程序如何进行卡西斯基检查的下一步。

计算间隔系数

回想一下，卡西斯基检查的下一步包括寻找间距的因数。我们正在寻找长度在2和MAX_KEY_LENGTH之间的因数。为此，我们将创建getUsefulFactors()函数，该函数采用一个num参数并返回一个只包含符合该标准的因数的列表。

def getUsefulFactors(num):
         --snip--
    if num < 2:
        return [] # Numbers less than 2 have no useful factors.

    factors = [] # The list of factors found.

第 61 行检查num小于2的特殊情况。在这种情况下，第 62 行返回空列表，因为如果num小于2，它将没有任何有用的因数。

如果num大于2，我们需要计算num的所有因数，并将它们存储在一个列表中。在第 64 行，我们创建一个名为factors的空列表来存储因数。

第 68 行的for循环遍历从2到MAX_KEY_LENGTH的整数，包括MAX_KEY_LENGTH中的值。记住，因为range()导致for循环迭代到但不包括第二个参数，所以我们传递MAX_KEY_LENGTH + 1以便包含MAX_KEY_LENGTH。这个循环找到了num的所有因数。

    for i in range(2, MAX_KEY_LENGTH + 1): # Don't test 1: it's not useful.
        if num % i == 0:
            factors.append(i)
            otherFactor = int(num / i)

第 69 行测试num % i是否等于0；如果是，我们知道i将num平均分，没有余数，也就是说i是num的一个因数。在这种情况下，第 70 行将i添加到factors变量的因数列表中。因为我们知道num / i也必须平分num，所以第 71 行将它的整数形式存储在otherFactor中。（记住/操作符总是计算浮点值，比如21 / 7计算浮点值3.0而不是整数3。）如果结果值是1，程序不将它包含在factors列表中，所以第 72 行检查这种情况:

            if otherFactor < MAX_KEY_LENGTH + 1 and otherFactor != 1:
                factors.append(otherFactor)

如果它不是1，第 73 行追加该值。我们排除了1,因为如果维吉尼亚密钥的长度为 1，那么维吉尼亚密码将与凯撒密码没有什么不同！

用set()函数删除重复

回想一下，作为卡西斯基检查的一部分，我们需要知道最常见的因数，因为最常见的因数几乎肯定是维吉尼亚密钥的长度。然而，在我们分析每个因数的频率之前，我们需要使用set()函数从factors列表中删除任何重复的因数。例如，如果getUsefulFactors()被传递给num参数的9，那么9 % 3 == 0将是True，并且i和otherFactor都将被附加到factors。但是i和int(num / i)都等于3，所以3会被追加到列表中两次。为了防止重复的数字，我们可以将列表传递给set()，它返回一个列表作为设置的数据类型。集合数据类型类似于列表数据类型，除了集合值只能包含唯一值。

您可以将任何列表值传递给set()函数，以获得一个没有任何重复值的集合值。相反，如果您将一个集合值传递给list()，它将返回该集合的列表值版本。要查看这方面的示例，请在交互式 shell 中输入以下内容:

>>> set([1, 2, 3, 3, 4])
set([1, 2, 3, 4])
>>> spam = list(set([2, 2, 2, 'cats', 2, 2]))
>>> spam
[2, 'cats']

当列表转换为集合时，任何重复的列表值都将被删除。即使将从列表转换的集合重新转换为列表，它也不会有任何重复的值。

去除重复因数并排序列表

第 74 行将factors中的列表值传递给set()以删除任何重复的因数:

    return list(set(factors)) # Remove duplicate factors.

第 77 行的函数getItemAtIndexOne()几乎与你在第 19 章中编写的freqAnalysis.py程序中的getItemAtIndexZero（参见第 268 页上的获取元组的第一个成员）:

def getItemAtIndexOne(x):
    return x[1]

该函数将在程序的后面被传递给sort()以基于被排序的项目的索引1处的项目进行排序。

寻找最常见的因数

为了找到最常见的因数，也就是最可能的密钥长度，我们需要编写getMostCommonFactors()函数，从第 81 行开始。

def getMostCommonFactors(seqFactors):
   # First, get a count of how many times a factor occurs in seqFactors:
   factorCounts = {} # Key is a factor; value is how often it occurs.

第 81 行的seqFactors参数接受一个使用kasiskiExamination()函数创建的字典值，我将很快对此进行解释。该字典将序列字符串作为键，将整数因数列表作为每个键的值。（这些是findRepeatSequencesSpacings ()之前返回的间隔整数的因数。）例如，seqFactors可能包含如下所示的字典值:

{'VRA': [8, 2, 4, 2, 3, 4, 6, 8, 12, 16, 8, 2, 4], 'AZU': [2, 3, 4, 6, 8, 12,
 16, 24], 'YBN': [8, 2, 4]}

getMostCommonFactors()函数对seqFactors中最常见的因数进行排序，从最频繁出现的到最不频繁出现的，并将它们作为双整数元组列表返回。元组中的第一个整数是因数，第二个整数是它在seqFactors中出现了多少次。

例如，getMostCommonFactors()可能返回一个列表值，如下所示:

[(3, 556), (2, 541), (6, 529), (4, 331), (12, 325), (8, 171), (9, 156), (16,
105), (5, 98), (11, 86), (10, 84), (15, 84), (7, 83), (14, 68), (13, 52)]

这个列表显示，在传递给getMostCommonFactors ()的seqFactors字典中，因数 3 出现了 556 次，因数 2 出现了 541 次，因数 6 出现了 529 次，以此类推。注意，3 出现在列表的第一位，因为它是最常见的因数；13 是最不常见的因数，因此在列表中排在最后。

对于getMostCommonFactors()的第一步，我们将在第 83 行设置factorCounts字典，我们将使用它来存储每个因数的计数。factorCounts的键将是因数，与键相关联的值将是那些因数的计数。

接下来，第 88 行的for循环遍历seqFactors中的每个序列，在每次迭代中将其存储在一个名为seq的变量中。用于seq的seqFactors中的因数列表存储在第 89 行名为factorList的变量中:

    for seq in seqFactors:
        factorList = seqFactors[seq]
        for factor in factorList:
            if factor not in factorCounts:
                factorCounts[factor] = 0
            factorCounts[factor] += 1

该列表中的因数在第 90 行用for循环。如果一个因数在factorCounts中不作为关键字存在，它会在第 92 行添加一个值0。第 93 行增加了factorCounts[factor]，这是factorCounts中因数的值。

对于getMostCommonFactors()的第二步，我们需要按照计数对factorCounts字典中的值进行排序。但是因为字典值没有排序，我们必须首先将字典转换成两个整数元组的列表。（我们在freqanalysis.py模块的getFrequencyOrder()函数中的第 19 章做了类似的事情。）我们将这个列表值存储在一个名为factorsByCount的变量中，这个变量从第 97 行的空列表开始:

    factorsByCount = []
    for factor in factorCounts:
        # Exclude factors larger than MAX_KEY_LENGTH:
        if factor <= MAX_KEY_LENGTH:
            # factorsByCount is a list of tuples: (factor, factorCount).
            # factorsByCount has a value like [(3, 497), (2, 487), ...].
            factorsByCount.append( (factor, factorCounts[factor]) )

然后，第 98 行的for循环遍历factorCounts中的每个因数，只有当因数小于或等于MAX_KEY_LENGTH时，才将这个(factor, factorCounts[factor])元组追加到factorsByCount列表中。

在for循环完成将所有元组添加到factorsByCount之后，第 106 行将factorsByCount排序为getMostCommonFactors()函数的最后一步。

    factorsByCount.sort(key=getItemAtIndexOne, reverse=True)

    return factorsByCount

因为getItemAtIndexOne函数是为key关键字参数传递的，而True是为reverse关键字参数传递的，所以列表按因数计数降序排序。第 108 行返回factorsByCount中的排序列表，它应该指出哪些因数出现得最频繁，因此最有可能是维吉尼亚密钥长度。

寻找最可能的密钥长度

在我们弄清楚密文可能的子密钥是什么之前，我们需要知道有多少个子密钥。也就是我们需要知道密钥的长度。第 111 行的kasiskiExamination()函数返回给定ciphertext参数的最可能的密钥长度列表。

def kasiskiExamination(ciphertext):
         --snip--
    repeatedSeqSpacings = findRepeatSequencesSpacings(ciphertext)

密钥长度是列表中的整数；列表中的第一个整数是最可能的密钥长度，第二个整数是第二可能的长度，依此类推。

寻找密钥长度的第一步是找到密文中重复序列之间的间隔。这是从函数findRepeatSequencesSpacings()返回的，作为一个字典，序列字符串作为它的键，一个列表，间隔作为整数作为它的值。第 294 页的寻找重复序列中已经描述了findRepeatSequencesSpacings函数。

在继续下一行代码之前，您需要了解一下extend()列表方法。

append()列表方法

当你需要在列表末尾添加多个值时，有一种比在循环中调用append()更简单的方法。与append()列表方法类似，extend()列表方法可以将值添加到列表的末尾。当传递一个列表时，append()方法将整个列表作为一个条目添加到另一个列表的末尾，如下所示:

>>> spam = ['cat', 'dog', 'mouse']
>>> eggs = [1, 2, 3]
>>> spam.append(eggs)
>>> spam
['cat', 'dog', 'mouse', [1, 2, 3]]

相反，extend()方法将列表参数中的每一项添加到列表的末尾。在交互式 shell 中输入以下内容以查看示例:

>>> spam = ['cat', 'dog', 'mouse']
>>> eggs = [1, 2, 3]
>>> spam.extend(eggs)
>>> spam
['cat', 'dog', 'mouse', 1, 2, 3]

如您所见，eggs ( 1、2和3）中的所有值都作为离散项追加到spam中。

扩展repeatedSeqSpacings字典

虽然repeatedSeqSpacings是一个将序列字符串映射到整数间隔列表的字典，但我们实际上需要一个将序列字符串映射到那些整数间隔的因数列表的字典。（原因请参见第 283 页的上的获取间距系数。）第 118 到 122 行是这样做的:

    seqFactors = {}
    for seq in repeatedSeqSpacings:
        seqFactors[seq] = []
        for spacing in repeatedSeqSpacings[seq]:
            seqFactors[seq].extend(getUsefulFactors(spacing))

第 118 行从seqFactors中的一个空字典开始。第 119 行的for循环遍历字典repeatedSeqSpacings中的每个键，这是一个序列字符串。对于每个键，第 120 行将一个空白列表设置为seqFactors中的值。

第 121 行的for循环通过将每个间隔整数传递给一个getUsefulFactors()调用来迭代所有的间隔整数。使用extend()方法将从getUsefulFactors()返回的列表中的每个项目添加到seqFactors[seq]。当所有的for循环完成后，seqFactors应该是一个将序列字符串映射到整数间隔的因数列表的字典。这允许我们有间距的因数，而不仅仅是间距。

第 125 行将seqFactors字典传递给getMostCommonFactors()函数，并返回一个双整数元组列表，其第一个整数代表因数，第二个整数显示该因数在seqFactors中出现的频率。然后元组被存储在factorsByCount中。

    factorsByCount = getMostCommonFactors(seqFactors)

但是我们希望kasiskiExamination()函数返回整数因数的列表，而不是包含因数和因数出现频率的元组列表。因为这些因数在factorsByCount中存储为双整数元组列表的第一项，所以我们需要从元组中提取这些因数，并将它们放在一个单独的列表中。

从factorsByCount中获取因数

第 130 到 134 行在allLikelyKeyLengths中存储了单独的因数列表。

    allLikelyKeyLengths = []
    for twoIntTuple in factorsByCount:
        allLikelyKeyLengths.append(twoIntTuple[0])

    return allLikelyKeyLengths

第 131 行的for循环遍历factorsByCount中的每个元组，并将元组的索引0项附加到allLikelyKeyLengths的末尾。在这个for循环完成后，allLikelyKeyLengths变量应该包含factorsByCount中的所有整数因数，这些因数作为一个列表从kasiskiExamination()返回。

尽管我们现在有能力找到消息加密时可能使用的密钥长度，但我们需要能够从消息中分离出使用相同子密钥加密的字母。回想一下，用密钥'XYZ'加密'THEDOGANDTHECAT'最终会使用密钥中的'X'来加密索引0、3、6、9和12处的消息字母。因为来自原始英文消息的这些字母是用相同的子密钥（'X'）加密的，所以解密的文本应该具有类似于英文的字母频率计数。我们可以使用这些信息来找出子密钥。

获取用相同子密钥加密的字母

为了从用相同的子密钥加密的密文中提取出字母，我们需要编写一个函数，使用消息的第一、第二或第n个字母创建一个字符串。在函数有了起始索引、密钥长度和传递给它的消息之后，第一步是使用第 145 行的正则表达式对象及其sub()方法从message中删除非字母字符。

注

正则表达式在第 230 页的“使用正则表达式查找字符”中讨论。

这个只有字母的字符串然后作为新值存储在message中:

def getNthSubkeysLetters(nth, keyLength, message):
         --snip--
    message = NONLETTERS_PATTERN.sub('', message.upper())

接下来，我们通过将字母字符串附加到一个列表来构建一个字符串，然后使用join()将列表合并成一个字符串:

    i = nth - 1
    letters = []
    while i < len(message):
        letters.append(message[i])
        i += keyLength
    return ''.join(letters)

i变量指向message中要添加到字符串构建列表中的字母的索引，该列表存储在名为letters的变量中。i变量从第 147 行的值nth - 1开始，letters变量从第 148 行的空白列表开始。

只要i小于message的长度，第 149 行的while循环就会继续运行。在每次迭代中，message[i]处的字母被添加到letters中的列表中。然后通过将第 151 行上的keyLength加到i来更新i以指向子密钥中的下一个字母。

这个循环结束后，第 152 行将letters列表中的单字母字符串值连接成一个字符串，这个字符串从getNthSubkeysLetters()返回。

现在我们可以取出用相同的子密钥加密的字母，我们可以使用getNthSubkeysLetters()尝试用一些潜在的密钥长度解密。

尝试用可能的密钥长度解密

回想一下,kasiskiExamination()函数并不保证返回维吉尼亚密钥的实际长度，而是返回几个可能长度的列表，按照最可能的密钥长度到最不可能的密钥长度排序。如果代码确定了错误的密钥长度，它将使用不同的密钥长度重试。当传递了密文和确定的密钥长度时,attemptHackWithKeyLength()函数会这样做。如果成功，该函数将返回被攻击消息的字符串。如果破解失败，函数返回None。

黑客代码只对大写字母起作用，但是我们想要返回任何解密的字符串和它原来的大小写，所以我们需要保留原来的字符串。为此，我们将大写形式的ciphertext字符串存储在第 157 行名为ciphertextUp的单独变量中。

def attemptHackWithKeyLength(ciphertext, mostLikelyKeyLength):
    # Determine the most likely letters for each letter in the key:
    ciphertextUp = ciphertext.upper()

如果我们假设mostLikelyKeyLength中的值是正确的密钥长度，黑客算法为每个子密钥调用getNthSubkeysLetters(),然后在 26 个可能的字母中寻找产生解密文本的字母，其字母频率与该子密钥的英语字母频率最接近。

首先，在第 160 行的allFreqScores中存储一个空列表，它将存储由freqAnalysis.englishFreqMatchScore()返回的频率匹配分数:

    allFreqScores = []
    for nth in range(1, mostLikelyKeyLength + 1):
        nthLetters = getNthSubkeysLetters(nth, mostLikelyKeyLength,
               ciphertextUp)

第 161 行的for循环将nth变量设置为从1到mostLikelyKeyLength值的每个整数。回想一下，当range()被传递了两个参数时，范围上升到第二个参数，但不包括第二个参数。将+ 1放入代码中，使mostLikelyKeyLength中的整数值包含在返回的范围对象中。

第n个子项的字母从第 162 行的getNthSubkeysLetters()返回。

接下来，我们需要用所有 26 个可能的子密钥来解密第n个子密钥的字母，看看哪一个产生了类似英语的字母频率。英语频率匹配分数列表存储在名为freqScores的变量列表中。这个变量从第 168 行的空列表开始，然后第 169 行的for循环遍历LETTERS字符串中的 26 个大写字母:

        freqScores = []
        for possibleKey in LETTERS:
            decryptedText = vigenereCipher.decryptMessage(possibleKey,
                   nthLetters)

possibleKey值通过调用第 170 行的vigenereCipher.decryptMessage()来解密密文。在possibleKey中的子密钥只有一个字母，但是在nthLetters中的字符串只由来自message的字母组成，如果代码已经正确地确定了密钥长度，那么这些字母已经用那个子密钥加密了。

然后，解密后的文本被传递给freqAnalysis.englishFreqMatchScore()，以查看decryptedText中的字母频率与常规英语的字母频率有多接近。正如你在第 19 章中了解到的，返回值是一个介于0和12之间的整数:回想一下，更大的数字意味着更接近的匹配。

第 171 行将这个频率匹配分数和用于解密的密钥放入一个元组，并将其存储在keyAndFreqMatchTuple变量中。这个元组被附加到第 172 行的freqScores的末尾:

            keyAndFreqMatchTuple = (possibleKey,
                   freqAnalysis.englishFreqMatchScore(decryptedText))
            freqScores.append(keyAndFreqMatchTuple)

在第 169 行的for循环完成之后，freqScores列表应该包含 26 个关键字和频率匹配分数元组:26 个子关键字中的每一个都有一个元组。我们需要对这个列表进行排序，使具有最大英语频率匹配分数的元组排在最前面。这意味着我们希望按照索引1的值对freqScores中的元组进行反向（降序）排序。

我们在freqScores列表上调用sort()方法，为key关键字参数传递函数值getItemAtIndexOne。注意，我们不是在调用函数，这可以从缺少括号中看出。值True被传递给reverse关键字参数，以便按降序排序。

        freqScores.sort(key=getItemAtIndexOne, reverse=True)

最初，NUM_MOST_FREQ_LETTERS常量被设置为第 9 行的整数值4。在以逆序对freqScores中的元组排序之后，第 176 行将仅包含前三个元组或者具有三个最高英语频率匹配分数的元组的列表附加到allFreqScores。因此，allFreqScores[0]包含第一个子密钥的频率分数，allFreqScores[1]包含第二子密钥的频率分数，依此类推。

        allFreqScores.append(freqScores[:NUM_MOST_FREQ_LETTERS])

在第 161 行的for循环完成后，allFreqScores应该包含与mostLikelyKeyLength中的整数值相等的多个列表值。例如，如果mostLikelyKeyLength是3，allFreqScores将是三个列表的列表。第一个列表值保存完整维吉尼亚密钥的第一个子密钥的前三个最高匹配子密钥的元组。第二个列表值保存完整维吉尼亚密钥的第二个子密钥的前三个最高匹配子密钥的元组，依此类推。

最初，如果我们想要暴力破解整个维吉尼亚密钥，可能的密钥数量将是 26 的密钥长度次方。例如，如果密钥是长度为 7 的 ROSEBUD，则可能有26 ** 7，即 8，031，810，176 个密钥。

但是检查英语频率匹配有助于确定每个子项的四个最可能的字母。继续 ROSEBUD 的例子，这意味着我们只需要检查4 ** 7，或者 16384 个可能的密钥，这比 80 亿个可能的密钥有了巨大的改进！

print()的end关键字参数

接下来，我们希望向用户打印输出。为此，我们使用print()，但是将一个参数传递给一个我们以前没有使用过的可选参数。每当调用print()函数时，它都会将传递给它的字符串和换行符一起打印到屏幕上。要在字符串末尾打印其他内容而不是换行符，我们可以为print()函数的end关键字参数指定字符串。在交互式 shell 中输入以下内容，查看如何使用print()函数的end关键字参数:

   >>> def printStuff():
           print('Hello', end='\n') # ➊
           print('Howdy', end='') # ➋
           print('Greetings', end='XYZ') # ➌
           print('Goodbye')
   >>> printStuff()
   Hello
   HowdyGreetingsXYZGoodbye

通过end='\n'正常打印字符串 ➊。但是，传递end='' ➋ 或end='XYZ' ➌ 会替换通常的换行符，因此后续的print()调用不会显示在新的一行上。

以静默模式运行程序或向用户打印信息

此时，我们想知道哪个字母是每个子项的前三个候选字母。如果SILENT_MODE常量在程序的早期被设置为False，第 178 到 184 行的代码会将allFreqScores中的值打印到屏幕上:

    if not SILENT_MODE:
        for i in range(len(allFreqScores)):
            # Use i + 1 so the first letter is not called the "0th" letter:
            print('Possible letters for letter %s of the key: ' % (i + 1),
                   end='')
            for freqScore in allFreqScores[i]:
                print('%s ' % freqScore[0], end='')
            print() # Print a newline.

如果SILENT_MODE被设置为True，那么if语句块中的代码将被跳过。

我们现在已经将子项的数量减少到一个足够小的数量，我们可以暴力破解所有子项。接下来，您将学习如何使用itertools .product()函数来生成所有可能的子机码组合以进行暴力破解。

寻找子项的可能组合

现在我们有了可能的子项，我们需要将它们放在一起以找到整个项。问题是，即使我们已经为每个子项找到了字母，最有可能的字母实际上可能不是正确的字母。相反，第二个或第三个最有可能的字母可能是正确的子密钥字母。这意味着我们不能将每个子项最可能的字母组合成一个密钥:我们需要尝试不同的可能字母组合来找到正确的密钥。

vigenereHacker.py程序使用itertools.product()函数来测试所有可能的子密钥组合。

itertools.product()函数

itertools.product()函数产生列表或类似列表的值中所有可能的项目组合，比如字符串或元组。这样的项目组合被称为笛卡尔积，这也是该函数得名的原因。该函数返回一个itertools结果对象值，该值也可以通过传递给list()转换成一个列表。在交互式 shell 中输入以下内容以查看示例:

   >>> import itertools
   >>> itertools.product('ABC', repeat=4)
   <itertools.product object at 0x02C40170> # ➊
   >>> list(itertools.product('ABC', repeat=4))
   [('A', 'A', 'A', 'A'), ('A', 'A', 'A', 'B'), ('A', 'A', 'A', 'C'), ('A', 'A',
   'B', 'A'), ('A', 'A', 'B', 'B'), ('A', 'A', 'B', 'C'), ('A', 'A', 'C', 'A'),
   ('A', 'A', 'C', 'B'), ('A', 'A', 'C', 'C'), ('A', 'B', 'A', 'A'), ('A', 'B',
   'A', 'B'), ('A', 'B', 'A', 'C'), ('A', 'B', 'B', 'A'), ('A', 'B', 'B', 'B'),
   --snip--
   ('C', 'B', 'C', 'B'), ('C', 'B', 'C', 'C'), ('C', 'C', 'A', 'A'), ('C', 'C',
   'A', 'B'), ('C', 'C', 'A', 'C'), ('C', 'C', 'B', 'A'), ('C', 'C', 'B', 'B'),
   ('C', 'C', 'B', 'C'), ('C', 'C', 'C', 'A'), ('C', 'C', 'C', 'B'), ('C', 'C',
   'C', 'C')]

将'ABC'和repeat关键字参数的整数4传递给itertools .product()会返回一个itertools结果对象 ➊，当转换为一个列表时，该对象包含四个值的元组，每个值都有'A'、'B'和'C'的可能组合。这产生了一个总共有3 ** 4或 81 个元组的列表。

还可以将列表值传递给itertools.product()以及一些类似于列表的值，比如从range()返回的范围对象。在交互式 shell 中输入以下内容，看看当列表和类似列表的对象被传递给这个函数时会发生什么:

>>> import itertools
>>> list(itertools.product(range(8), repeat=5))
[(0, 0, 0, 0, 0), (0, 0, 0, 0, 1), (0, 0, 0, 0, 2), (0, 0, 0, 0, 3), (0, 0, 0,
0, 4), (0, 0, 0, 0, 5), (0, 0, 0, 0, 6), (0, 0, 0, 0, 7), (0, 0, 0, 1, 0), (0,
0, 0, 1, 1), (0, 0, 0, 1, 2), (0, 0, 0, 1, 3), (0, 0, 0, 1, 4),
--snip--
(7, 7, 7, 6, 6), (7, 7, 7, 6, 7), (7, 7, 7, 7, 0), (7, 7, 7, 7, 1), (7, 7, 7,
7, 2), (7, 7, 7, 7, 3), (7, 7, 7, 7, 4), (7, 7, 7, 7, 5), (7, 7, 7, 7, 6), (7,
7, 7, 7, 7)]

当从range(8)返回的范围对象和repeat关键字参数的5一起传递给itertools.product()时，它生成一个包含五个值的元组的列表，整数范围从0到7。

我们不能仅仅传递给itertools.product()一个潜在子密钥字母的列表，因为该函数创建相同值的组合，并且每个子密钥可能有不同的潜在字母。相反，因为我们的子密钥存储在allFreqScores的元组中，我们将通过索引值访问这些字母，索引值的范围从 0 到我们想要尝试的字母数减 1。我们知道每个元组中的字母数等于NUM_MOST_FREQ_LETTERS，因为我们只在前面的第 176 行存储了每个元组中的潜在字母数。因此，我们需要访问的索引范围是从0到NUM_MOST_FREQ_LETTERS，这是我们将传递给itertools .product()的内容。我们还将传递itertools.product()一个可能的密钥长度作为第二个参数，创建与潜在密钥长度一样长的元组。

例如，如果我们想只尝试每个子密钥的前三个最可能的字母（由NUM_MOST_FREQ_LETTERS决定）作为一个可能有五个字母长的密钥，itertools.product()产生的第一个值将是(0, 0, 0, 0, 0)。下一个值将是(0, 0, 0, 0, 1)，然后是(0, 0, 0, 0, 2)，并且将生成值，直到到达(2, 2, 2, 2, 2)。五值元组中的每个整数代表一个对allFreqScores的索引。

访问allFreqScores中的子项

allFreqScores中的值是一个列表，它包含每个子项最可能的字母以及它们的频率匹配分数。为了查看这个列表是如何工作的，让我们在空闲时创建一个假设的allFreqScores值。例如，allFreqScores可能是这样一个六个字母的密钥，我们为每个子项找到了四个最可能的字母:

>>> allFreqScores = [[('A', 9), ('E', 5), ('O', 4), ('P', 4)], [('S', 10),
('D', 4), ('G', 4), ('H', 4)], [('I', 11), ('V', 4), ('X', 4), ('B', 3)],
[('M', 10), ('Z', 5), ('Q', 4), ('A', 3)], [('O', 11), ('B', 4), ('Z', 4),
('A', 3)], [('V', 10), ('I', 5), ('K', 5), ('Z', 4)]]

这看起来可能很复杂，但是我们可以通过索引深入到列表和元组的特定值。当在索引处访问allFreqScores时，它求值单个子密钥的可能字母的元组列表以及它们的频率匹配分数。例如，allFreqScores[0]具有第一个子密钥的元组列表以及每个潜在子密钥的频率匹配分数，allFreqScores[1]具有第二个子密钥的元组列表和频率匹配分数，等等:

>>> allFreqScores[0]
[('A', 9), ('E', 5), ('O', 4), ('P', 4)]
>>> allFreqScores[1]
[('S', 10), ('D', 4), ('G', 4), ('H', 4)]

您还可以通过添加额外的索引引用来访问每个子项的每个可能字母元组。例如，如果我们访问allFreqScores[1][0]、来自allFreqScores [1][1]的第二个最可能的字母，等等，我们将得到最可能是第二个子密钥的字母的元组及其频率匹配分数:

>>> allFreqScores[1][0]
('S', 10)
>>> allFreqScores[1][1]
('D', 4)

因为这些值是元组，所以我们需要访问元组中的第一个值，以获得可能的字母，而不包括其频率匹配分值。每个字母都存储在元组的第一个索引中，因此我们将使用allFreqScores[1][0][0]来访问第一个子密钥最可能的字母，allFreqScores [1][1][0]来访问第二子密钥最可能的字母，依此类推:

>>> allFreqScores[1][0][0]
'S'
>>> allFreqScores[1][1][0]
'D'

一旦您能够在allFreqScores中访问潜在的子项，您需要将它们组合起来以找到潜在的项。

使用itertools.product()创建子项组合

由itertools.product()产生的元组每个代表一个密钥，其中元组中的位置对应于我们在allFreqScores中访问的第一个索引，元组中的整数代表我们在allFreqScores中访问的第二个索引。

因为我们之前将NUM_MOST_FREQ_LETTERS常量设置为4，所以第 188 行的itertools.product(range(NUM_MOST_FREQ_LETTERS), repeat=mostLikelyKeyLength)导致for循环有一个整数元组（从0到3，代表indexes变量的每个子项的四个最可能的字母:

    for indexes in itertools.product(range(NUM_MOST_FREQ_LETTERS),
           repeat=mostLikelyKeyLength):
        # Create a possible key from the letters in allFreqScores:
        possibleKey = ''
        for i in range(mostLikelyKeyLength):
            possibleKey += allFreqScores[i][indexes[i]][0]

我们使用indexes构造完整的维吉尼亚密钥，它在每次迭代中接受由itertools.product()创建的一个元组的值。这个密钥从第 190 行的空字符串开始，第 191 行的for循环遍历从0到mostLikelyKeyLength的整数，为每个元组构造一个密钥。

随着for循环的每次迭代中i变量的变化，indexes[i]的值就是我们想要在allFreqScores[i]中使用的元组的索引。这就是为什么allFreqScores[i][indexes[i]]计算出我们想要的正确的元组。当我们拥有正确的元组时，我们需要访问该元组中的索引0来获取子密钥字母。

如果SILENT_MODE是False，第 195 行打印由第 191 行的for循环创建的密钥:

        if not SILENT_MODE:
            print('Attempting with key: %s' % (possibleKey))

现在我们有了一个完整的维吉尼亚密钥，第 197 到 208 行解密密文并检查解密的文本是否是可读的英语。如果是，程序将它打印到屏幕上，让用户确认它确实是英语，以检查误报。

用正确的大小写打印解密文本

因为decryptedText是大写的，所以第 201 到 207 行通过将decryptedText中字母的大写或小写形式追加到origCase列表来构建一个新字符串:

        decryptedText = vigenereCipher.decryptMessage(possibleKey,
               ciphertextUp)

        if detectEnglish.isEnglish(decryptedText):
            # Set the hacked ciphertext to the original casing:
            origCase = []
            for i in range(len(ciphertext)):
                if ciphertext[i].isupper():
                    origCase.append(decryptedText[i].upper())
                else:
                    origCase.append(decryptedText[i].lower())
            decryptedText = ''.join(origCase)

第 202 行上的for循环遍历ciphertext管柱中的每个索引，与ciphertextUp不同，其具有ciphertext的原始套管。如果ciphertext[i]是大写的，则decryptedText[i]的大写形式被附加到origCase上。否则，会附加小写形式的decryptedText[i]。然后将origCase中的列表连接到第 207 行，成为decryptedText的新值。

下面几行代码将解密输出打印给用户，以检查是否找到了密钥:

            print('Possible encryption hack with key %s:' % (possibleKey))
            print(decryptedText[:200]) # Only show first 200 characters.
            print()
            print('Enter D if done, anything else to continue hacking:')
            response = input('> ')

            if response.strip().upper().startswith('D'):
                return decryptedText

大小写正确的解密文本被打印到屏幕上，供用户确认是英语。如果用户输入'D'，函数返回decryptedText字符串。

否则，如果没有一个解密看起来像英语，则破解失败，并且返回None值:

    return None

返回破解消息

最后，我们定义的所有函数都将由hackVigenere ()函数使用，该函数接受一个密文字符串作为参数，并返回被攻击的消息（如果攻击成功）或None（如果没有成功）。首先用kasiskiExamination()获得可能的密钥长度:

def hackVigenere(ciphertext):
    # First, we need to do Kasiski examination to figure out what the
    # length of the ciphertext's encryption key is:
    allLikelyKeyLengths = kasiskiExamination(ciphertext)

hackVignere()函数的输出取决于程序是否在SILENT_MODE中:

    if not SILENT_MODE:
        keyLengthStr = ''
        for keyLength in allLikelyKeyLengths:
            keyLengthStr += '%s ' % (keyLength)
        print('Kasiski examination results say the most likely key lengths
               are: ' + keyLengthStr + '\n')

如果SILENT_MODE为False，则可能的密钥长度被打印到屏幕上。

接下来，我们需要为每个密钥长度找到可能的子密钥字母。我们将使用另一个循环来实现这一点，该循环试图用我们找到的每个密钥长度来破解密码。

找到潜在密钥时跳出循环

我们希望代码继续循环并检查密钥长度，直到找到可能正确的密钥长度。当它发现一个似乎正确的密钥长度时，我们将使用一个break语句来停止循环。

类似于在循环中使用continue语句返回到循环的开始，在循环中使用break语句立即退出循环。当程序执行中断循环时，它会在循环结束后立即移动到第一行代码。每当程序找到一个可能正确的密钥，并需要用户确认该密钥是否正确时，我们就会跳出这个循环。

    hackedMessage = None
    for keyLength in allLikelyKeyLengths:
        if not SILENT_MODE:
            print('Attempting hack with key length %s (%s possible keys)...'
                   % (keyLength, NUM_MOST_FREQ_LETTERS ** keyLength))
        hackedMessage = attemptHackWithKeyLength(ciphertext, keyLength)
        if hackedMessage != None:
            break

对于每个可能的密钥长度，代码在第 236 行调用attemptHackWithKeyLength()。如果attemptHackWithKeyLength()没有返回None，破解就成功了，程序执行应该在第 238 行跳出for循环。

暴力破解其他所有密钥长度

如果黑客没有通过kasiskiExamination()返回的所有可能的密钥长度，当第 242 行的if语句执行时，hackedMessage被设置为None。在这种情况下，所有长度达到MAX_KEY_LENGTH的其他键都会被尝试。如果卡西斯基检查未能计算出正确的密钥长度，我们可以使用第 245 行的for循环暴力破解密钥长度:

    if hackedMessage == None:
        if not SILENT_MODE:
            print('Unable to hack message with likely key length(s). Brute-
                   forcing key length...')
        for keyLength in range(1, MAX_KEY_LENGTH + 1):
            # Don't recheck key lengths already tried from Kasiski:
            if keyLength not in allLikelyKeyLengths:
                if not SILENT_MODE:
                    print('Attempting hack with key length %s (%s possible
                           keys)...' % (keyLength, NUM_MOST_FREQ_LETTERS **
                             keyLength))
                hackedMessage = attemptHackWithKeyLength(ciphertext,
                       keyLength)
                if hackedMessage != None:
                    break

第 245 行开始一个for循环，只要不在allLikelyKeyLengths中，就为keyLength（范围从1到MAX_KEY_LENGTH）的每个值调用attemptHackWithKeyLength()。原因是allLikelyKeyLengths中的密钥长度已经在第 233 到 238 行的代码中试过了。

最后，hackedMessage中的值在第 253 行返回:

    return hackedMessage

调用main()函数

如果这个程序是自己运行的，而不是由另一个程序导入的，那么第 258 和 259 行调用main()函数:

# If vigenereHacker.py is run (instead of imported as a module), call
# the main() function:
if __name__ == '__main__':
    main()

这就是完整的维吉尼亚破解程序。是否成功取决于密文的特征。原始明文的字母频率越接近常规英语的字母频率，明文越长，破解程序就越有可能起作用。

修改破解程序的常量

如果破解程序不起作用，我们可以修改一些细节。我们在第 8 到 10 行设置的三个常量影响破解程序的运行方式:

MAX_KEY_LENGTH = 16 # Will not attempt keys longer than this.
NUM_MOST_FREQ_LETTERS = 4 # Attempt this many letters per subkey.
SILENT_MODE = False # If set to True, program doesn't print anything.

如果维吉尼亚密钥比第 8 行MAX_KEY_LENGTH中的整数长，破解程序将无法找到正确的密钥。如果破解程序未能破解密文，请尝试增加该值并再次运行该程序。

请记住，尝试破解一个不正确的短密钥长度需要很短的时间。但是，如果MAX_KEY_LENGTH设置得非常高，并且kasiskiExamination()函数错误地认为密钥长度可能是一个巨大的整数，程序可能会花费几个小时，甚至几个月的时间，试图使用错误的密钥长度破解密文。

为了防止这种情况，第 9 行的NUM_MOST_FREQ_LETTERS限制了每个子密钥尝试的可能字母的数量。通过增加这个值，破解程序会尝试更多的密钥，如果freqAnalysis.englishFreqMatchScore()对于原始明文消息不准确，您可能需要这样做，但这也会导致程序变慢。并且将NUM_MOST_FREQ_LETTERS设置为26会导致程序完全跳过缩小每个子项的可能字母数！

对于MAX_KEY_LENGTH和NUM_MOST_FREQ_LETTERS来说，较小的值执行起来更快，但破解密码成功的可能性更小，而较大的值执行起来更慢，但成功的可能性更大。

最后，为了提高程序的速度，你可以在第 10 行设置SILENT_MODE到True，这样程序就不会浪费时间把信息打印到屏幕上。虽然您的计算机可以快速执行计算，但在屏幕上显示字符可能相对较慢。不打印信息的缺点是，在程序完全运行完之前，您不会知道程序运行得如何。

总结

破解维吉尼亚密码需要遵循几个详细的步骤。此外，破解程序的许多部分可能会失败:例如，用于加密的维吉尼亚密钥可能比MAX_KEY_LENGTH长，或者英语频率匹配函数收到的结果不准确，因为明文不符合正常的字母频率，或者明文中有太多字典文件中没有的单词，而isEnglish()没有将其识别为英语。

当您发现破解程序可能失败的不同方式时，您可以更改代码来处理这种情况。但是本书中的破解程序做得很好，将数十亿或数万亿个可能的密钥减少到仅仅数千个。

然而，有一个技巧可以让维吉尼亚尔密码在数学上无法破解，不管你的计算机有多强大，你的破解程序有多聪明。你将在第 21 章中了解到这个被称为一次性密码本的技巧。

练习题

练习题的答案可以在本书的网站www.nostarch.com/crackingcodes找到。

1. 什么是字典攻击？

2.卡西斯基对密文的检查揭示了什么？

3. 使用set()函数将列表值转换为设定值时会发生哪两种变化？

4. 如果spam变量包含['cat', 'dog', 'mouse', 'dog']，则该列表中有四项。从list(set(spam))返回的清单有多少项？

5. 下面的代码打印了什么？

   print('Hello', end='')
   print('World')
   

二十一、一次性密码本

原文：https://inventwithpython.com/cracking/chapter21.html

“我已经研究过一千次了，”沃特豪斯说，“我能想到的唯一解释是，他们正在将他们的信息转换成大的二进制数，然后将它们与其他大的二进制数组合在一起——很可能是一次性密码本。”“在这种情况下，你的项目是注定要失败的，”艾伦说，“因为你不能打破一次性密码本。”

——尼尔·斯蒂芬森， Cryptonomicon

在这一章中，你将了解到一个不可能破解的密码，无论你的计算机有多强大，你花了多少时间试图破解它，或者你是一个多么聪明的黑客。它被称为一次性密码本，好消息是我们不必编写新的程序来使用它！你在第 18 章中编写的维吉尼亚密码程序无需任何修改就可以实现这种密码。但是一次性密码板很不方便经常使用，所以它经常被保留给最高机密的信息。

本章涵盖的主题

不可破解的一次性密码本

两次性密码本是维吉尼亚密码

不可破解的一次性密码本

一次性密码本密码是一种维吉尼亚密码，当密钥满足以下条件时，它将变得无法破解:

1. 它正好与加密消息一样长。

2. 它是由真正随机的符号组成的。

3. 它只用于一次，不会再用于任何其他消息。

通过遵循这三条规则，你可以使你的加密信息免受任何密码分析者的攻击。即使有无限的计算能力，密码也无法破解。

一次性密码本的密钥被称为密码本,因为这些密钥曾经被印在纸上。在最上面的一张纸被使用后，它会被从便笺簿上撕下来，露出下一个要使用的密钥。通常，会生成一个大型的一次性密码本密钥列表并亲自共享，这些密钥会标记特定的日期。例如，如果我们在 10 月 31 日收到来自合作者的消息，我们只需浏览一次性密码本列表，以找到当天的相应密钥。

使密钥长度等于消息长度

为了理解为什么一次性密码是不可破解的，我们来考虑一下是什么使得常规的维吉尼亚密码容易受到攻击。回想一下，维吉尼亚密码破解程序通过使用频率分析来工作。但是，如果密钥与消息的长度相同，则每个明文字母的子密钥是唯一的，这意味着每个明文字母可以以相等的概率被加密成任何密文字母。

例如，要加密信息，如果你想在这里生存，你必须知道你的毛巾在哪里，我们去掉空格和标点符号，得到一个有 55 个字母的信息。要使用一次性密码本加密此消息，我们需要一个 55 个字母长的密钥。使用示例密钥kcqyzhepxautiqekxejmoretztzhtrwwqdylbttvejmedbsanybppxqik对字符串进行加密，会得到密文shomtdecqtilchzsixghyikdfnnmacewrzlghraqqvhzguerplbqc，如图 21-1 所示。

图 21-1：使用一次性密码本加密一个示例消息

现在想象一个密码分析者得到了密文（SHOM TDEC...）.他们怎么能攻击密码呢？暴力破解密钥是行不通的，因为即使对计算机来说，密钥也太多了。密钥的数量将等于消息中字母总数的 26 次方。因此，如果在我们的示例中消息有 55 个字母，那么总共有26 ** 55，即 666091878431395624153823182526730590376250379528249805353030484209594192。

即使密码分析员有一台足够强大的计算机来尝试所有的密钥，它仍然无法破解一次性密码本，因为对于任何密文，所有可能的明文消息都有相同的概率。

例如，密文 SHOMTDEC…可以很容易地从完全不同的明文中得到相同长度的字母数，例如奥西里斯的神话在古埃及宗教中很重要，使用密钥zakavkxolfqdlzhwsqjbzmtwmmnakwuwerwexdcuywksgorghnnedvtcp加密，如图 21-2 所示。

图 21-2：使用不同的密钥对不同的示例消息进行加密，但产生与之前相同的密文

我们能够破解任何加密的原因是，我们知道通常只有一个密钥可以将信息解密成合理的英语。但是我们在前面的例子中已经看到，相同的密文可能是由两个完全不同的明文消息组成的。当我们使用一次性密码本时，密码分析者没有办法判断哪个是原始消息。事实上，任何长度正好为 55 个字母的可读的英语明文消息都有可能是原始明文。某个密钥能把密文解密成可读的英文，不代表它就是原来的加密密钥。

因为任何英文明文都可以被用来以相同的可能性创建密文，所以不可能破解使用一次性密码本加密的消息。

制作真正随机的密钥

正如你在第九章中了解到的，Python 内置的random模块并不产生真正的随机数。它们是用一种算法计算出来的，这种算法产生的数字看起来只是随机的，这在大多数情况下已经足够好了。然而，为了使一次性密码本起作用，密码本必须从真正随机的来源产生；否则，它就失去了数学上完美的保密性。

Python 3.6 和更高版本有secrets模块，它使用操作系统的真正随机数源（通常从随机事件中收集，比如用户击键之间的时间）。函数secrets. randbelow ()可以返回介于0和之间的真随机数，但不包括传递给它的参数，如下例所示:

>>> import secrets
>>> secrets.randbelow(10)
2
>>> secrets.randbelow(10)
0
>>> secrets.randbelow(10)
6

secrets中的函数比random中的函数慢，所以在不需要真随机性时，优先选择random中的函数。您还可以使用secrets.choice()函数，该函数从传递给它的字符串或列表中随机选择一个值，如下例所示:

>>> import secrets
>>> secrets.choice('ABCDEFGHIJKLMNOPQRSTUVWXYZ')
'R'
>>> secrets.choice(['cat', 'dog', 'mouse'])
'dog'

例如，要创建一个长度为 55 个字符的真正随机的一次性密码本，请使用以下代码:

>>> import secrets
>>> otp = ''
>>> for i in range(55):
        otp += secrets.choice('ABCDEFGHIJKLMNOPQRSTUVWXYZ')

>>> otp
'MVOVAAYDPELIRNRUZNNQHDNSOUWWNWPJUPIUAIMKFKNHQANIIYCHHDC'

使用一次性密码本时，我们还必须记住一个细节。让我们检查一下为什么我们需要避免多次使用同一个一次性密码本。

两次性密码本

两次性密码本密码是指使用同一个一次性密码本密钥对两个不同的消息进行加密。这造成了加密中的弱点。

如前所述，仅仅因为一个密钥将一次性密码本密文解密成可读的英文并不意味着它就是正确的密钥。然而，当你对两个不同的信息使用同一个密钥时，你就给了黑客重要的信息。如果您使用相同的密钥加密两条消息，而黑客找到了一个密钥，该密钥将第一条密文解密为可读的英语，但将第二条消息解密为随机垃圾文本，则黑客将知道他们找到的密钥一定不是原始密钥。事实上，很有可能只有一个密钥将两个消息都解密成英文，您将在下一节看到。

如果黑客只有两条消息中的一条，那条消息仍然是完全加密的。但是我们必须始终假设我们所有的加密信息都被黑客和政府截获了。否则，我们一开始就不会费心加密消息。记住香农的格言很重要:敌人了解系统！这包括你所有的密文。

为什么两次性密码本是维吉尼亚密码

你已经学会了如何破解维吉尼亚密码。如果我们可以证明两次填充密码和维吉尼亚密码是一样的，我们就可以用破解维吉尼亚密码的相同技术来证明它是可破解的。

为了解释为什么两次性密码本就像维吉尼亚密码一样是可破解的，让我们回顾一下维吉尼亚密码在加密长度超过密钥的消息时是如何工作的。当我们用完了密钥中用于加密的字母时，我们返回到密钥的第一个字母并继续加密。例如，要用 10 个字母的密钥（如YZNMPZXYXY）加密 20 个字母的消息（如BLUE IODINE INBOUND CAT）,前 10 个字母（BLUE IODINE）用YZNMPZXYXY加密，然后接下来的 10 个字母（INBOUND CAT）也用YZNMPZXYXY加密。图 21-3 显示了这种环绕效果。

图 21-3：维吉尼亚尔密码的环绕效应

使用一次性密码本密码，假设 10 个字母的消息BLUE IODINE是使用一次性密码本密钥YZNMPZXYXY加密的。然后密码学家错误地用相同的一次性密钥YZNMPZXYXY加密了第二个 10 个字母的消息INBOUND CAT，如图 21-4 所示。

图 21-4：使用一次性密码本密钥加密明文产生的密文与维吉尼亚密码相同。

当我们将图 21-3 (ZKHQXNAGKCGMOAJMAAXR）中所示的维吉尼亚密码的密文与图 21-4 (ZKHQXNAGKC GMOAJMAAXR）中所示的一次性密码的密文进行比较时，我们可以看到它们是完全相同的。这意味着，因为两次密码本密码与维吉尼亚密码具有相同的属性，所以我们可以使用相同的技术来破解它！

总结

简而言之，一次性密码本（one-time pad）是一种通过使用与消息长度相同、真正随机且仅使用一次的密钥来使维吉尼亚密码加密不受破解的方法。当这三个条件都满足时，一次性密码本就不可能破了。不过因为用起来太不方便了，所以没有用于日常加密。通常，一次性密码本会亲自分发，并包含一系列密钥。但要确保这份名单不会落入坏人之手！

练习题

练习题的答案可以在本书的网站www.nostarch.com/crackingcodes找到。

1. 为什么本章没有介绍一次性密码本程序？

2. 两次性密码本相当于哪个密码？

3. 使用两倍于明文消息长度的密钥会使一次性密码本加倍安全吗？

二十二、寻找和生成质数

原文：https://inventwithpython.com/cracking/chapter22.html

“数学家们至今都试图在质数序列中发现某种顺序，但却徒劳无功。我们有理由相信，这是一个人类思维永远无法深入的谜。”

——莱昂哈德·欧拉，18 世纪数学家

到目前为止，这本书描述的所有密码都已经存在了数百年。当黑客不得不依赖纸笔时，这些密码工作得很好，但现在它们更容易受到攻击，因为计算机处理数据的速度比人快几万亿倍。这些经典密码的另一个问题是它们使用相同的密钥进行加密和解密。当您试图发送加密的消息时，使用一个密钥会导致问题:例如，如何安全地发送密钥来解密它？

在第 23 章中，你将了解公钥密码如何通过使用非常大的质数来创建两个密钥来改进旧密码:一个用于加密的公钥和一个用于解密的私钥。要为公钥密码的密钥生成质数，您需要了解使密码成为可能的质数的一些属性（以及分解大数的难度）。在这一章中，你将利用质数的这些特性来创建primeNum.py模块，它可以通过快速判断一个数是否是质数来生成密钥。

本章涵盖的主题

质数和合数

试验部门素性测试

厄拉多塞的筛子

拉宾-米勒素性检验

什么是质数？

一个质数是大于 1 的整数，只有两个因子:1 和它本身。回想一下，一个数的因数是那些可以乘以等于原始数的数。例如，数字 3 和 7 是 21 的因数。数字 12 有因数 2 和 6，也有因数 3 和 4。

每个数字都有 1 和它自身的因数，因为 1 乘以任何数字都等于那个数字。例如，1 和 21 是 21 的因数，数字 1 和 12 是 12 的因数。如果一个数没有其他因子，这个数就是质数。例如，2 是一个质数，因为它只有 1 和 2 两个因子。

这里有一个简短的质数列表（注意 1 不被认为是质数）:2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97，101，103，107，109，113，127，131，137，139

质数有无穷多个，也就是说不存在最大质数这种东西。它们继续变得越来越大，就像普通的数字一样。公钥密码使用大质数使密钥变得太大而无法暴力破解。

质数可能很难找到，而大质数，如用于公钥的质数，就更难找到了。为了生成大质数作为公钥，我们将找到一个随机的大数，然后通过使用素性测试来检查该数是否是质数。如果根据质数测试，这个数是质数，我们就用它；否则，我们将继续创造和测试大数，直到我们找到一个质数。

让我们看一些非常大的数字来说明公钥密码中使用的质数可以有多大。

A googol是 10 的 100 次方，写成 1 后面跟 100 个零:

10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000

十亿十亿个古戈尔比一个古戈尔多 27 个零:

10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000

但是与公钥密码使用的质数相比，这些都是很小的数字。例如，公钥程序中使用的典型质数有数百位，可能如下所示:

112,829,754,900,439,506,175,719,191,782,841,802,172,556,768,
253,593,054,977,186,2355,84,979,780,304,652,423,405,148,425,
447,063,090,165,759,070,742,102,132,335,103,295,947,000,718,
386,333,756,395,799,633,478,227,612,244,071,875,721,006,813,
307,628,061,280,861,610,153,485,352,017,238,548,269,452,852,
733,818,231,045,171,038,838,387,845,888,589,411,762,622,041,
204,120,706,150,518,465,720,862,068,595,814,264,819

这个数字太大了，我打赌你甚至没有注意到里面的错别字。

了解质数的其他一些有趣的特征也是很有用的。因为所有的偶数都是 2 的倍数，所以 2 是唯一可能的偶数质数。同样，将两个质数相乘应该得到一个只有 1、它本身和被相乘的两个质数的因数的数。（例如，质数 3 和 7 相乘得到 21，其唯一的因子是 1、21、3 和 7。）

不是质数的整数被称为合数，因为它们至少由 1 和数字之外的两个因子组成。每个合数都有一个质因数分解，这是一个只由质数组成的因数分解。比如合数 1386 是由质数 2、3、7、11 组成的，因为2 × 3 × 3 × 7 × 11 = 1386。每个合数的质因数分解对于该合数是唯一的。

我们将使用这些关于什么使一个数成为质数的信息来编写一个模块，这个模块可以确定一个小数是否是质数并生成质数。模块primeNum.py将定义以下函数:

isPrimeTrialDiv()：如果传递给它的数是质数，则使用试除法算法返回True，如果传递给它的数不是质数，则返回False。

primeSieve()：使用厄拉多塞算法的筛子来生成质数。

rabinMiller()：使用 Rabin-Miller 算法检查传递给它的数字是否是质数。与试除法算法不同，该算法可以快速处理非常大的数字。该函数不是直接调用，而是由isPrime()调用。

isPrime()：在用户必须判断一个大整数是否为质数时调用。

generateLargePrime()：返回一个数百位长的大质数。该函数将在第 23 章的makePublicPrivateKeys.py程序中使用。

primeNum模块的源代码

就像第 13 章中介绍的cryptomath.py一样，primeNum.py程序是作为一个模块被其他程序导入的，当它自己运行时不做任何事情。primeNum.py模块导入 Python 的math和random模块，以便在生成质数时使用。

选择文件 -> 新文件，打开新文件编辑器窗口。在文件编辑器中输入以下代码，然后保存为primeNum.py。

primeNum.py

# Prime Number Sieve
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)

import math, random


def isPrimeTrialDiv(num):
    # Returns True if num is a prime number, otherwise False.

    # Uses the trial division algorithm for testing primality.

    # All numbers less than 2 are not prime:
    if num < 2:
        return False

    # See if num is divisible by any number up to the square root of num:
    for i in range(2, int(math.sqrt(num)) + 1):
        if num % i == 0:
            return False
    return True


def primeSieve(sieveSize):
    # Returns a list of prime numbers calculated using
    # the Sieve of Eratosthenes algorithm.

    sieve = [True] * sieveSize
    sieve[0] = False # Zero and one are not prime numbers.
    sieve[1] = False

    # Create the sieve:
    for i in range(2, int(math.sqrt(sieveSize)) + 1):
        pointer = i * 2
        while pointer < sieveSize:
            sieve[pointer] = False
            pointer += i

    # Compile the list of primes:
    primes = []
    for i in range(sieveSize):
        if sieve[i] == True:
            primes.append(i)

    return primes

def rabinMiller(num):
    # Returns True if num is a prime number.
    if num % 2 == 0 or num < 2:
        return False # Rabin-Miller doesn't work on even integers.
    if num == 3:
        return True
    s = num - 1
    t = 0
    while s % 2 == 0:
        # Keep halving s until it is odd (and use t
        # to count how many times we halve s):
        s = s // 2
        t += 1
    for trials in range(5): # Try to falsify num's primality 5 times.
        a = random.randrange(2, num - 1)
        v = pow(a, s, num)
        if v != 1: # This test does not apply if v is 1.
            i = 0
            while v != (num - 1):
                if i == t - 1:
                    return False
                else:
                    i = i + 1
                    v = (v ** 2) % num
    return True

# Most of the time we can quickly determine if num is not prime
# by dividing by the first few dozen prime numbers. This is quicker
# than rabinMiller() but does not detect all composites.
LOW_PRIMES = primeSieve(100)


def isPrime(num):
    # Return True if num is a prime number. This function does a quicker
    # prime number check before calling rabinMiller().
    if (num < 2):
        return False # 0, 1, and negative numbers are not prime.

    # See if any of the low prime numbers can divide num:

    for prime in LOW_PRIMES:

        if (num == prime):

            return True

        if (num % prime == 0):

            return False

    # If all else fails, call rabinMiller() to determine if num is prime:
    return rabinMiller(num)


def generateLargePrime(keysize=1024):
    # Return a random prime number that is keysize bits in size:
    while True:
        num = random.randrange(2**(keysize-1), 2**(keysize))
        if isPrime(num):
            return num

primeNum模块的示例运行

要查看primeNum.py模块的示例输出，请在交互式 shell 中输入以下内容:

>>> import primeNum
>>> primeNum.generateLargePrime()
122881168342211041030523683515443239007484290600701555369488271748378054744009
463751312511471291011945732413378446666809140502037003673211052153493607681619
990563076859566835016382556518967124921538212397036345815983641146000671635019
637218348455544435908428400192565849620509600312468757953899553441648428119
>>> primeNum.isPrime(45943208739848451)
False
>>> primeNum.isPrime(13)
True

导入primeNum.py模块让我们可以使用generateLargePrime()函数生成一个非常大的质数。它还允许我们将任何数字，无论大小，传递给isPrime()函数来确定它是否是一个质数。

试除法算法如何工作

为了找出一个给定的数是否是质数，我们使用试除法算法。该算法继续将一个数除以整数（从 2、3 等开始），以查看是否有任何整数以 0 为余数将该数整除。例如，为了测试 49 是否是质数，我们可以尝试用 2 开始的整数来除它:

49 ÷ 2 = 24 ... 1
49 ÷ 3 = 16 ... 1
49 ÷ 4 = 12 ... 1
49 ÷ 5 = 9 ... 4
49 ÷ 6 = 8 ... 1
49 ÷ 7 = 7 ... 0

因为 7 除以 49 的余数为 0，所以我们知道 7 是 49 的因数。这意味着 49 不可能是质数，因为它至少有 1 和它本身之外的一个因子。

我们可以通过只除以质数而不是合数来加快这个过程。如前所述，合数无非是质数的合成。这意味着，如果 2 不能将 49 整除，那么一个合数，比如 6，它的因子包括 2，也不会能够将 49 整除。换句话说，任何被 6 整除的数也可以被 2 整除，因为 2 是 6 的因数。图 22-1 说明了这个概念。

图 22-1：任何被 6 整除的数也被 2 整除。

再举个例子，我们来测试一下 13 是不是质数:

13 ÷ 2 = 6 ... 1
13 ÷ 3 = 4 ... 1

我们只需要测试整数到（包括）我们测试的质数的平方根。一个数的平方根指的是与自身相乘得到那个原始数的数。比如 25 的平方根是 5，因为5 × 5 = 25。因为一个数不能有两个大于其平方根的因子，所以我们可以将试除法算法测试限制在小于该数平方根的整数上。13 的平方根大约是 3.6，所以我们只需要除以 2 和 3 就可以确定 13 是质数。

作为另一个例子，数字 16 的平方根是 4。两个大于 4 的数相乘总会得到一个大于 16 的数，任何大于 4 的 16 的因子总会与小于 4 的因子配对，比如 8 × 2。因此，通过查找任何小于平方根的因子，您将找到所有大于平方根的因子。

要在 Python 中找到一个数的平方根，可以使用math.sqrt()函数。在交互式 shell 中输入以下内容，查看该函数如何工作的一些示例:

>>> import math
>>> 5 * 5
25
>>> math.sqrt(25)
5.0
>>> math.sqrt(10)
3.1622776601683795

注意math.sqrt()总是返回一个浮点值。

实现试除法算法测试

primeNum.py中第 7 行的isPrimeTrialDiv()函数以一个数为参数num，用试除法算法测试，检查该数是否为质数。如果num是一个合数，函数返回False，如果num是一个质数，函数返回True。

def isPrimeTrialDiv(num):
    # Returns True if num is a prime number, otherwise False.

    # Uses the trial division algorithm for testing primality.

    # All numbers less than 2 are not prime:
    if num < 2:
        return False

第 13 行检查num是否小于2，如果是，函数返回False，因为小于 2 的数不能是质数。

第 17 行开始了实现试除法算法的for循环。它还使用math.sqrt()得到num的平方根，并使用返回的浮点值来设置我们将测试的整数范围的上限。

    # See if num is divisible by any number up to the square root of num:
    for i in range(2, int(math.sqrt(num)) + 1):
        if num % i == 0:
            return False
    return True

第 18 行使用模运算符（%）检查余数是否为 0。如果余数为 0，num可被i整除，因此不是质数，循环返回False。如果第 17 行上的for循环没有返回False，则该函数返回第 20 行上的True以指示num可能是质数。

函数isPrimeTrialDiv()中的试除法算法很有用，但它不是测试素性的唯一方法。你也可以用厄拉多塞筛找到质数。

厄拉多塞的筛子

厄拉多塞的筛子（发音为“era-taws-thuh-knees”）是一种算法，可以找到一个数字范围内的所有质数。为了了解这个算法是如何工作的，想象一组盒子。每个盒子里装的是从 1 到 50 的整数，都标为质数，如图 22-2 所示。

为了实现厄拉多塞筛，我们从我们的范围中排除非质数，直到只剩下质数。因为 1 从来不是质数，所以让我们先把数字 1 标为“不是质数”那我们就把所有 2 的倍数（除了 2）都标为“不是质数。”这意味着我们将把整数 4（2 × 2）、6（2 × 3）、8（2 × 4）、10、12 等等直到 50 标记为“非质数”，如图 22-3 所示。

图 22-2：为数字 1 到 50 设置厄拉多塞筛

图 22-3：消除数字 1 和所有偶数

然后，我们使用 3 的倍数重复这个过程:我们排除 3，并将 6、9、12、15、18、21 等标记为“非质数”我们对不包括 4 的 4 的倍数、不包括 5 的 5 的倍数等等重复这个过程，直到我们得到 8 的倍数。我们停在 8，因为它大于 7.071，7.071 是 50 的平方根。所有 9、10、11 等等的倍数都已经被标记出来了，因为任何一个比平方根大的因数都会和一个比平方根小的因数配对，我们已经标记过了。

完成的筛子应该看起来像图 22-4 ，质数显示在白色方框中。

图 22-4：用厄拉多塞的筛子找到质数

利用厄拉多塞的筛子，我们发现小于 50 的质数是 2，3，5，7，11，13，17，19，23，29，31，37，41，43，47。当您想要快速找到某个数字范围中的所有质数时，最好使用这种筛选算法。这比以前用试除法算法逐个检查每个数要快得多。

用厄拉多塞筛生成质数

primeNum.py模块第 23 行的primeSieve()函数使用厄拉多塞算法的筛子返回一个在1和sieveSize之间的所有质数的列表:

def primeSieve(sieveSize):
    # Returns a list of prime numbers calculated using
    # the Sieve of Eratosthenes algorithm.

    sieve = [True] * sieveSize
    sieve[0] = False # Zero and one are not prime numbers.
    sieve[1] = False

第 27 行创建了表示sieveSize长度的布尔True值列表。因为0和1不是质数，所以0和1索引被标记为False。

第 32 行的for循环遍历从2到sieveSize的平方根的每个整数:

    # Create the sieve:
    for i in range(2, int(math.sqrt(sieveSize)) + 1):
        pointer = i * 2
        while pointer < sieveSize:
            sieve[pointer] = False
            pointer += i

变量pointer从i后i的第一个倍数开始，也就是第 33 行的i * 2。然后while循环将sieve列表中的pointer索引设置为False，第 36 行将pointer改为指向i的下一个倍数。

在第 32 行的for循环结束后，sieve列表现在应该包含每个质数索引的True。我们创建一个新的列表，它在primes中以一个空列表开始，遍历整个sieve列表，当sieve[i]是True或i是质数时追加数字:

    # Compile the list of primes:
    primes = []
    for i in range(sieveSize):
        if sieve[i] == True:
            primes.append(i)

第 44 行返回质数列表:

    return primes

primeSieve()函数可以找到小范围内的所有质数，isPrimeTrialDiv()函数可以快速判断一个小数字是否是质数。但是一个几百位数的大整数呢？

如果我们将一个大整数传递给isPrimeTrialDiv()，需要几秒钟来判断它是否是质数。如果这个数有几百位数长，就像我们将在第 23 章中的公钥密码程序中使用的质数一样，要花一万多亿年才能算出这个数是否是质数。

在下一节中，您将学习如何使用 Rabin-Miller 素性测试来确定一个非常大的数是否是质数。

拉宾-米勒素性算法

Rabin-Miller 算法的主要优点是，它是一个相对简单的素性测试，在普通计算机上运行只需几秒钟。尽管该算法的 Python 代码只有几行，但对其工作原理的数学证明的解释对于本书来说太长了。Rabin-Miller 算法不是素性的可靠测试。相反，它找到很可能是质数但不保证是质数的数字。但是假阳性的几率很小，这种方法对于本书来说已经足够好了。要了解更多关于拉宾-米勒算法的工作原理，你可以在en.wikipedia.org/wiki/Miller%E2%80%93Rabin_primality_test阅读。

*rabinMiller()函数实现这个算法来寻找质数:

def rabinMiller(num):
    # Returns True if num is a prime number.
    if num % 2 == 0 or num < 2:
        return False # Rabin-Miller doesn't work on even integers.
    if num == 3:
        return True
    s = num - 1
    t = 0
    while s % 2 == 0:
        # Keep halving s until it is odd (and use t
        # to count how many times we halve s):
        s = s // 2
        t += 1
    for trials in range(5): # Try to falsify num's primality 5 times.
        a = random.randrange(2, num - 1)
        v = pow(a, s, num)
        if v != 1: # This test does not apply if v is 1.
            i = 0
            while v != (num - 1):
                if i == t - 1:
                    return False
                else:
                    i = i + 1
                    v = (v ** 2) % num
    return True

不要担心这段代码是如何工作的。要记住的重要概念是，如果rabinMiller()函数返回True，那么num参数很可能是质数。如果rabinMiller()返回False，num肯定是复合的。

寻找大质数

我们将创建另一个名为isPrime()的函数来调用rabinMiller()。拉宾-米勒算法并不总是检验一个数是否是质数的最有效的方法；因此，在isPrime()函数的开始，我们将做一些简单的检查，作为判断存储在参数num中的数字是否是质数的捷径。让我们在常量变量LOW_PRIMES中存储一个所有小于 100 的质数的列表。我们可以用primeSieve ()函数来计算这个列表:

    # Most of the time we can quickly determine if num is not prime
    # by dividing by the first few dozen prime numbers. This is quicker
    # than rabinMiller() but does not detect all composites.
    LOW_PRIMES = primeSieve(100)

我们将像在isPrimeTrialDiv()中一样使用这个列表，并忽略任何小于 2 的数字（第 81 行和第 82 行）:

def isPrime(num):
    # Return True if num is a prime number. This function does a quicker
    # prime number check before calling rabinMiller().
    if (num < 2):
        return False # 0, 1, and negative numbers are not prime.

当num不小于2时，我们也可以使用LOW_PRIMES列表作为测试num的快捷方式。检查num是否能被所有小于 100 的质数整除不会明确地告诉我们这个数是否是质数，但它可能帮助我们找到合数。通过除以小于 100 的质数，大约 90% 传递给isPrime()的大整数可以被检测为复合整数。原因是，如果一个数能被一个质数，比如 3，整除，就不用检查这个数是否能被合数 6，9，12，15，或者其他任何 3 的倍数整除。用较小的质数除这个数比对这个数执行较慢的 Rabin-Miller 算法要快得多，所以这个快捷方式有助于程序在调用isPrime()的 90% 的时间里执行得更快。

第 85 行循环遍历LOW_PRIMES列表中的每个质数:

    # See if any of the low prime numbers can divide num:
    for prime in LOW_PRIMES:
        if (num == prime):
            return True87.         if (num % prime == 0):
            return False

如果num中的整数与prime相同，那么显然num必须是质数，第 86 行返回True。num中的整数由每个质数使用第 87 行上的模运算符进行调制，如果结果求值为0，我们知道prime除以num所以num不是质数。在这种情况下，第 88 行返回False。

这是我们将执行的三个快速测试，以确定一个数是否是质数。如果执行继续超过第 87 行，rabinMiller()函数检查num的素性。

第 90 行调用rabinMiller()函数判断数字是否为质数；然后，rabinMiller()函数获取它的返回值，并从isPrime()函数返回:

    # If all else fails, call rabinMiller() to determine if num is prime:
    return rabinMiller(num)

现在你知道如何确定一个数是否是质数，我们将使用这些质数测试来生成质数。这些将由第 23 章中的公钥程序使用。

生成大质数

使用无限循环，第 93 行的generateLargePrime()函数返回一个质数整数。它通过生成一个大随机数，将其存储在num中，然后将num传递给isPrime()来实现这一点。然后，isPrime()函数测试num是否是质数。

def generateLargePrime(keysize=1024):
    # Return a random prime number that is keysize bits in size:
    while True:
        num = random.randrange(2**(keysize-1), 2**(keysize))
        if isPrime(num):
            return num

如果num是质数，第 98 行返回num。否则，无限循环返回到第 96 行以尝试新的随机数。这个循环继续下去，直到找到一个被isPrime()函数确定为质数的数字。

generateLargePrime()函数的keysize参数的默认值为1024。keysize越大，可能的密钥就越多，密码就越难被暴力破解。公钥的大小通常是以称为位的数字来计算的，你将在第 23 章和第 24 章中了解更多。就目前而言，只需要知道 1024 位的数字非常大:大约 300 位数！

总结

质数在数学中有迷人的性质。正如你将在第 23 章中了解到的，它们也是专业加密软件中使用的密码的支柱。质数的定义很简单:它是一个只有 1 和它自己作为因子的数。但是确定哪些数字是质数需要一些聪明的代码。

在这一章中，我们编写了isPrimeTrialDiv()函数来判断一个数是否是质数，方法是用 2 和这个数的平方根之间的所有数来修改一个数。这是试除法算法。当一个质数由除了它的因子 1 和它本身之外的任何数构成时，它的余数不应该是 0。所以我们知道余数为 0 的数不是质数。

你知道了厄拉多塞的筛子可以快速找到一个数字范围内的所有质数，尽管它在寻找大质数时使用了太多的内存。

因为厄拉多塞的筛子和primeNum.py中的试除法算法不足以快速找到大质数，所以我们需要另一种公钥密码算法，它使用数百位长的超大质数。作为一种变通方法，您学会了使用 Rabin-Miller 算法，该算法使用复杂的数学推理来确定一个非常大的数是否是质数。

在第 23 章中，你将使用primeNum.py模块编写公钥密码程序。最后，您将创建一个比一次性密码更容易使用的密码，但不会被本书中介绍的简单黑客技术破解！

练习题

练习题的答案可以在本书的网站www.nostarch.com/crackingcodes找到。

1. 有多少质数？

2. 什么叫非质数的整数？

3. 求质数的两种算法是什么？

二十三、生成公钥密码的密钥

原文：https://inventwithpython.com/cracking/chapter23.html

“使用故意妥协的加密技术，它有一个后门，只有‘好人’才有密钥，你实际上没有安全保障。你还不如用预先破解的、被破坏的加密方法来加密它。”

——科利·多克托罗，科幻小说作者，2015

到目前为止，你在本书中学到的所有密码都有一个共同的特点:加密密钥与解密密钥相同。这就引出了一个棘手的问题:如何与一个你从未交谈过的人分享加密信息？任何窃听者都可以截取你发送的加密密钥，就像他们截取加密信息一样容易。

在本章中，您将学习公钥加密，它允许陌生人使用公钥和私钥共享加密的消息。您将了解公钥密码，在本书中，它是基于 RSA 密码的。因为 RSA 密码很复杂，涉及多个步骤，所以您将编写两个程序。在本章中，您将编写公钥生成程序来生成您的公钥和私钥。然后，在第 24 章中，您将编写第二个程序，使用公钥密码并应用这里生成的密钥来加密和解密消息。在我们深入研究这个程序之前，让我们先来探索一下公钥加密是如何工作的。

本章涵盖的主题

公钥加密

认证

数字签名

MITM 袭击

生成公钥和私钥

混合密码系统

公钥加密

想象一下，在世界的另一端有人想和你交流。你们都知道间谍机构在监控所有的电子邮件、字母、短信和电话。要向此人发送加密邮件，双方必须就使用的密钥达成一致。但是，如果你们中的一个人用电子邮件把密钥发给另一个人，间谍机构就会截获这个密钥，然后解密任何用这个密钥加密的信息。私下见面交换密钥是不可能的。你可以试着加密密钥，但这需要将该消息的秘密密钥发送给其他人，这也会被拦截。

公钥加密通过使用两个密钥来解决这个加密问题，一个用于加密，一个用于解密，是非对称密码的一个例子。像本书之前的许多密码一样，使用相同密钥进行加密和解密的密码是对称密码。

重要的是要知道使用加密密钥（公钥）加密的消息只能使用解密密钥（私钥）解密。因此，即使有人获得了加密密钥，他们也无法读取原始消息，因为加密密钥无法解密消息。

加密密钥被称为公钥，因为它可以与全世界共享。相比之下，私钥，或解密密钥，必须保密。

例如，如果 Alice 想给 Bob 发送一条消息，Alice 找到 Bob 的公钥，或者 Bob 可以把它给她。然后，Alice 使用 Bob 的公钥加密她给 Bob 的消息。因为公钥不能解密消息，所以其他每个人都可以访问 Bob 的公钥并不重要。

当 Bob 收到 Alice 的加密消息时，他使用自己的私钥对其进行解密。只有 Bob 有私钥，可以解密用他的公钥加密的消息。如果 Bob 想要回复 Alice，他会找到她的公钥并用它来加密他的回复。因为只有爱丽丝知道她的私钥，所以爱丽丝是唯一能够解密来自鲍勃的加密响应的人。即使爱丽丝和鲍勃在世界的两端，他们也可以交换信息而不用担心被拦截。

我们将在本章中实现的特定公钥密码是基于 RSA 密码的，RSA 密码发明于 1977 年，并以其发明者的姓氏首字母命名:罗恩·里维斯特、阿迪·萨莫尔和伦纳德·阿德曼。

RSA 密码在其算法中使用数百位长的大质数。这就是我们在第 22 章中讨论质数数学的原因。公钥算法创建两个随机的质数，然后使用复杂的数学（包括寻找一个模逆，你在第 13 章中学会了如何做）来创建公钥和私钥。

使用教科书 RSA 的危险

尽管我们在本书中没有编写一个程序来破解公钥密码程序，但是请记住，你将在第 24 章中编写的publicKeyCipher.py程序不是安全的。获得正确的加密是非常困难的，并且需要大量的经验才能知道一个密码（以及实现它的程序）是否真正安全。

本章中基于 RSA 的程序被称为教科书 RSA ，因为即使它在技术上使用大质数正确地实现了 RSA 算法，它也容易受到破解。例如，使用伪随机而不是真正的随机数生成函数会使密码变得脆弱，正如你在第 22 章中了解到的，拉宾-米勒素性测试不能保证总是正确的。

因此，尽管你可能无法破解由publicKeyCipher.py创建的密文，但其他人可能可以。套用高度成功的密码学家 Bruce Schneier 的话，任何人都可以创建自己无法破解的密码算法。具有挑战性的是创建一个其他人无法破解的算法，即使经过多年的分析。本书中的程序只是一个有趣的例子，旨在教你 RSA 密码的基础知识。但是一定要使用专业的加密软件来保护你的文件。你可以在www.nostarch.com/crackingcodes找到一份（通常是免费的）加密软件清单。

认证的问题

尽管公钥密码听起来很巧妙，但还是有一个小问题。比如，想象你收到了这封邮件:“你好。我是爱麦虞埃尔·果尔德施坦因，反抗军的领袖。我想和你秘密地交流一些重要的事情。附上我的公钥。”

使用此公钥，您可以确保您发送的消息不会被除公钥发送者之外的任何人阅读。但是你怎么知道发信人实际上是爱麦虞埃尔·果尔德施坦因呢？你不知道你是在向爱麦虞埃尔·果尔德施坦因发送加密信息，还是在向一个伪装成爱麦虞埃尔·果尔德施坦因的间谍机构发送信息，来引诱你进入陷阱！

尽管公钥密码，事实上，本书中的所有密码都可以提供保密性（对消息保密），但它们并不总是提供认证（证明你与之通信的人就是他们所说的那个人）。

通常，这对于对称密码来说不是问题，因为当你和一个人交换密钥时，你可以看到那个人是谁。然而，当您使用公钥加密时，您不需要见到某人就可以获得他们的公钥并开始向他们发送加密的消息。当您使用公钥加密时，要记住身份验证是至关重要的。

一个名为公钥基础设施（PKI） 的完整字段管理认证，因此您可以将公钥与具有某种安全级别的人进行匹配；然而，这个话题超出了本书的范围。

数字签名

数字签名允许您使用加密技术对文档进行电子签名。为了理解为什么数字签名是必要的，让我们看看下面的例子，Alice 给 Bob 的电子邮件:

亲爱的鲍勃:

我答应用一百万美元买下你的旧笔记本电脑。

真诚地

爱丽丝

这对鲍勃来说是个好消息，因为他想不惜任何代价处理掉他那毫无价值的笔记本电脑。但是，如果爱丽丝后来声称她没有做出这个承诺，鲍勃收到的电子邮件是假的，她没有发送。毕竟，Bob 可以轻松创建这封电子邮件。

如果他们见面，爱丽丝和鲍勃可以简单地签署一份同意出售的合同。手写签名不那么容易伪造，并且提供了一些证据证明爱丽丝确实做出了这个承诺。但是，即使爱丽丝签署了这样的合同，用她的数码相机拍了照片，并把图像文件发送给鲍勃，仍然可以想象图像可能被修改过。

RSA 密码（像其他公钥密码一样）不仅加密消息，还允许我们对文件或字符串进行数字签名。例如，Alice 可以使用她的私钥加密消息，生成只有 Alice 的公钥才能解密的密文。该密文成为文件的数字签名。它实际上并不是一个秘密，因为世界上的每个人都可以使用 Alice 的公钥来解密它。但是通过用她的私钥加密信息，爱丽丝可以用一种无法伪造的方式对信息进行数字签名。 因为只有爱丽丝能接触到她的私钥，只有爱丽丝才有可能产生这个密文，她不能说是鲍勃伪造或者篡改的！

保证已经创作了一条消息的人不能在以后否认该消息的创作被称为不可否认性。

人们在许多重要活动中使用数字签名，包括加密货币、公钥认证和匿名网上冲浪。要了解更多信息，请前往www.nostarch.com/crackingcodes。请继续阅读，了解为什么身份验证与安全加密一样重要。

当心 MITM 攻击

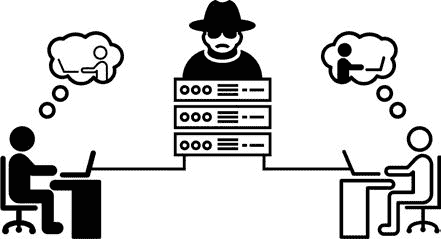
比有人入侵我们的加密信息更阴险的是中间人或中间人（MITM）攻击。在这种类型的攻击中，有人截获了你的消息，并在你不知情的情况下传递出去。例如，假设爱麦虞埃尔·果尔德施坦因真的想和你通信，并用他的公钥给你发送了一条未加密的消息，但是间谍机构的路由器截获了这条消息。代理机构可以用自己的公钥替换电子邮件附带的公钥 Emmanuel，然后将消息发送给您。你不可能知道你收到的密钥是艾曼纽的还是间谍机构的！

然后当你加密给 Emmanuel 的回复时，你实际上是用间谍机构的公钥加密，而不是 Emmanuel 的公钥。间谍机构将能够截获该消息，解密并阅读它，然后在把你的消息发送给 Emmanuel 之前，用 Emmanuel 的实际公钥重新加密它。该机构可以对 Emmanuel 发送给您的任何回复进行同样的处理。图 23-1 显示了 MITM 攻击是如何运作的。

图 23-1：一次 MITM 攻击

对你和艾曼纽来说，看起来你们在秘密地交流。但是间谍机构正在阅读你所有的信息，因为你和伊曼纽尔正在用间谍机构生成的公钥加密你的信息！同样，这个问题的存在是因为公钥密码只提供机密性，而不提供身份验证。对认证和公钥基础设施的深入讨论超出了本书的范围。但是现在您已经知道了公钥加密如何提供保密性，让我们来看看如何为公钥加密生成密钥。

生成公钥和私钥的步骤

公钥方案中的每个密钥都由两个数字组成。公钥将是两个数字n和e。私钥将是两个数字n和d。

创建这些数字的三个步骤如下:

1. 创建两个随机的、不同的、非常大的质数: p和q。将这两个数字相乘得到一个名为n的数字。

2. 创建一个随机数，叫做e，它与(p – 1) × (q – 1)互质。

3. 计算e的模逆，我们称之为d。

注意两个密钥中都使用了n。数字d必须保密，因为它可以解密信息。现在您已经准备好编写一个生成这些密钥的程序了。

公钥生成程序的源代码

选择文件 -> 新文件，打开新文件编辑器窗口。确保primeNum.py和cryptomath.py模块与程序文件在同一个文件夹中。在文件编辑器中输入以下代码，保存为makepublicprivatekeys.py。

makePublic
私钥. py

# Public Key Generator
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)

import random, sys, os, primeNum, cryptomath


def main():
    # Create a public/private keypair with 1024-bit keys:
    print('Making key files...')
    makeKeyFiles('al_sweigart', 1024)
    print('Key files made.')

def generateKey(keySize):
    # Creates public/private keys keySize bits in size.
    p = 0
    q = 0
    # Step 1: Create two prime numbers, p and q. Calculate n = p * q:
    print('Generating p prime...')
    while p == q:
        p = primeNum.generateLargePrime(keySize)
        q = primeNum.generateLargePrime(keySize)
    n = p * q

    # Step 2: Create a number e that is relatively prime to (p-1)*(q-1):
    print('Generating e that is relatively prime to (p-1)*(q-1)...')
    while True:
        # Keep trying random numbers for e until one is valid:
        e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
        if cryptomath.gcd(e, (p - 1) * (q - 1)) == 1:
            break

    # Step 3: Calculate d, the mod inverse of e:
    print('Calculating d that is mod inverse of e...')
    d = cryptomath.findModInverse(e, (p - 1) * (q - 1))

    publicKey = (n, e)
    privateKey = (n, d)

    print('Public key:', publicKey)
    print('Private key:', privateKey)

    return (publicKey, privateKey)


def makeKeyFiles(name, keySize):
    # Creates two files 'x_pubkey.txt' and 'x_privkey.txt' (where x
    # is the value in name) with the n,e and d,e integers written in
    # them, delimited by a comma.

    # Our safety check will prevent us from overwriting our old key files:
    if os.path.exists('%s_pubkey.txt' % (name)) or
          os.path.exists('%s_privkey.txt' % (name)):
        sys.exit('WARNING: The file %s_pubkey.txt or %s_privkey.txt
              already exists! Use a different name or delete these files and
              rerun this program.' % (name, name))

    publicKey, privateKey = generateKey(keySize)

    print()
    print('The public key is a %s and a %s digit number.' %
          (len(str(publicKey[0])), len(str(publicKey[1]))))
    print('Writing public key to file %s_pubkey.txt...' % (name))
    fo = open('%s_pubkey.txt' % (name), 'w')
    fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))
    fo.close()

    print()
    print('The private key is a %s and a %s digit number.' %
          (len(str(publicKey[0])), len(str(publicKey[1]))))
    print('Writing private key to file %s_privkey.txt...' % (name))
    fo = open('%s_privkey.txt' % (name), 'w')
    fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
    fo.close()


# If makePublicPrivateKeys.py is run (instead of imported as a module),
# call the main() function:
if __name__ == '__main__':
    main()

公钥生成程序的运行示例

当我们运行makePublicPrivateKeys.py程序时，输出应该类似如下（当然，您的密钥的数字看起来会不同，因为它们是随机生成的）:

Making key files...
Generating p prime...
Generating q prime...
Generating e that is relatively prime to (p-1)*(q-1)...
Calculating d that is mod inverse of e...
Public key: (210902406316700502401968491406579417405090396754616926135810621
2161161913380865678407459875355468897928072386270510720443827324671435893274
8583937496850624116776147241821152026946322876869404394483922202407821672864
2424789208131826990008473526711744296548563866768454251404951960805224682425
498975230488955908086491852116348777849536270685085446970952915640050522212
204221803744494065881010331486468305317449607027884787770315729959789994713
265311327663776167710077018340036668306612665759417207845823479903440572724
068125211002329298338718615859542093721097258263595617482450199200740185492
04468791300114315056117093, 17460230769175161021731845459236833553832403910869
129054954200373678580935247606622265764388235752176654737805849023006544732896
308685513669509917451195822611398098951306676600958889189564599581456460070270
393693277683404354811575681605990659145317074127084557233537504102479937142530
0216777273298110097435989)
Private key: (21090240631670050240196849140657941740509039675461692613581062
1216116191338086567840745987535546889792807238627051072044382732467143589327
4858393749685062411677614724182115202694632287686940439448392220240782167286
4242478920813182699000847352671174429654856386676845425140495196080522468242
5498975230488955908086491852116348777849536270685085446970952915640050522212
204221803744494065881010331486468305317449607027884787770315729959789994713
265311327663776167710077018340036668306612665759417207845823479903440572724
068125211002329298338718615859542093721097258263595617482450199200740185492
04468791300114315056117093, 47676735798137710412166884916983765043173120289416
904341295971552286870991874666099933371008075948549008551224760695942666962465
968168995404993934508399014283053710676760835948902312888639938402686187075052
360773062364162664276144965652558545331166681735980981384493349313058750259417
68372702963348445191139635826000818122373486213256488077192893119257248107794
25681884603640028673273135292831170178614206817165802812291528319562200625082
55726168047084560706359601833919317974375031636011432177696164717000025430368
26990539739057474642785416933878499897014777481407371328053001838085314443545
845219087249544663398589)
The public key is a 617 and a 309 digit number.
Writing public key to file al_sweigart_pubkey.txt...
The private key is a 617 and a 309 digit number.
Writing private key to file al_sweigart_privkey.txt...

因为这两个密钥非常大，所以它们都被写入各自的文件中，al_sweigart_pubkey.txt和al_sweigart_privkey.txt。我们将在第 24 章的公钥密码程序中使用这两个文件来加密和解密消息。这些文件名来自字符串'al_sweigart'，它被传递给程序第 10 行的makeKeyFiles()函数。您可以通过传递不同的字符串来指定不同的文件名。

如果我们再次运行makePublicPrivateKeys.py并将相同的字符串传递给makeKeyFiles()，程序的输出应该是这样的:

Making key files...
WARNING: The file al_sweigart_pubkey.txt or al_sweigart_privkey.txt already
exists! Use a different name or delete these files and rerun this program.

提供此警告是为了防止我们意外地覆盖我们的密钥文件，这将使任何用它们加密的文件无法恢复。一定要保管好这些密钥文件！

创建main()函数

当我们运行makePublicPrivateKeys.py时，main()函数被调用，它使用makeKeyFiles()函数创建公钥和私钥文件，我们将很快定义这个函数。

def main():
    # Create a public/private keypair with 1024-bit keys:
    print('Making key files...')
    makeKeyFiles('al_sweigart', 1024)
    print('Key files made.')

因为计算机可能需要一段时间来生成密钥，所以我们在调用makeKeyFiles()之前在第 9 行打印一条消息，让用户知道程序正在做什么。

第 10 行的makeKeyFiles()调用传递字符串'al_sweigart'和整数1024，生成 1024 位的密钥并存储在文件al_sweigart_pubkey.txt和al_sweigart_privkey.txt中。密钥越大，可能的密钥就越多，密码的安全性就越强。但是，大密钥意味着加密或解密消息需要更长的时间。对于本书的例子，我选择 1024 位的大小作为速度和安全性之间的平衡；但实际上，2048 位甚至 3072 位的密钥大小对于安全公钥加密是必要的。

使用generateKey()函数生成密钥

创建密钥的第一步是产生两个随机质数p和q。这些数字必须是两个大而不同的质数。

def generateKey(keySize):
    # Creates public/private keys keySize bits in size.
    p = 0
    q = 0
    # Step 1: Create two prime numbers, p and q. Calculate n = p * q:
    print('Generating p prime...')
    while p == q:
        p = primeNum.generateLargePrime(keySize)
        q = primeNum.generateLargePrime(keySize)
    n = p * q

你在第 22 章的primeNum.py程序中写的generateLargePrime()函数在第 20 行和第 21 行返回两个质数作为整数值，我们将它们存储在变量p和q中。这是在一个while循环中完成的，只要p和q相同，该循环就会继续。如果generateLargePrime ()为p和q返回相同的整数，程序将再次尝试为p和q寻找唯一的质数。keySize中的值决定了p和q的大小。在第 22 行，我们将p和q相乘，并将乘积存储在n中。

接下来，在步骤 2 中，我们计算公钥的另一部分: e。

计算e值

通过找到一个与(p – 1) × (q – 1)互质的数来计算e的值。我们不会详细讨论为什么以这种方式计算e，但是我们希望e与(p – 1) × (q – 1)互质，因为这确保了e将总是产生唯一的密文。

使用一个无限的while循环，第 26 行计算一个数e，它与p – 1和q – 1的乘积互质。

    # Step 2: Create a number e that is relatively prime to (p-1)*(q-1):
    print('Generating e that is relatively prime to (p-1)*(q-1)...')
    while True:
        # Keep trying random numbers for e until one is valid:
        e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
        if cryptomath.gcd(e, (p - 1) * (q - 1)) == 1:
            break

第 28 行上的random.randrange()调用返回一个随机整数，并将其存储在e变量中。然后第 29 行使用cryptomath模块的gcd()函数测试e是否与(p - 1) * (q - 1)互质。如果e是互质的，那么第 30 行的break语句就跳出了无限循环。否则，程序执行跳回到第 26 行，继续尝试不同的随机数，直到找到一个与(p - 1) * (q - 1)互质的随机数。

接下来，我们计算私钥。

计算d值

第三步，找到用于解密的另一半私钥，也就是d。d只是e的模逆，我们已经在cryptomath模块中有了findModInverse()函数，我们在第 13 章中使用它来计算。

第 34 行调用findModInverse()并将结果存储在变量d中。

    # Step 3: Calculate d, the mod inverse of e:
    print('Calculating d that is mod inverse of e...')
    d = cryptomath.findModInverse(e, (p - 1) * (q - 1))

我们现在已经定义了生成公钥和私钥所需的所有数字。

找回密钥

回想一下，在公钥密码中，公钥和私钥各由两个数字组成。存储在n和e中的整数代表公钥，存储在n和d中的整数代表私钥。第 36 行和第 37 行将这些整数对作为元组值存储在publicKey和privateKey中。

    publicKey = (n, e)
    privateKey = (n, d)

在第 39 行和第 40 行使用print()调用，generateKey()函数中的其余行在屏幕上打印出密钥。

    print('Public key:', publicKey)
    print('Private key:', privateKey)

    return (publicKey, privateKey)

然后当调用generateKey()时，第 42 行返回一个包含publicKey和privateKey的元组。

在我们生成了公钥和私钥之后，我们还希望将它们存储在文件中，以便我们的公钥密码程序可以在以后使用它们来加密和解密。此外，将密钥存储在文件中非常有用，因为组成每个密钥的两个整数长达数百位，这使得它们难以记忆或方便地写下来。

使用makeKeyFiles()函数创建密钥文件

makeKeyFiles()函数通过将文件名和密钥大小作为参数将密钥存储在文件中。

def makeKeyFiles(name, keySize):
    # Creates two files 'x_pubkey.txt' and 'x_privkey.txt' (where x
    # is the value in name) with the n,e and d,e integers written in
    # them, delimited by a comma.

该函数创建格式为_pubkey.txt和_privkey.txt的两个文件，分别存储公钥和私钥。传递给函数的name参数决定了文件的部分。

为了防止再次运行程序时意外删除密钥文件，第 51 行检查具有给定名称的公钥或私钥文件是否已经存在。如果是这样，程序会退出并显示一条警告消息。

    # Our safety check will prevent us from overwriting our old key files:
    if os.path.exists('%s_pubkey.txt' % (name)) or
          os.path.exists('%s_privkey.txt' % (name)):
      sys.exit('WARNING: The file %s_pubkey.txt or %s_privkey.txt
            already exists! Use a different name or delete these files and
            rerun this program.' % (name, name))

在这个检查之后，第 54 行调用generateKey()并通过keySize来创建指定大小的公钥和私钥。

    publicKey, privateKey = generateKey(keySize)

generateKey()函数返回一个由两个元组组成的元组，它使用多重赋值将其赋给publicKey和privateKey变量。第一个元组有两个整数用于公钥，第二个元组有两个整数用于私钥。

现在我们已经完成了创建密钥文件的设置，我们可以创建实际的密钥文件了。我们将把组成每个密钥的两个数字存储在文本文件中。

第 56 行打印一个空行，然后第 57 行为用户打印关于公钥的信息。

    print()
    print('The public key is a %s and a %s digit number.' %
          (len(str(publicKey[0])), len(str(publicKey[1]))))
    print('Writing public key to file %s_pubkey.txt...' % (name))

第 57 行通过使用str()函数将这些值转换成字符串，然后使用len()函数找到字符串的长度，来指示在publicKey[0]和publicKey[1]的整数中有多少位数。然后，第 58 行报告公钥正被写入文件。

密钥文件的内容包括密钥大小、一个逗号、n整数、另一个逗号和e（或d）整数。例如，文件的内容应该是这样的:密钥大小，整数n,e或d，如下面的al_sweigart_pubkey.txt文件所示:

第 59 行到第 61 行以写模式打开_pubkey.txt文件，将密钥写入文件，然后关闭它。

    fo = open('%s_pubkey.txt' % (name), 'w')
    fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))
    fo.close()

第 63 到 68 行做的和第 56 到 61 行一样，除了它们把私钥写到_privatekey.txt文件中。

    print()
    print('The private key is a %s and a %s digit number.' %
          (len(str(publicKey[0])), len(str(publicKey[1]))))
    print('Writing private key to file %s_privkey.txt...' % (name))
    fo = open('%s_privkey.txt' % (name), 'w')
    fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
    fo.close()

确保没有人侵入你的电脑并复制这些密钥文件。如果他们获得了你的私人密钥文件，他们就能解密你所有的信息！

调用main()函数

在程序结束时，如果makePublicPrivateKeys.py作为一个程序运行，而不是作为一个模块被另一个程序导入，第 73 和 74 行调用main()函数。

# If makePublicPrivateKeys.py is run (instead of imported as a module),
# call the main() function:
if __name__ == '__main__':
    main()

现在你有了一个可以生成公钥和私钥的程序。虽然公钥密码在无法安全交换密钥的两个人之间开始通信时很有用，但由于公钥加密的缺点，它通常不用于所有加密通信。通常，公钥密码被用在混合密码系统中。

混合密码系统

RSA 和公钥加密需要大量的计算时间。对于每秒钟需要与其他计算机进行成千上万次加密连接的服务器来说尤其如此。作为一种变通方法，人们可以使用公钥加密来加密和分发密钥，以获得更快的对称密钥密码，这是解密和加密密钥相同的任何类型的密码。在使用公钥加密的消息将对称密码的密钥安全地发送给接收方之后，发送方可以将对称密码用于将来的消息。使用对称密钥密码和非对称密钥密码进行通信被称为混合密码系统。你可以在en.wikipedia.org/wiki/Hybrid_cryptosystem了解更多关于混合密码系统的信息。

总结

在本章中，您学习了公钥加密的工作原理，以及如何编写生成公钥和私钥的程序。在第 24 章中，你将使用这些密钥来执行使用公钥密码的加密和解密。

练习题

练习题的答案可以在本书的网站www.nostarch.com/crackingcodes找到。

1. 对称密码和非对称密码有什么区别？

2. Alice 生成一个公钥和一个私钥。不幸的是，她后来丢失了她的私钥。

   1. 其他人能给她发送加密信息吗？

   2. 她能够解密之前发给她的信息吗？

   3. 她能够对文档进行数字签名吗？

   4. 其他人能够验证她之前签署的文件吗？

3. 什么是认证和保密？它们有什么不同？

4. 什么是不可否认性？

二十四、公钥密码的编程

原文：https://inventwithpython.com/cracking/chapter24.html

“一位同事曾经告诉我，这个世界充满了糟糕的安全系统，它们是由阅读应用密码学的人设计的。”

——布鲁斯·施奈尔，《应用密码学》的作者

在第 23 章中，您学习了公钥加密的工作原理，以及如何使用公钥生成程序生成公钥和私钥文件。现在，您已经准备好将您的公钥文件发送给其他人（或在线发布），这样他们就可以

在发送给你之前用它来加密他们的信息。在本章中，您将编写公钥密码程序，该程序使用您生成的公钥和私钥对消息进行加密和解密。

警告

本书中公钥密码的实现基于 RSA 密码。然而，我们在这里没有涉及的许多其他细节使得这个密码不适合在现实世界中使用。虽然公钥密码不受本书中密码分析技术的影响，但它容易受到专业密码学家今天使用的高级技术的攻击。

本章涵盖的主题

• pow()函数

• min()和max()函数

• insert()列表方法

公钥密码的工作原理

与我们以前编写的密码类似，公钥密码将字符转换成数字，然后对这些数字进行数学运算来加密它们。公钥密码与您所了解的其他密码的不同之处在于，它将多个字符转换成一个称为块的整数，然后一次加密一个块。

公钥密码需要在表示多个字符的块上工作的原因是，如果我们对单个字符使用公钥加密算法，相同的明文字符将总是加密成相同的密文字符。因此，公钥密码与简单的数学替换密码没有什么不同。

创建块

在密码学中，块是一个大整数，代表固定数量的文本字符。我们将在本章中创建的publicKeyCipher.py程序将消息字符串值转换成块，每个块是一个表示 169 个文本字符的整数。最大块大小取决于符号集大小和密钥大小。在我们的程序中，符号集是 66 个字符串'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz1234567890 !?.'，它包含了一个消息可以拥有的唯一字符。

等式2 ** keySize > len(SYMBOLS) ** blockSize必须为真。例如，当您使用 1024 位密钥和 66 个字符的符号集时，最大块大小是一个最多 169 个字符的整数，因为2 ** 1024大于66 * 169。但是2 ** 1024不大于66 * 170。如果你使用太大的块，公钥密码的数学将不起作用，你将不能解密程序产生的密文。

让我们探索一下如何将一个消息字符串转换成一个大的整数块。

将字符串转换成块

正如在我们以前的密码程序中一样，我们可以使用符号集字符串的索引将文本字符转换为整数，反之亦然。我们将符号集存储在名为SYMBOLS的常量中，其中索引0处的字符是'A'，索引1处的字符是'B'，以此类推。在交互式 shell 中输入以下内容，查看这种转换是如何进行的:

>>> SYMBOLS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz123456
7890 !?.'
>>> len(SYMBOLS)
66
>>> SYMBOLS[0]
'A'
>>> SYMBOLS[30]
'e'

我们可以通过符号集中的整数索引来表示文本字符。但是，我们还需要一种方法，将这些小整数组合成一个代表一个块的大整数。

为了创建块，我们将字符的符号集索引乘以符号集大小的递增幂。这个区块是所有这些数字的总和。让我们看一个例子，使用下面的步骤将小整数组合成一个大的字符串块'Howdy'。

该块的整数从0开始，符号集的长度为 66 个字符。以这些数字为例，在交互式 shell 中输入以下内容:

>>> blockInteger = 0
>>> len(SYMBOLS)
66

'Howdy'消息中的第一个字符是'H'，因此我们找到该字符的符号集索引，如下所示:

>>> SYMBOLS.index('H')
7

因为这是消息的第一个字符，所以我们将它的符号集索引乘以66 ** 0（在 Python 中，指数运算符是**），计算结果为7。我们将该值添加到块中:

>>> 7 * (66 ** 0)
7
>>> blockInteger = blockInteger + 7

然后我们为'Howdy'中的第二个字符'o'找到符号集索引。因为这是消息的第二个字符，我们将'o'的符号集索引乘以66 ** 1而不是66 ** 0，然后将其添加到块中:

>>> SYMBOLS.index('o')
40
>>> blockInteger += 40 * (66 ** 1)
>>> blockInteger
2647

该块现在是2647。我们可以使用一行代码来缩短查找每个字符的符号集索引的过程:

>>> blockInteger += SYMBOLS.index('w') * (len(SYMBOLS) ** 2)
>>> blockInteger += SYMBOLS.index('d') * (len(SYMBOLS) ** 3)
>>> blockInteger += SYMBOLS.index('y') * (len(SYMBOLS) ** 4)
>>> blockInteger
957285919

将'Howdy'编码到一个大整数块中会产生整数 957，285，919，它唯一地引用该字符串。通过继续使用越来越大的 66 次方，我们可以使用一个大整数来表示最大到块大小的任意长度的字符串。例如，277，981 是表示字符串'42!'的块，10，627，106，169，278，065，987，481，042，235，655，809，080，528 表示字符串'I named my cat Zophie.'。

因为我们的块大小是 169，所以我们在单个块中最多只能加密 169 个字符。如果我们要编码的消息超过 169 个字符，我们可以使用更多的块。在publicKeyCipher.py程序中，我们将使用逗号来分隔各个块，以便用户可以识别一个块何时结束，下一个块何时开始。

表 24-1 包含了一个分成块的示例消息，并显示了代表每个块的整数。每个块最多可以存储 169 个字符的消息。

表 24-1： 一条消息拆分成块

第一块 -> （169 个字符）

Alan Mathison Turing was a British cryptanalyst and computer scientist. He was highly influential in the development of computer science and provided a formalisation of

3013810338120027658120611166332270159047154
7608326152595431391575797140707837485089852
659286061395648657712401264848061468979996
871106525448961558640277994456848107158423
162065952633246425985956987627719631460939
2565956887693059829154012923414594664511373
093526087354321666137736234609864038110994
85392482698

第二块 -> （169 个字符）

the concepts of algorithm and computation with the Turing machine. Turing is widely considered to be the father of computer science and artificial intelligence. During W

1106890780922147455215935080195634373132680
102708192713651484085475402677752791958075
872272026708702634070281109709555761008584
1376819190225258032442691476944762174257333
902148064107269871669093655004577014280290
4244524711751435049117398986044838791597315
078937194860112574798016587564452792451567
15863348631

第三块 -> （82 个字符）

orld War II he worked for the Government Code and Cypher School at Bletchley Park.

1583679754961601914428952447217583697875837
635974864128047509439056559022732095918077
290541944859809053286915764228326887495095
27709935741799076979034

|

在本例中，420 个字符的消息由两个 169 个字符的块组成，需要第三个块来容纳剩余的 82 个字符。

公钥密码加密与解密的数学

现在您已经知道了如何将字符转换成块整数，让我们来探索公钥密码如何使用数学来加密每个块。

以下是公钥密码的一般公式:

C = M^e mod n
M = C^d mod n

我们用第一个等式加密每个整数块，用第二个等式解密。M表示消息分组整数，C为密文分组整数。数字e和n组成加密的公钥，数字d和n组成私钥。回想一下，每个人，包括密码分析者，都可以访问公钥(e, n)。

通常，我们通过将每个块的整数提升到e的幂来创建加密的消息，就像我们在上一节中计算的那样，并通过n来修改结果。该计算产生一个整数，表示加密块C。组合所有的块产生完整的加密消息。

比如我们把五个字符的字符串'Howdy'加密后发给爱丽丝。当转换为整数块时，消息为[957285919]（完整的消息适合一个块，所以列表值中只有一个整数）。Alice 的公钥是 64 位，太小了，不安全，但是我们将使用它来简化本例中的输出。其n为 116284564958604315258674918142848831759，e为 13805220545651593223。（对于 1024 位密钥，这些数字会大得多。）

要加密，我们通过将这些数字传递给 Python 的pow()函数，计算(957285919 ** 13805220545651593223) % 116284564958604315258674918142848831759，就像这样:

>>> pow(957285919, 13805220545651593223, 
      116284564958604315258674918142848831759)
43924807641574602969334176505118775186

Python 的pow()函数使用了一种叫做模幂运算的数学技巧来快速计算如此大的指数。事实上，对表达式(957285919 ** 13805220545651593223) % 116284564958604315258674918142848831759求值会得到相同的答案，但需要几个小时才能完成。pow()返回的整数是一个表示加密消息的块。

要解密，加密消息的接收者需要有私钥(d, n)，将每个加密块的整数提升到d的幂，然后用n进行取模。当所有解密的块被解码成字符并组合时，接收者将得到原始的明文消息。

例如，Alice 尝试解密块整数 43，924，807，641，574，602，969，334，176，505，118，775，186。她的私钥的n与她的公钥的n相同，但是她的私钥的d为 7242447594969014539697070764378340583。为了解密，她运行以下代码:

>>> pow(43924807641574602969334176505118775186, 
      72424475949690145396970707764378340583, 
      116284564958604315258674918142848831759)
957285919

当我们将块整数957285919转换成一个字符串时，我们得到了'Howdy'，这是原始消息。接下来，您将学习如何将块转换为字符串。

将块转换成字符串

要将块解密为原始的块整数，第一步是将其转换为每个文本字符的小整数。这个过程从添加到块中的最后一个字符开始。我们使用底除法和模运算符来计算每个文本字符的小整数。

回想一下，上一个'Howdy'示例中的块整数是957285919；原始消息有五个字符长，使得最后一个字符的索引为 4；并且用于该消息的符号集是 66 个字符长。为了确定最后一个字符的符号集索引，我们计算957,285,919 / 66 ** 4 并向下舍入，得到 50。我们可以使用整数除法运算符（//）进行除法和向下舍入。符号集（SYMBOLS[50]）中索引 50 处的字符是'y'，这实际上是'Howdy'消息的最后一个字符。

在交互式 shell 中，我们使用以下代码计算这个块整数:

>>> blockInteger = 957285919
>>> SYMBOLS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz123456
7890 !?.'
>>> blockInteger // (66 ** 4)
50
>>> SYMBOLS[50]
'y'

下一步是将块整数乘以66 ** 4以获得下一个块整数。计算957,285,919 % (66 ** 4)得到 8,549,119，这恰好是字符串'Howd'的块整数值。我们可以用66 ** 3的底除法来确定这个方块的最后一个字符。为此，请在交互式 shell 中输入以下内容:

>>> blockInteger = 8549119
>>> SYMBOLS[blockInteger // (len(SYMBOLS) ** 3)]
'd'

这个块的最后一个字符是'd'，使得转换后的字符串到目前为止'dy'。我们可以像以前一样从块整数中删除这个字符:

>>> blockInteger = blockInteger % (len(SYMBOLS) ** 3)
>>> blockInteger
211735

整数211735是字符串'How'的块。通过继续这个过程，我们可以从块中恢复完整的字符串，就像这样:

>>> SYMBOLS[blockInteger // (len(SYMBOLS) ** 2)]
'w'
>>> blockInteger = blockInteger % (len(SYMBOLS) ** 2)
>>> SYMBOLS[blockInteger // (len(SYMBOLS) ** 1)]
'o'
>>> blockInteger = blockInteger % (len(SYMBOLS) ** 1)
>>> SYMBOLS[blockInteger // (len(SYMBOLS) ** 0)]
'H'

现在您知道了如何从原始块整数值957285919中检索字符串'Howdy'中的字符。

为什么我们无法破解公钥密码

当公钥密码正确实现时，我们在本书中使用的所有不同类型的加密攻击对公钥密码都是无用的。以下是几个原因:

1. 暴力攻击不会起作用，因为有太多可能的密钥需要检查。

2. 字典攻击不会起作用，因为密钥基于数字，而不是单词。

3. 单词模式攻击不起作用，因为相同的明文单词可以根据它在块中出现的位置进行不同的加密。

4. 频率分析不起作用，因为单个加密块代表几个字符；我们无法获得单个字符的频率计数。

因为公钥(e, n)是大家都知道的，如果密码分析者能够截获密文，他们就会知道e，n，和C。但是在不知道d的情况下，数学上不可能解出原始消息M。

回想一下第 23 章中的e与数字(p – 1) × (q – 1)互质，并且d是e和(p – 1) × (q – 1)的模逆。在第十三章中，你了解到两个数的模逆是通过对方程(ai) % m = 1 求i来计算的，其中a和m是模问题a mod m中的两个数。这意味着密码分析者知道d是e mod (p – 1) × (q – 1)的逆，所以我们可以通过求解方程ed mod (p – 1) × (q – 1)找到d得到整个解密密钥.但是，没有办法知道什么是(p – 1) × (q – 1)。

我们从公钥文件中知道密钥的大小，所以密码分析者知道p和q小于2 ** 1024并且e与(p – 1) × (q – 1)互质。但是e和很多的数字是相对质数，在 0 到2 ** 1024的范围内寻找(p – 1) × (q – 1)可能的数字对暴力来说是一个太大的问题。

虽然这还不足以破解密码，但密码分析员可以从公开密钥中收集到另一个线索。公钥由两个数字组成（ e、n，我们知道n = p × q，因为这是我们在第 23 章中创建公钥和私钥时计算n的方法。而且因为p和q都是质数，所以对于一个给定的数n，可以正好有两个数可以是p和q。

回想一下，一个质数除了 1 和它本身之外，没有任何因子。因此，如果你把两个质数相乘，乘积将只有 1 和它自己以及你开始时的两个质数作为它的因数。

因此，要破解公钥密码，我们需要做的就是找出n的因子。因为我们知道两个且只有两个数可以相乘得到n，所以我们不会有太多不同的数可供选择。在我们算出哪两个质数（ p和q相乘得到n之后，我们就可以计算(p – 1) × (q – 1)，然后用那个结果来计算d。这个计算似乎很容易做到。让我们用我们在第 22 章的primeNum.py程序中写的isPrime()函数来做计算。

我们可以修改isPrime()来返回它找到的第一个因子，因为我们知道除了 1 和n之外，只能有两个因子n :

def isPrime(num):
    # Returns (p,q) where p and q are factors of num.
    # See if num is divisible by any number up to the square root of num:
    for i in range(2, int(math.sqrt(num)) + 1):
        if num % i == 0:
            return (i, num / i)
    return None # No factors exist for num; num must be prime.

如果我们编写一个公钥密码破解程序，我们可以只调用这个函数，将n传递给它（我们将从公钥文件中获得），并等待它找到因子p和q。然后我们可以找到(p – 1) × (q – 1)是什么，这意味着我们可以计算e mod (p – 1) × (q – 1)的模逆，以获得d，即解密密钥。那么计算明文消息M就容易了。

但是有一个问题。回想一下，n是一个大约 600 位数的数字。Python 的math.sqrt()函数不能处理这么大的数字，所以它会给你一个错误消息。但是，即使它能够处理这个数字，Python 也要执行那个for循环很长时间。以为例，即使你的计算机从现在开始继续运行 50 亿年，它仍然几乎没有机会找到n的因子。这些数字就是这么大。

而这正是公钥密码的长处:数学上，求一个数的因子没有捷径。很容易得出两个质数p和q，将它们相乘得到n。但是，几乎不可能得到一个数字n并计算出p和q会是多少。例如，当你看到像 15 这样的小数字时，你可以很容易地说 5 和 3 是两个相乘等于 15 的数字。但要想搞清楚一个数字的因子，比如 178,565,887,643,607,245,654,502,737，完全是另一回事。这个事实使得公钥密码实际上不可能被破解。

公钥密码程序的源代码

选择文件 -> 新文件，打开新文件编辑器窗口。在文件编辑器中输入以下代码，保存为publicKeyCipher.py。

publicKey
Cipher.py

# Public Key Cipher
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)

import sys, math

# The public and private keys for this program are created by
# the makePublicPrivateKeys.py program.
# This program must be run in the same folder as the key files.

SYMBOLS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz12345
       67890 !?.'

def main():
    # Runs a test that encrypts a message to a file or decrypts a message
    # from a file.
    filename = 'encrypted_file.txt' # The file to write to/read from.
    mode = 'encrypt' # Set to either 'encrypt' or 'decrypt'.

    if mode == 'encrypt':
        message = 'Journalists belong in the gutter because that is where
               the ruling classes throw their guilty secrets. Gerald Priestland.
               The Founding Fathers gave the free press the protection it must
               have to bare the secrets of government and inform the people.
               Hugo Black.'
        pubKeyFilename = 'al_sweigart_pubkey.txt'
        print('Encrypting and writing to %s...' % (filename))
        encryptedText = encryptAndWriteToFile(filename, pubKeyFilename,
               message)

        print('Encrypted text:')
        print(encryptedText)

    elif mode == 'decrypt':
        privKeyFilename = 'al_sweigart_privkey.txt'
        print('Reading from %s and decrypting...' % (filename))
        decryptedText = readFromFileAndDecrypt(filename, privKeyFilename)

        print('Decrypted text:')
        print(decryptedText)


def getBlocksFromText(message, blockSize):
    # Converts a string message to a list of block integers.
    for character in message:
        if character not in SYMBOLS:
            print('ERROR: The symbol set does not have the character %s' %
                   (character))
            sys.exit()
    blockInts = []
    for blockStart in range(0, len(message), blockSize):
        # Calculate the block integer for this block of text:
        blockInt = 0
        for i in range(blockStart, min(blockStart + blockSize,
               len(message))):
            blockInt += (SYMBOLS.index(message[i])) * (len(SYMBOLS) **
                   (i % blockSize))
        blockInts.append(blockInt)
    return blockInts


def getTextFromBlocks(blockInts, messageLength, blockSize):
    # Converts a list of block integers to the original message string.
    # The original message length is needed to properly convert the last
    # block integer.
    message = []
    for blockInt in blockInts:
        blockMessage = []
        for i in range(blockSize - 1, -1, -1):
            if len(message) + i < messageLength:
                # Decode the message string for the 128 (or whatever
                # blockSize is set to) characters from this block integer:
                charIndex = blockInt // (len(SYMBOLS) ** i)
                blockInt = blockInt % (len(SYMBOLS) ** i)
                blockMessage.insert(0, SYMBOLS[charIndex])
        message.extend(blockMessage)
    return ''.join(message)


def encryptMessage(message, key, blockSize):
    # Converts the message string into a list of block integers, and then
    # encrypts each block integer. Pass the PUBLIC key to encrypt.
    encryptedBlocks = []
    n, e = key

    for block in getBlocksFromText(message, blockSize):
        # ciphertext = plaintext ^ e mod n
        encryptedBlocks.append(pow(block, e, n))
    return encryptedBlocks


def decryptMessage(encryptedBlocks, messageLength, key, blockSize):
    # Decrypts a list of encrypted block ints into the original message
    # string. The original message length is required to properly decrypt
    # the last block. Be sure to pass the PRIVATE key to decrypt.
    decryptedBlocks = []
    n, d = key
    for block in encryptedBlocks:
        # plaintext = ciphertext ^ d mod n
        decryptedBlocks.append(pow(block, d, n))
    return getTextFromBlocks(decryptedBlocks, messageLength, blockSize)


def readKeyFile(keyFilename):
    # Given the filename of a file that contains a public or private key,
    # return the key as a (n,e) or (n,d) tuple value.
    fo = open(keyFilename)
    content = fo.read()
    fo.close()
    keySize, n, EorD = content.split(',')
    return (int(keySize), int(n), int(EorD))


def encryptAndWriteToFile(messageFilename, keyFilename, message,
       blockSize=None):
    # Using a key from a key file, encrypt the message and save it to a
    # file. Returns the encrypted message string.
    keySize, n, e = readKeyFile(keyFilename)
    if blockSize == None:
        # If blockSize isn't given, set it to the largest size allowed by
               the key size and symbol set size.
        blockSize = int(math.log(2 ** keySize, len(SYMBOLS)))
    # Check that key size is large enough for the block size:
    if not (math.log(2 ** keySize, len(SYMBOLS)) >= blockSize):
        sys.exit('ERROR: Block size is too large for the key and symbol
               set size. Did you specify the correct key file and encrypted
               file?')
    # Encrypt the message:
    encryptedBlocks = encryptMessage(message, (n, e), blockSize)

    # Convert the large int values to one string value:
    for i in range(len(encryptedBlocks)):
        encryptedBlocks[i] = str(encryptedBlocks[i])
    encryptedContent = ','.join(encryptedBlocks)

    # Write out the encrypted string to the output file:
    encryptedContent = '%s_%s_%s' % (len(message), blockSize,
           encryptedContent)
    fo = open(messageFilename, 'w')
    fo.write(encryptedContent)
    fo.close()
    # Also return the encrypted string:
    return encryptedContent


def readFromFileAndDecrypt(messageFilename, keyFilename):
    # Using a key from a key file, read an encrypted message from a file
    # and then decrypt it. Returns the decrypted message string.
    keySize, n, d = readKeyFile(keyFilename)


    # Read in the message length and the encrypted message from the file:
    fo = open(messageFilename)
    content = fo.read()
    messageLength, blockSize, encryptedMessage = content.split('_')
    messageLength = int(messageLength)
    blockSize = int(blockSize)

    # Check that key size is large enough for the block size:
    if not (math.log(2 ** keySize, len(SYMBOLS)) >= blockSize):
        sys.exit('ERROR: Block size is too large for the key and symbol
               set size. Did you specify the correct key file and encrypted
               file?')

    # Convert the encrypted message into large int values:
    encryptedBlocks = []
    for block in encryptedMessage.split(','):
        encryptedBlocks.append(int(block))

    # Decrypt the large int values:
    return decryptMessage(encryptedBlocks, messageLength, (n, d),
           blockSize)


# If publicKeyCipher.py is run (instead of imported as a module), call
# the main() function.
if __name__ == '__main__':
    main()

公钥密码程序的运行示例

让我们试着运行publicKeyCipher.py程序来加密一条秘密消息。要向使用此程序的人发送秘密消息，请获取此人的公钥文件，并将其放在与程序文件相同的目录中。

要加密消息，确保第 16 行的mode变量被设置为字符串'encrypt'。将第 19 行的message变量更新为您想要加密的消息字符串。然后将第 20 行的pubKeyFilename变量设置为公钥文件的文件名。第 21 行的filename变量保存了密文被写入的文件名。filename、pubKeyFilename和message变量都被传递给encryptAndWriteToFile()以加密消息并将其保存到文件中。

运行程序时，输出应该是这样的:

Encrypting and writing to encrypted_file.txt...
Encrypted text:
258_169_45108451524907138236859816039483721219475907590237903918239237768643699
4856660301323157253724978022861702098324427738284225530186213380188880577329634
8339229890890464969556937797072434314916522839692277034579463594713843559898418
9307234650088689850744361262707129971782407610450208047927129687841621734776965
7018277918490297215785759257290855812221088907016904983025542174471606494779673
6015310089155876234277883381345247353680624585629672939709557016107275469388284
5124192568409483737233497304087969624043516158221689454148096020738754656357140
74772465708958607695479122809498585662785064751254235489968738346795649,1253384
3336975115539761332250402699868835150623017582438116840049236083573741817645933
3719456453133658476271176035248597021972316454526545069452838766387599839340542
4066877721135511313454252589733971962219016066614978390378611175964456773669860
9429545605901714339082542725015140530985685117232598778176545638141403657010435
3859244660091910391099621028192177415196156469972977305212676293746827002983231
4668240693230032141097312556400629961518635799478652196072316424918648787555631
6339424948975804660923616682767242948296301678312041828934473786824809308122356
133539825048880814063389057192492939651199537310635280371

程序将这个输出写到一个名为encrypted_file.txt的文件中。这是对第 19 行的message变量中的字符串的加密。因为您使用的公钥可能与我的不同，所以您得到的输出可能不同，但是输出的格式应该是相同的。正如您在本例中所看到的，加密分为两个块，或两个大整数，用逗号分隔。

加密开始处的数字258代表原始消息长度，后面是下划线和另一个数字169，代表块大小。要解密此消息，将mode变量改为'decrypt'，并再次运行程序。与加密一样，确保第 28 行的privKeyFilename被设置为私钥文件名，并且该文件与publicKeyCipher.py在同一个文件夹中。此外，确保加密文件encrypted_file.txt与publicKeyCipher.py在同一个文件夹中。当您运行程序时，encrypted_file.txt中的加密消息被解密，输出应该是这样的:

Reading from encrypted_file.txt and decrypting...
Decrypted text:
Journalists belong in the gutter because that is where the ruling classes throw
their guilty secrets. Gerald Priestland. The Founding Fathers gave the free
press the protection it must have to bare the secrets of government and inform
the people. Hugo Black.

注意publicKeyCipher.py程序只能加密和解密普通（简单）文本文件。

让我们仔细看看publicKeyCipher.py程序的源代码。

设置程序

公钥密码处理数字，所以我们将把字符串消息转换成整数。这个整数是基于符号集中的索引计算的，存储在第 10 行的SYMBOLS变量中。

# Public Key Cipher
# https://www.nostarch.com/crackingcodes/ (BSD Licensed)

import sys, math

# The public and private keys for this program are created by
# the makePublicPrivateKeys.py program.
# This program must be run in the same folder as the key files.

SYMBOLS = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz12345
       67890 !?.'

程序如何确定是加密还是解密

通过将值存储在变量中，publicKeyCipher.py程序决定是否加密或解密文件，以及使用哪个密钥文件。在我们研究这些变量如何工作的同时，我们还将研究程序如何打印加密和解密输出。

我们告诉程序它应该在main()内加密还是解密:

def main():
    # Runs a test that encrypts a message to a file or decrypts a message
    # from a file.
    filename = 'encrypted_file.txt' # The file to write to/read from.
    mode = 'encrypt' # Set to either 'encrypt' or 'decrypt'.

如果第 16 行的mode设置为'encrypt'，程序通过将信息写入filename中指定的文件来加密信息。如果mode设置为'decrypt'，程序读取加密文件的内容（由filename指定）进行解密。

第 18 到 25 行指定了如果程序确认用户想要加密文件，它应该做什么。

    if mode == 'encrypt':
        message = 'Journalists belong in the gutter because that is where
               the ruling classes throw their guilty secrets. Gerald Priestland.
               The Founding Fathers gave the free press the protection it must
               have to bare the secrets of government and inform the people.
               Hugo Black.'
        pubKeyFilename = 'al_sweigart_pubkey.txt'
        print('Encrypting and writing to %s...' % (filename))
        encryptedText = encryptAndWriteToFile(filename, pubKeyFilename,
               message)

        print('Encrypted text:')
        print(encryptedText)

第 19 行的message变量包含要加密的文本，第 20 行的pubKeyFilename包含公钥文件的文件名，在本例中为al_sweigart_pubkey.txt。请记住，该消息只能包含SYMBOLS变量中的字符，这是该密码的符号集。第 22 行调用encryptAndWriteToFile()函数，该函数使用公钥加密message，并将加密的消息写入filename指定的文件。

第 27 到 28 行告诉程序如果mode被设置为'decrypt'该做什么。程序从第 28 行的privKeyFilename中的私有密钥文件中读取，而不是加密。

    elif mode == 'decrypt':
        privKeyFilename = 'al_sweigart_privkey.txt'
        print('Reading from %s and decrypting...' % (filename))
        decryptedText = readFromFileAndDecrypt(filename, privKeyFilename)

        print('Decrypted text:')
        print(decryptedText)

然后我们将filename和privKeyFilename变量传递给readFromFileAndDecrypt ()函数（稍后在程序中定义），该函数返回解密的消息。第 30 行将来自readFromFileAndDecryptT5 的返回值存储在decryptedText中，第 33 行将其打印到屏幕上。这是main()函数的结尾。

现在让我们看看如何执行公钥密码的其他步骤，例如将消息转换成块。

使用getBlocksFromText()将字符串转换为块

让我们看看程序如何将消息字符串转换成 128 字节的块。第 36 行上的getBlocksFromText()函数将一个message和一个块大小作为参数，返回一个表示消息的块列表或一个大整数值列表。

def getBlocksFromText(message, blockSize):
    # Converts a string message to a list of block integers.
    for character in message:
        if character not in SYMBOLS:
            print('ERROR: The symbol set does not have the character %s' %
                   (character))
            sys.exit()

第 38 到 41 行确保消息参数只包含在SYMBOLS变量的符号集中的文本字符。blockSize参数是可选的，可以采用任何块大小。为了创建块，我们首先将字符串转换成字节。

为了生成一个块，我们将所有的符号集索引组合成一个大整数，正如我们在第 350 页的“将字符串转换成块”中所做的那样。当我们创建块时，我们将使用第 42 行的blockInts空列表来存储它们。

    blockInts = []

我们希望块的长度为blockSize字节，但是当消息不能被blockSize整除时，最后一个块的长度将小于blockSize字符。为了处理这种情况，我们使用了min()函数。

min()和max()函数

min()函数返回其参数的最小值。在交互式 shell 中输入以下内容，看看min()函数是如何工作的:

>>> min(13, 32, 13, 15, 17, 39)
13

您还可以将单个列表或元组值作为参数传递给min()。在交互式 shell 中输入以下内容以查看示例:

>>> min([31, 26, 20, 13, 12, 36])
12
>>> spam = (10, 37, 37, 43, 3)
>>> min(spam)
3

在这种情况下，min(spam)返回列表或元组中的最小值。与min()相反的是max()，它返回其参数的最大值，如下所示:

>>> max(18, 15, 22, 30, 31, 34)
34

让我们回到我们的代码，看看publicKeyCipher.py程序如何使用min()来确保message的最后一个块被截断到合适的大小。

在blockInt中存储块

第 43 行的for循环中的代码通过将blockStart中的值设置为正在创建的块的索引来为每个块创建整数。

    for blockStart in range(0, len(message), blockSize):
        # Calculate the block integer for this block of text:
        blockInt = 0
        for i in range(blockStart, min(blockStart + blockSize,
               len(message))):

我们将存储我们在blockInt中创建的块，我们最初在第 45 行将其设置为0。第 46 行的for循环将i设置为来自message的块中所有字符的索引。这些索引应该从blockStart开始，上升到blockStart + blockSize或len(message)，以较小者为准。第 46 行的min()调用返回这两个表达式中较小的一个。

第 46 行的range()的第二个参数应该是blockStart + blockSize和len(message)中较小的一个，因为除了最后一个块的之外，每个块总是由 128 个字符*（或者blockSize中的任何值）组成。最后一个块可能正好是 128 个字符，但更有可能少于全部 128 个字符。在这种情况下，我们希望i在len(message)停止，因为这是message中的最后一个索引。

有了组成块的字符后，我们使用数学将字符转换成一个大整数。回想一下在第 350 页的“将字符串转换成块中，我们通过将每个字符的符号集索引整数值乘以66 ** SYMBOLS.index(66 是SYMBOLS字符串的长度）创建了一个大整数。为了在代码中做到这一点，我们为每个字符计算SYMBOLS.index(message[i])（字符的符号集索引整数值）乘以(len(SYMBOLS) ** (i % blockSize))，并将每个结果加到blockInt。

            blockInt += (SYMBOLS.index(message[i])) * (len(SYMBOLS) **
                   (i % blockSize))

我们希望指数是相对于当前迭代的块的索引，它总是从0到blockSize。我们不能直接使用变量i作为等式的字符索引部分，因为它指的是整个message字符串中的索引，从0到len(message)都有索引。使用i会产生一个比 66 大得多的整数。通过用blockSize修改i，我们可以得到相对于块的索引，这就是为什么第 47 行是len(SYMBOLS) ** (i % blockSize)而不是简单的len(SYMBOLS) ** i。

在第 46 行上的for循环完成后，已经计算了该块的整数。我们使用第 48 行的代码将这个块整数附加到blockInts列表中。第 43 行的for循环的下一次迭代计算消息的下一个块的块整数。

        blockInts.append(blockInt)
    return blockInts

在第 43 行的for循环结束后，所有的块整数应该已经被计算并存储在blockInts列表中。49 线从getBlocksFromText()返回blockInts。

此时，我们已经将整个message字符串转换成了块整数，但是我们还需要一种方法来将块整数转换回原始的明文消息，以用于解密过程，这是我们接下来要做的。

使用getTextFromBlocks()解密

第 52 行的getTextFromBlocks()函数与getBlocksFromText ()函数相反。这个函数将一列块整数作为参数blockInts、消息的长度和blockSize来返回这些块代表的字符串值。我们需要messageLength中编码消息的长度，因为getTextFromBlocks()函数使用这个信息从最后一个块整数中获取字符串，当它的大小不是blockSize字符时。该过程在第 354 页的将块转换成字符串中有所描述。

def getTextFromBlocks(blockInts, messageLength, blockSize):
    # Converts a list of block integers to the original message string.
    # The original message length is needed to properly convert the last
    # block integer.
    message = []

第 56 行创建的空白列表message为每个字符存储了一个字符串值，我们将从blockInts中的块整数中计算这个值。

第 57 行的for循环遍历blockInts列表中的每个块整数。在for循环中，第 58 到 65 行的代码计算当前迭代块中的字母。

    for blockInt in blockInts:
        blockMessage = []
        for i in range(blockSize - 1, -1, -1):

getTextFromBlocks()中的代码将每个块整数分割成blockSize个整数，每个整数代表一个字符的符号集索引。我们必须反向工作以从blockInt中提取符号集索引，因为当我们加密消息时，我们从较小的指数（66 ** 0，66 ** 1，66 ** 2等等）开始，但是当解密时，我们必须首先使用较大的指数进行除法和模运算。这就是为什么第 59 行上的for循环从blockSize - 1开始，然后在每次迭代中减去1，直到（但不包括）-1。这意味着最后一次迭代中i的值是0。

在我们将符号集索引转换为字符之前，我们需要确保解码的块没有超过message的长度。为此，我们检查到目前为止已经从块中翻译出来的字符数len(message) + i，仍然少于第 60 行的messageLength。

            if len(message) + i < messageLength:
                # Decode the message string for the 128 (or whatever
                # blockSize is set to) characters from this block integer.
                charIndex = blockInt // (len(SYMBOLS) ** i)
                blockInt = blockInt % (len(SYMBOLS) ** i)

为了从块中获取字符，我们遵循第 354 页上的“将块转换成字符串中描述的过程。我们将每个字符放入到message列表。对每个块进行编码实际上颠倒了字符，这一点你早就看到了，所以我们不能只把解码后的字符附加到message上。相反，我们在message的前面插入字符，这需要用insert()列表方法来完成。

使用insert()列表方法

append()列表方法只在列表末尾添加值，但是insert()列表方法可以在列表的任意位置添加值。insert()方法将列表中要插入值的位置的整数索引和要插入的值作为其参数。在交互式 shell 中输入以下内容，看看insert()方法是如何工作的:

>>> spam = [2, 4, 6, 8]
>>> spam.insert(0, 'hello')
>>> spam
['hello', 2, 4, 6, 8]
>>> spam.insert(2, 'world')
>>> spam
['hello', 2, 'world', 4, 6, 8]

在这个例子中，我们创建一个spam列表，然后在0索引处插入字符串'hello'。如您所见，我们可以在列表中的任何现有索引处插入值，比如在索引2处。

将消息列表合并成字符串

我们可以使用SYMBOLS字符串将charIndex中的符号集索引转换为相应的字符，并将该字符插入到列表开头的索引0处。

                blockMessage.insert(0, SYMBOLS[charIndex])
        message.extend(blockMessage)
    return ''.join(message)

然后这个字符串从getTextFromBlocks()返回。

编写encryptMessage()函数

encryptMessage()函数使用message中的明文字符串和存储在key中的公钥的两个整数元组对每个块进行加密，这是用我们将在本章后面编写的readKeyFile()函数创建的。encryptMessage()函数返回加密块的列表。

def encryptMessage(message, key, blockSize):
    # Converts the message string into a list of block integers, and then
    # encrypts each block integer. Pass the PUBLIC key to encrypt.
    encryptedBlocks = []
    n, e = key

第 73 行创建了encryptedBlocks变量，它以一个空列表开始，该列表将保存整数块。然后第 74 行将key中的两个整数分配给变量n和e。现在我们已经设置了公钥变量，我们可以对每个要加密的消息块执行数学运算。

为了加密每个块，我们对它执行一些数学运算，得到一个新的整数，这就是加密的块。我们将模块提升到e的幂，然后使用第 78 行的pow(block, e, n)通过n对其进行修改。

    for block in getBlocksFromText(message, blockSize):
        # ciphertext = plaintext ^ e mod n
        encryptedBlocks.append(pow(block, e, n))
    return encryptedBlocks

加密的块整数然后被附加到encryptedBlocks。

编写decryptMessage()函数

第 82 行的decryptMessage()函数解密块并返回解密的消息字符串。它将加密块列表、消息长度、私钥和块大小作为参数。

我们在第 86 行设置的decryptedBlocks变量存储了解密块的列表，并使用多重赋值技巧，将key元组的两个整数分别放在n和d中。

def decryptMessage(encryptedBlocks, messageLength, key, blockSize):
    # Decrypts a list of encrypted block ints into the original message
    # string. The original message length is required to properly decrypt
    # the last block. Be sure to pass the PRIVATE key to decrypt.
    decryptedBlocks = []
    n, d = key

解密的数学与加密的数学相同，除了整数块被提升到d而不是e，正如你在第 90 行看到的。

    for block in encryptedBlocks:
        # plaintext = ciphertext ^ d mod n
        decryptedBlocks.append(pow(block, d, n))

解密的块连同messageLength和blockSize参数被传递给getTextFromBlocks()，以便decryptMessage()在第 91 行返回解密的明文作为字符串。

    return getTextFromBlocks(decryptedBlocks, messageLength, blockSize)

现在，您已经了解了使加密和解密成为可能的数学，让我们看看readKeyFile()函数如何读取公钥和私钥文件来创建我们传递给encryptMessage ()和decryptMessage()的元组值。

从自己的密钥文件中读入公钥和私钥

调用readKeyFile()函数从用makePublicPrivateKeys.py程序创建的密钥文件中读取值，该程序是我们在第 23 章中创建的。要打开的文件名传递给keyFilename，文件必须和publicKeyCipher.py程序在同一个文件夹。

第 97 到 99 行打开这个文件，将内容作为一个字符串读入到content变量中。

def readKeyFile(keyFilename):
    # Given the filename of a file that contains a public or private key,
    # return the key as a (n,e) or (n,d) tuple value.
    fo = open(keyFilename)
    content = fo.read()
    fo.close()
    keySize, n, EorD = content.split(',')
    return (int(keySize), int(n), int(EorD))

密钥文件将密钥大小以字节存储为n，以及e或d，这取决于密钥文件是用于加密密钥还是解密密钥。正如您在上一章中了解到的，这些值被存储为文本并以逗号分隔，所以我们使用split()字符串方法在逗号处分割content中的字符串。split()返回的列表中有三个条目，第 100 行的多重赋值将这些条目分别放入keySize、n和EorD变量中。

回想一下，content从文件中读取时是一个字符串，而split()返回的列表中的项目也将是字符串值。为了将这些字符串值转换成整数，我们将keySize、n和EorD的值传递给int()。然后，readKeyFile()函数返回三个整数，int(keySize)、int(n)和int(EorD)，您将使用它们进行加密或解密。

将密文写入文件

在第 104 行，encryptAndWriteToFile()函数调用encryptMessage()用密钥加密字符串，并创建包含加密内容的文件。

def encryptAndWriteToFile(messageFilename, keyFilename, message,
       blockSize=None):
    # Using a key from a key file, encrypt the message and save it to a
    # file. Returns the encrypted message string.
    keySize, n, e = readKeyFile(keyFilename)

encryptAndWriteToFile()函数接受三个字符串参数:要写入加密消息的文件名（messageFilename（、要使用的公钥文件名（keyFilename（和要加密的消息（message）。blockSize参数被指定为第四个参数。

加密过程的第一步是通过调用第 107 行上的readKeyFile()从密钥文件中读入keySize、n和e的值。

blockSize参数有一个默认参数None:

    if blockSize == None:
        # If blockSize isn't given, set it to the largest size allowed by
               the key size and symbol set size.
        blockSize = int(math.log(2 ** keySize, len(SYMBOLS)))

如果没有为blockSize参数传递参数，则blockSize将被设置为符号集和密钥大小允许的最大大小。请记住，等式2 ** keySize > len(SYMBOLS) ** blockSize必须为真。为了计算最大可能的块大小，Python 的math.log()函数被调用来计算第 110 行上以len(SYMBOLS)为底的2 ** keySize的对数。

只有当密钥大小等于或大于块大小时，公钥密码的数学运算才能正确工作，所以在继续之前，我们必须在第 112 行检查这一点。

    # Check that key size is large enough for the block size:
    if not (math.log(2 ** keySize, len(SYMBOLS)) >= blockSize):
        sys.exit('ERROR: Block size is too large for the key and symbol
             set size. Did you specify the correct key file and encrypted
             file?')

如果keySize太小，程序退出并显示错误信息。用户必须减小为blockSize传递的值，或者使用更大的密钥。

现在我们有了密钥的n和e值，我们调用第 115 行的函数encryptMessage()，它返回一个整数块列表。

    # Encrypt the message
    encryptedBlocks = encryptMessage(message, (n, e), blockSize)

encryptMessage()函数期望密钥使用两个整数的元组，这就是为什么n和e变量被放在元组中，然后作为第二个参数传递给encryptMessage()。

接下来，我们将加密的块转换成可以写入文件的字符串。为此，我们将这些块连接成一个字符串，每个块用逗号分隔。使用','.join(encryptedBlocks)这样做是行不通的，因为join()只对字符串值的列表有效。因为encryptedBlocks是一个整数列表，我们要先把这些整数转换成字符串:

    # Convert the large int values to one string value:
    for i in range(len(encryptedBlocks)):
        encryptedBlocks[i] = str(encryptedBlocks[i])
    encryptedContent = ','.join(encryptedBlocks)

第 118 行的for循环遍历encryptedBlocks中的每个索引，用整数的字符串形式替换encryptedBlocks[i]处的整数。当循环完成时，encryptedBlocks应该包含一个字符串值列表，而不是一个整数值列表。

然后我们可以将encryptedBlocks中的字符串值列表传递给join()方法，该方法返回列表中连接在一起的字符串，每个字符串由逗号分隔。第 120 行将这个组合字符串存储在encryptedContent变量中。

除了加密的整数块之外，我们还将消息的长度和块大小写入文件:

    # Write out the encrypted string to the output file:
    encryptedContent = '%s_%s_%s' % (len(message), blockSize,
           encryptedContent)

第 123 行修改了encryptedContent变量，将消息的大小作为一个整数len(message)，后面跟着一个下划线、blockSize，另一个下划线，最后是加密的整数块（encryptedContent）。

加密过程的最后一步是将内容写入文件。由messageFilename参数提供的文件名是通过调用第 124 行上的open()创建的。请注意，如果同名文件已经存在，新文件将覆盖它。

    fo = open(messageFilename, 'w')
    fo.write(encryptedContent)
    fo.close()
    # Also return the encrypted string:
    return encryptedContent

通过调用第 125 行的write()方法将encryptedContent中的字符串写入文件。程序写完文件内容后，第 126 行关闭了fo中的文件对象。

最后，encryptedContent中的字符串从第 128 行的函数encryptAndWriteToFile ()返回。（这是为了让调用该函数的代码可以使用该字符串，例如，在屏幕上打印它。）

现在您知道了encryptAndWriteToFile()函数如何加密消息字符串并将结果写入文件。让我们看看程序如何使用readFromFileAndDecrypt()函数来解密一条加密的消息。

从文件中解密

与encryptAndWriteToFile()类似，readFromFileAndDecrypt()函数具有加密消息文件的文件名和密钥文件的文件名的参数。确保传递的是keyFilename的私钥文件名，而不是公钥。

def readFromFileAndDecrypt(messageFilename, keyFilename):
    # Using a key from a key file, read an encrypted message from a file
    # and then decrypt it. Returns the decrypted message string.
    keySize, n, d = readKeyFile(keyFilename)

第一步与encryptAndWriteToFile()相同:调用readKeyFile()函数获取keySize、n和d变量的值。

第二步是读入文件的内容。第 138 行打开messageFilename文件进行读取。

    # Read in the message length and the encrypted message from the file:
    fo = open(messageFilename)
    content = fo.read()
    messageLength, blockSize, encryptedMessage = content.split('_')
    messageLength = int(messageLength)
    blockSize = int(blockSize)

第 139 行的read()方法调用返回文件全部内容的字符串，如果您在记事本或 TextEdit 之类的程序中打开文本文件，复制全部内容，并将其作为字符串值粘贴到您的程序中，您将会看到这样的结果。

回想一下，加密文件的格式有三个由下划线分隔的整数:一个表示消息长度的整数，一个表示所用块大小的整数，以及加密的整数块。第 140 行调用split()方法返回这三个值的列表，多重赋值技巧将这三个值分别放入messageLength、blockSize和encryptedMessage变量中。

因为split()返回的值是字符串，所以第 141 行和第 142 行使用int()将messageLength和blockSize分别转换为它们的整数形式。

readFromFileAndDecrypt()函数还在第 145 行检查块大小是否等于或小于密钥大小。

    # Check that key size is large enough for the block size:
    if not (math.log(2 ** keySize, len(SYMBOLS)) >= blockSize):
        sys.exit('ERROR: Block size is too large for the key and symbol
             set size. Did you specify the correct key file and encrypted
             file?')

这种检查应该总是通过的，因为如果块太大，一开始就不可能创建加密文件。很可能为参数keyFilename指定了错误的私钥文件，这意味着该密钥无论如何都无法正确解密该文件。

encryptedMessage字符串包含许多用逗号连接在一起的块，我们将其转换回整数并存储在变量encryptedBlocks中。

    # Convert the encrypted message into large int values:
    encryptedBlocks = []
    for block in encryptedMessage.split(','):
        encryptedBlocks.append(int(block))

第 150 行的for循环遍历通过调用encryptedMessage上的split()方法创建的列表。该列表包含单个块的字符串。每次执行第 151 行时，这些字符串的整数形式被附加到encryptedBlocks列表（第 149 行的空列表）。在第 150 行的for循环完成后，encryptedBlocks列表应该包含encryptedMessage字符串中数字的整数值。

在第 154 行，encryptedBlocks中的列表连同messageLength、私钥（两个整数n和d的元组值）和块大小一起被传递给decryptMessage()函数。

    # Decrypt the large int values:
    return decryptMessage(encryptedBlocks, messageLength, (n, d),
           blockSize)

第 154 行的decryptMessage()函数返回解密消息的单个字符串值，该值本身是从readFileAndDecrypt()返回的值。

调用main()函数

最后，如果publicKeyCipher.py作为一个程序运行，而不是作为一个模块被另一个程序导入，那么第 159 和 160 行调用main()函数。

# If publicKeyCipher.py is run (instead of imported as a module), call
# the main() function.
if __name__ == '__main__':
    main()

这就完成了我们对publicKeyCipher.py程序如何使用公钥密码执行加密和解密的讨论。

总结

恭喜你，你完成了这本书！没有“破解公钥密码”这一章，因为对公钥密码的简单攻击不需要几万亿年。

在这一章中，RSA 算法被大大简化了，但它仍然是专业加密软件中使用的真正的密码。例如，当你登录一个网站或在互联网上购物时，像这样的密码可以防止任何人截获你的网络流量，从而保护你的密码和信用卡号码。

虽然用于专业加密软件的基本数学与本章所描述的相同，但是你不应该使用这个程序来保护你的秘密文件。针对像publicKeyCipher.py这样的加密程序的攻击非常复杂，但它们确实存在。（例如，因为创建的随机数random.randint()不是真正随机的，并且是可以预测的，黑客可以找出哪些数字被用作你的私钥的质数。）

本书中讨论的所有密码都可以被破解，变得一文不值。一般来说，避免编写自己的加密代码来保护您的秘密，因为您可能会在这些程序的实现中犯一些微妙的错误。黑客和间谍机构可以利用这些错误来破解你的加密信息。

只有当除了密钥之外的所有内容都可以被揭示，同时仍然保持消息的机密性时，密码才是安全的。你不能依赖于密码分析者无法使用相同的加密软件或者不知道你使用的是哪种密码。永远假设敌人了解系统！

专业加密软件是由花了数年时间研究各种密码的数学和潜在弱点的密码学家编写的。即使这样，他们编写的软件也会被其他密码学家检查，以检查错误或潜在的弱点。你完全有能力学习这些密码系统和密码数学。不是成为最聪明的黑客，而是花时间去学习成为最有知识的黑客。

我希望这本书给了你成为精英黑客和程序员所需要的基础。编程和密码学有比这本书涵盖的更多的东西，所以我鼓励你探索和学习更多！我强烈推荐西蒙·辛格的《密码本:从古埃及到量子密码术的秘密科学》,这是一本关于密码术通史的伟大著作。你可以去 https://www.nostarch.com/crackingcodes/的查看其他书籍和网站的列表，了解更多关于密码学的知识。请将您的编程或加密问题通过电子邮件发送到[email@protection](/cdn-cgi/l/email-protection#ee8f82ae8780988b809a99879a869e979a868180c08d8183）或发布到[reddit.com/r/inventwithpython](https://reddit.com/r/inventwithpython/）。

祝你好运！