sklearn实战01:决策树
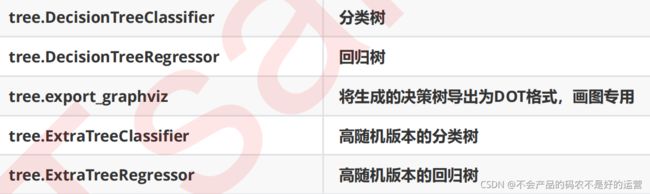
1 模块sklearn.tree的使用
1.1 模块介绍
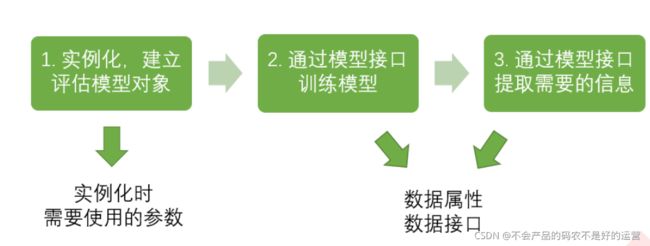
1.2 使用流程
from sklearn import tree #导入需要的模块
clf = tree.DecisionTreeClassifier() #实例化
clf = clf.fit(X_train,y_train) #用训练集数据训练模型
result = clf.score(X_test,y_test) #导入测试集,从接口中调用需要的信息
2 重要参数
2.1 criterion
Criterion这个参数正是用来决定不纯度的计算方法的。sklearn提供了两种选择:
1)输入”entropy“,使用信息熵(Entropy)
2)输入”gini“,使用基尼系数(Gini Impurity)

from sklearn import tree
from sklearn import datasets
from sklearn.model_selection import train_test_split
import graphviz
wine = datasets.load_wine()
# print(wine) 字典形式
# print(wine.data)
# print(wine.data.shape) #(178, 13)一共有13个特征
# print(wine.target)
x_train, x_test, y_train, y_test = train_test_split(wine.data, wine.target, test_size=0.3)
# test_size=0.3——>0.3是训练接,0.7是测试集
# print(x_train)
print(x_train.shape) # (124, 13)
print(y_train.shape) # (124,)
clf = tree.DecisionTreeClassifier(criterion="entropy")
#实例化
clf = clf.fit(x_train, y_train) #训练模型
score = clf.score(x_test, y_test) # 返回预测的精确度accuracy
print(score) # 0.7962962962962963
feature_name = ['酒精', '苹果酸', '灰', '灰的碱性', '镁', '总酚', '类黄酮', '非黄烷类酚类', '花青素', '颜色强度', '色调', 'od280/od315稀释葡萄酒', '脯氨酸']
#将特征值改为中文
dot_data = tree.export_graphviz(clf,
out_file='tree.dot',
feature_names=feature_name,
class_names=['琴酒', '雪莉', '贝尔摩德'],
filled=True, #填充颜色
rounded=True #边框略圆
)
with open('tree.dot', encoding='utf-8') as f:
dot_grapth = f.read()
graph = graphviz.Source(dot_grapth.replace("helvetica", "MicrosoftYaHei"))
#为了显示中文,所以只能改变dot文件里的字体
graph.render(r'D:/wine')
graph.view()
2.2 random_state & splitter
训练集和测试集划分每次都是随机的喔,所以实验结果每次都不同
决策树在形成时,分支的时候是通过计算每个节点的不纯度来选取节点,是通过优化每个节点来形成的,但是最优的节点不一定能形成最优的树。
每次建树的时候都是通过选取不同的特征值来形成不同的树。但是每次返回的最优的树都不同。
所以可以通过固定一个种子数来固定最优树模型。
random_state用来设置分枝中的随机模式的参数,默认None,在高维度时随机性会表现更明显,低维度的数据 (比如鸢尾花数据集),随机性几乎不会显现。输入任意整数,会一直长出同一棵树,让模型稳定下来。
splitter也是用来控制决策树中的随机选项的,有两种输入值,输入”best",决策树在分枝时虽然随机,但是还是会优先选择更重要的特征进行分枝(重要性可以通过属性feature_importances_查看),输入“random",决策树在分枝时会更加随机,树会因为含有更多的不必要信息而更深更大,并因这些不必要信息而降低对训练集的拟合。
clf = tree.DecisionTreeClassifier(criterion="entropy",
random_state=30,
splitter='random')
2.3 剪枝参数
2.3.1 max_depth
限制树的最大深度,超过设定深度的树枝全部剪掉 这是用得最广泛的剪枝参数,在高维度低样本量时非常有效。决策树多生长一层,对样本量的需求会增加一倍,所以限制树深度能够有效地限制过拟合。实际使用时,建议从=3开始尝试,看看拟合的效 果再决定是否增加设定深度。
2.3.2 min_samples_leaf & min_samples_split min_samples_leaf
限定,一个节点在分枝后的每个子节点都必须包含至少min_samples_leaf个训练样本,否则分 枝就不会发生,或者,分枝会朝着满足每个子节点都包含min_samples_leaf个样本的方向去发生。
一般搭配max_depth使用,在回归树中有神奇的效果,可以让模型变得更加平滑。这个参数的数量设置得太小会引 起过拟合,设置得太大就会阻止模型学习数据。一般来说,建议从5开始使用。
min_samples_split限定,一个节点必须要包含至少min_samples_split个训练样本,这个节点才允许被分枝,否则 分枝就不会发生。
test = []
for i in range(10):
clf = tree.DecisionTreeClassifier(max_depth=i + 1,
criterion="entropy",
random_state=30,
splitter='random',
)
clf = clf.fit(x_train, y_train)
score = clf.score(x_test, y_test) # 返回预测的精确度accuracy
test.append(score)
plt.plot(range(1, 11), test, color='red', label='max_depth')
plt.legend()
plt.show()
2.3.3 max_features & min_impurity_decrease
一般搭配max_depth使用
max_features限制分枝时考虑的特征个数,超过限制个数的特征都会被舍弃。和max_depth异曲同工
max_features是用来限制高维度数据的过拟合的剪枝参数,但其方法比较暴力,是直接限制可以使用的特征数量而强行使决策树停下的参数,在不知道决策树中的各个特征的重要性的情况下,强行设定这个参数可能会导致模型学习不足。如果希望通过降维的方式防止过拟合,建议使用PCA,ICA或者特征选择模块中的降维算法。
min_impurity_decrease限制信息增益的大小,(信息增益是用父节点的信息熵-子节点的信息熵)信息增益小于设定数值的分枝不会发生。这是在0.19版本中更新的功能,在0.19版本之前时使min_impurity_split。
剪枝参数可以通过学习曲线来找到最优参数
无论如何,剪枝参数的默认值会让树无尽地生长,这些树在某些数据集上可能非常巨大,内存的消耗也非常巨大。所以如果你手中的数据集非常巨大,你已经预测到无论如何你都是要剪枝的,那提前设定这些参数来控制树的 复杂性和大小会比较好。
2.3.4 目标权重参数
class_weight & min_weight_fraction_leaf
在银行要 判断“一个办了信用卡的人是否会违约”,就是是vs否(1%:99%)的比例。这种分类状况下,即便模型什么也不 做,全把结果预测成“否”,正确率也能有99%。因此我们要使用class_weight参数对样本标签进行一定的均衡,给少量的标签更多的权重,让模型更偏向少数类,向捕获少数类的方向建模。
有了权重之后,样本量就不再是单纯地记录数目,而是受输入的权重影响了,因此这时候剪枝,就需要搭配min_ weight_fraction_leaf这个基于权重的剪枝参数来使用。另请注意,基于权重的剪枝参数(例如min_weight_ fraction_leaf)将比不知道样本权重的标准(比如min_samples_leaf)更少偏向主导类。如果样本是加权的,则使用基于权重的预修剪标准来更容易优化树结构,这确保叶节点至少包含样本权重的总和的一小部分。
2.4 重要的属性和接口
sklearn中许多算法的接口都是相似的,比如说我们之前已经用到的fit和score,几乎对每个算法都可以使用。除了这两个接口之外,决策树最常用的接口还有apply和predict。
3 回归树
3.1 参数
回归树衡量分枝质量的指标,支持的标准有三种: 1)输入"mse"使用均方误差mean squared error(MSE),父节点和叶子节点之间的均方误差的差额将被用来作为 特征选择的标准,这种方法通过使用叶子节点的均值来最小化L2损失
决策树概述+模块介绍+重要参数(criterion+random_state&splitter+减枝参数+目标权重参数)+回归树(参数+实例+拟合正弦曲线)+泰坦尼克号生存者预测实例
2)输入“friedman_mse”使用费尔德曼均方误差,这种指标使用弗里德曼针对潜在分枝中的问题改进后的均方误差
3)输入"mae"使用绝对平均误差MAE(mean absolute error),这种指标使用叶节点的中值来最小化L1损失 属性中最重要的依然是feature_importances_,接口依然是apply, fit, predict, score最核心。
在回归树中,MSE不只是我们的分枝质量衡量指标,也是我们最常用的衡 量回归树回归质量的指标,当我们在使用交叉验证,或者其他方式获取回归树的结果时,我们往往选择均方误差作 为我们的评估(在分类树中这个指标是score代表的预测准确率)。在回归中,我们追求的是,MSE越小越好。然而,回归树的接口score返回的是R平方,并不是MSE。
决策树概述+模块介绍+重要参数(criterion+random_state&splitter+减枝参数+目标权重参数)+回归树(参数+实例+拟合正弦曲线)+泰坦尼克号生存者预测实例
y尖儿是标签的平均值。虽然均方误差永远为正,但是sklearn当中使用均方误差作为评判标准时,却是计算”负均方误 差“(neg_mean_squared_error)。这是因为sklearn在计算模型评估指标的时候,会考虑指标本身的性质,均方误差本身是一种误差,所以被sklearn划分为模型的一种损失(loss),因此在sklearn当中,都以负数表示。真正的均方误差MSE的数值,其实就是neg_mean_squared_error去掉负号的数字。
3.2 交叉验证
交叉验证是用来验证模型稳定性的一种指标。交叉验证是用来观察模型的稳定性的一种方法,我们将数据划分为n份,依次使用其中一份作为测试集,其他n-1份 作为训练集,多次计算模型的精确性来评估模型的平均准确程度。训练集和测试集的划分会干扰模型的结果,因此用交叉验证n次的结果求出的平均值,是对模型效果的一个更好的度量。
3.3 波斯顿房价
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor
boston = load_boston()
regression = DecisionTreeRegressor(random_state=0)
#score = cross_val_score(regression, boston.data, boston.target, cv=10)
#cv=10将我们的数据划分为10组,做10次交叉验证,通常等于
score = cross_val_score(regression, boston.data, boston.target, cv=10, scoring='neg_mean_squared_error')
print(score)
#[ 0.52939335 0.60461936 -1.60907519 0.4356399 0.77280671 0.40597035 0.23656049 0.38709149 -2.06488186 -0.95162992]
#给了十个小于1的数值
#[-16.41568627 -10.61843137 -18.30176471 -55.36803922 -16.01470588 -44.70117647 -12.2148 -91.3888 -57.764 -36.8134 ]
#将score换做MES时,结果明显变大了
3.4 拟合正弦曲线
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
rng = np.random.RandomState(1) #随机种子
#print(rng)这是一个迭代器
#a = rng.rand(80, 1)
#print(a)
x = np.sort(5 * rng.rand(80, 1), axis=0)
#随机生成二维数组,80行1列
#print(x)
y = np.sin(x).ravel() #生成正弦曲线
#print(y)
y[::5] += 3 * (0.5 - rng.rand(16)) #在正弦曲线上加噪声
#随机生成16个数
#plt.scatter(x, y, edgecolor="black", c="darkorange", label="data")
#plt.show()
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(x, y)
regr_2.fit(x, y)
x_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
#[:, np.newaxis]是类切片操作,主要的作用是增加维度,将一维数组增加成二维数组
print(x_test.shape)
y_1 = regr_1.predict(x_test)
y_2 = regr_2.predict(x_test)
#print(y_1)
#print(y_2)
plt.figure()
plt.scatter(x, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(x_test, y_1, color="cornflowerblue", label="max_depth=2", linewidth=2)
plt.plot(x_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
4 泰坦尼克号生存者预测
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import numpy as np
data = pd.read_csv('data.csv')
#print(data)
#print(data.head(5))
#print(data.info())
'''
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 891 non-null int64
1 Survived 891 non-null int64
2 Pclass 891 non-null int64
3 Name 891 non-null object
4 Sex 891 non-null object
5 Age 714 non-null float64
6 SibSp 891 non-null int64
7 Parch 891 non-null int64
8 Ticket 891 non-null object
9 Fare 891 non-null float64
10 Cabin 204 non-null object
11 Embarked 889 non-null object
'''
#通过观察可知Name、Sex、Ticket、Cabin、Embarked是中文,以及Cabin缺失值较多
#先drop掉不相关的列
data.drop(['Cabin', 'Name', 'Ticket'], inplace=True, axis=1) #axis=1——>删除列
#print(data)
#处理缺失值
data['Age'] = data['Age'].fillna(data['Age'].mean())
#print(data.info())
'''
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 891 non-null int64
1 Survived 891 non-null int64
2 Pclass 891 non-null int64
3 Sex 891 non-null object
4 Age 891 non-null float64
5 SibSp 891 non-null int64
6 Parch 891 non-null int64
7 Fare 891 non-null float64
8 Embarked 889 non-null object
'''
#此时可以观察到有两条数据集是为空,直接dropna
data = data.dropna()
#print(data.info())
#将中文转换为数字
#print(data['Embarked'].unique()) #['S' 'C' 'Q']
labels = data['Embarked'].unique().tolist()
#print(labels) #['S', 'C', 'Q']
data['Embarked'] = data['Embarked'].apply(lambda x: labels.index(x))
#将labels转换为索引值
#print(labels.index('S')) #0
data['Sex'] = (data['Sex'] == 'felman').astype('int')
#将性别转换为整数0/1
#print(data['Sex'])
#print(data.head())
#设置特征值和标签
x = data.loc[:, data.columns != 'Survived']
y = data.loc[:, data.columns == 'Survived']
#print(x)
#print(y)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)
#修正测试集和训练集的索引
for i in [x_train, x_test, y_train, y_test]:
i.index = range(i.shape[0])
#print(x_train.head())
#print(x_test.head())
#寻找最恰当的max_depth方法
tr = []
te = []
for i in range(10):
clf = DecisionTreeClassifier(random_state=15,
max_depth=i+1,
criterion='entropy')
clf = clf.fit(x_train, y_train)
score_tr = clf.score(x_train, y_train)
score_te = cross_val_score(clf, x, y, cv=10).mean()
#在每一个参数下都进行10次交叉验证,一共实验100次
tr.append(score_tr)
te.append(score_te)
print(max(te))
plt.plot(range(1, 11), tr, color='red', label='train')
plt.plot(range(1, 11), te, color='blue', label='test')
plt.xticks(range(1, 11))
plt.legend()
plt.show()
通过for循环寻找最合适的max_depth参数是一种办法,可以通过网格搜索来查找!
网格搜索
能够帮助我们同时调整多个参数的技术——枚举技术
#gini_thresholds = np.linespace(0, 0.5, 20)
#entropy_thresholds = np.linespace(0, 1, 20)
parameters = {'splitter': ('best', 'random'),
'criterion': ("gini", "entropy"),
'max_depth': [*range(1, 10)],
'min_samples_leaf': [*range(1, 50, 5)],
'min_impurity_decrease': [*np.linspace(0, 0.5, 20)]#生成20个0-0.5之间的数
}
clf = DecisionTreeClassifier(random_state=25)
GS = GridSearchCV(clf, parameters, cv=10)
GS.fit(x_train, y_train)
print(GS.best_params_)#从输入的参数和参数取值的列表中返回最佳组合
print(GS.best_score_)#网格搜索后的模型的评判标准
#{'criterion': 'gini', 'max_depth': 7, 'min_impurity_decrease': 0.0, 'min_samples_leaf': 6, 'splitter': 'best'}
#0.7153865847414236
网格搜索是有弊端的,它只能按照列出来的参数进行搜索匹配最佳组合,但是不能舍弃参数。所以到底把什么内容放在网格搜索的参数里是值得揣摩思考的。