NJUPT算法分析与设计期末考试202.12.1
NJUPT算法分析与设计期末考试2021.11.24
- 判断
- 简答
-
- 1.算法是什么?算法的时间复杂度是什么?衡量的原则,标准,工具
- 2.分支限界法扩展活节点的方式有哪两种,有什么差别?
- 3.回溯法搜索子集树,排列树的算法。P124
-
- 回溯法搜索子集树
- 回溯法搜索排列树
- 4.剪枝策略:什么是约束函数,什么是限界函数,区别是什么?
- 5.递归分治策略和动态规划策略的相同和不同
- 算法设计
-
- 一、递归+分治(修改的二分搜索问题)
-
- 问题描述
- 1.二分搜索的基本思想
- 2.实现
- 二.DP(最大字段和问题)
-
- 问题描述
- 1.最优子结构递推方程
- 2.算法框架
- 3.实例推导
- 4.时间复杂度
- 三.贪心(最优装载问题)
-
- 问题描述
- 1.数学模型
- 2.算法框架
- 3.时间复杂度
- 4.正确性分析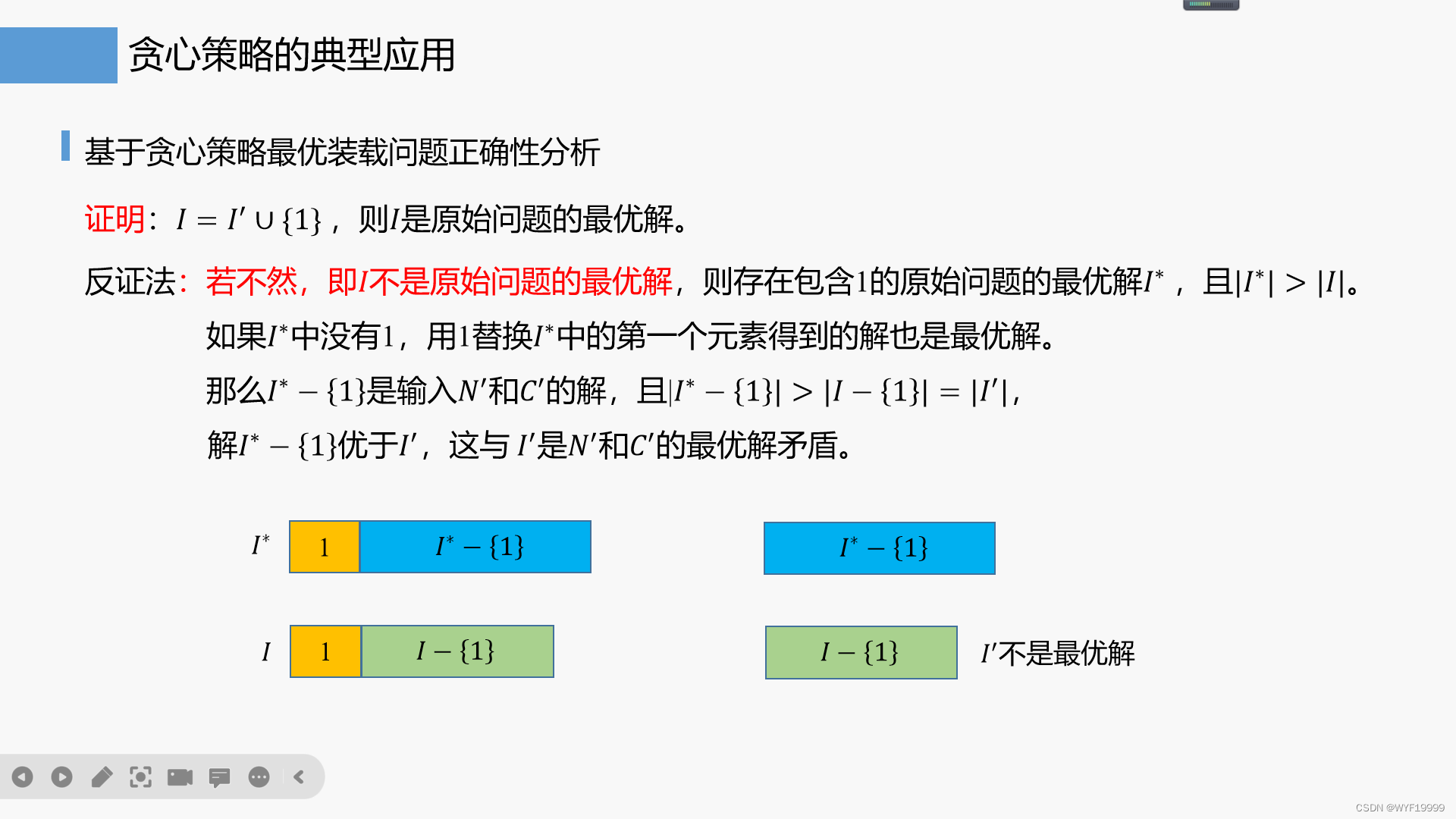
- 四.回溯和分支限界(旅行商问题)
-
- 1.解空间是子集树还是排列树?
- 2.回溯法求解的过程
- 3.分支限界法求解的过程
用书:计算机算法设计与分析(第五版)
判断10题30分
简答5题30分
算法设计4*10=40分
判断
1.程序、算法、软件是不完全等价的。
2.最优化问题不是都可以用动态规划来求解,使用动态规划要满足(子问题间有依赖关系;有最优子结构)。
3.分治策略是先把复杂的问题自顶向下求解,然后自底向上合并,不一定要用递归,用迭代也可以。
4.动态规划能求解的问题,贪心策略不一定能求解,反之也不行。(如0-1背包问题可以用动态规划但不能用贪心;背包问题可以用贪心但不能用递归)。
5.两个序列的公共子序列和最长公共子序列都不唯一。
6.棋盘覆盖问题8*8的棋盘用(64-1)/3=21块骨牌。
7.哈夫曼算法是贪心算法,每次选择频率最高的两个节点合并成子树。
8.不同的排序算法针对不同实例,速度效率不一样。
9.常用的时间复杂度。
简答
1.算法是什么?算法的时间复杂度是什么?衡量的原则,标准,工具
(PPT ch1)
- 算法的定义:算法是对特定问题求解步骤的一种描述,它是由若干指令组成的有穷序列,特性(输入、输出、有穷、确定、可行)
- 时间算法复杂度:是对算法执行所需的时间的一种度量;
- 原则标准:统一机器性能,分析最坏情况
- 工具:渐进分析方法:忽略T(n)的系数与低阶项,仅关注高阶项;
2.分支限界法扩展活节点的方式有哪两种,有什么差别?
- 队列式(FIFO)分支限界法:按照队列先进先出(FIFO)原则选取下一个节点为扩展节点。
- 优先队列式分支限界法:按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。
3.回溯法搜索子集树,排列树的算法。P124
http://wjhsh.net/xymqx-p-3702921.html
回溯法搜索子集树
//回溯法搜索子集树
void Backtrack(int t){
{
if(t>n)
output(x);
else
{
for(int i=0;i<=1;i++) //子集树只考虑取或者不取,所以解向量只有0或1;
{
x[t]=i;
if(Constraint(t)&&Bound(t))
Backtrack(t+1);
}
}
}
回溯法搜索排列树
//回溯法搜索排列树
void Backtrack(int t){
{
if(t>n)
output(x);
else
{
for(int i=t;i<=n;i++)
{
Swap(x[t],x[i]); //把当前递归层的元素依次和其他元素交换
if(Constraint(t)&&Bound(t))
Backtrack(t+1); //进入下一层递归
Swap(x[t],x[i]); //回溯时候恢复之前的交换
}
}
}
4.剪枝策略:什么是约束函数,什么是限界函数,区别是什么?
约束函数:在扩展节点处剪去不满足约束的子树
限界函数:用限界函数剪去不能得到最优解的子树
都是剪去不必要搜索的子树,约束函数剪去的是无解的子树,而限界函数剪去的是得不到最优解的子树。
5.递归分治策略和动态规划策略的相同和不同
相同:都是把大问题转化为子问题来解决
不同:递归分治的子问题相互独立,动态规划的子问题是相互依赖的,有最优子结构
算法设计
一、递归+分治(修改的二分搜索问题)
问题描述
改写二分搜索算法,使得当搜索元素x不在数组中时,返回小于x的最大元素位置i和大于x的元素位置j。当搜索元素在数组中时,i和j相同,均为x在数组中的位置。
1.二分搜索的基本思想
二分搜索方法充分利用了元素间的次序关系,采用分治策略,可以在最坏情况下用O(logn)时间完成搜索任务,将n个元素分成个数大致相同的两半,取a[n/2]与x进行比较,若x=a[n/2],则找到x,算法终止;x=a[n/2],则只在数组左半部递归的搜索;若x>a[n/2],则只在数组右半部递归的搜索。
2.实现
int Binary_Search(int a[],int length, int x) //a是搜索数组,x为搜索元素
{
int i = 0, j = 0; //用来输出结果
int flag = -1;//标志位
int high = length - 1; // 数组的右边界
int mid = 0; //中间值的下标
int low = 0; //数组的左边界
while (low <= high)
{
mid = (low + high) / 2;
if (a[mid] == x)
{
flag = middle;
}
if (a[mid] < x)
{
low = mid + 1;
}
else
{
top = mid - 1;
}
}
if (flag == -1)
{
i = high;
j = low;
}
else
{
i = j = flag ;
}
cout<<i<<j;
return 0;
}
二.DP(最大字段和问题)
问题描述
1.最优子结构递推方程
2.算法框架
void dp(int D[],int X[],int R[],n)
{ //X[i]存储第i个数字的值,D[i]表示以x[i]为开头的最大字段和的值;R[]
D[n]=X[n]; //最后一位开头的最长子段和只能是本身
R[n]=n; //最后一位的右端点只能是n
for(int i=n-1;i>=n;i--)
{ //最后一个位置的数字作为初值,从倒数第二个位置开始从后向前递推
if(D[i+1]>0)
D[i]=X[i]+D[i+1]; //如果以i+1位置开头的最大字段和大于0,那么以i位置开头最大字段和就是当前位置的数值+后面的最大字段和的值。
else{
D[i]=X[i]; //如果以i+1位置开头的最大字段和小于0;
R[i]=i; //此时最大字段和的右端就是i本身
}
}
}
void MaxSum(int D[],int R[]}
{
S_max=D[1] //先假设以第一个数字开头的最大字段和为全局最大字段和
for(int i=2;i<=n;i++)
{
if(S_max<D[i])
{
l=i;
r=R[i];
}
}
cout<<"最大字段和从位置"<<l<<"到位置"<<r<<"其值为"<<D[l];
}
3.实例推导
4.时间复杂度
O(n)
三.贪心(最优装载问题)
问题描述
1.数学模型
2.算法框架
void Loading(int x[], Type w[], Type c, int n)
{
int *t = new int [n+1]; //动态数组t用来存放排序后的货物
Sort(w, t, n); //将集装箱按重量把数组w非减排序存放到数组t中
for ( int i = 1; i <= n; i++ )
x[i] = 0; //决策变量初始化
for ( int i = 1; i <= n && w[t[i]] <= c; i++ ) {
x[t[i]] = 1; //决策变量的对应位置置为1
c -= w[t[i]]; //更新当前的荷载量
} //在剩余集装箱中选择最轻的装船,直至超重
}
3.时间复杂度
O(nlogn) 主要来自把货物按重量排序的算法sort()
4.正确性分析

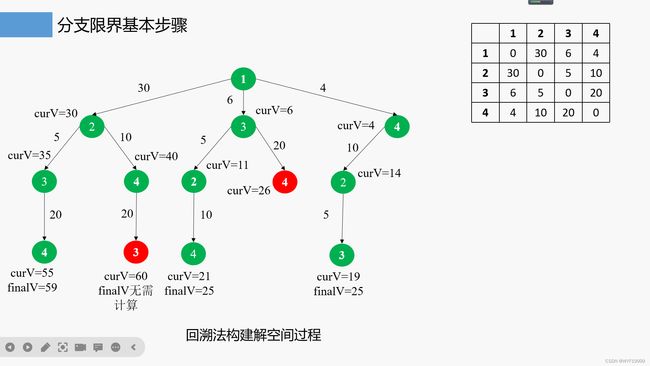
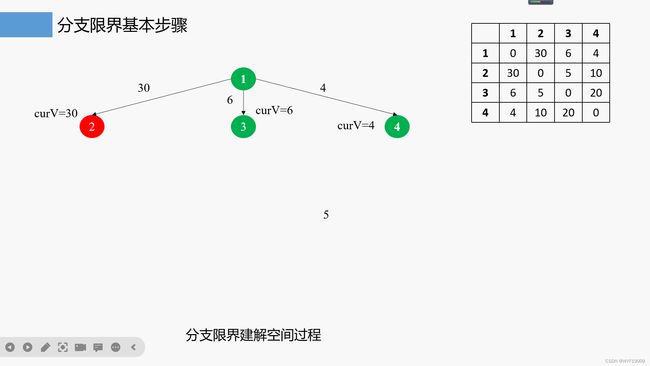
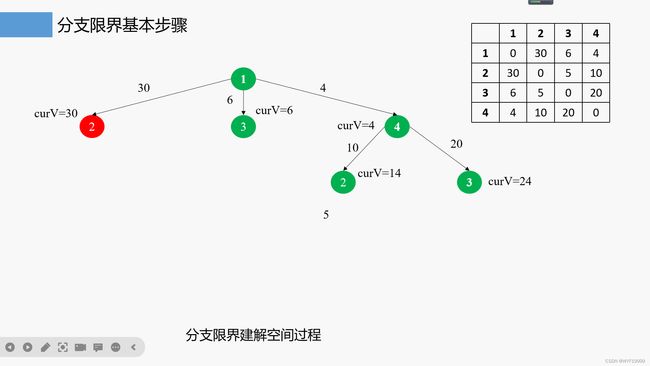
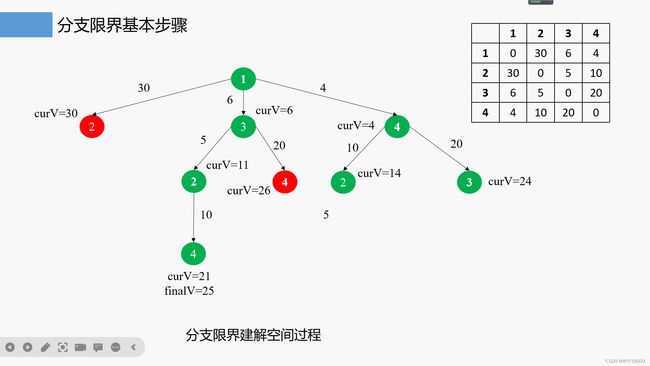
四.回溯和分支限界(旅行商问题)
1.解空间是子集树还是排列树?
答:排列树,因为每个城市都要访问。
2.回溯法求解的过程
//旅行商问题回溯算法的实现
//形参t是回溯的深度,从2开始
void Backtrack(int t)
{
//到达叶子结点的父结点
if(t==n)
{
if(a[x[n-1]][x[n]]!= NoEdge && a[x[n]][1]!= NoEdge &&
(cc + a[x[n-1]][x[n]]+a[x[n]][1]<bestc||bestc== NoEdge))
{
for(int i=1; i<=n; i++)
bestx[i] = x[i];
bestc = cc + a[x[n-1]][x[n]] + a[x[n]][1];
}
return;
}
else
{
for(int i=t; i<=n; i++)
{
if(a[x[t-1]][x[i]]!= NoEdge &&
(cc + a[x[t-1]][x[i]]< bestc||bestc == NoEdge))
{
swap(x[t],x[i]);
cc += a[x[t-1]][x[t]];
Backtrack(t+1);
cc -= a[x[t-1]][x[t]];
swap(x[t],x[i]);
}
}
}
}
3.分支限界法求解的过程
//旅行商问题分支限界法的实现
template <class Type>
Type Traveling<Type>::BBTSP(int *v, Type **G, int tn, Type tNoEdge)
{
priority_queue<MinHeapNode<Type> > pq;
MinHeapNode<Type> E, N;
Type bestc, cc, rcost, MinSum, *MinOut, b;
int i, j;
a = G;
n = tn;
NoEdge = tNoEdge;
MinSum = 0; //最小出边费用和
MinOut = new Type[n+1]; //计算MinOut[i]=顶点i的最小出边费用
for(i = 1; i <= n; i++)
{
MinOut[i] = NoEdge;
for(j = 1; j <= n; j++)
if(a[i][j] != NoEdge && (a[i][j] < MinOut[i] || MinOut[i] == NoEdge))
MinOut[i] = a[i][j];
if(MinOut[i] == NoEdge) //无回路
return NoEdge;
MinSum += MinOut[i];
}
//初始化
E.s = 0;
E.cc = 0;
E.rcost = MinSum;
E.x = new int[n];
for(i = 0; i < n; i++)
E.x[i] = i+1;
bestc = NoEdge;
//搜索排列空间树
while(E.s < n-1) //非叶结点
{
if(E.s == n-2) //当前扩展结点是叶结点的父结点 再加2条边构成回路
{ //所构成回路是否优于当前最优解
if(a[E.x[n-2]][E.x[n-1]] != NoEdge && a[E.x[n-1]][1] != NoEdge &&
(E.cc+a[E.x[n-2]][E.x[n-1]]+a[E.x[n-1]][1] < bestc || bestc==NoEdge))
{
//费用更小的路
bestc = E.cc + a[E.x[n-2]][E.x[n-1]] + a[E.x[n-1]][1];
E.cc = bestc;
E.lcost = bestc;
E.s++;
pq.push(E);
}
else
delete []E.x; //舍弃扩展结点
}
else //产生当前扩展结点儿子结点
{
for(i = E.s+1; i < n; i++)
if(a[E.x[E.s]][E.x[i]] != NoEdge)
{
//可行儿子结点
cc = E.cc + a[E.x[E.s]][E.x[i]]; //当前费用
rcost = E.rcost - MinOut[E.x[E.s]]; //更新最小出边费用和
b = cc + rcost; //下界
if(b < bestc || bestc == NoEdge) //子树可能含最优解 结点插入最小堆
{
N.s = E.s + 1;
N.cc = cc;
N.lcost = b;
N.rcost = rcost;
N.x = new int[n];
for(j = 0; j < n; j++)
N.x[j] = E.x[j];
N.x[E.s+1] = E.x[i]; //获得新的路径
N.x[i] = E.x[E.s+1];
pq.push(N); //加入优先队列
}
}
delete []E.x; //完成结点扩展
}
if(pq.empty()) //堆已空
break;
E = pq.top(); //取下一扩展结点
pq.pop();
}
if(bestc == NoEdge) //无回路
return NoEdge;
for(i = 0; i < n; i++) //将最优解复制到v[1:n]
v[i+1] = E.x[i];
while(pq.size()) //释放最小堆中所有结点
{
E = pq.top();
pq.pop();
delete []E.x;
}
return bestc;
}