基于模糊神经网络的嘉陵江水质评价Matlab代码
1.案例背景
1.1 模糊数学简介
模糊数学是用来描述、研究和处理事物所具有的模糊特征的数学,“模糊”是指它的研究对象,而“数学”是指它的研究方法。
模糊数学中最基本的概念是隶属度和模糊隶属度函数。其中,隶属度是指元素u属于模糊子集f的隶属程度,用uf(u)表示,它是一个在[0,1]之间的数。uf(u)越接近于0,表示u属于模糊子集f的程度越小;越靠近1,表示u属于f 的程度越大。
模糊隶属度函数是用于定量计算元素隶属度的函数,模糊隶属度函数一般包括三角函数、梯形函数和正态函数等。
1.2 T-S模糊模型
T-S模糊系统是一种自适应能力很强的模糊系统,该模型不仅能自动更新,而且能不断修正模糊子集的隶属函数。T-S模糊系统用如下的“if-then”规则形式来定义,在规则为![]() 的情况下,模糊推理如下:
的情况下,模糊推理如下:
1.3 T-S 模糊神经周络
模糊神经网络的学习算法如下。
1.4 嘉陵江水质评价
水质评价是根据水质评价标准和采样水样本各项指标值,通过一定的数学模型计算确定采样水样本的水质等级。水质评价的目的是能够判断出采样水样本的污染等级,为污染防治和水源保护提供依据。
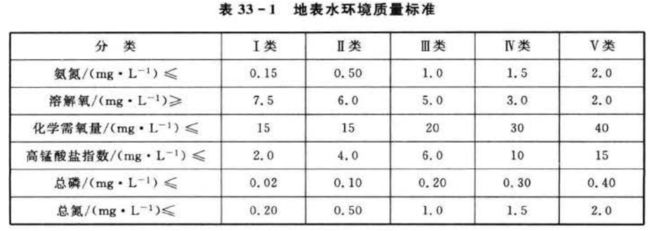
水体水质的分析指标有很多项,主要包括氨氮、溶解氧、化学需氧量、高锰酸盐指数、总磷和总氮六项指标。其中,氨氮是有机物有氧分解的产物,可导致水富营养化现象产生,是水体富营养化的指标。化学需氧量是采用强氧化剂铬酸钾处理水样,消耗的氧化剂量是水中还原性物质多少的指标。高锰酸钾指数同化学需氧量相似,也是反映有机污染的综合指标。溶解氧是溶解在水中的氧,是反映水体自净能力的指标。总磷是水体中磷的浓度含量,是衡量水体富营养化的指标。总氮是水体中氮的含量,也是衡量水体富营养化的指标。各项指标数值对应水质等级如表33-1(地表水环境质量标准)所列。
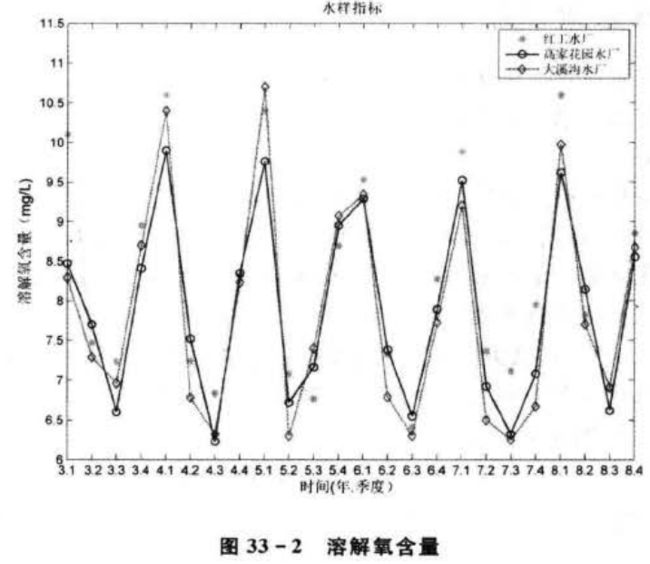
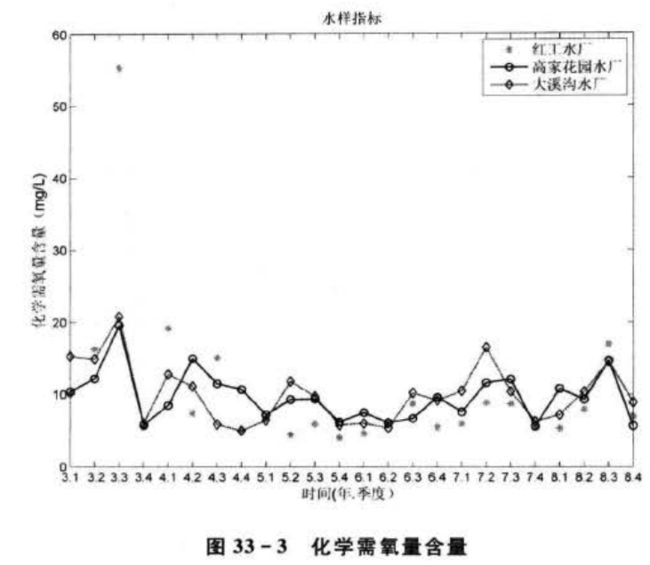
 采取嘉陵江水体样本对嘉陵江水质进行评价,采样取水口为重庆市嘉陵江上游红工水厂、中游高家花园水厂和下游大溪沟水厂,采样时间为2003-—2008年,采样频率为每季度一次。采样水体各项指标变化趋势如图33-1~图33-6所示。
采取嘉陵江水体样本对嘉陵江水质进行评价,采样取水口为重庆市嘉陵江上游红工水厂、中游高家花园水厂和下游大溪沟水厂,采样时间为2003-—2008年,采样频率为每季度一次。采样水体各项指标变化趋势如图33-1~图33-6所示。
从图中可以看出,从 2003年开始,嘉陵江上游、中游、下游各项水质分析指标有所好转,水污染情况得到改善。总体来说,上游红工水厂采样水质优于中游高家花园水厂采样水质,中游高家花园水厂采样水质优于下游大溪沟水厂采样水质。
2.模型建立
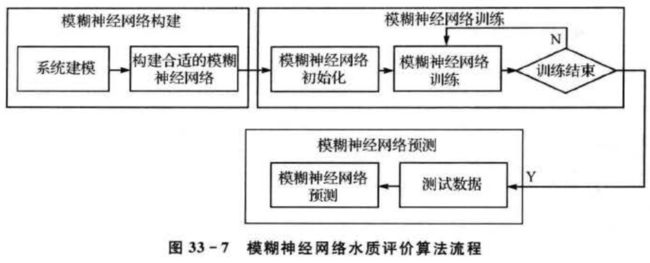
基于T-S模糊神经网络的嘉陵江水质评价算法流程如图33-7所示。其中,模糊神经网络根据训练样本的输人,输出维数确定网络的输入和输出节点数,由于输人数据维数为6,输出数据维数为1,所以确定网络的输人节点个数为6,输出节点个数为1,根据网络输入输出节点个数,人为确定隶属度函数个数为12,因此构建的网络结构为6—12—1,随机初始化模糊隶属度函数中心c,宽度b和系数p0~p6。
模糊神经网络训练用训练数据训练模糊神经网络,由于水质评价真实数据比较难找,所以采用了等隔均匀分布方式内插水质指标标准数据生成样本的方式来生成训练样本,采用的水质指标标准数据来自表 33 -1 ,网络反复训练 100 次。 模糊神经网络预测用训练好的模糊神经网络评价嘉陵江采样水水质等级。
3.编程实现
3.1 代码实现
根据模糊神经网络原理,在 MATLAB中编程实现基于模糊神经网络的水质评价算法。Matlab代码如下:
%% 该代码为基于模糊神经网络的水质评价代码
%% 清空环境变量
clc
clear
%% 参数初始化
xite=0.001;
alfa=0.05;
%网络节点
I=6; %输入节点数
M=12; %隐含节点数
O=1; %输出节点数
%系数初始化
p0=0.3*ones(M,1);p0_1=p0;p0_2=p0_1;
p1=0.3*ones(M,1);p1_1=p1;p1_2=p1_1;
p2=0.3*ones(M,1);p2_1=p2;p2_2=p2_1;
p3=0.3*ones(M,1);p3_1=p3;p3_2=p3_1;
p4=0.3*ones(M,1);p4_1=p4;p4_2=p4_1;
p5=0.3*ones(M,1);p5_1=p5;p5_2=p5_1;
p6=0.3*ones(M,1);p6_1=p6;p6_2=p6_1;
%参数初始化
c=1+rands(M,I);c_1=c;c_2=c_1;
b=1+rands(M,I);b_1=b;b_2=b_1;
maxgen=100; %进化次数
%网络测试数据,并对数据归一化
load data1 input_train output_train input_test output_test
%选连样本输入输出数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
[n,m]=size(input_train);
%% 网络训练
%循环开始,进化网络
for iii=1:maxgen
iii;
for k=1:m
x=inputn(:,k);
%输出层结算
for i=1:I
for j=1:M
u(i,j)=exp(-(x(i)-c(j,i))^2/b(j,i));
end
end
%模糊规则计算
for i=1:M
w(i)=u(1,i)*u(2,i)*u(3,i)*u(4,i)*u(5,i)*u(6,i);
end
addw=sum(w);
for i=1:M
yi(i)=p0_1(i)+p1_1(i)*x(1)+p2_1(i)*x(2)+p3_1(i)*x(3)+p4_1(i)*x(4)+p5_1(i)*x(5)+p6_1(i)*x(6);
end
addyw=yi*w';
%网络预测计算
yn(k)=addyw/addw;
e(k)=outputn(k)-yn(k);
%计算p的变化值
d_p=zeros(M,1);
d_p=xite*e(k)*w./addw;
d_p=d_p';
%计算b变化值
d_b=0*b_1;
for i=1:M
for j=1:I
d_b(i,j)=xite*e(k)*(yi(i)*addw-addyw)*(x(j)-c(i,j))^2*w(i)/(b(i,j)^2*addw^2);
end
end
%更新c变化值
for i=1:M
for j=1:I
d_c(i,j)=xite*e(k)*(yi(i)*addw-addyw)*2*(x(j)-c(i,j))*w(i)/(b(i,j)*addw^2);
end
end
p0=p0_1+ d_p+alfa*(p0_1-p0_2);
p1=p1_1+ d_p*x(1)+alfa*(p1_1-p1_2);
p2=p2_1+ d_p*x(2)+alfa*(p2_1-p2_2);
p3=p3_1+ d_p*x(3)+alfa*(p3_1-p3_2);
p4=p4_1+ d_p*x(4)+alfa*(p4_1-p4_2);
p5=p5_1+ d_p*x(5)+alfa*(p5_1-p5_2);
p6=p6_1+ d_p*x(6)+alfa*(p6_1-p6_2);
b=b_1+d_b+alfa*(b_1-b_2);
c=c_1+d_c+alfa*(c_1-c_2);
p0_2=p0_1;p0_1=p0;
p1_2=p1_1;p1_1=p1;
p2_2=p2_1;p2_1=p2;
p3_2=p3_1;p3_1=p3;
p4_2=p4_1;p4_1=p4;
p5_2=p5_1;p5_1=p5;
p6_2=p6_1;p6_1=p6;
c_2=c_1;c_1=c;
b_2=b_1;b_1=b;
end
E(iii)=sum(abs(e));
end
figure(1);
plot(outputn,'r')
hold on
plot(yn,'b')
hold on
plot(outputn-yn,'g');
legend('实际输出','预测输出','误差')
title('训练数据预测','fontsize',12)
xlabel('样本序号','fontsize',12)
ylabel('水质等级','fontsize',12)
%% 网络预测
%数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
[n,m]=size(inputn_test)
for k=1:m
x=inputn_test(:,k);
%计算输出中间层
for i=1:I
for j=1:M
u(i,j)=exp(-(x(i)-c(j,i))^2/b(j,i));
end
end
for i=1:M
w(i)=u(1,i)*u(2,i)*u(3,i)*u(4,i)*u(5,i)*u(6,i);
end
addw=0;
for i=1:M
addw=addw+w(i);
end
for i=1:M
yi(i)=p0_1(i)+p1_1(i)*x(1)+p2_1(i)*x(2)+p3_1(i)*x(3)+p4_1(i)*x(4)+p5_1(i)*x(5)+p6_1(i)*x(6);
end
addyw=0;
for i=1:M
addyw=addyw+yi(i)*w(i);
end
%计算输出
yc(k)=addyw/addw;
end
%预测结果反归一化
test_simu=mapminmax('reverse',yc,outputps);
%作图
figure(2)
plot(output_test,'r')
hold on
plot(test_simu,'b')
hold on
plot(test_simu-output_test,'g')
legend('实际输出','预测输出','误差')
title('测试数据预测','fontsize',12)
xlabel('样本序号','fontsize',12)
ylabel('水质等级','fontsize',12)
%% 嘉陵江实际水质预测
load data2 hgsc gjhy dxg
%-----------------------------------红工水厂-----------------------------------
zssz=hgsc;
%数据归一化
inputn_test =mapminmax('apply',zssz,inputps);
[n,m]=size(zssz);
for k=1:1:m
x=inputn_test(:,k);
%计算输出中间层
for i=1:I
for j=1:M
u(i,j)=exp(-(x(i)-c(j,i))^2/b(j,i));
end
end
for i=1:M
w(i)=u(1,i)*u(2,i)*u(3,i)*u(4,i)*u(5,i)*u(6,i);
end
addw=0;
for i=1:M
addw=addw+w(i);
end
for i=1:M
yi(i)=p0_1(i)+p1_1(i)*x(1)+p2_1(i)*x(2)+p3_1(i)*x(3)+p4_1(i)*x(4)+p5_1(i)*x(5)+p6_1(i)*x(6);
end
addyw=0;
for i=1:M
addyw=addyw+yi(i)*w(i);
end
%计算输出
szzb(k)=addyw/addw;
end
szzbz1=mapminmax('reverse',szzb,outputps);
for i=1:m
if szzbz1(i)<=1.5
szpj1(i)=1;
elseif szzbz1(i)>1.5&&szzbz1(i)<=2.5
szpj1(i)=2;
elseif szzbz1(i)>2.5&&szzbz1(i)<=3.5
szpj1(i)=3;
elseif szzbz1(i)>3.5&&szzbz1(i)<=4.5
szpj1(i)=4;
else
szpj1(i)=5;
end
end
% %-----------------------------------高家花园-----------------------------------
zssz=gjhy;
inputn_test =mapminmax('apply',zssz,inputps);
[n,m]=size(zssz);
for k=1:1:m
x=inputn_test(:,k);
%计算输出中间层
for i=1:I
for j=1:M
u(i,j)=exp(-(x(i)-c(j,i))^2/b(j,i));
end
end
for i=1:M
w(i)=u(1,i)*u(2,i)*u(3,i)*u(4,i)*u(5,i)*u(6,i);
end
addw=0;
for i=1:M
addw=addw+w(i);
end
for i=1:M
yi(i)=p0_1(i)+p1_1(i)*x(1)+p2_1(i)*x(2)+p3_1(i)*x(3)+p4_1(i)*x(4)+p5_1(i)*x(5)+p6_1(i)*x(6);
end
addyw=0;
for i=1:M
addyw=addyw+yi(i)*w(i);
end
%计算输出
szzb(k)=addyw/addw;
end
szzbz2=mapminmax('reverse',szzb,outputps);
for i=1:m
if szzbz2(i)<=1.5
szpj2(i)=1;
elseif szzbz2(i)>1.5&&szzbz2(i)<=2.5
szpj2(i)=2;
elseif szzbz2(i)>2.5&&szzbz2(i)<=3.5
szpj2(i)=3;
elseif szzbz2(i)>3.5&&szzbz2(i)<=4.5
szpj2(i)=4;
else
szpj2(i)=5;
end
end
% %-----------------------------------大溪沟水厂-----------------------------------
zssz=dxg;
inputn_test =mapminmax('apply',zssz,inputps);
[n,m]=size(zssz);
for k=1:1:m
x=inputn_test(:,k);
%计算输出中间层
for i=1:I
for j=1:M
u(i,j)=exp(-(x(i)-c(j,i))^2/b(j,i));
end
end
for i=1:M
w(i)=u(1,i)*u(2,i)*u(3,i)*u(4,i)*u(5,i)*u(6,i);
end
addw=0;
for i=1:M
addw=addw+w(i);
end
for i=1:M
yi(i)=p0_1(i)+p1_1(i)*x(1)+p2_1(i)*x(2)+p3_1(i)*x(3)+p4_1(i)*x(4)+p5_1(i)*x(5)+p6_1(i)*x(6);
end
addyw=0;
for i=1:M
addyw=addyw+yi(i)*w(i);
end
%计算输出
szzb(k)=addyw/addw;
end
szzbz3=mapminmax('reverse',szzb,outputps);
for i=1:m
if szzbz3(i)<=1.5
szpj3(i)=1;
elseif szzbz3(i)>1.5&&szzbz3(i)<=2.5
szpj3(i)=2;
elseif szzbz3(i)>2.5&&szzbz3(i)<=3.5
szpj3(i)=3;
elseif szzbz3(i)>3.5&&szzbz3(i)<=4.5
szpj3(i)=4;
else
szpj3(i)=5;
end
end
figure(3)
plot(szzbz1,'o-r')
hold on
plot(szzbz2,'*-g')
hold on
plot(szzbz3,'*:b')
xlabel('时间','fontsize',12)
ylabel('预测水质','fontsize',12)
legend('红工水厂','高家花园水厂','大溪沟水厂')
3.2 结果分析
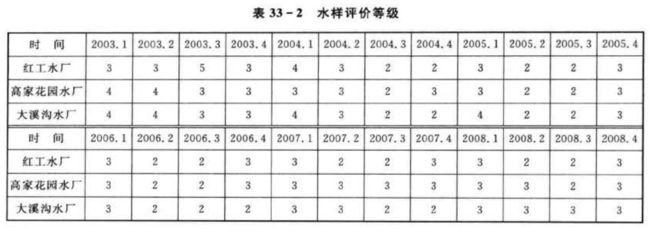
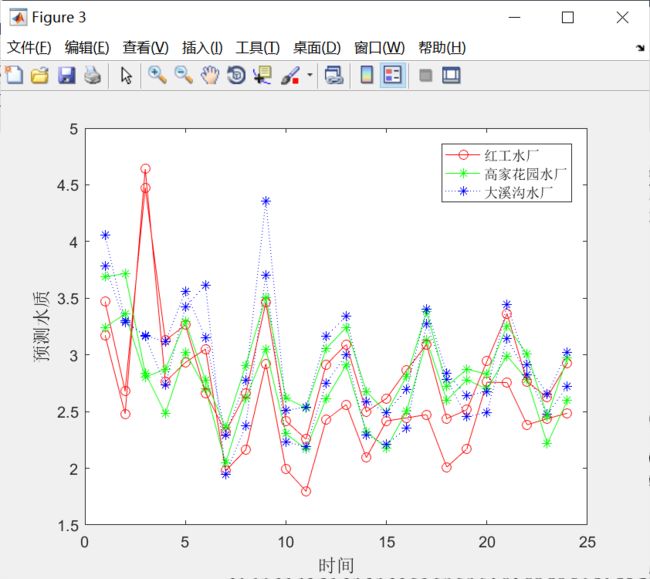
用训练好的模糊神经网络评价嘉陵江各取水口2003—2008年每季度采样水水质等级,网络评价结果如图33-8所示。各取水口水样评价等级如表33-2所列。
从水质评价等级可以看出嘉陵江上、中、下游三个取水口水样水质在2003—2004年间有一定改善,近几年变化不大,基本维持在2、3级左右。总体来说,上游水质评价结果优于下游水质评价结果,网络评价水质等级变化趋势同真实指标数据变化趋势相符,说明了模糊神经网络评价的有效性。
4.案例扩展
模糊神经网络是按照模糊系统原理建立的,网络中各个节点及其参数均有特定的物理含义,在网络初始化的时候,这些参数的初始值可以根据系统的模糊或定性的知识来确定,这样网络能够很快收敛。在本案例中,由于训练数据由《地表水评价标准》均匀线性内插得到,并且根据表达式可以看到,输入数据对网络输出的影响都是相同的,所以系数P的初始值都相同,隶属度函数b、c随机初始化得到。
5.完整代码和数据文件
完整代码和数据文件可以从这里下载:
基于模糊神经网络的嘉陵江水质评价Matlab代码