【局部活动轮廓】使用水平集方法实现局部活动轮廓方法研究(Matlab代码实现)
欢迎来到本博客❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
本文目录如下:
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码实现
1 概述
本代码实现参考了以下三篇文章。
[1] S. Lankton and A.Tannenbaum.'Localizing Region-Based Active Contours'. IEEE Trans on Image Proceesing 2008.
[2] A Yezzi Jr, A Tsai, A Willsky. A statistical approach to snakes for bimodal and trimodal imagery",IEEE ICCV 1999.
[3] Chan, T. F., & Vese, L. A. Active contours without edges. IEEE Transactions on Image Processing, 2001.
使用[1]设定的框架,实现了Mean Separation模型[2]和Chan-Vese模型[3]的本地化版本。
[1] S. Lankton和A.Tannenbaum在2008年发表的文章《Localizing Region-Based Active Contours》。该研究提出了一种基于区域的主动轮廓局部化方法,为本文的实现框架提供了重要的参考。
[2] A Yezzi Jr, A Tsai, A Willsky在1999年的文章《A statistical approach to snakes for bimodal and trimodal imagery》。这篇文章介绍了一种基于统计方法的蛇算法,用于处理双模态和三模态图像。本文在实现Mean Separation模型时借鉴了该方法,并进行了本地化的改进。
[3] Chan, T. F., & Vese, L. A.在2001年发表的文章《Active contours without edges》。该研究提出了一种无边缘的主动轮廓方法,能够有效地处理图像中缺乏明显边缘的情况。本文在实现Chan-Vese模型时参考了该方法,并进行了相应的本地化调整。
基于[1]设定的框架,本文成功实现了Mean Separation模型和Chan-Vese模型的本地化版本。通过结合这些先前的研究成果,我们能够有效地处理各种图像,并获得准确的分割结果。这些模型的实现为图像处理领域的研究和应用提供了有力的工具和方法。未来的工作可以进一步优化和扩展这些模型,以适应更广泛的应用场景。
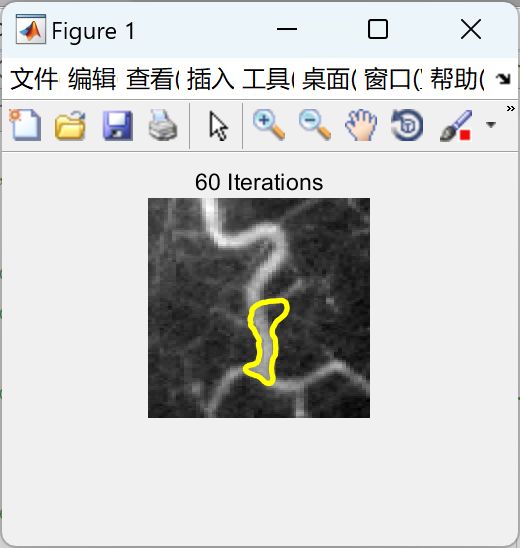
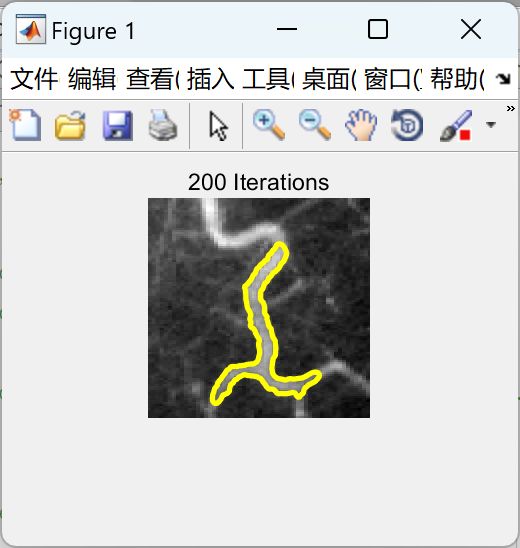
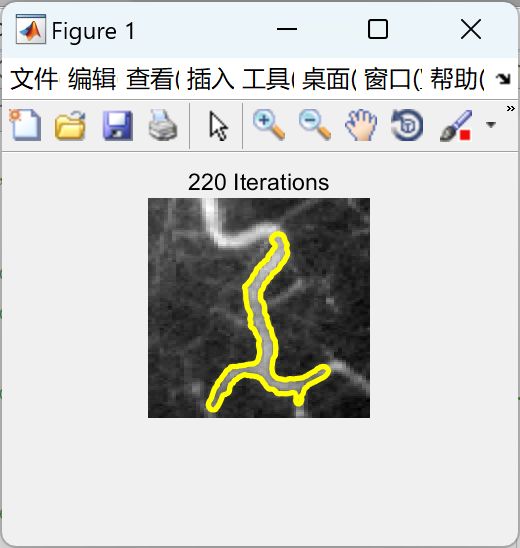
2 运行结果
部分代码:
function seg = local_AC_MS(Img,mask_init,rad,alpha,num_it,epsilon)
% This function aims to implement Shawn Lankton's local active contour. And
% the energy model is the MS model as defined in eq.(15)-(19).
% The local variables are calculated by filtering operation instead of
% iterating inspired by Chunming Li's IEEE TIP 2008 paper
%
% One small change is that I used a square window instead of disk for
% localization
%
% Input:
% 1. Img: image needs to be segmented
% 2. mask_init: intialization represented by binary image
% 3. rad: the side length of the square window
% 4. alpha: the coeficicent to balance the image fidality term and the
% curvature regularization term
% 5. num_it: maximum number of iterations
% 6. epsilon: epsilon used for delta and heaviside function
% Created by Jincheng Pang, Tufts University @11/09/2012
phi0 = mask2phi(mask_init);
phi = phi0;
B0 = ones(2*rad+1,2*rad+1);
% B0 = fspecial('disk',rad);
KI=conv2(Img,B0,'same');
KONE=conv2(ones(size(Img)),B0,'same');
for ii = 1:num_it
mask = Heaviside2(phi,epsilon);
I=Img.*mask;
temp1=conv2(mask,B0,'same');
temp2=conv2(I,B0,'same');
c1=temp2./(temp1); % local mean value inside
c2=(KI-temp2)./(KONE-temp1); % local mean value outside
A1 = temp1;
A2 = conv2(1-mask,B0,'same');
%%%%%
D = (A1.*A2+eps);
term1 = (A2-A1)./D;
term2 = (A2.*c1.^2-A1.*c2.^2)./D;
term3 = (A2.*c1-A1.*c2)./D;
dataForce = conv2(term1.*Dirac2(phi,epsilon),B0,'same').*Img.*Img + conv2(term2.*Dirac2(phi,epsilon),B0,'same')-2.*Img.*conv2(term3.*Dirac2(phi,epsilon),B0,'same'); %%% During the implementation, Img should be separated out of the filtering operation!!!
% dataForce = conv2(term1.*Dirac2(phi,epsilon).*Img.^2,B0,'same') + conv2(term2.*Dirac2(phi,epsilon),B0,'same')-2.*conv2(term3.*Dirac2(phi,epsilon).*Img,B0,'same');
dataForce = dataForce/max(abs(dataForce(:)));
% % curvature = get_curvature1(phi);
curvature = curvature_central(phi);
dphi = Dirac2(phi,epsilon).*(-dataForce + alpha*curvature);
dt = .48/(max(abs(dphi(:)))+eps);
%-- evolve the curve
phi = phi + dt.*dphi;
%-- Keep SDF smooth
phi = sussman(phi, .5);
if(mod(ii,10) == 0)
showCurveAndPhi(Img,phi,ii);
end
end
seg = (phi>=0);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%Auxiliary functions %%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%-- level set re-initialization by the sussman method
function D = sussman(D, dt)
% forward/backward differences
a = D - shiftR(D); % backward
b = shiftL(D) - D; % forward
c = D - shiftD(D); % backward
d = shiftU(D) - D; % forward
3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1] S. Lankton and A.Tannenbaum.'Localizing Region-Based Active Contours'. IEEE Trans on Image Proceesing 2008.
[2] A Yezzi Jr, A Tsai, A Willsky. A statistical approach to snakes for bimodal and trimodal imagery",IEEE ICCV 1999.
[3] Chan, T. F., & Vese, L. A. Active contours without edges. IEEE Transactions on Image Processing, 2001.