Ten simple rules for the computational modeling of behavioral data — 认知科学建模教程

原论文链接

Ten simple rules for the computational modeling of behavioral data

Abstract

行为数据的计算建模通过模型拟合实验数据，可以探索行为背后的算法，找到计算变量的神经关联，并准确地理解药物、疾病和干预措施造成的影响。但是伴随着强大的能力而来的是巨大的责任。此教程旨在提出一些计算建模的简单规则，以确保小心地、正确地使用计算建模。

What is the computational modeling of behavioral data

**目标：**使用准确的数学模型来更好地理解行为数据。

**行为数据的形式：**行为数据通常以选择的形式出现，但也可以是反应时间、眼动或其他容易观察到的行为。

**模型的形式：**模型以数学方程的形式出现，将实验中观察到的变量（如刺激、结果、过去的经验）与近期的行为联系起来。即以某些行为变量解释另一个或另一些行为是如何产生的。

计算模型实例化了关于行为如何产生的不同“算法假设”。

究竟什么是有意义的行为数据，在某种程度上是一个关于研究者的个人“爱好问题”，即由研究者的研究目的以及对研究问题的理解决定。正如机器学习领域广为流传的一句话所说：数据和特征决定了机器学习的上限，而模型和算法只是在逼近这个上限而已。所以，在某些情况下，基于对问题的理解所选出的具有代表性的解释变量在简单模型上的表现可能比盲目使用大而复杂的模型效果更好。

在某些情况下，一个能够解释数据的广泛定性特征的简单模型就足够了。而在其他情况下，需要更详细的模型来进行定量预测。针对不同的任务，制定不同的建模策略。

在文献中出现最多的计算建模的用途为：

1. 模拟 simulation

   通过设置特定参数的模型产生“假”的行为数据，然后用分析真实数据的方式来分析这些模拟数据。对数据中的定性和定量模式做出精确的、可证实的预测。模拟是一种使理论预测更加精确和可检验的方法。

2. 参数估计 parameters estimation

   对参数进行调整从而使得模型更好地解释真实行为数据，是一种拟合的过程。

3. 模型比较 model comparison

   探究一组模型中哪一个最能描述行为数据，以此来了解哪些机制是行为的基础。当不同的模型做出类似的定性预测，但在数量上有所不同时，这一点尤其有用。

   当竞争模型做出类似的定性预测时，说明这一机制能够较好地解释行为数据。

4. 潜变量推理 latent variable inference

   潜变量是不能被直接观察到，但是对系统的状态和能观察到的输出存在影响的一种变量。

   潜变量是无法直接衡量的变量。但是将这些潜在变量与其他可观察变量联系起来，可以从可观察变量的测量值推断出潜在变量的值。

以上四种使用方式每一种都有各自的强项和弱点，每一种方式都可能被错误的使用。这篇文章旨在提出一个友好的、完备的、实用的和面向细节的建模流程介绍，以避免初学者在建模中可能出现的错误。

这篇教程重点放在如何弄清楚一个模型告诉了我们关于**心智(mind)**的哪些信息。

1 Design a good experiment

计算建模是一种强大的技术，但它永远无法取代良好的实验设计

模型受到行为数据的影响，而行为数据又受到实验方案设计的影响。因此，建立一个好的模型的根本在于设计一个合理的实验方案。

作者举了两个例子：

1. 一个研究感知的研究者不会试图将强化学习模型用于感知决策任务
2. 一个研究收益和损失的不同影响的研究者也不会在一个必定有收益的赌博任务中进行研究

作者建议通过问自己以下几个问题来优化实验设计：

​ processes == 过程？

1. What scientific question are you asking? 你在询问什么科学问题？

   不要被实验设计所吸引而忘记想要达成的目标的最基本问题

   你的目标是什么认知过程？你想描述行为的哪个方面？你想挑出哪些假设？

   在设计任务时牢记研究目标，可以在以后节省很多时间。

2. Does your experiment engage the targeted processes?

   你的实验是否涉及目标过程？

   需要专家的知识和指导

3. Will signatures of the targeted processes be evident from simple statistics of the data?

   目标过程的特征能否从数据的简单统计中显现出来？

   作者举例：

   如果你正在研究工作记忆对学习的贡献，可以通过构建一个改变负荷的实验设计来寻找行为上的负荷特征，以增加探索工作记忆在学习中的作用的机会。

   在作者的经验中，如果在独立于模型的行为分析中没有证据显示效果，那么计算模型就不太能提供有效的信息。（不对模型进行优化，简单地改变某个参数，观察模型是否有所改变）

要回答这些问题，重要的是要有一个明确的理论假设，说明要对什么现象进行建模。设计一个好的实验与设计一个好的模型是相辅相成的，而且这两个步骤应该同时进行

作者举了一个例子：多臂老虎机问题

参与者在 K 个老虎机（或称"独臂强盗"）之间做一系列 T 个选择，试图使收益最大化。在第 t 次试验中，每台老虎机 k 都会有${\mu }_t^k$的概率得到奖励 $r_t$ ，不同老虎机的奖励是不同的，而且最初对被试者来说是未知的。在该问题的简单版本中，获得奖励的概率在一段时间内是固定的。

这个任务的三个实验参数是：试验次数T，老虎机数量K，以及不同老虎机的的奖励概率${\mu }_t^k$。在这个例子中假设T = 1000，K = 2，老虎机1的奖励概率为${\mu }_t^1$ = 0.2，老虎机2的奖励概率为${\mu }_t^2$ = 0.8。这些参数可能会也可能不会随着时间变化。这些参数的设置对于确定我们到底能从实验中提取什么信息非常重要（参数的不同会影响模型做出的选择）。

2 Design good models

就像糟糕的实验会限制我们测试不同假设的能力一样，糟糕的模型—相当程度上是我们假设的数学体现—会进一步限制我们得出的结论。

在设计新的模型时，这一点尤其重要，但即使是成熟的计算模型在某些情况下也会有问题。

不同的设计模型的方法：

1. 启发式方法寻找处理信息的“合理方式”以产生目标行为（delta规则）

2. 在人工智能、计算机科学和应用数学文献中搜寻已经用于解决类似问题的智能体(artificial agents)算法

   这种方法在强化学习领域得到了卓有成效的应用。Q-learning和时间差分算法已经和人类和动物的行为和大脑功能产生了联系

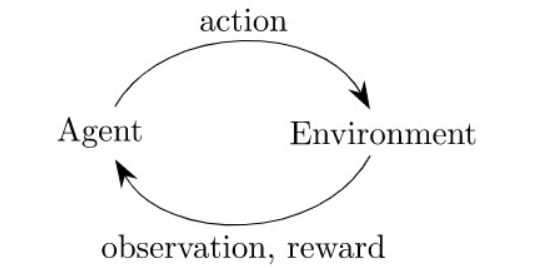
   Environment-Agent框架是强化学习系统的一个框架

   

   智能体通过一些策略输出一个行为(Action)到环境，环境反馈状态值(Observation)和奖励值(Reward)到智能体，同时环境会转移到下一个状态，智能体根据环境反馈的奖励做出下一步的选择。如此不断循环，最终找到一个最优的策略。

3. 采取贝叶斯最优化的观点，设计出在特定环境和任务下的模型表现最优的算法。

   一个成功应用的例子是视觉领域的理想观察者模型。

   贝叶斯最优模型可以通过研究近似于理想策略的更简单的算法，或者通过对理想观察者智能体施加有界性约束，如有限的计算资源，来进一步追求贝叶斯最优模型

无论采用什么方法设计模型，重要的是记住以下几点：

1. 一个计算模型应当尽可能的简单（简单的模型具有更好的可解释性）

   只要能够解释数据，倾向于选择更简单的模型

   模型比较技术包括对于过于复杂的模型的惩罚（正则化等），复杂的模型更容易过拟合且泛化性差。

2. 一个计算模型应当尽可能做到是可解释的

   无法解释的模型有可能会提高拟合度，但无意义的参数值可能表明模型中缺少一些重要的东西，或者完全是一个不同的认知过程在起作用（因为无法解释到底是什么起了作用）

3. 模型应当可以捕获你计划测试的所有假设

   尽管设计能够表达你的主要假设的模型很重要，但是设计出能捕获竞争性假设的模型更重要。

   应当在拟合这些模型（一方面是支持自己的假设的模型，另一方面是与自己的假设存在矛盾的模型）上付出相同的努力，让数据来决定哪个模型是最合适的，而不是自己的主观臆断。

作者举例：多臂老虎机的行为建模

设计了参与者可能在多臂老虎机任务中可能的表现的五种模型

模型1：随机响应模型

假设参与者不参与任务，只是随机地按下按钮。

这种随机行为在行为实验中并不少见，特别是当参与者没有外部激励来获得良好的表现的时候。

假设参与者在两个选项中随机选择，用 b 表示选择其中一个选项的概率，则这两个选项的概率为：
$$p_t^1=band{p}_t^2=1-b$$
因此，对于两台老虎机的问题，随即响应模型只有一个参数 ${\theta }_1=b$

模型2：有噪音的赢-留-输-变模型

赢-留-输-变模型是最简单的模型之一，它根据反馈来调整自己的行为。在该模型的噪音版本中，以概率方式应用该规则。

假设该模型以$1-ϵ$的概率应用赢-留-输-变策略，以$ϵ$的概率随机选择。在第 t 次决策中，选择第 k 个老虎机的概率为：
$$p_t^k=\{\begin{array}{ll}1-ϵ/2& if(c_{t-1}=kand{r}_{t-1}=1)OR(c_{t-1}\ne kand{r}_{t-1}=0)\\ ϵ/2& if(c_{t-1}\ne kand{r}_{t-1}=1)OR(c_{t-1}=kand{r}_{t-1}=0)\end{array}k\in \{1,2\}$$
其中 $c_t=1,2$为第 t 次实验的选择，$r_t=0,1$是第 t 次实验的奖励。该模型也只有一个参数 ${\theta }_2=ϵ$

模型3：Rescorla-Wagner模型

在该模型中，参与者首先根据以前的结果历史来计算每个老虎机的期望奖励，然后利用这些值决定下一步该采取怎样的策略。在Rescola-Wagner模型中选项 k 的奖励预期值$Q_t^k$由$r_t$根据以下规则更新：
$$Q_{t+1}^k=Q_t^k+\alpha (r_t-Q_t^k)$$
其中$\alpha$ 是学习率，取值为[0,1]，反应了预测误差$r_t-Q_t^k$的更新程度。$Q_0^k$初始预期，可以看作模型的自由参数，为了简单起见，假设$Q_0^k=0$。

一种被称为“softmax” 的选择方法选择选项 k 的概率为：
$$p_t^k=\frac{exp(\beta Q_t^k)}{{\sum }_{i=1}^{K}exp(\beta Q_t^i)}$$
其中 $\beta$ 逆温度参数，控制选择中的随机性水平，$\beta =0$表示完全随机响应，$\beta =\infty$表示一定选择奖励值最高的选项。将学习方式(公式 3) 和决策规则(公式 4)结合起来，就得到了具有两个自由参数$\beta \alpha$ 的简单决策模型。模型的参数${\theta }_3=(\alpha ,\beta )$。

模型4：选择核模型

选择核模型试图捕获人们重复之前行为的趋势。假设参与者为每个行为计算一个选择核：
$$C{K}_{t+1}^k=C{K}_t^k+{\alpha }_c(a_t^k-C{K}_t^k)$$
其中，当选项 k 在第 t 次实验中被选择时$a_t^k=1$，否则$a_t^k=0$。${\alpha }_c$是选择核的学习率，当${\alpha }_c=1$时，这个模型与模型2 赢-留-输-变模型非常相似。

选择核的更新方式与Rescorla-Wagner模型的规则基本相同：
$$p_t^k=\frac{exp({\beta }_{c}C{K}_t^k)}{{\sum }_{i=1}^{K}exp({\beta }_{c}C{K}_t^i)}$$
将选择核(公式 5)和决策规则(公式 6)结合起来可以得到一个简单的决策模型，该模型由两个自由参数：选择核学习率${\alpha }_c$和逆温度参数${\beta }_c$，${\theta }_4=({\alpha }_c,{\beta }_c)$

模型5：Rescorla Wagner + 选择核模型

最复杂的模型混合了Rescorla Wagner这一强化学习模型和选择核模型。

选项 k 的奖励期望值根据公式 3 更新，选择核根据公式 5 更新。

这些公式结合起来后得到如下的概率表达式：
$$p_t^k=\frac{exp(\beta Q_t^k+{\beta }_{c}C{K}_t^k)}{{\sum }_{i=1}^{K}exp(\beta Q_t^i+{\beta }_{c}C{K}_t^i)}$$
这个模型有四个自由参数 ${\theta }_5=(\alpha ,\beta ,{\alpha }_c,{\beta }_c)$

3 Simulate, simulate, simulate!

在设计实验和选择模型后，非常重要的一个步骤就是生成假数据，或替代数据。然后用模型来模拟实验中参与者的行为，并观察不同的模型、不同的模型参数和不同的变体的行为变化。这一步骤可以改进前两个步骤：确认实验设计引发了假定由计算模型可以捕获的行为。

为了做到这一点，作者给出了以下重要步骤：

1. 定义独立于模型的衡量标准

   找到模型的定性特征(通常不止一个)是至关重要的。用与模型无关的措施来分析真实行为。

2. 在参数值范围内对模型进行模拟

   将行为视为参数的函数，了解模型的自由参数是如何影响行为的。

   

   上图显示了对模型3 Rescorla-Wagner的参数空间的探索，绘制了前十次试验和后十次试验中选择正确的概率p(correct)与学习率$\alpha$和softmax的参数$\beta$的关系

3. 可视化不同模型的模拟行为

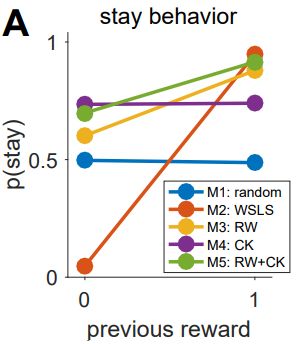
   这可以验证不同模型的不同行为使它们在实验中的预测不同。如果不同模型的行为没有质的不同，说明应该尝试设计一个更好的实验。

   根据模型在数据上的定性模式区分模型总是比定量模式更可取。

   

   例如CK选择核模型和random随机响应模型，虽然在同一previous reward下重复一个动作的概率不同，但是随着previous reward的增加，这两个模型重复上一次选择的概率趋势是相同的。RW+CK和RW模型也是如此。

模拟过程的目标是阐明模型和实验设计如何满足你的目标，即识别行为中的认知过程。如果实验的内容足够丰富，可以捕捉到预期的行为，模型的参数是可以解释的，而且竞争模型可以做出没有关联的预测，就可以进入下一个步骤。否则，应当回过头来看前三个步骤出现了哪些问题。这是第四步，拟合参数的先决条件。

4 Fit the parameters

计算建模的一个关键部分是估计最能描述你的行为数据的参数。作者在这里以极大似然估计法举例。

**目标：**在参数$p(d_{1:T}|{\theta }_m,m)$给定的条件下，找到模型的参数$m、{\hat{\theta }}_m^{MLE}$ 使得数据$d_{1:T}$似然值最大化。一般以最大似然值的对数来替代最大似然值 $LL=logp(d_{1:T}|{\theta }_m,m)$，将连乘替换成连加，可以避免精度问题。

$LL$可以用单个模型的选择概率来表示：
$$LL=\log p(d_{1:T}|{\theta }_m,m)=\sum _{t=1}^T\log p(c_t|d_{1:t-1},s_t,{\theta }_m,m)$$
最简单的寻找函数的极值的方法是搜寻整个参数空间，但是这种方法时间复杂度很高。另外一些方法利用梯度上升或梯度下降算法快速找到函数的局部最大值或最小值，例如matlab中的fmincon函数（神经网络中的梯度下降法）。

在试图最大化$LL$的过程中可能会遇到一些问题，作者给出了以下建议：

1. 确保在初始化条件下，对数函数的值是有限的

   像fmincon这样的优化器要求指定初始参数值，如果这些初始参数对应的似然估计值可能不是计算机能够表示出的数字(例如无穷大或者NaN)。这可能是拟合失败的原因之一。

2. 小心四舍五入错误、零和无穷大

   如果在参数搜索过程中遇到无穷大或NaN（爆精度，将似然值加上log就是为了避免这种情况的发生），拟合过程就会出现错误。例如，一个选择概率被四舍五入为0，那么概率的对数就为$-\infty$。如果模型涉及指数（比如softmax），那么也可能导致一个比较大的数字经过指数运算后被视为无穷大。

   避免这些问题的方法之一是约束参数值的取值范围，使其在取值范围边界时也可以得出有意义的、有限制的概率值或似然估计值。

3. 谨慎对待参数的约束条件

   如果约束条件选择不当，可能最小值(最大值)会在参数的约束范围外。（Grid Search网格搜索时，最佳参数组合可能不在设定的范围内）

4. 只考虑对似然值有影响的参数

   如果只有两个参数对似然值有影响，但是优化器试图拟合三个参数，这将导致拟合速度变慢、效率变低

5. 小心局部最小值

   像fmincon这样的优化器只能保证找到局部最小值，而无法保证找到的是全局最小值。（Adam、momentum、RMSProp、SGD）

   一种解决方法是，使用随机初始化条件多次运行拟合过程，似然值最大的那次拟合过程对应的参数为最佳参数。随着拟合次数的增加，最佳拟合似然值将逐渐接近函数的真实最大似然值。

作者举了一个具有局部最大值的例子：

一个混合强化学习的工作记忆模型，这个模型有两个参数 $\rho$ 工作记忆的效果；$\alpha$ 强化学习的学习率。

如下图所示，参数空间对应多个局部最大值。从起点开始，优化器可以收敛到这些局部最大值中的任何一个。解决方法就是选择不同的起点，多次重复运行拟合程序，选择最大似然估计值对应的初始参数作为最优参数。

图中红色的 × 表示生成参数(generative parameters)；黑色的圆圈表示使用暴力搜索法找到的最优参数；黑色 * 表示用fmincon和多个起点找到的最优参数。

如右图所示，随着起点数量的增加，拟合得最好的似然函数值和参数将收敛到全局最大值。

随着起点数量的增加，如果最佳拟合参数与全局最佳拟合参数的距离值看起来已经变成了一条渐近线，说明很可能已经做到了最好的拟合。

5 Check you can recover your parameters

参数恢复：检查拟合程序是否在拟合由真实参数值模拟出的假数据时给出了有意义的参数值。

参数恢复的过程:

1. 用已知参数模拟生成假数据
2. 用模型对生成的假数据进行拟合
3. 将恢复的参数与它们的真实值进行比较

在理想状态下，模拟的参数和恢复的参数应当是紧密相关的，不存在偏差。如果模拟参数和恢复参数之间没有很强的相关性或出现明显的偏差，这表明程序中存在错误，或者设计的实验不足以评估此模型。

作者给出以下建议：

1. 确保模拟参数在正确范围内

   一些模型/实验只有在特定范围内的参数才能得到良好的参数恢复，如果模拟参数过大或过小，就难以恢复。比如softmax的参数$\beta$，大于一定值的$\beta$在实验中会导致几乎相同的行为。因此，对于大的$\beta$值来说，参数恢复可能会失败，但是对于较小的$\beta$来说，参数恢复的效果较好。

   • 如果已经拟合了数据，将模拟参数的数据与拟合得到的数值范围相匹配
   • 如果还没有拟合数据，但是使用的是其他作者已经发表的模型，将参数范围与研究中的范围相匹配
   • 如果是新模型，“真正的”、最合适的参数是未知的，那么在尽可能大的范围内进行搜索，以了解参数是否可以恢复，以及在哪里可以恢复。

2. 绘制模拟参数和恢复参数的相关系数

   

3. 确保恢复过程不会引入参数之间的相关性

   除了观察模拟参数和恢复参数之间的相关性之外，作者还建议观察恢复参数本身的相关性。如果模拟参数之间是不相关的，那么恢复参数之间的相关性就表明模型中的参数正在互相交换。

4. 关于不同人群或条件之间的参数差异的说明

   模型拟合的一个越来越多的用途是比较不同人群（比如精神分裂症患者和健康对照组）或不同情况下的参数值。参数恢复可以用来给出模型统计能力的估计。

5. 即使得到了一个最好情况下的参数恢复，也要记住：

   成功的参数恢复是：由一个具有给定参数的已知模型产生的数据可以被拟合以恢复这些参数。

   而这种成功的参数恢复是不太可能发生的，因为行为的“真正”生成过程—即思想和大脑的内部运作比你能想到的任何模型都复杂。所以，在展示成果的时候记得保持谦虚。

作者用模型 3 (Rescorla Wagner 模型)对双臂老虎机任务进行了参数恢复：

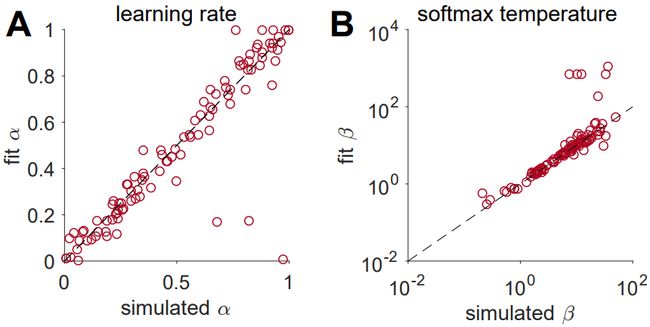
根据公式 3 和公式 4 模拟模型的动作；然后根据模型模拟出的动作，用最大似然估计法拟合参数，得到拟合出的学习率$\alpha$和softmax的参数$\beta$

从图中可以看出，模拟值和拟合值具有相当好的一致性。$\beta$在 (0.1,10)范围内拟合得最好，在这个范围之外就不那么好。

使用从拟合真实数据得到的参数范围来检测参数的恢复质量可能是一个更好的选择。

6 Can you arbitrate between different models?

在模型比较中，我们的目标是确定一组可能的模型中最有可能生成某种数据的模型。

一个简单的比较方法是比较每个模型在最佳拟合参数设置下的对数似然值，即$p(d_{1:T}|{\hat{\theta }}_m,m)$。

但是，如果用于评估对数似然函数的数据$d_{1:T}$与用于拟合参数的数据相同，那么这种方法将导致过拟合。（在训练集上测试）。

过拟合问题会降低模型的可推广性(泛化性)，为了避免过拟合问题，需要考虑模型中的自由度。可采用的方法有：对自由参数的惩罚和在非样本数据(测试集)上测试拟合度。

作者在本教程中讨论一种简单的方法—贝叶斯信息准则 BIC，它对自由参数有一个明确的惩罚：
$$BIC=-2log\widehat{LL}+k_m\log (T)$$
其中，$\widehat{LL}$是最佳拟合参数设置下的对数似然值，$k_m$是模型$m$中的参数个数。BIC得分最小的模型是最适合数据的模型，因此，方程中的后一项$k_m\log (T)$对应于对参数数量多的模型的惩罚。

BIC 是一种简单的寻找适合你的数据的方法，但是为了确保模型的比较有意义，还需要一些额外的步骤：

1. 用模拟数据来验证模型的比较

   正如参数拟合应该通过模拟数据的参数恢复来验证一样，模型比较也应该通过模拟数据的模型恢复来验证。

   这个过程包括模拟出所有模型的数据，然后用所有模型拟合所有这些数据，以确定模型 A 产生的模拟数据在多大程度上由模型 A 而不是由模型 B更好地拟合。这个过程可以被表达成一个混淆矩阵，量化每个模型有多大的概率能够最好地拟合别的模型产生的数据。

   在理想情况下，混淆矩阵是一个单位矩阵，但在实践中并不总是如此。

2. 使用不同的模型比较方法

   如果混淆矩阵有很大的非对角线成分，那么说明模型恢复可能存在问题。

   有许多因素可能导致这个问题，比如代码错误、实验设计不足等。是否使用了错误的方法惩罚参数也是一个值得考虑的问题。

   不同的参数惩罚措施在不同的假设下以不同的方式惩罚参数，如果混淆矩阵不是单位矩阵，可能是参数惩罚方法(比如 BIC)所依据的假设对你的模型不成立。可以尝试其他的模型比较指标，比如 AIC。

3. 模型比较中明显存在的问题

   模型比较的一个问题是，它只告诉你在你所考虑的模型中，最能拟合行为数据的模型是哪个。但是还有无穷无尽的模型没有被考虑。所以在设计模型时就需要尽可能地找到一组好的模型。

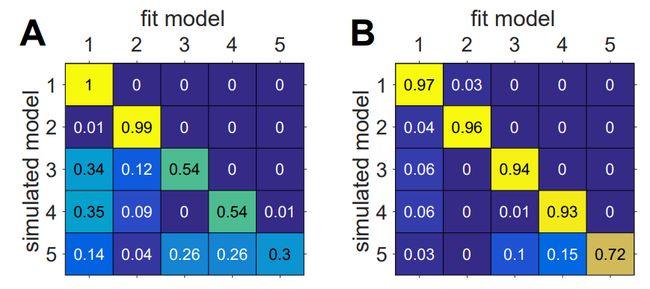
举例：双臂老虎机任务中的混淆矩阵

作者模拟了五个模型在双臂老虎机任务中的行为，计算出混淆矩阵

图A的混淆矩阵，参数是在以下范围内随机取样的

图B的混淆矩阵，softmax的参数$\beta$和${\beta }_c$都增加了1，减少了行为数据中的噪音量，使得模型更容易识别，对应的混淆矩阵更类似单位矩阵。

混淆矩阵如此依赖于模拟参数的值意味着，尽可能使模拟参数与实际拟合出的参数相匹配是比较重要的。在一个参数体系中可以相互区分的一组模型，在另一个参数体系中可能无法相互区分。

7 Run the experiment and analyze the actual data

在完成以上步骤后，就可以开始对真实的观察数据进行建模。

在建模之前，需要对数据进行分析，这一步是非常重要的。如果独立于模型的分析没有显示出预期结果的证据，那么拟合模型就几乎没有意义。

作者的经验是：如果没有独立于模型的证据表明想要研究的认知过程能够通过行为数据体现，那么基于模型的分析就不可能发现这些认知过程存在的证据

如果独立于模型的数据分析得到了比较好的结果，那么下一步就是拟合之前开发的模型并进行模型的比较。

用真实数据对模型进行拟合后，应该比较拟合得到的参数范围是否与参数恢复和模型恢复步骤中得到的参数范围相匹配。如果超出了后者的范围，那么应该回到参数恢复和模型恢复的步骤中去，使得这两个步骤得到的参数范围与经验参数范围相匹配，从而确保模型拟合和模型比较步骤得到可解释的结果。

需要记住的是，人类行为总是比模型更加混乱，我们探索的那些模型不太可能真正包含能够捕捉人类行为的模型。

所以，应当循环考虑步骤 2-5（设计模型、生成模拟数据、拟合参数、参数恢复），在对数据的独立于模型的分析的指导下，改进模型。例如，可以考虑对不重要的—对你的科学问题无关的参数进行建模，通常可以捕获到行为中可能被视为噪声的变化。因此，可以更好地估计“重要”参数。例如，在决策或学习任务中，通过避免将预先存在的偏好（比如对左/右选择的偏好）看作噪声，可以对逆温度更好的估计，从而为其他参数如学习率提供了更好地估计。

举例：通过对不重要的参数进行建模来提高参数恢复能力

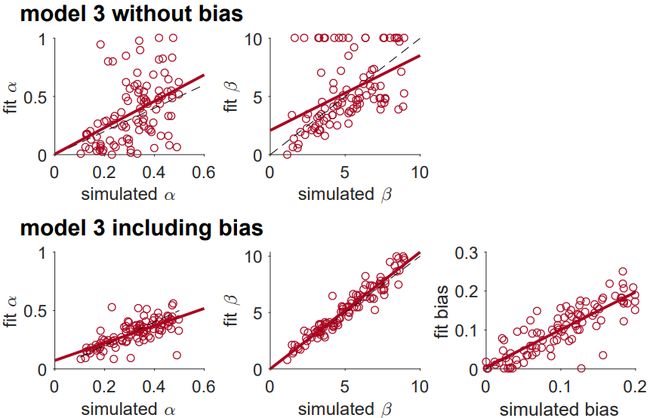
为了说明不重要的参数对拟合结果的影响，作者在模型3 (Rescorla-Wagner模型)模拟了侧偏见(side bias)对参数恢复的影响。假设除了学习率外，模型还有一个侧偏见参数 B，它可以改变选择左边老虎机的概率。双臂老虎机问题的选择概率变成：
$$p_t^{left}=\frac{1}{1+exp(\beta (Q_t^{right}-Q_t^{left}-B))}$$
（根据Rescorla-Wagner模型的公式，分子分母同时除以$Q_t^{left}$得到上式）

另一点改变是，奖励每50次实验在$\mu =\{0.2,0.8\}$和$\mu =\{0.8,0.2\}$之间切换。

如下图所示，将“不重要的”偏差纳入拟合过程，大大改善了学习率$\alpha$和softmax参数$\beta$的恢复程度。

8 Validate(at least) the winning model

所有前面的步骤都是在比较相对的拟合度，即模型 A 是否比模型 B 更合适。但是，在解释一个模型的结果之前，必须保证该模型在绝对意义上有效地捕捉了数据背后的行为。这个步骤被称为模型验证，并且这个步骤永远不应该被跳过。否则会导致：得到了一个高拟合度的模型，但是完全忽略了行为数据的本质。

模型验证的一种方法是计算所有试验的平均似然值，这是一种衡量拟合效果的绝对措施。例如，当模型完全预测了行为时，最好的似然值可能是1，但是当选择是完全随机的或环境比较复杂时，可能反应的衡量价值不大。在这种情况下，每次实验的最佳似然值可能小于1。基于此，虽然每次试验的似然值可能是一个验证模型的有用工具，但价值有限。

验证模型的更好的方法是用拟合得到的参数值进行模拟（生成由模型模拟的行为数据）。然后，以分析真实数据的方式分析模拟数据，以验证所有重要行为效应是否被模型通过拟合参数的模拟所定性或定量地捕获。

Palminteri等人的工作提供了这样一个例子：通过任何量化措施对模型进行比较，模型 A 都比模型 B 拟合得要好，但是模型 A 完全无法捕获到行为的本质。

模型 A ，选择核模型，倾向于重复之前做出的选择

模型 B，赢-留-输-变模型，只取决于上一次的选择

数据是由一个强化学习智能体在反转学习任务中产生的。

由于强化学习智能体所作选择的自相关性，倾向于重复之前行为的模型A比模型B的表现更好。但是模型 A 对奖励完全不敏感，因此在用拟合的模型参数进行模拟时，完全无法产生反转行为。

这个例子说明了选择核策略的重要性：如果产生选择的策略不对，模拟数据会比模型比较更好地揭示这一点。

9 Estimate latent variables

基于模型分析的一个特别强大的应用是估计模型中的潜变量。潜变量是行为背后的算法的隐藏部分，它不能从行为本身观察到，但是这些潜变量揭示了模型内部是如何运作的。

一旦潜变量被估计出来，就可以和其他可观察的变量一样用于数据分析。可以和生理学数据相结合，如瞳孔放大、EEG脑电图、FMRI功能性磁共振成像。这些方法中最简单的是使用线性回归来测试生理变量是否与注意的潜变量相关，这种方法引导出了对行为背后的神经机制的一些理解。

10 Reporting model-based analyses

在这一节中作者介绍了实验完成后，在论文中应该书写的内容。

10.1 model selection

1. 模型恢复分析：混淆矩阵

   需要证明你的分析/实验有能力在模拟数据的条件下区分不同的模型，可视化这些结果的最好方法就是使用混淆矩阵。

2. 每一个模型拟合得最好的受试者的数量

   最简单的方法是使用直方图显示每个模型拟合得最好的受试者的数量，以直观地体现最好的模型对数据的拟合程度。如果所有受试者都被一个模型拟合得最好，这是理想的情况，但是更有可能出现的情况是，一些受试者会被其他的模型拟合得更好，在论文中承认这样的结果是很重要的，因为这可能反映了不同的人使用了不同的选择策略，或者“正确”的模型（能够最好地拟合所有受试者数据的模型）在实验所考虑的模型之外。

3. 组层面的统计：超越概率

   报告模型比较结果的一个更复杂的方法是计算一个单一模型最好地描述所有数据（所有其他模型生成的模拟数据）的概率—超越概率。这些概率可以用直方图或者表格的形式报告。

4. 与模型无关的模拟数据的判定

   证明一个模型优越性的最彻底的办法是，该模型能解释其他模型所不能捕捉到的数据中的定性模式。

10.2 Parameter fits

在某些情况下，将参数与行为数据进行拟合是论文的重点，在其他情况下，参数拟合可能是模型比较的次要内容。但是在所有情况下，作者建议以尽可能透明的方式报告拟合参数值。

1. 报告参数值的分布

   报告参数拟合的最简单的方法是绘制所有拟合参数值的分布图，这可以让人对总体中每个参数的变化性有很强的感受，也可以说明拟合出现的问题。例如，如果大量的拟合参数集中在上界或下界附近，这可能说明模型存在问题。

2. 绘制拟合参数值之间的成对的相关性

   通过绘制参数见成对相关性的散点图，可以更深入地了解拟合参数之间的关系。与单个参数的直方图一样，这种方法提供了参数分布的直观感受，并可以提供模型存在问题的证据：例如，如果两个参数互相权衡，可能说明这些参数在这个实验中无法分辨开来。

3. 报告参数恢复

   所有的参数拟合分析应该建立在对模拟数据进行全面的参数恢复分析的基础上。如果在模拟数据的理想情况下不能恢复参数，那么这些参数就几乎不能告诉我们真实行为所反映的信息。

10.3 Share your data and code！

作者鼓励分享数据和代码。分享的数据应该是原始的实验数据，尽量不经过预处理操作。分享的代码应该能重现实验中的每一个步骤，以及生成论文中的所有图表。

10.4 Should you always report all of your modeling results？

如果你使用的是一个已经被提出的模型，那么跳过上述的很多步骤，只报告最后的结果；或者使用的是别人开发的代码，而并不理解代码究竟做了什么；走这种捷径是错误的。

首先，实验或人群可能是不同的，模型在这种情况下可能有不同的表现。另外，很多已经被提出的模型没有以系统的方式得到验证。与其他研究一样，当使用计算模型时，你需要证明你正在正确地应用这个方法，而不是直接给出结果。

总之，即使建立模型不是论文的中心点，也应该报告所有的建模结果。

11 What now？

一个建模者的工作永远不会完成。作者引用Geooge Box 的话说：没有正确地模型，只有有用的模型，还需要经过以下步骤的考虑，以检验模型是否真的描述了头脑中的一个过程。

1. 改进模型以解决与现有数据集的差异。

   模型拟合不会到到完美，即使在最好的情况下，也常常与实际数据有微小的差异，尝试改进模型来解决这些差异，例如考虑额外的参数，或者设计新的模型。

2. 使用模型做预测

   最好的模型不止能解释实验中的数据，还能够预测新情况下的数据。使用从新的实验中收集的，或者是其他研究的数据来调整模型使其具有普适性。