N圆最密堆积、最小外接正方形的matlab求解(二维、三维等圆Packing 问题)
圆形最密堆积、最小外接正方形的matlab求解(二维、三维等圆Packing 问题)
- 0 前言
- 1 N个圆的最小外接正方形求解
- 2 N个球的最小外接立方体求解
惯例声明:本人没有相关的工程应用经验,只是纯粹对相关算法感兴趣才写此博客。所以如果有错误,欢迎在评论区指正,不胜感激。本文主要关注于算法的实现,对于实际应用等问题本人没有任何经验,所以也不再涉及。
0 前言
本文最开始的想法,是想到一个我有若干个球,究竟需要多大的箱子可以把这些球装下。
后来大概查了一下资料,发现这其实是一个最优化的问题,而且似乎还非常复杂。对于圆来说,还有比较简单的优化方法,但是对于复杂图形来说,则非常困难。
自己也不是专门搞最优化的,就不编自己的函数了,直接用matlab现成的函数进行求解。下面举两个例子作为说明。
更好的例子可参见这篇2019年的论文:
王正理《等圆Packing问题高效求解算法研究》
20以下的最密堆积可以直接在wiki百科上查表得到,词条为:Circle packing in a square
10000以下的最密堆积可以在这个网站查到:
http://hydra.nat.uni-magdeburg.de/packing/csq/csq.html
1 N个圆的最小外接正方形求解
这个先用2维平面问题作为引入。
优化函数用的是fmincon()函数。
这里之前也试过PSO算法,但是估计维度太多,有些空穴小球移动完全不影响最终外接矩形,所以收敛速度异常的慢。经常出现某一些圆挤到一块,但某些圆离得很远。所以还是用传统的最优化方法。
目标优化函数,也就是让其最小的函数,就是正方形的变长。
边界大致设置了左右边界,防止圆离开边界太远。
非线性约束,就是计算每个圆之间的距离,防止发生重叠。
在计算过程中,最容易出现的现象就是圆和圆之间距离过大,就提前结束计算了,比如下面这个图:

为了让其收敛,需要手动的将各个圆之间的距离缩小。我这里用的方法比较简单,就是将所有坐标除以1.5或者其它大于1的数,让其整体向左下角压缩。通常在计算一定步骤之后,再进行压缩,然后继续计算,反复多次,可以让其收敛到较好的结果。
最终代码如下:
clear
clc
close all
%计算圆的最小外接矩形(任意数量N)
%利用fmincon算法
%求解函数最小值
N=13;%圆的数量
%设置optimoptions的输入
fun = @MinValue;
lb = -2*ones(1,N*2);%[xi,yi,xi,yi,...]
ub = (4*N-2)*ones(1,N*2);
A = [];
b = [];
Aeq = [];
beq = [];
%按照网格布置初始圆
NMesh=ceil(sqrt(N));
[XMesh,YMesh]=meshgrid(0:4:(4*NMesh-1),0:4:(4*NMesh-1));
XYMesh=[XMesh(:),YMesh(:)]';
x0=XYMesh(1:2*N);
x0=x0+rand(1,2*N)-0.5;%添加随机性
%非线性约束,目的是让圆和圆之间不重叠
nonlcon = @NolinearCondition;%设定非线性约束条件
options = optimoptions('fmincon','Display','iter','Algorithm','interior-point','MaxFunctionEvaluations',inf);
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options);
%放大圆形,然后再计算一次。相当于让圆膨胀一下,然后利用约束条件再迭代一下
x=x/1.2;
options = optimoptions('fmincon','Display','iter','Algorithm','sqp','MaxFunctionEvaluations',inf,'MaxIterations',1e5);
x = fmincon(fun,x,A,b,Aeq,beq,lb,ub,nonlcon,options);
%放大圆形,然后再计算一次。相当于让圆膨胀一下,然后利用约束条件再迭代一下
x=x/1.05;
x = fmincon(fun,x,A,b,Aeq,beq,lb,ub,nonlcon,options);
%绘图
figure()
hold on
for k=1:N
rectangle('Position',[x(2*k-1)-1,x(2*k)-1,2,2],'Curvature',1)
end
minX=min(x(1:2:end-1));
maxX=max(x(1:2:end-1));
minY=min(x(2:2:end));
maxY=max(x(2:2:end));
rectangle('Position',[minX-1,minY-1,maxX-minX+2,maxY-minY+2],'Curvature',0)
%非线性约束
function [c,ceq] = NolinearCondition(x)
%格式固定,c(x) ≤ 0 和 ceq(x) = 0。如果没有就是[]
N=length(x)/2;%点的数量
%转化坐标
xy=zeros(2,N);
xy(:)=x(:);
xy=xy';
%计算距离
DAll=pdist(xy,'squaredeuclidean');%距离的平方(这样省去了根号,加快计算速度)
%N个小球之间不碰撞,计算所有的负距离之和
DAll=DAll-4;
DNeg=sum(DAll(DAll<0));
%要让c<=0
c = -DNeg;%
ceq = [];
end
%评价函数
function V=MinValue(x)
%求包围两个圆的最小正方形边长
%x=[x1,y1,x2,y2,....]
%N=length(x)/2;%点的数量
%半径为1的圆
minX=min(x(1:2:end-1))-1;
maxX=max(x(1:2:end-1))+1;
minY=min(x(2:2:end))-1;
maxY=max(x(2:2:end))+1;
%计算正方形边长
L=max([maxX-minX,maxY-minY]);
V=L;
end
下面举几个最终结果,注意,这里只是给出了较优的解。因为小球数量越多,维度越大,几乎没有人能够说自己给出的解就是最优解。
N=9时的计算结果,显而易见,最密堆积就是3×3的形式。小球半径为1,正方形变长为6。

N=13的情况:
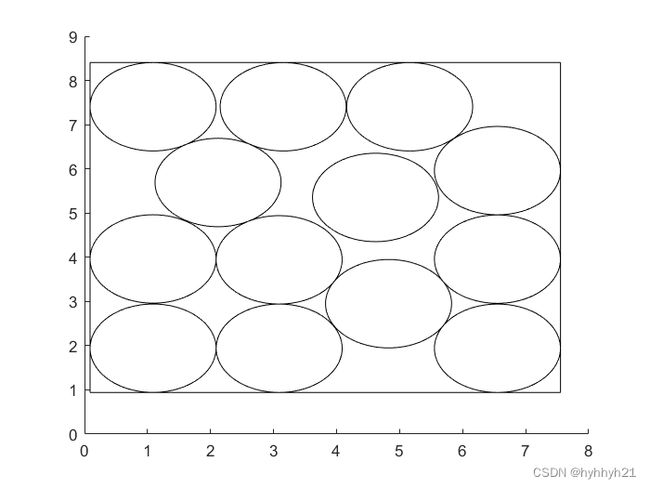
N=47的情况:
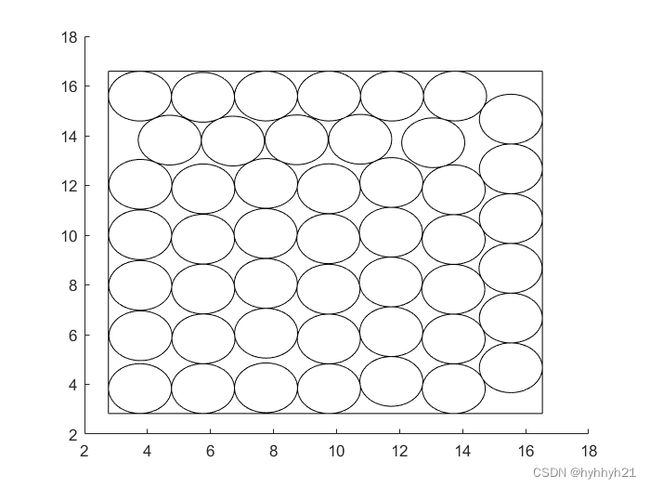
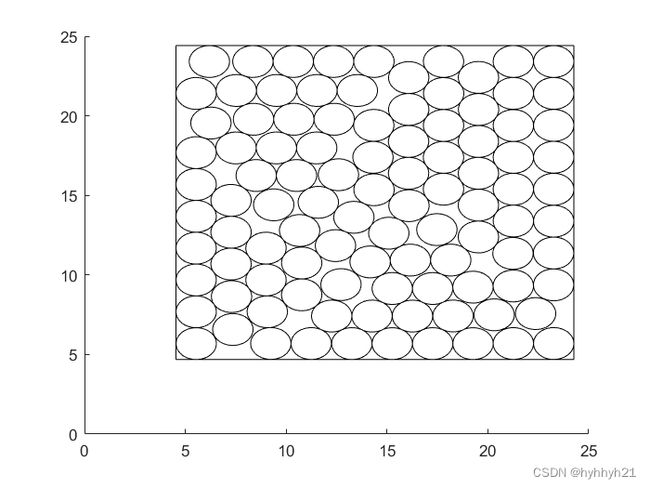
N=100的情况,出乎意料最密堆积不是10×10的方形堆积结构,而是更倾向于六边形的六方堆积结构,这里给出的最小正方形边长为19.7。这个解并不是最优解,因为这个正方形里面感觉还有不少空隙可以填充。
目前的最优解是05年得到的,最终正方形边长为19.45,参考来源我前言给的那个网站。
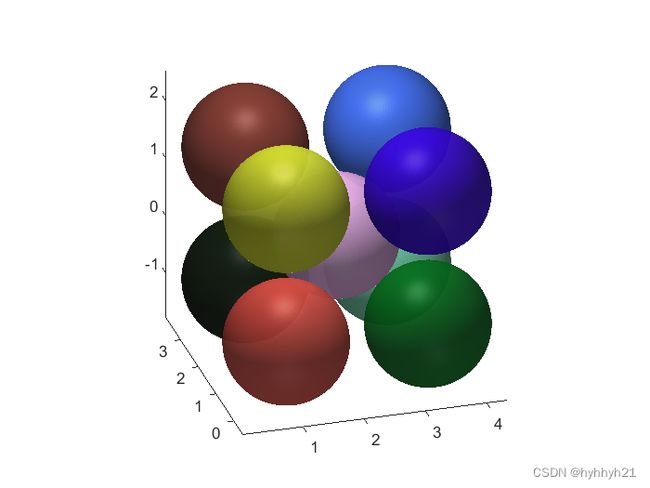
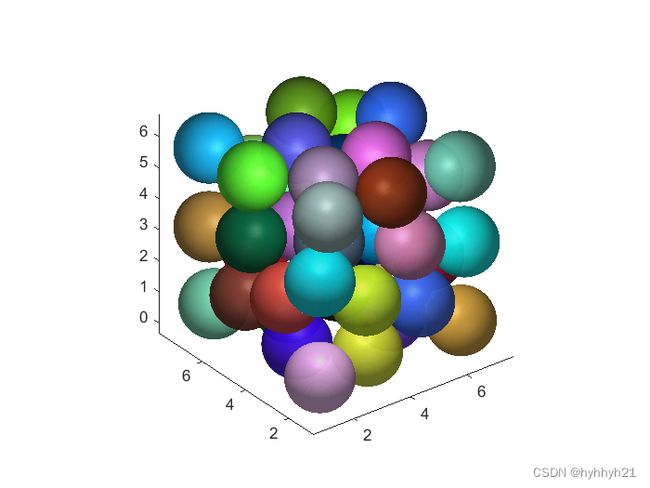
2 N个球的最小外接立方体求解
这里其实就是把上面代码中的2D换为3D,然后把各个函数也对应更改了一下,具体计算方法没有太多变化。
代码如下:
clear
clc
close all
%计算球的最小外接正方体3D
%利用fmincon算法
%求解函数最小值
N=9;
fun = @MinValue;
lb = -2*ones(1,N*3);%[xi,yi,zi,xi,yi,zi,...]
ub = (4*N^(1/3)-2)*ones(1,N*3);
%小球半径为1
A = [];
b = [];
Aeq = [];
beq = [];
%按照网格布置初始圆
NMesh=ceil(N^(1/3));
[XMesh,YMesh,ZMesh]=meshgrid(0:4:(4*NMesh-1),0:4:(4*NMesh-1),0:4:(4*NMesh-1));
XYMesh=[XMesh(:),YMesh(:),ZMesh(:)]';
x0=XYMesh(1:3*N);
x0=x0+rand(1,3*N)-0.5;%添加随机性
nonlcon = @NolinearCondition;%设定非线性约束条件
options = optimoptions('fmincon','Display','iter','Algorithm','interior-point','MaxFunctionEvaluations',inf);
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options);
%放大圆形,然后再计算一次。相当于让圆膨胀一下,然后利用约束条件再迭代一下
x=x/1.2;
options = optimoptions('fmincon','Display','iter','Algorithm','sqp','MaxFunctionEvaluations',inf,'MaxIterations',1e5);
x = fmincon(fun,x,A,b,Aeq,beq,lb,ub,nonlcon,options);
%放大圆形,然后再计算一次。相当于让圆膨胀一下,然后利用约束条件再迭代一下
x=x/1.05;
x = fmincon(fun,x,A,b,Aeq,beq,lb,ub,nonlcon,options);
figure()
camlight('headlight')
hold on
for k=1:N
[X,Y,Z] = ellipsoid(x(k*3-2),x(k*3-1),x(k*3),1,1,1,100);
h=surf(X,Y,Z,'EdgeColor','none','FaceColor',gallery('uniformdata',[1,3],k),...
'FaceAlpha',0.8);
h.DiffuseStrength=0.8;
h.SpecularStrength=0.2;
end
view(3)
axis equal
%非线性约束
function [c,ceq] = NolinearCondition(x)
%格式固定,c(x) ≤ 0 和 ceq(x) = 0。如果没有就是[]
N=length(x)/3;%点的数量
%转化坐标
xyz=zeros(3,N);
xyz(:)=x(:);
xyz=xyz';
%计算距离
DAll=pdist(xyz,'squaredeuclidean');%距离的平方(这样省去了根号,加快计算速度)
%N个小球之间不碰撞,计算所有的负距离之和
DAll=DAll-1*4;
DNeg=sum(DAll(DAll<0));
%要让c<=0
c = -DNeg;%
ceq = [];
end
%评价函数
function V=MinValue(x)
%求包围很多球体的最小立方体
%x=[x1,y1,x2,y2,....]
%N=length(x)/2;%点的数量
%半径为1的圆
minX=min(x(1:3:end-2))-1;
maxX=max(x(1:3:end-2))+1;
minY=min(x(2:3:end-1))-1;
maxY=max(x(2:3:end-1))+1;
minZ=min(x(3:3:end-0))-1;
maxZ=max(x(3:3:end-0))+1;
%计算立方体边长
L=max([maxX-minX,maxY-minY,maxZ-minZ]);
V=L;
end
然后看一下输出结果: