方形平板振动克拉尼图形可视化计算MATLAB程序(Chladni Patterns)
方形平板振动克拉尼图形可视化计算MATLAB程序(Chladni Patterns)
- 0前言
- 1 数值时域求解
-
- 1.1 方程建立
- 1.2 数值差分方程建立
- 1.3 计算结果
- 2 简单的波动解
- 3 理论求解
惯例声明:本人没有相关的工程应用经验,只是纯粹对相关算法感兴趣才写此博客。所以如果有错误,欢迎在评论区指正,不胜感激。本文主要关注于算法的实现,对于实际应用等问题本人没有任何经验,所以也不再涉及。
0前言
克拉尼图形(Chladni Patterns)是在1787年,由克拉尼首先发现并命名的。他将一个金属薄板中央固定,然后把细沙撒在金属板上,用小提琴摩擦边缘,板子上的细沙便会形成各种不同的图案。
相关的实验非常多,很多科技馆或者大学实验课或者网上视频大家也都接触过。具体原理也不难,就是每种频率下方板的振动模态是固定的,有的地方振动幅度大,有的地方振动幅度小,沙子在不断上下颠的过程中肯定会逐渐往振动小的地方汇集,于是就形成了克拉尼图形。
所以要想数值求解克拉尼图形,最重要的还是要求解出相应的振动方程才行。
本博客将求解方法分为3种,分别对应网上或者论文中常见的求解方式。相应文献这次就不放到前言了,放到后面每一章的开头。
下面的代码涉及到简单的数值分析基础,有些基础知识可能不会详细涉及。
1 数值时域求解
最近解微分方程比较上头,所以这里也顺手写了一个,效率比较低。
参考文献:
[1] 弹性力学(下册)(徐芝纶版) (第十四章:用差分法及变分法解薄板的小挠度弯曲问题)
[2] Abdeljaber O , Rjoub Y A . Free and forced vibration of rectangular plates using the finite difference method[C]// Green Building, Materials and Civil Engineering. 2014.
1.1 方程建立
根据常见的克拉尼图形实验来看,这属于弹性力学里的薄板小变形问题。
薄板静变形方程为:
∇ 4 u = ∂ 4 u ∂ x 4 + 2 ∂ 4 u ∂ x 2 ∂ y 2 + ∂ 4 u ∂ y 4 = 0 \nabla ^4u= \frac{\partial^4 u}{\partial x^4}+2\frac{\partial^4 u}{\partial x^2\partial y^2}+\frac{\partial^4 u}{\partial y^4}=0 ∇4u=∂x4∂4u+2∂x2∂y2∂4u+∂y4∂4u=0
其中u为薄板变形位移。当然,本文只考虑垂直于平板表面的位移,其余位移忽略。
再考虑运动,还需要引入时间t和加速度对应的量,方程变为:
∇ 4 u + ρ h D ∂ 2 u ∂ t 2 = 0 \nabla ^4u+\frac{\rho h}{D} \frac{\partial^2 u}{\partial t^2}= 0 ∇4u+Dρh∂t2∂2u=0
其中 D = E h 3 / 12 ( 1 − μ ) 2 D=Eh^3 /12(1-\mu)^2 D=Eh3/12(1−μ)2,E为平板材料的弹性模量,μ为材料的泊松比,ρ为材料的密度,这都是材料属性。h为薄板的厚度。
平板位置为在xy平面的[-L,L]区间上,四周为自由边界条件。
平板中心(0,0)点的位置为固定边界条件,中间固定点位移为已知的余弦函数振动。
为简化计算量,后面1.2节将平板沿x轴和y轴裁剪为1/4对称的小方形,中间设置为对称边界条件。
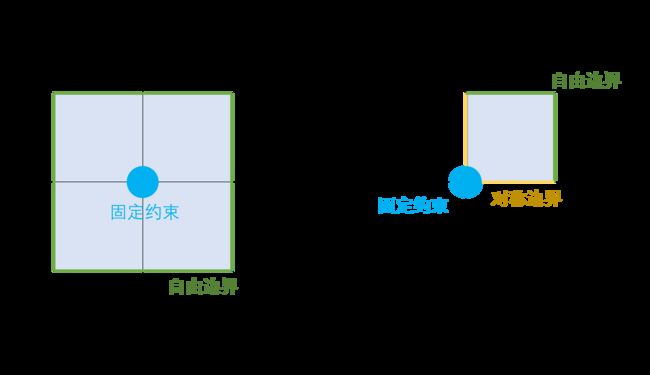
这种1/4模型简化有一定的问题,比如当平板做非对称振动时就无法模拟,而且Chladni图形的实验中也观察到这种图形。这个在后面第2章和第3章会涉及。
1.2 数值差分方程建立
首先 ∇ 4 u \nabla ^4u ∇4u,我们直接采用下面的差分格式:

这里假设dx和dy方向的网格尺寸相同。当然,上面的表达式也并非唯一,这种13点差分格式的优点为结构比较紧凑,用到的点比较少,其余格式也可以自行泰勒展开凑一凑。
时间项由于只有二阶,所以更简单一些:
∂ 2 u ∂ t 2 → u t − 2 − 2 u t − 1 + u t d t 2 \frac{\partial^2 u}{\partial t^2} \to \frac{u_{t-2}-2u_{t-1}+u_{t}}{dt^2} ∂t2∂2u→dt2ut−2−2ut−1+ut
之后将上面所有单元的对应的差分方程列出后,将显示时间格式项加入方程中,然后联立这些方程组得到当前时刻的空间u。每个单元格点的方程u表示如下:
( 20 + ρ h D d x 4 d t 2 ) u m , n , t − 8 ( u m − 1 , n , t + u m + 1 , n , t + u m , n − 1 , t + u m , n + 1 , t ) (20+\frac{\rho h}{D}\frac{dx^4}{dt^2})u_{m,n,t} -8(u_{m-1,n,t}+u_{m+1,n,t}+u_{m,n-1,t}+u_{m,n+1,t}) (20+Dρhdt2dx4)um,n,t−8(um−1,n,t+um+1,n,t+um,n−1,t+um,n+1,t)
+ 2 ( u m − 1 , n − 1 , t + u m − 1 , n + 1 , t + u m + 1 , n + 1 , t + u m + 1 , n − 1 , t ) +2(u_{m-1,n-1,t}+u_{m-1,n+1,t}+u_{m+1,n+1,t}+u_{m+1,n-1,t}) +2(um−1,n−1,t+um−1,n+1,t+um+1,n+1,t+um+1,n−1,t)
+ ( u m − 2 , n , t + u m + 2 , n , t + u m , n − 2 , t + u m , n + 2 , t ) +(u_{m-2,n,t}+u_{m+2,n,t}+u_{m,n-2,t}+u_{m,n+2,t}) +(um−2,n,t+um+2,n,t+um,n−2,t+um,n+2,t)
= ρ h D d x 4 d t 2 ( 2 u m , n , t − 1 − u m , n , t − 2 ) =\frac{\rho h}{D}\frac{dx^4}{dt^2}(2u_{m,n,t-1}-u_{m,n,t-2}) =Dρhdt2dx4(2um,n,t−1−um,n,t−2)
最终,整理为:
K ∗ U = F K*U=F K∗U=F
其中U为列向量,由前面网格位置 u m , n u_{m,n} um,n组成,是未知数。K为一个系数方阵,每一行为对应的 u m , n u_{m,n} um,n网格相应的系数。F为每个网格的受力,也是一个列向量。
最终根据K和F,求解线性方程组,就可以求解出网格位置U。
当然,只有方程还是不行的,微分方程另一个老大难就是边界条件(甚至很多问题边界条件比方程本身还难)。
因为前面 ∇ 4 u \nabla ^4u ∇4u用的13点差分格式,用到了上下左右向外方向上的2个距离的格点,所以为了能够顺利计算,就需要在平板的边缘外再补2圈虚拟节点。虚拟节点只与平板边缘的边界条件有关,所以时间项也都忽略为0。
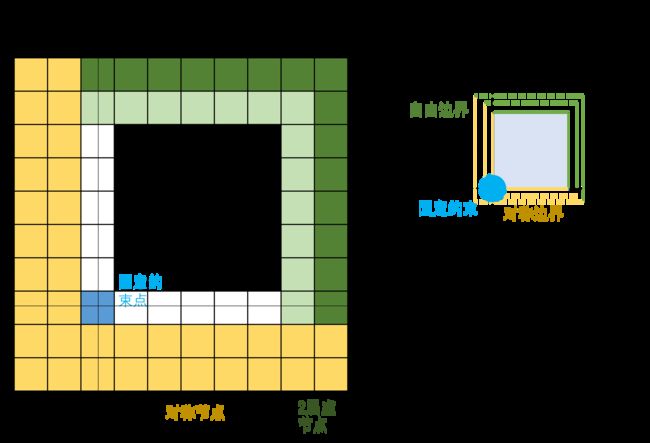
首先是对称边界条件,这个很简单,就是沿着对称轴对称就行。下面以左右对称边界条件的格点方程为例:
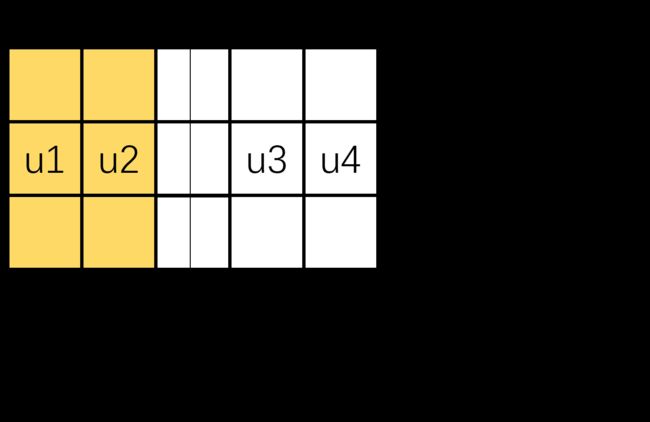
然后是外侧自由无约束边界条件,第一层虚拟节点可以用内力M=0列方程得到:
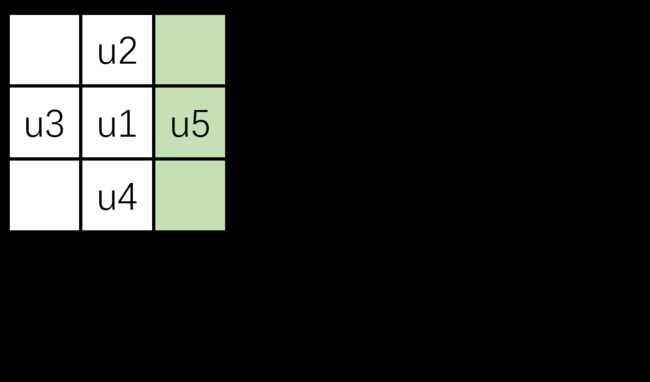
对于平板四个角,只用Mx和My不能完全得到对应的方程,还需要引入Mxy=0

平板的角上第一层虚节点还差两个格点没有给出,再根据对称假设,假设沿对角线对称且Mx=My=0,得到:

第二层虚节点,我们用分布反力V=0来列出方程:
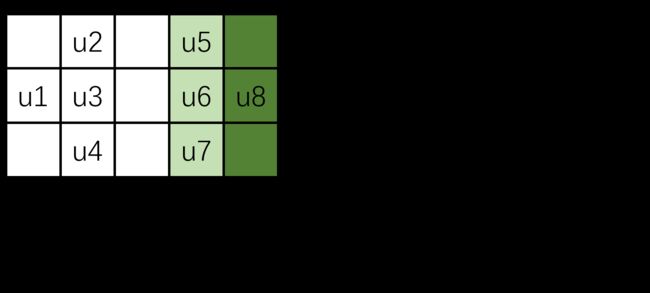
第二层虚节点在右上角还有3个节点没有方程涉及到,因为不涉及计算,所以全部强制赋值0即可。
因此,我们便得到了所有网格单元的方程,比如1/4平板网格数为6×6,加上两层虚节点,网格数变为10×10。算上前面列的方程,每个网格点都有一个独立的方程,因此我们便得到了100个线性方程。之后求解这个100个方程KU=F的方程组,就得到每个网格点的位置U。
这一段可能稍微啰嗦一些,但是如果想要动手编程计算的话,还是很难跳过的。
1.3 计算结果
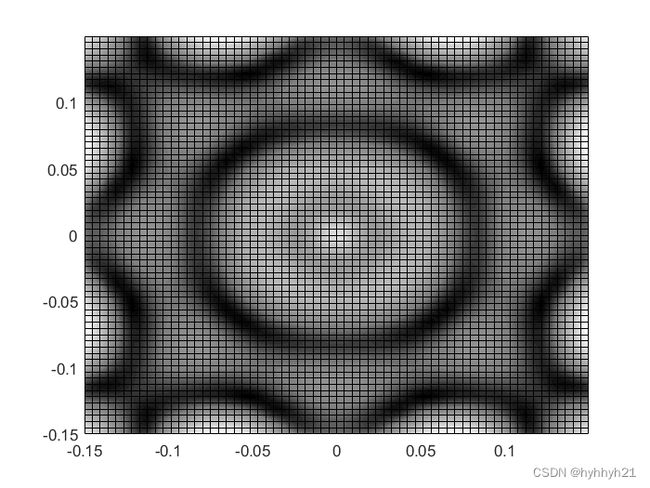
之后是MATLAB计算仿真的结果,为完整展示振动图形,将1/4板做完整对称处理。虚拟节点没有展示。
这里只计算0.03s几个振动周期的平均结果,时间步长为1e-6s,空间网格点为16(对称完后为31个点)。
下图为792hz对应的结果:
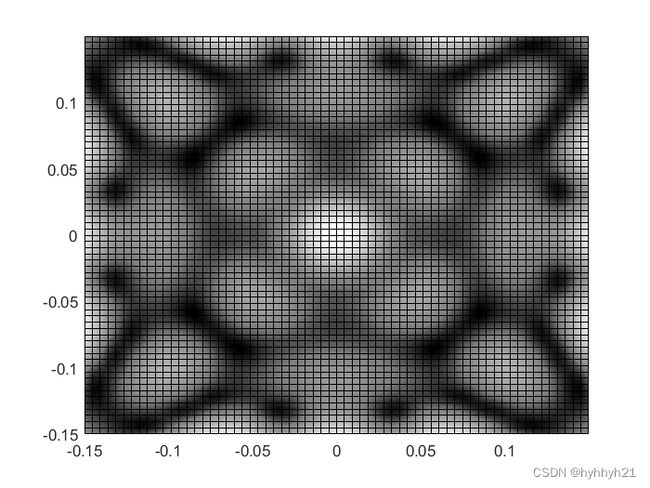
下图为850hz对应的结果:

可以看到振动频率越高,图形越复杂。
这意味着频率越高,需要的空间网格量越大,而且频率越高,需要更小的时间步长。因此这种方法在高频率振动时,不是可行的展示办法。但在低频的时候,还是比较精准的。
代码如下,这里自己添加了一个阻尼项,因为如果不添加,平板振幅会越振越大。
clear
clc
close all
%平板信息
L=0.150;%边长300mm
h=0.001;%厚度10mm
mu=0.33;%泊松比0.33
rho=2.7e3;%板子的密度
E=70e9;%弹性模量
D=E*h^3/12/(1-mu^2);
%振动信息
Amp=0.01;
Freq=650;%频率越高,需要的网格越密。参考Freq=792,N=16。Freq=400,N=8。
%构建网格
dt=1e-6;%时间步长%1000hz的话,就是
N=16;%偶数%网格总数量为N*N,节点数目N+1*N+1
dx=L/N;%网格大小
x=dx*(0:N);
[X,Y]=meshgrid(x,x);%生成方形网格
%列方程组
[Sq,Bq]=Equation_Sq0(N,mu,-Amp);%初始值为-0.1的无外力分布
%已知Sq*U=Bq;%求U的分布,U即是当前平板上每一个点的位移
U0=Sq\Bq;
U1=U0;
U2=U1;
U_Out1=zeros(N+1,N+1);
U_Out2=zeros(N+5,N+5);
U_Save=zeros((N+1)^2,200);t_Save=1;
%计算动态方程
t_start=0;t_end=0.03;%起始时间和终止计算时间
jishu=1;%用于计数的一个变量
N_jishu=(t_end-t_start)/dt;
for t_k=t_start:dt:t_end
%0点处的运动位置
u0=Amp*cos(2*pi*Freq*t_k+pi);%以正弦方式运动
L_Sq=N+5;%实际计算时网格的尺寸(包含外侧扩展的两层)
if jishu==1%第一步计算,把矩阵Sq计算出来
[Sq,Bq]=Equation_Sq0(N,mu,u0);%初始值为-0.1的无外力分布
%补充运动项,把U1,U2代入,计算U3
for k=1:L_Sq^2
[r_k,c_k]=ind2sub([L_Sq,L_Sq],k);
if (r_k>=3 && r_k<=L_Sq-2) && (c_k>=3 && c_k<=L_Sq-2)
Sq(k,k)=20+rho*h*dx^4/D/dt^2;
Sq(k,[k+1,k-1,k+L_Sq,k-L_Sq])=-8;
Sq(k,[k+L_Sq+1,k+L_Sq-1,k-L_Sq+1,k-L_Sq-1])=2;
Sq(k,[k+2,k-2,k-2*L_Sq,k+2*L_Sq])=1;
Fd=-100*sign(U2(k)-U1(k))*(U2(k)-U1(k))^2/dt^2;%增加阻尼项
Bq(k)=dx^4/D*(rho*h/dt^2*(2*U2(k)-U1(k))+Fd);
end
end
%再重新定义一下中心约束点
Indx_Center=sub2ind([L_Sq,L_Sq],3,3);
Sq(Indx_Center,:)=0;Sq(Indx_Center,Indx_Center)=1;
Bq(Indx_Center)=u0; %初始值为-0.1
%Sq=sparse(Sq);转换为稀疏矩阵的形式,会让计算稍微快一些
else
%其余情况Sq矩阵不会变化,所以不用重复计算
for k=1:L_Sq^2
[r_k,c_k]=ind2sub([L_Sq,L_Sq],k);%这一块还可以优化,让速度更快一点
if (r_k>=3 && r_k<=L_Sq-2) && (c_k>=3 && c_k<=L_Sq-2)
Fd=-100*sign(U2(k)-U1(k))*(U2(k)-U1(k))^2/dt^2;%增加阻尼项
Bq(k)=dx^4/D*(rho*h/dt^2*(2*U2(k)-U1(k))+Fd);
end
end
Bq(1+2+2*L_Sq)=u0; %固定位置随u0变化
end
U3=Sq\Bq;
%定义前两个时间步长下的位置信息
U1=U2;
U2=U3;
%储存,用作输出用
U_Out2(:)=U3(:);
U_Out=U_Out2(3:end-2,3:end-2);
% if mod(jishu,100)==1
% figure(1)
% clf
% %pcolor(X,Y,U_Out)
% mesh(X,Y,U_Out)
% caxis([-0.2,0.2])
% zlim([-0.2,0.2])
% colorbar
% pause(0.1)
% disp(t_k)
% end
jishu=jishu+1;%时间步加一
%记最后200个数据储存
if jishu+50*200>=N_jishu
if mod(jishu,50)==1
U_Save(:,t_Save)=U_Out(:);
t_Save=t_Save+1;
end
end
end
%取一些特征点,观察计算情况
figure()
hold on
for k=1:size(U_Save,1)
plot(U_Save(k,:))
end
hold off
%填充对称图形
U_Out_A=U_Out;
U_Out_A(:)=max(U_Save,[],2)-min(U_Save,[],2);
U_Out_A2=[fliplr(U_Out_A(:,2:end)),U_Out_A];
U_Out_A3=[flipud(U_Out_A2(2:end,:));U_Out_A2];
%绘制
figure()
x3=dx*(-N:N);
[X3,Y3]=meshgrid(x3,x3);
mesh(X3,Y3,U_Out_A3)
%插值绘制(网格太稀疏了,绘图效果不好看,还是要插值一下)
xp=dx/2*(-2*N:2*N);
[Xp,Yp]=meshgrid(xp,xp);
F=griddedInterpolant(X3',Y3',U_Out_A3','spline');
U_Out_p=F(Xp,Yp);
figure()
sp=pcolor(Xp,Yp,U_Out_p);
mcp=[[linspace(0,0.5,16)',linspace(0,0.5,16)',linspace(0,0.5,16)'];
[linspace(0.5,1,32)',linspace(0.5,1,32)',linspace(0.5,1,32)'];
[1,1,1];[1,1,1]];
colormap(mcp)
sp.FaceColor = 'interp';
function [Sq,Bq]=Equation_Sq0(N,mu,u0)
%N网格数目
%mu泊松比
%u0初始平板位置
%外拓展两圈后平板网格的索引
L_Sq=N+5;
%角落边界点,都设置为0
Point_Corner0=[L_Sq,L_Sq;L_Sq-1,L_Sq;L_Sq,L_Sq-1];
%自由角垂直外边界,共2个
Point_CornerC=[L_Sq-1,L_Sq-2;L_Sq-2,L_Sq-1];
%第一层边界点(非对称)
Point_Out1=[(L_Sq-1)*ones(L_Sq-5,1),(3:L_Sq-3)';...
(3:L_Sq-3)',(L_Sq-1)*ones(L_Sq-5,1)];
%对角线外边界,共1个
Point_Corner=[L_Sq-1,L_Sq-1];
%第二层边界点
Point_Out2=[L_Sq*ones(L_Sq-4,1),(3:L_Sq-2)';...
(3:L_Sq-2)',L_Sq*ones(L_Sq-4,1)];
%第一层对称边界
Point_Mirror1=[2*ones(L_Sq-2,1),(3:L_Sq)';...
(3:L_Sq)',2*ones(L_Sq-2,1)];
%第二层对称边界
Point_Mirror2=[1*ones(L_Sq-2,1),(3:L_Sq)';...
(3:L_Sq)',1*ones(L_Sq-2,1)];
%左上角对称边界
Point_MirrorC=[1,1;1,2;2,1;2,2];
Sq=zeros(L_Sq^2);
Bq=zeros(L_Sq^2,1);
for k=1:L_Sq^2
[r_k,c_k]=ind2sub([L_Sq,L_Sq],k);
%四周边界点
%四周角落边界点,都设置为0
if IsRowInRowList(Point_Corner0,[r_k,c_k])
Sq(k,k)=1;
Bq(k)=0;
end
%自由角垂直外边界
if IsRowInRowList(Point_CornerC,[r_k,c_k])
if r_k==2
Sq(k,k:k+2)=[1,-2,1];
elseif r_k==L_Sq-1
Sq(k,k-2:k)=[1,-2,1];
elseif c_k==2
Sq(k,[k,k+L_Sq,k+2*L_Sq])=[1,-2,1];
elseif c_k==L_Sq-1
Sq(k,[k-2*L_Sq,k-L_Sq,k])=[1,-2,1];
end
Bq(k)=0;
%计算第一层边界点
elseif IsRowInRowList(Point_Out1,[r_k,c_k])
if r_k==2 %My=0
Sq(k,[k+1-L_Sq,k+1,k+1+L_Sq])=[-mu,2+2*mu,-mu];
Sq(k,k)=-1;Sq(k,k+2)=-1;
elseif r_k==L_Sq-1 %My=0
Sq(k,[k-1-L_Sq,k-1,k-1+L_Sq])=[-mu,2+2*mu,-mu];
Sq(k,k)=-1;Sq(k,k-2)=-1;
elseif c_k==2 %Mx=0
Sq(k,[k,k+L_Sq,k+2*L_Sq])=[-1,2+2*mu,-1];
Sq(k,k+L_Sq-1)=-mu;Sq(k,k+L_Sq+1)=-mu;
elseif c_k==L_Sq-1 %Mx=0
Sq(k,[k,k-L_Sq,k-2*L_Sq])=[-1,2+2*mu,-1];
Sq(k,k-L_Sq-1)=-mu;Sq(k,k-L_Sq+1)=-mu;
end
Bq(k)=0;
%自由角对角线外边界,每个角1个
elseif IsRowInRowList(Point_Corner,[r_k,c_k])
if r_k==2 && c_k==2
Sq(k,[k,k+2*L_Sq+2])=[1,1];
Sq(k,[k+2,k+2*L_Sq])=[-1,-1];
elseif r_k==L_Sq-1 && c_k==2
Sq(k,[k,k+2*L_Sq-2])=[1,1];
Sq(k,[k-2,k+2*L_Sq])=[-1,-1];
elseif r_k==2 && c_k==L_Sq-1
Sq(k,[k,k-2*L_Sq+2])=[1,1];
Sq(k,[k+2,k-2*L_Sq])=[-1,-1];
elseif r_k==L_Sq-1 && c_k==L_Sq-1
Sq(k,[k,k-2*L_Sq-2])=[1,1];
Sq(k,[k-2,k-2*L_Sq])=[-1,-1];
end
Bq(k)=0;
%4计算第二层边界点
elseif IsRowInRowList(Point_Out2,[r_k,c_k])
if r_k==1
Sq(k,k)=1;
Sq(k,[k+1-L_Sq,k+1,k+1+L_Sq])=[2-mu,2*mu-6,2-mu];
Sq(k,[k+3-L_Sq,k+3,k+3+L_Sq])=[mu-2,-2*mu+6,mu-2];
Sq(k,k+4)=-1;
elseif r_k==L_Sq
Sq(k,k)=1;
Sq(k,[k-1-L_Sq,k-1,k-1+L_Sq])=[2-mu,2*mu-6,2-mu];
Sq(k,[k-3-L_Sq,k-3,k-3+L_Sq])=[mu-2,-2*mu+6,mu-2];
Sq(k,k-4)=-1;
elseif c_k==1
Sq(k,k)=1;
Sq(k,[k+L_Sq-1,k+L_Sq,k+L_Sq+1])=[2-mu,2*mu-6,2-mu];
Sq(k,[k+3*L_Sq-1,k+3*L_Sq,k+3*L_Sq+1])=[mu-2,-2*mu+6,mu-2];
Sq(k,k+4*L_Sq)=-1;
elseif c_k==L_Sq
Sq(k,k)=1;
Sq(k,[k-L_Sq-1,k-L_Sq,k-L_Sq+1])=[2-mu,2*mu-6,2-mu];
Sq(k,[k-3*L_Sq-1,k-3*L_Sq,k-3*L_Sq+1])=[mu-2,-2*mu+6,mu-2];
Sq(k,k-4*L_Sq)=-1;
end
Bq(k)=0;
%计算除边界点外的正常平板上的点
elseif (r_k>=3 && r_k<=L_Sq-2) && (c_k>=3 && c_k<=L_Sq-2)
Sq(k,k)=20;
Sq(k,[k+1,k-1,k+L_Sq,k-L_Sq])=-8;
Sq(k,[k+L_Sq+1,k+L_Sq-1,k-L_Sq+1,k-L_Sq-1])=2;
Sq(k,[k+2,k-2,k-2*L_Sq,k+2*L_Sq])=1;
Bq(k)=0;%dx^4/D*(rho*h/dt^2*(2*0-0));
%计算对称边界的外插点
elseif IsRowInRowList(Point_Mirror1,[r_k,c_k])
if r_k==2
Sq(k,k)=1;Sq(k,k+2)=-1;
elseif c_k==2
Sq(k,k)=1;Sq(k,k+2*L_Sq)=-1;
end
Bq(k)=0;
elseif IsRowInRowList(Point_Mirror2,[r_k,c_k])
if r_k==1
Sq(k,k)=1;Sq(k,k+4)=-1;
elseif c_k==1
Sq(k,k)=1;Sq(k,k+4*L_Sq)=-1;
end
Bq(k)=0;
elseif IsRowInRowList(Point_MirrorC,[r_k,c_k])
if r_k==1 && c_k==1
Sq(k,k)=1;Sq(k,k+4+4*L_Sq)=-1;
elseif r_k==1 && c_k==2
Sq(k,k)=1;Sq(k,k+4+2*L_Sq)=-1;
elseif r_k==2 && c_k==1
Sq(k,k)=1;Sq(k,k+2+4*L_Sq)=-1;
elseif r_k==2 && c_k==2
Sq(k,k)=1;Sq(k,k+2+2*L_Sq)=-1;
end
Bq(k)=0;
end
end
% Sq([32,41,42],:)=[];Bq([32,41,42])=[];
% rank(Sq)%检查是否满秩
%补充两个边界约束(中心点已知,)
%初始已知中心点坐标
Sq(1+2+2*L_Sq,:)=0;Sq(1+2+2*L_Sq,1+2+2*L_Sq)=1;
Bq(1+2+2*L_Sq)=u0; %初始值为-1
end
function TF=IsRowInRowList(List,Point)
TF1=(List(:,1)==Point(1));
TF= any(List(TF1,2)==Point(2));
end
方程建立有几点小的心得体会:
1是要寻找一种让矩阵Sq保持不变的方程形式,这种矩阵在力学求解器或者其它方程求解器中很常见,比如刚度矩阵、气动矩阵等等。
2这里为了方便展示和检查,在代码中把Sq=sparse(Sq);这个注释掉了。实际上Sq矩阵是一个稀疏矩阵,在matlab中转换成稀疏矩阵格式,可以显著的减少内存加速计算。
3方程的建立初期还是比较痛苦的,需要检查是否满秩,约束是否刚好够。比如全模型的方程很容易列出少约束的情况,这时就需要找到哪些方程是重复无用的方程(比如中间固定点旁边的几个点,就可以用对称或反对称边界条件替换原物理方程)。
2 简单的波动解
参考文献:
[1]关于Chladni图案
https://zhuanlan.zhihu.com/p/108448193
[2]Creating Digital Chladni Patterns
https://thelig.ht/chladni/
这里我们做一个大胆的假设,平板上每一个点都在做周期运动sin(wt+k),而且相位差不多,只是振幅大小不同。
那么,我们不需要知道上一章所列的平板振动方程,也可以大概列出平板方程的通解。
设平板上每一点的振幅为u(x,y,t),可以表示为:
u ( x , y , t ) = w ( x , y ) ∗ sin ( w t + k ) u(x,y,t)=w(x,y)*\sin(wt+k) u(x,y,t)=w(x,y)∗sin(wt+k)
w(x,y)是平板上每个点的振幅。当然后面那个w(频率)和k(相位)我们不关心,因为后面用不到。
如果我们知道每个点对应的振幅,那么振幅等于0的位置就是Chladni图案。所以下一步我们就计算振幅w(x,y)的通解。
现在建立平板模型,设平板的范围为[-0.5,0.5],中心点为(0,0)。平板的边缘自由振动。
假定w(x,y)是由若干个余弦波叠加而成的。而平板要想形成共振,需要承载较为完整的驻波。所以X方向大致满足条件的解可以有如下的表示方式:
X ( x ) = cos ( n π ( x − 0.5 ) ) X(x)=\cos(n\pi (x-0.5)) X(x)=cos(nπ(x−0.5))
其中n为方形板上x方向波峰和波谷总和的数量。这里假定平板的边缘在余弦函数的峰或谷上。Y方向同理。
振动时,具体w(x,y)的振幅由当地的X(x)和Y(y)相乘决定,即:
cos ( n π ( x − 0.5 ) ) ∗ cos ( m π ( y − 0.5 ) ) \cos(n\pi (x-0.5))*\cos(m\pi (y-0.5)) cos(nπ(x−0.5))∗cos(mπ(y−0.5))
n和m不一定相同。因此考虑x和y的对称性,m和n对换的情况也会同时叠加出现。最终振幅w(x,y)的方程为
w ( x , y ) = cos ( n π ( x − 0.5 ) ) ∗ cos ( m π ( y − 0.5 ) ) ± cos ( m π ( x − 0.5 ) ) ∗ cos ( n π ( y − 0.5 ) ) w(x,y)=\cos(n\pi (x-0.5))*\cos(m\pi (y-0.5)) \\ \pm \cos(m\pi (x-0.5))*\cos(n\pi (y-0.5)) w(x,y)=cos(nπ(x−0.5))∗cos(mπ(y−0.5))±cos(mπ(x−0.5))∗cos(nπ(y−0.5))
上面式子中正号代表对称图案情况,负号代表反对称图案情况。
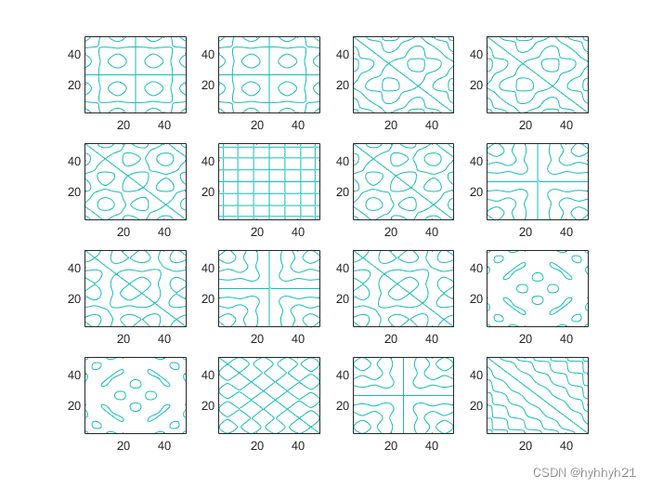
最终不同m和n取值下,生成的Chladni图案如下:
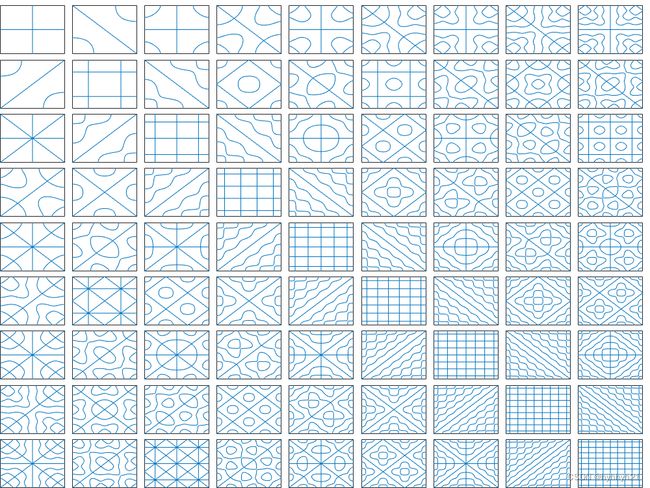
根据某些文献中给出的Chladni’s Law,可以根据生成的图案来大概反推频率:
f ∼ ( m + 2 n ) 2 f\sim (m+2n)^2 f∼(m+2n)2
也就是频率f和(m+2n)的平方成正比。
上图的matlab代码如下:
clear
clc
close all
%绘制所有可能波节的输出结果
N=9;
figure(1)
for m=1:N
for n=1:N
%ax=subplot(N,N,N*(m-1)+n);
dp=1/N;
ax=subplot('Position',[(m-1)*dp 1-(n-0)*dp 0.9*dp 0.9*dp]);
fun1=@(x,y) cos(n*pi*(x-0.5)).*cos(m*pi*(y-0.5));
fun2=@(x,y) cos(m*pi*(x-0.5)).*cos(n*pi*(y-0.5));
fun=@(x,y) fun1(x,y)+sign(m-n)*fun2(x,y);
fimplicit(fun,[-0.5,0.5])
ax.XTick=[];
ax.YTick=[];
end
end
set(gcf,'position',[100,100,800,600])
3 理论求解
参考文献:
[1]方奕忠, 王钢, 沈韩,等. 方形薄板二维驻波的研究[J]. 物理实验, 2014
[2]Neville H. Fletcher , Thomas D. Rossing .The Physics of Musical Instruments [M] ISBN-13:978-0-387-94151-6
[3]严琪琪, 陈彦, 胡湘. 自由边界条件下方形平板受迫振动模式的探究[J]. 大学物理, 2018
当然,上面的方程还是太过于简化,下面给出了一种能够较好预测出结果的一种理论解方法。下面方程参考参考文献[1]方形薄板二维驻波的研究。(其实[3]自由边界条件下方形平板受迫振动模式的探究 那篇文章的效果看上去更好,但是我没太看懂 (╯°Д°)╯︵┻━┻,先用简单的顶上)。
首先还是需要求解下面这个方程:
∇ 4 u + 1 c 2 ∂ 2 u ∂ t 2 = 0 \nabla ^4u+\frac{1}{c^2} \frac{\partial^2 u}{\partial t^2}= 0 ∇4u+c21∂t2∂2u=0
依然假设方程的解为:
u ( x , y , t ) = w ( x , y ) ∗ sin ( ω t + k ) u(x,y,t)=w(x,y)*\sin(\omega t+k) u(x,y,t)=w(x,y)∗sin(ωt+k)
代入回方程,可以得到关于振幅w(x,y)的方程:
∇ 4 w − γ 2 w = 0 \nabla ^4w-\gamma ^2 w= 0 ∇4w−γ2w=0
在x=0和x=1的边界条件为:
∂ 2 w ∂ x 2 + μ ∂ 2 w ∂ y 2 = 0 ∂ ∂ x ( ∂ 2 w ∂ x 2 + ( 2 − μ ) ∂ 2 w ∂ y 2 ) = 0 \frac{\partial^2 w}{\partial x^2}+ \mu\frac{\partial^2 w}{\partial y^2}=0\\ \frac{\partial }{\partial x }(\frac{\partial^2 w}{\partial x^2}+ (2-\mu)\frac{\partial^2 w}{\partial y^2})=0 ∂x2∂2w+μ∂y2∂2w=0∂x∂(∂x2∂2w+(2−μ)∂y2∂2w)=0
在y=0和y=1的边界条件同理,为:
∂ 2 w ∂ y 2 + μ ∂ 2 w ∂ x 2 = 0 ∂ ∂ y ( ∂ 2 w ∂ y 2 + ( 2 − μ ) ∂ 2 w ∂ x 2 ) = 0 \frac{\partial^2 w}{\partial y^2}+ \mu\frac{\partial^2 w}{\partial x^2}=0\\ \frac{\partial }{\partial y }(\frac{\partial^2 w}{\partial y^2}+ (2-\mu)\frac{\partial^2 w}{\partial x^2})=0 ∂y2∂2w+μ∂x2∂2w=0∂y∂(∂y2∂2w+(2−μ)∂x2∂2w)=0
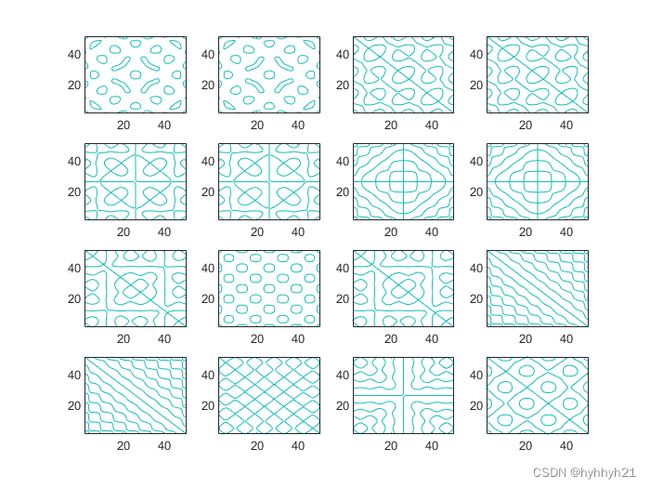
参考文献[1]的求解过程中也用到了一些简化,解的形式和上一章节比较像。由于本人没有具体实验,所以如何利用频率反推波节这一块,公式精度具体有多少,需要怎样修正,都是未知数。本文也不是论文,就不再做实验验证了。
理论上看该方法在较高频率预测效果应该会比较好。
clear
clc
close all
%绘制理论求解图形
%平板信息
L=0.5;
h=0.001;%厚度1mm
mu=0.33;
rho=2.7e3;%板子的密度
E=70e9;%弹性模量
D=E*h^3/12/(1-mu^2);
c=sqrt(E/rho)*h/sqrt(3)/sqrt(1-mu^2);%计算一个常数
%振动频率
f=1560;
%寻找可能的波节m和n
n_t=round(sqrt(f/pi/c*L^2)-0.5);
n_t1=n_t+(-8:8);
[m_t2,n_t2]=meshgrid(n_t1,n_t1);
MN2Freq=pi/2/L^2*c*((n_t2+0.5).^2+(m_t2+0.5).^2);%已知mn,反推频率的一个公式
[~,Ind_nt2]=sort(abs(MN2Freq(:)-f));
%得到接近当前频率的几组m和n。
[x,y]=meshgrid(0:0.01:L,0:0.01:L);
for k=1:16
%计算方程的解
mm=m_t2(Ind_nt2(k));
nn=n_t2(Ind_nt2(k));
%得到可能的mm值和nn值,然后计算出bn和bm。
bn=nn+0.5;
Ps1_n1=sqrt(2)/2*(exp(-pi*bn*x/L)-(-1)^nn*exp(pi*bn*(x-L)/L));
Ps1_n2=-sin(pi*bn/L*x-pi/4);
Ps1_n=Ps1_n1+Ps1_n2;
bm=mm+0.5;
Ps1_m1=sqrt(2)/2*(exp(-pi*bm*y/L)-(-1)^mm*exp(pi*bm*(y-L)/L));
Ps1_m2=-sin(pi*bm/L*y-pi/4);
Ps1_m=Ps1_m1+Ps1_m2;
Ps1_mn=Ps1_m.*Ps1_n;
%参照上一章,做出x和y交换后的另一组解
Ps2_n1=sqrt(2)/2*(exp(-pi*bn*y/L)-(-1)^nn*exp(pi*bn*(y-L)/L));
Ps2_n2=-sin(pi*bn/L*y-pi/4);
Ps2_n=Ps2_n1+Ps2_n2;
bm=mm+0.5;
Ps2_m1=sqrt(2)/2*(exp(-pi*bm*x/L)-(-1)^mm*exp(pi*bm*(x-L)/L));
Ps2_m2=-sin(pi*bm/L*x-pi/4);
Ps2_m=Ps2_m1+Ps2_m2;
Ps2_mn=Ps2_m.*Ps2_n;
%绘图
figure(1)
subplot(4,4,k)
contour(Ps1_mn+Ps2_mn,1)
end