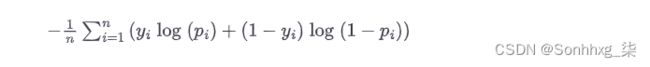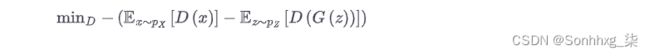【DL】第 3 章：生成对抗网络（GAN）

在本章中，您将：

• 了解生成对抗网络 (GAN) 的架构设计。

• 使用 Keras 从头开始构建和训练深度卷积 GAN (DCGAN)

• 使用 DCGAN 生成新图像

• 了解训练 DCGAN 时面临的一些常见问题

• 了解 Wasserstein GAN (WGAN) 架构如何解决这些问题

• 了解可以对 WGAN 进行的其他增强，例如将梯度惩罚 (GP) 项合并到损失函数中。

• 使用 Keras 从头开始构建 WGAN-GP

• 使用 WGAN-GP 生成人脸

• 了解条件 GAN (CGAN) 如何让您能够在给定标签上调整生成的输出。

• 在 Keras 中构建和训练 CGAN，并使用它来操作生成的图像。

2014 年，Ian Goodfellow 等人。在蒙特利尔举行的神经信息处理系统会议 (NeurIPS) 上发表了一篇题为“生成对抗网络” 论文。生成对抗网络（或更广为人知的 GAN）的引入现在被视为生成建模历史上的一个关键转折点，因为本文提出的核心思想催生了一些最成功和令人印象深刻的生成模型曾经创造过。

本章将首先阐述生成对抗网络 (GAN) 的理论基础。然后，您将学习如何使用 Keras 构建您自己的 GAN。

不过，首先，我们将再次使用一个小故事来说明 GAN 训练过程中使用的一些基本概念。

Armo Bricks 和 锻造者

假设这是您担任 Armo Bricks 质量控制主管的新工作的第一天，Armo Bricks 是一家专门生产各种形状和尺寸的优质积木的公司。Armo 产品的一些示例图片如图3.1 所示。

图3.1 装甲砖

您会立即收到关于生产线下线的某些产品出现问题的警报。竞争对手已开始仿制 Armo 积木，并找到了将它们混入客户收到的袋子中的方法。为了避免公关灾难和由此造成的收入损失，您决定将成为区分假冒砖块和真品砖块的专家作为您个人的首要任务，这样您就可以在生产线上拦截伪造的砖块提供给客户。

一开始这几乎是不可能的——您是新手，经验很少！然而，随着时间的推移，通过倾听客户反馈，您会逐渐变得更善于发现假货，并且您的收入损失开始下降。

伪造者对此并不满意——随着砖块买家回归值得信赖的 Armo 品牌，他们自己的客户群开始减少。他们通过对他们的伪造过程进行一些更改来响应您改进的检测能力，因此现在，真砖和假砖之间的区别对您来说更难发现。

没有人会放弃，您重新训练自己以识别更复杂的假货，并努力比伪造者领先一步。这个过程还在继续，伪造者不断更新他们的积木制造技术，同时你试图在拦截他们的假货方面变得越来越有成就！

每过一周，就越来越难区分真正的 Armo 积木和伪造的积木。经过数周改进后的锻造砖样品如图3.2 所示。

图3.2 锻造 Armo 砖样品

似乎这个简单的猫捉老鼠游戏足以推动伪造质量和检测质量的显着提高——现在让我们看看这与 GAN 的架构和训练过程有何关系！

GAN 简介

Armo Bricks and the Forgers 的故事描述了生成对抗网络 (GAN) 的训练过程。

GAN 是两个对手之间的战斗，生成器和鉴别器。生成器尝试将随机噪声转换为看起来好像是从原始数据集中采样的观察结果，而鉴别器则尝试预测观察结果是来自原始数据集还是生成器的伪造品之一。图3.3显示了两个网络的输入和输出示例。

图3.3 GAN 中两个网络的输入和输出

在过程开始时，生成器输出噪声图像，鉴别器随机预测。GAN 的关键在于我们如何交替训练两个网络，以便随着生成器变得更善于愚弄鉴别器，鉴别器必须适应以保持其正确识别哪些观察是假的能力。这驱使生成器寻找新的方法来愚弄鉴别器，如此循环下去。

深度卷积 GAN (DCGAN)

为了实际看到这一点，让我们开始在 Keras 中构建我们的第一个 GAN，以生成砖块图片。

此示例的代码包含在图书存储库的chapter05/gan/bricks/01_train.ipynb笔记本中。

准备数据

首先，您需要下载训练数据。我们将使用可通过 Kaggle 获得的乐高积木图像数据集。这是一个计算机渲染集合，包含从多个角度拍摄的 50 种不同乐高积木的 40,000 张摄影图像。

您可以通过运行图书存储库中的 Kaggle 数据集下载器脚本来下载数据集，如示例3-1 所示。这会将图像和附带的元数据本地保存到/data文件夹中。

示例 3-1 下载乐高积木数据集

bash scripts/download_kaggle_data.sh joosthazelzet lego-brick-images

我们使用 Keras 函数image_dataset_from_directory创建一个直接指向图像存储位置的 TensorFlow 数据集，如示例3-2所示。这允许我们仅在需要时（例如在训练期间）将成批图像读入内存，这样我们就可以处理大型数据集，而不必担心必须将整个数据集放入内存。它还将图像调整为 64x64，在像素值之间进行插值。

示例 3-2 预处理乐高积木数据集

train_data = image_dataset_from_directory(
    "/app/data/lego-brick-images/dataset/",
    labels=None,
    color_mode="grayscale",
    image_size=(64, 64),
    batch_size=128,
    shuffle=True,
    seed=42,
    interpolation="bilinear",
)

原始数据在 [0, 255] 范围内缩放以表示像素强度。在训练 GAN 时，我们将数据重新缩放到范围 [–1, 1]，这样我们就可以tanh在生成器的最后一层使用激活函数，它往往会提供比函数更强的梯度sigmoid。

示例 3-3 预处理乐高积木数据集

def preprocess(img):
    """
    Normalize and reshape the images
    """
    img = (tf.cast(img, "float32") - 127.5) / 127.5
    return img

train = train_data.map(lambda x: preprocess(x))

在整个示例中，将密切关注关于 GAN 的第一篇主要论文之一，“使用深度卷积生成对抗网络的无监督表示学习”。在这篇 2015 年的论文中，作者展示了如何构建深度卷积 GAN (DCGAN) 以从各种数据集生成逼真的图像。他们还对 GAN 的训练过程进行了一些更改，这些更改显着提高了生成图像的质量。

让我们先来看看我们是如何构建判别器的。

判别器

判别器的目标是预测图像是真实的还是假的。这是一个有监督的图像分类问题，因此我们可以使用与我们在 [Link to Come] 中看到的架构类似的架构：堆叠卷积层，具有单个输出节点。

我们将构建的鉴别器的完整架构如图3.4 所示。

图3.4 GAN的判别器

这示例3-4 中提供了构建鉴别器的 Keras 代码。

示例 3-4 判别器

discriminator_input = Input(shape=(64, 64, 1)) 
x = Conv2D(64, kernel_size=4, strides=2, padding="same", use_bias = False)(discriminator_input) 
x = LeakyReLU(0.2)(x)
x = Dropout(0.3)(x)
x = Conv2D(128, kernel_size=4, strides=2, padding="same", use_bias = False)(x)
x = BatchNormalization(momentum = 0.9)(x)
x = LeakyReLU(0.2)(x)
x = Dropout(0.3)(x)
x = Conv2D(256, kernel_size=4, strides=2, padding="same", use_bias = False)(x)
x = BatchNormalization(momentum = 0.9)(x)
x = LeakyReLU(0.2)(x)
x = Dropout(0.3)(x)
x = Conv2D(512, kernel_size=4, strides=2, padding="same", use_bias = False)(x)
x = BatchNormalization(momentum = 0.9)(x)
x = LeakyReLU(0.2)(x)
x = Dropout(0.3)(x)
x = Conv2D(1, kernel_size=4, strides=1, padding="valid", use_bias = False, activation = 'sigmoid')(x)
discriminator_output = Flatten()(x) 

discriminator = Model(discriminator_input, discriminator_output) 
discriminator.summary()

1.定义Input判别器（图像）。

2.Conv2D层层叠叠，层、BatchNormalization激活层LeakyReLU和Dropout层夹在中间。

3.展平最后一个卷积层——至此，张量的形状为 1x1x1，因此不需要最后一层Dense。

4.定义鉴别器的 Keras 模型——一种采用输入图像并输出 0 到 1 之间的单个数字的模型。

请注意我们如何在一些卷积层中使用步长 2 来减少张量通过网络时的空间形状（原始图像中为 64，然后是 32、16、8、4，最后是 1），同时增加在折叠为单个预测之前的通道数（灰度输入图像中为 1，然后是 64、128、256，最后是 512）。

我们在最后一层使用 sigmoid 激活Conv2D来输出 0 到 1 之间的数字。

生成器

现在让我们构建生成器。生成器的输入将是从多元标准正态分布中提取的向量。输出是与原始训练数据中的图像大小相同的图像。

此描述可能会让您想起变分自动编码器中的解码器。事实上，GAN 的生成器与 VAE 的解码器实现完全相同的目的：将潜在空间中的向量转换为图像。从潜在空间映射回原始域的概念在生成建模中非常普遍，因为它使我们能够操纵潜在空间中的向量来改变原始域中图像的高级特征。

我们将构建的生成器的架构如图3.5 所示。

图 3.5 生成器

示例3-5 中给出了构建生成器的代码。

示例 3-5 生成器

generator_input = Input(shape=(100,)) 
x = Reshape((1, 1, Z_DIM))(generator_input) 
x = Conv2DTranspose(512, kernel_size=4, strides=1, padding="valid", use_bias = False)(x) 
x = BatchNormalization(momentum=0.9)(x)
x = LeakyReLU(0.2)(x)
x = Conv2DTranspose(256, kernel_size=4, strides=2, padding="same", use_bias = False)(x)
x = BatchNormalization(momentum=0.9)(x)
x = LeakyReLU(0.2)(x)
x = Conv2DTranspose(128, kernel_size=4, strides=2, padding="same", use_bias = False)(x)
x = BatchNormalization(momentum=0.9)(x)
x = LeakyReLU(0.2)(x)
x = Conv2DTranspose(64, kernel_size=4, strides=2, padding="same", use_bias = False)(x)
x = BatchNormalization(momentum=0.9)(x)
x = LeakyReLU(0.2)(x)
generator_output = Conv2DTranspose(1, kernel_size=4, strides=2, padding="same", use_bias = False, activation = 'tanh')(x) 
generator = Model(generator_input, generator_output) 
generator.summary()

1.定义Input生成器——一个长度为 100 的向量。

2.我们使用Reshape层来给出 1 × 1 × 100 张量，这样我们就可以开始应用卷积转置操作。

3.我们通过四层传递它Conv2DTranspose，中间夹着BatchNormalization和层。LeakyReLU

4.最后一层Conv2DTranspose使用tanh激活函数将输出转换为范围 [–1, 1]，以匹配原始图像域。

5.定义生成器的 Keras 模型——接受长度为 100 的向量并输出形状为 的张量的模型[64, 64, 1]。

注意我们如何在某些层中使用 2 的步幅Conv2DTranspose来增加张量通过网络时的空间形状（原始向量中的 1，然后是 4、8、16、32，最后是 64），同时减少通道数（512，然后是 256、128、64，最后是 1 以匹配灰度输出）。

使用Conv2DTranspose层的另一种方法是使用UpSampling2D层，下一层Conv2D的步幅为 1，我们将在“上采样”中讨论。

上采样

使用的替代方法KerasConv2DTranspose层将改为使用一个UpSampling2D层，然后是步幅为 1 的普通层，如示例 3-6 Conv2D所示。

示例 3-6 上采样示例

x = UpSampling2D(size = 2)(x)
x = Conv2D(256, kernel_size=4, strides=1, padding="same")(x)

该UpSampling2D层简单地重复其输入的每一行和每一列，以便将大小加倍。然后步幅为 1 的层Conv2D执行卷积操作。它与卷积转置的想法类似，但不是用零填充像素之间的间隙，上采样只是重复现有的像素值。

两个都这些方法中的 - UpSampling2D+Conv2D和Conv2DTranspose- 是转换回原始图像域的可接受方法。这实际上是在您自己的问题设置中测试这两种方法并查看哪种方法产生更好结果的情况。已经证明该Conv2DTranspose方法可以导致输出图像中的伪影或小棋盘图案（参见图3.6 ）会破坏输出质量。然而，它们仍然在文献中许多最令人印象深刻的 GAN 中使用，并且已被证明是深度学习从业者工具箱中的强大工具——再次，我建议您尝试这两种方法，看看哪种方法最适合您。

图3.6 使用卷积转置层时的伪影

训练 DCGAN

作为我们已经看到，DCGAN 中生成器和鉴别器的架构非常简单，与我们之前看到的模型没有太大区别。理解 GAN 的关键在于理解判别器和生成器的训练过程。

我们可以通过创建一个训练集来训练鉴别器，其中一些图像是从训练集中随机选择的真实观察结果，一些是来自生成器的假输出。然后我们将其视为一个监督学习问题，其中真实图像的标签为 1，假图像的标签为 0，损失函数为二元交叉熵。

我们应该如何训练生成器？我们需要找到一种对每个生成的图像进行评分的方法，以便它可以针对高分图像进行优化。幸运的是，我们有鉴别器可以做到这一点！我们可以生成一批图像并将它们传递给鉴别器以获得每个图像的分数。生成器的损失函数就是这些概率和 1 向量之间的二元交叉熵，因为我们想训练生成器生成鉴别器认为真实的图像。

至关重要的是，我们必须交替训练这两个网络，确保我们一次只更新一个网络的权重。例如，在生成器训练过程中，只更新生成器的权重。如果我们也允许鉴别器权重发生变化，则鉴别器只会进行调整，以便更有可能预测生成的图像是真实的，这不是预期的结果。我们希望生成的图像被预测为接近 1（真实），因为生成器很强，而不是因为鉴别器很弱。

鉴别器和生成器的训练过程图如图3.7 所示。

图3.7 训练 DCGAN - 灰色框表示权重在训练过程中被冻结

Keras 为我们提供了创建自定义train_step函数以实现此逻辑的能力。示例 3-7 显示了该GAN模型，

示例 3-7 编译 DCGAN

class GAN(Model):
    def __init__(self, discriminator, generator, latent_dim):
        super(GAN, self).__init__()
        self.discriminator = discriminator
        self.generator = generator
        self.latent_dim = latent_dim

    def compile(self, d_optimizer, g_optimizer):
        super(GAN, self).compile()
        self.loss_fn = BinaryCrossentropy() 
        self.d_optimizer = d_optimizer
        self.g_optimizer = g_optimizer
        self.d_loss_metric = Mean(name="d_loss")
        self.g_loss_metric = Mean(name="g_loss")

    @property
    def metrics(self):
        return [self.d_loss_metric, self.g_loss_metric]

    def train_step(self, real_images):
        batch_size = tf.shape(real_images)[0]
        random_latent_vectors = tf.random.normal(shape=(batch_size, self.latent_dim)) 

        with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
            generated_images = self.generator(random_latent_vectors, training = True) 
            real_predictions = self.discriminator(real_images, training = True) 
            fake_predictions = self.discriminator(generated_images, training = True) 

            real_labels = tf.ones_like(real_predictions)
            real_noisy_labels = real_labels + NOISE_PARAM * tf.random.uniform(tf.shape(real_predictions))
            fake_labels = tf.zeros_like(fake_predictions)
            fake_noisy_labels = fake_labels - NOISE_PARAM * tf.random.uniform(tf.shape(fake_predictions))

            d_real_loss = self.loss_fn(real_noisy_labels, real_predictions)
            d_fake_loss = self.loss_fn(fake_noisy_labels, fake_predictions)
            d_loss = (d_real_loss + d_fake_loss) / 2.0 

            g_loss = self.loss_fn(real_labels, fake_predictions) 

        gradients_of_discriminator = disc_tape.gradient(d_loss, self.discriminator.trainable_variables)
        gradients_of_generator = gen_tape.gradient(g_loss, self.generator.trainable_variables)

        self.d_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables)) 
        self.g_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))

        self.d_loss_metric.update_state(d_loss)
        self.g_loss_metric.update_state(g_loss)

        return {m.name: m.result() for m in self.metrics}

gan = GAN(discriminator=discriminator, generator=generator, latent_dim=100)

gan.compile(
    d_optimizer=Adam(learning_rate=0.0002, beta_1 = 0.5, beta_2 = 0.999),
    g_optimizer=Adam(learning_rate=0.0002, beta_1 = 0.5, beta_2 = 0.999),
)

history = gan.fit(train, epochs=300)

1.生成器和判别器的损失函数为BinaryCrossentropy

2.要训练网络，首先从多元标准正态分布中抽取一批向量。

3.接下来，将它们传递给生成器以生成一批生成的图像。

4.现在让鉴别器预测这批真实图像的真实性……

5. 以及一批生成的图像。

6.鉴别器损失是真实图像（带有 label ）和假图像（带有 label ）的平均二元交叉熵0。

7.生成器损失是生成图像的鉴别器预测与 的标签之间的二元交叉熵1。

8.分别更新判别器和生成器的权重。

判别器和生成器不断争夺主导权，这使得 GAN 极难训练且不稳定。理想情况下，训练过程将找到一个平衡点，使生成器能够从鉴别器中学习到有意义的信息，并且图像质量将开始提高。经过足够多的 epoch 之后，判别器往往会占据主导地位，如图3.8 所示，但这可能不是问题，因为此时生成器可能已经学会了生成足够高质量的图像。

图 3.8 训练过程中判别器和生成器的损失和准确性

DCGAN分析

通过观察生成器在训练期间特定时期生成的图像（图3.9 ），很明显生成器越来越擅长生成本可以从训练集中提取的图像。

图 3.9 训练期间特定时期生成器的输出

神经网络能够将随机噪声转化为有意义的东西，这有点不可思议。值得记住的是，我们没有为模型提供除原始像素之外的任何其他功能，因此它必须完全自行制定高级概念，例如如何绘制阴影、长方体和圆形。

成功的生成模型的另一个要求是它不仅仅从训练集中再现图像。为了测试这一点，我们可以从训练集中找到最接近特定生成示例的图像。距离的一个很好的衡量标准是 L1 距离，定义为：

def compare_images(img1, img2):
    return np.mean(np.abs(img1 - img2))

图3.10 显示了训练集中最接近的观察结果，用于选择生成的图像。我们可以看到，虽然生成的图像和训练集之间存在一定程度的相似性，但它们并不完全相同。这表明生成器已经理解了这些高级特征，并且可以生成与它已经看到的不同的示例。.

图 3.10 从训练集中生成的图像的最接近匹配

GAN 挑战

尽管GAN 是生成建模的重大突破，但众所周知，它们很难训练。我们将探讨在本节中训练 GAN 时遇到的一些最常见的问题和挑战以及潜在的解决方案。在下一节中，我们将研究对 GAN 框架的一些更根本的调整，我们可以通过这些调整来解决其中的许多问题。

鉴别器压倒生成器

如果鉴别器变得太强，来自损失函数的信号就会变得太弱而无法驱动生成器进行任何有意义的改进。在最坏的情况下，鉴别器完美地学会了将真实图像与假图像分开，并且梯度完全消失，导致没有任何训练，如图 3.11 所示。

图3.11 鉴别器压倒生成器时的示例输出。

如果你发现你的判别器损失函数崩溃了，你需要找到削弱判别器的方法——试试下面的建议：

• 增加判别器中层的速率参数Dropout以抑制流经网络的信息量

• 降低判别器的学习率

• 减少鉴别器中卷积滤波器的数量

• 在训练鉴别器时向标签添加噪声（有关此示例，请参见示例 3-7 ）。

• 训练鉴别器时随机翻转一些图像的标签

生成器压倒鉴别器

如果鉴别器不够强大，生成器会想方设法用几乎相同图像的小样本轻松欺骗鉴别器。这被称为模式崩溃。

例如，假设我们在几个批次上训练生成器而不更新中间的鉴别器。生成器会倾向于找到一个总是愚弄鉴别器的单一观察（也称为模式），并开始将潜在输入空间中的每个点映射到该图像。此外，损失函数的梯度会崩溃到接近 0，因此无法从该状态恢复。

即使我们随后尝试重新训练鉴别器以阻止它被这一点所愚弄，生成器也会简单地找到另一种模式来愚弄鉴别器，因为它已经对其输入麻木了，因此没有动力使其输出多样化。

模式崩溃的影响可以在图3.12 中看到。

图 3.12 当生成器压倒鉴别器时模式崩溃的示例。

如果您发现您的生成器正在遭受模式崩溃，您可以尝试使用与上一节中列出的建议相反的建议来加强鉴别器。也可以尝试降低两个网络的学习率并增加批量大小。

无信息损失

自从深度学习模型被编译为最小化损失函数，很自然地认为生成器的损失函数越小，产生的图像质量越好。然而，由于生成器仅针对当前判别器进行评分并且判别器不断改进，因此我们无法比较训练过程中不同点评估的损失函数。事实上，在图3.8 中，生成器的损失函数实际上随着时间的推移而增加，即使图像质量明显提高。生成器损失和图像质量之间缺乏相关性有时会使 GAN 训练难以监控。

超参数

作为我们已经看到，即使是简单的 GAN，也有大量的超参数需要调整。除了判别器和生成器的整体架构外，还有控制批量归一化、丢弃、学习率、激活层、卷积过滤器、内核大小、步幅、批量大小和潜在空间大小的参数需要考虑。GAN 对所有这些参数的微小变化高度敏感，找到一组有效的参数通常是经过有根据的反复试验，而不是遵循一套既定的指导方针。

这就是为什么了解 GAN 的内部工作原理并知道如何解释损失函数很重要的原因——这样您就可以确定对超参数的合理调整，从而提高模型的稳定性。

应对 GAN 的挑战

近年来，几项关键进步极大地提高了 GAN 模型的整体稳定性，并降低了前面列出的一些问题的可能性，例如模式崩溃。

在本章的剩余部分中，我们将介绍 Wasserstein GAN with Gradient Penalty (WGAN-GP)，它对我们迄今为止探索的 GAN 框架进行了几个关键调整，以提高图像生成过程的稳定性和质量。

Wasserstein GAN - 梯度惩罚 (WGAN-GP)

在本节中，我们将构建一个 WGAN-GP，以从我们在第 4 章中看到的 CelebA 数据集生成人脸。

Wasserstein GAN (WGAN) 是稳定 GAN 训练的第一步。通过一些更改，作者能够展示如何训练具有以下两个属性的 GAN（引自论文）：

• 与生成器的收敛性和样本质量相关的有意义的损失指标

• 提高了优化过程的稳定性

具体来说，论文为判别器和生成器都引入了Wasserstein 损失函数。使用此损失函数而不是二元交叉熵可以使 GAN 收敛更稳定。

我们将首先定义 Wasserstein 损失函数，然后查看我们需要对模型网络和训练过程进行哪些其他更改以纳入我们的新损失函数。

Wasserstein 损失

让我们先让我们想起二元交叉熵损失——我们目前用来训练 GAN 的鉴别器和生成器的函数：

二元交叉熵损失

为了训练 GAN 判别器D，我们在将真实图像p i =D(x i )的预测与响应y i =1以及生成图像的预测p i =D(G(z i ))与响应y i = 0。因此对于GAN判别器，最小化损失函数可以写成：

GAN 鉴别器损失最小化

为了训练 GAN 生成器G ，我们在将生成图像p i =D(G(z i ))的预测与响应y i =1进行比较时计算损失。因此对于GAN生成器，最小化损失函数可以写成：

GAN 生成器损失最小化

现在让我们将其与 Wasserstein 损失函数进行比较。

首先，Wasserstein 损失要求我们使用y i =1和y i =-1作为标签，而不是 1 和 0。我们还从鉴别器的最后一层移除了 sigmoid 激活，这样预测p i不再是限制在[0,1]范围内，但现在可以是 [–∞, ∞] 范围内的任何数字。出于这个原因，WGAN 中的鉴别器通常被称为critic，它输出一个score而不是一个概率。

Wasserstein 损失函数定义如下：

Wasserstein 损失

为了训练 WGAN 评论家D，我们在比较真实图像p i =D(x i )的预测与响应y i =1和生成图像p i =D(G(z i ))的预测时计算损失响应y i = -1。因此对于 WGAN critic 来说，最小化损失函数可以写成：

WGAN 评论家损失最小化

换句话说，WGAN 评论家试图最大化其对真实图像和生成图像的预测之间的差异，真实图像得分更高。

为了训练 WGAN 生成器，我们在将生成图像p i =D(G(z i ))的预测与响应y i =1进行比较时计算损失。因此对于WGAN生成器，最小化损失函数可以写成：

WGAN 生成器损失最小化

Lipschitz 约束

它您可能会感到惊讶，我们现在允许 critic 输出 [–∞, ∞] 范围内的任何数字，而不是应用 sigmoid 函数将输出限制在通常的 [0, 1] 范围内。因此，Wasserstein 损失可能非常大，这令人不安——通常，神经网络中的大数字是要避免的！

事实上，WGAN 论文的作者表明，要使 Wasserstein 损失函数起作用，我们还需要对 critic 施加额外的约束。具体来说，要求critic是一个1-Lipschitz连续函数。让我们把它分开来更详细地理解它的含义。

评论家是将图像转换为预测的函数D。如果对于任意两个输入图像x 1和x 2满足以下不等式，我们就说这个函数是 1-Lipschitz ：

这里，x 1 – x 2是两幅图像之间的平均像素绝对差，并且|D(x1)-D(x2)|是评论家预测之间的绝对差异。本质上，我们需要限制 critic 的预测在两个图像之间变化的速率（即，梯度的绝对值必须在任何地方最多为 1）。我们可以在图3.13 中看到这适用于 Lipschitz 连续一维函数——无论您将圆锥放在线上的任何位置，直线都不会进入圆锥。换句话说，这条线在任何时候上升或下降的速度是有限制的。

图3.13 一个 Lipschitz 连续函数——存在一个双锥，无论它放在线上的哪个位置，函数总是完全位于锥之外

对于那些想要更深入地研究为什么 Wasserstein 损失仅在该约束为强制执行，Jonathan Hui 提供了一个很好的解释。

执行 Lipschitz 约束

在在最初的 WGAN 论文中，作者展示了如何在每个训练批次之后通过将 critic 的权重限制在一个小范围 [–0.01, 0.01] 内来强制执行 Lipschitz 约束。

对这种方法的批评之一是批评家的学习能力大大降低，因为我们正在削减它的权重。事实上，即使在原始的 WGAN 论文中作者写道，“权重剪裁显然是执行 Lipschitz 约束的糟糕方式。”。强有力的批评家对 WGAN 的成功至关重要，因为如果没有准确的梯度，生成器就无法学习如何调整其权重以产生更好的样本。

因此，其他研究人员一直在寻找替代方法来实施 Lipschitz 约束并提高 WGAN 学习复杂特征的能力。一种这样的方法称为 Wasserstein GAN-Gradient Penalty (WGAN-GP)。

在介绍这个变体的论文中，作者展示了如何通过在 critic 的损失函数中包含一个梯度惩罚项来直接强制执行 Lipschitz 约束，如果梯度范数偏离 1，它会对模型进行惩罚。这导致了一个更稳定的模型培训过程。

在下一节中，我们将看到如何将这个额外的项构建到我们的评论家的损失函数中。

梯度惩罚损失

图3.14 是示意图WGAN-GP 评论家的培训过程。如果我们将其与图3.7 中的原始鉴别器训练过程进行比较，我们可以看到关键的添加是作为整体损失函数的一部分的梯度惩罚损失，以及来自真实和假图像的 Wasserstein 损失。

图3.14 WGAN-GP critic 训练过程

梯度惩罚损失衡量输入图像的预测梯度范数与 1 之间的平方差。模型自然会倾向于找到确保梯度惩罚项最小化的权重，从而鼓励模型符合到 Lipschitz 约束。

在训练过程中到处计算这个梯度是很棘手的，所以 WGAN-GP 只在少数几个点上评估梯度。为了确保平衡的混合，我们使用一组插值图像，这些图像位于随机选择的点上，沿着将真实图像批次与伪造图像批次成对连接的直线，如图 3-15所示。

图 3.15 图像间插值

在示例3-8 中，我们展示了如何在代码中计算梯度惩罚

示例 3-8 梯度惩罚损失函数

def gradient_penalty(self, batch_size, real_images, fake_images):
    alpha = tf.random.normal([batch_size, 1, 1, 1], 0.0, 1.0) 
    diff = fake_images - real_images
    interpolated = real_images + alpha * diff 

    with tf.GradientTape() as gp_tape:
        gp_tape.watch(interpolated)
        pred = self.critic(interpolated, training=True) 

    grads = gp_tape.gradient(pred, [interpolated])[0] 
    norm = tf.sqrt(tf.reduce_sum(tf.square(grads), axis=[1, 2, 3])) 
    gp = tf.reduce_mean((norm - 1.0) ** 2) 
    return gp

1.批次中的每个图像都获得一个介于 0 和 1 之间的随机数，存储为向量alpha。

2.计算一组插值图像

3.评论家被要求对这些插值图像中的每一个进行评分

4.预测的梯度是根据输入图像计算的

5.计算该向量的 L2 范数

6.该函数返回 L2 范数与 1 之间的平均平方距离。

训练 WGAN-GP

使用 Wasserstein 损失函数的一个关键好处是我们不再需要担心平衡 critic 和 generator 的训练 - 事实上，当使用 Wasserstein 损失时，critic 必须在更新生成器之前训练到收敛，以确保生成器更新的梯度是准确的。这与标准 GAN 形成对比，在标准 GAN 中，重要的是不要让鉴别器变得太强，以避免梯度消失。

因此，对于 Wasserstein GAN，我们可以简单地在生成器更新之间对 critic 进行几次训练，以确保它接近收敛。使用的典型比率是每个生成器更新 3-5 个批评家更新。

我们现在已经介绍了 WGAN-GP 背后的两个关键概念——Wasserstein 损失和 critic 损失函数中包含的梯度惩罚项。示例3-9显示了包含所有这些想法的 WGAN 模型的训练步骤。您可以在书籍存储库的Jupyter 笔记本chapter05/wgan-gp/faces/train.ipynb中找到完整的模型类。

示例 3-9 训练 WGAN-GP

def train_step(self, real_images):
    batch_size = tf.shape(real_images)[0]

    for i in range(3): 
        random_latent_vectors = tf.random.normal(shape=(batch_size, self.latent_dim))

        with tf.GradientTape() as tape:
            fake_images = self.generator(random_latent_vectors, training = True)
            fake_predictions = self.critic(fake_images, training = True)
            real_predictions = self.critic(real_images, training = True)

            c_wass_loss = tf.reduce_mean(fake_predictions) - tf.reduce_mean(real_predictions) 
            c_gp = self.gradient_penalty(batch_size, real_images, fake_images)              c_loss = c_wass_loss + c_gp * self.gp_weight 

        c_gradient = tape.gradient(c_loss, self.critic.trainable_variables)
        self.c_optimizer.apply_gradients(zip(c_gradient, self.critic.trainable_variables)) 

    random_latent_vectors = tf.random.normal(shape=(batch_size, self.latent_dim))
    with tf.GradientTape() as tape:
        fake_images = self.generator(random_latent_vectors, training=True)
        fake_predictions = self.critic(fake_images, training=True)
        g_loss = -tf.reduce_mean(fake_predictions) 

    gen_gradient = tape.gradient(g_loss, self.generator.trainable_variables)
    self.g_optimizer.apply_gradients(
        zip(gen_gradient, self.generator.trainable_variables)
    ) 

    self.c_loss_metric.update_state(c_loss)
    self.c_wass_loss_metric.update_state(c_wass_loss)
    self.c_gp_metric.update_state(c_gp)
    self.g_loss_metric.update_state(g_loss)

    return {m.name: m.result() for m in self.metrics}

1.执行三个评论家更新。

2.计算评论家的 Wasserstein 损失——假图像和真实图像的平均预测之间的差异。

3.计算梯度惩罚项（参见示例3-8）。

4.critic 损失函数是 Wasserstein 损失和梯度惩罚的加权和

5.更新评论家的权重。

6.计算生成器的 Wasserstein 损失

7.更新生成器的权重。

WGAN-GP 中的批量归一化

一在构建 WGAN-GP 之前我们应该注意的最后一个考虑是批归一化不应该在评论中使用。这是因为批归一化在同一批次的图像之间建立了相关性，这使得梯度惩罚损失不太有效。实验表明，即使在 critic 中没有 batch normalization，WGAN-GPs 仍然可以产生出色的结果。

我们现在已经涵盖了标准 GAN 和 WGAN-GP 之间的所有主要区别。回顾一下：

• WGAN-GP 使用 Wasserstein 损失。

• WGAN-GP 使用标签 1 表示真实，-1 表示虚假进行训练。

• 评论家的最后一层没有 sigmoid 激活。

• 为生成器的每次更新多次训练评论家。

• critic 中没有批量归一化层。

• 在 critic 的损失函数中包含一个梯度惩罚项。

WGAN-GP分析

跑步书籍存储库中的Jupyter notebook chapter05/wgan-gp/faces/generate.ipynb将使用经过训练的模型生成新面孔。

首先，让我们看一下生成器的一些示例输出，经过 25 个 epoch 的训练（图3.16 ）。

图3.16 WGAN-GP CelebA 示例

很明显，该模型已经了解了人脸的重要高级属性，并且没有模式崩溃的迹象。

我们还可以看到模型的损失函数是如何随时间演变的（图3.17 ）——鉴别器和生成器的损失函数都非常稳定和收敛。

图3.17 WGAN-GP损失

如果我们将 WGAN-GP 输出与上一章的 VAE 输出进行比较，我们可以看到 GAN 图像通常更清晰——尤其是头发和背景之间的清晰度。总的来说是这样；VAE 倾向于生成模糊颜色边界的更柔和的图像，而已知 GAN 生成更清晰、更明确的图像。

的确，GAN 通常比 VAE 更难训练，并且需要更长的时间才能达到令人满意的质量。然而，当今大多数最先进的生成模型都是基于 GAN 的，因为在 GPU 上长时间训练大规模 GAN 的回报是巨大的。

Conditional GANs

到目前为止，在本章中，我们已经构建了能够从给定训练集中生成逼真的图像的 GAN。然而，我们无法控制我们想要生成的图像类型——例如，男性或女性的脸，或者大砖块或小砖块。我们可以从潜在空间中采样一个随机点，但我们无法轻松理解在选择潜在变量的情况下会产生什么样的图像。

在本章的最后一部分，我们将把注意力转向构建一个我们能够控制输出的 GAN——所谓的条件 GAN，或 CGAN。这个想法首先被引入到 Mirza 等人的 Conditional Generative Adversarial Nets 论文中。7并且是对 GAN 架构的一个相对简单的扩展。我们将把相同的核心思想应用于我们在本章前一节中已经看到的 WGAN-GP 架构。

CGAN架构

在这个例子中，我们将根据人脸数据集的金发属性来调节我们的 CGAN。也就是说，我们将能够明确指定我们是否喜欢生成金色头发的图像。此标签作为 CelebA 数据集的一部分提供。

高级 CGAN 架构如图3-18所示：

图 3.18 CGAN 中生成器和评价器的输入和输出

标准 GAN 和 CGAN 之间的主要区别在于，在 CGAN 中，我们将额外的信息传递给与标签相关的生成器和评论家。在生成器中，这只是作为一个单热编码向量附加到潜在空间样本中。在评论家（或鉴别器，如果使用标准 GAN）中，我们将标签信息作为额外通道添加到 RGB 图像中。我们通过重复 one-hot 编码向量来填充与输入图像相同的形状来做到这一点。

在我们的示例中，我们的 one-hot 编码标签的长度为 2，因为有两个类别（金发/非金发）。但是，您可以拥有任意数量的标签——例如，您可以在时尚 MNIST 数据集上训练 CGAN 以输出十种不同时尚商品中的一种，方法是将长度为 10 的单热编码标签向量合并到输入中生成器和 10 个额外的单热编码标签通道进入评论家的输入。

因此，我们需要对架构进行的唯一更改是生成器和评论家的输入形状，如示例3-10 所示。

示例 3-10 CGAN 中的输入层

critic_input = Input(shape=(64, 64, 3)) 
label_input = Input(shape=(64, 64, 2))
x = Concatenate(axis = -1)([critic_input, label_input])
...
generator_input = Input(shape=(32,)) 
label_input = Input(shape=(2,))
x = Concatenate(axis = -1)([generator_input, label_input])
x = Reshape((1,1, 32 + 2))(x)
...

1.图像通道 (3) 和标签通道 (2) 分别传递给评论家并连接 (5)。

2.潜在向量 (32) 和标签类 (2) 分别传递给生成器并在重塑之前连接起来。

训练 CGAN

我们还必须对 CGAN 的 进行一些更改，以匹配生成器和评论家的新输入格式，如示例3-11 train_step所示。

示例 3-11 CGAN 的 train_step

def train_step(self, data):
    real_images, one_hot_labels = data 

    image_one_hot_labels = one_hot_labels[:, None, None, :] 
    image_one_hot_labels = tf.repeat(image_one_hot_labels, repeats=IMAGE_SIZE, axis = 1)
    image_one_hot_labels = tf.repeat(image_one_hot_labels, repeats=IMAGE_SIZE, axis = 2)

    batch_size = tf.shape(real_images)[0]

    for i in range(self.critic_steps):
        random_latent_vectors = tf.random.normal(shape=(batch_size, self.latent_dim))

        with tf.GradientTape() as tape:
            fake_images = self.generator([random_latent_vectors, one_hot_labels], training = True) 

            fake_predictions = self.critic([fake_images, image_one_hot_labels], training = True) 
            real_predictions = self.critic([real_images, image_one_hot_labels], training = True)

            c_wass_loss = tf.reduce_mean(fake_predictions) - tf.reduce_mean(real_predictions)
            c_gp = self.gradient_penalty(batch_size, real_images, fake_images, image_one_hot_labels) 
            c_loss = c_wass_loss + c_gp * self.gp_weight

        c_gradient = tape.gradient(c_loss, self.critic.trainable_variables)
        self.c_optimizer.apply_gradients(zip(c_gradient, self.critic.trainable_variables))

    random_latent_vectors = tf.random.normal(shape=(batch_size, self.latent_dim))

    with tf.GradientTape() as tape:
        fake_images = self.generator([random_latent_vectors, one_hot_labels], training=True) 
        fake_predictions = self.critic([fake_images, image_one_hot_labels], training=True)
        g_loss = -tf.reduce_mean(fake_predictions)

    gen_gradient = tape.gradient(g_loss, self.generator.trainable_variables)
    self.g_optimizer.apply_gradients(
        zip(gen_gradient, self.generator.trainable_variables)
    )

1.图像和标签从输入数据中解包。

2.one-hot 编码向量被扩展为与输入图像大小相同的 one-hot 编码图像。

3.现在向生成器提供两个输入的列表——随机潜在向量和单热编码标签向量。

4.现在，评论家收到了一份包含两个输入的列表——假/真图像和单热编码标签通道。

5.梯度惩罚函数在使用 critic 时还需要通过 one-hot-encoded 标签通道。

6.对 critic 训练步骤所做的更改也适用于生成器训练步骤。

CGAN分析

CGAN 之所以起作用，是因为评论家现在可以访问有关图像内容的额外信息，因此生成器必须注意这一点，以便继续愚弄评论家。例如，如果生成器生成了与图像标签不一致的完美图像，评论家仍然会知道它们是假的——不是因为图像质量差，而是因为图像和标签不匹配。

因此，生成器必须注意作为输入传递的标签，并确保它输出与标签匹配的图像，以愚弄评论家。

我们可以通过将特定的单热编码标签传入生成器的输入来控制 CGAN 的输出。例如，要生成一张非金色头发的脸，我们传入向量[1, 0]。为了生成一张金色头发的脸，我们传入了向量[0, 1]。

CGAN 的输出如图3.19 所示。在这里，我们在示例中保持随机潜在向量相同，并仅更改条件标签向量。很明显，CGAN 已经学会了使用标签向量来仅控制图像的头发颜色属性。令人印象深刻的是，图像的其余部分几乎没有变化——这证明了 GAN 能够以这样一种方式组织潜在空间中的点，使得各个特征可以相互解耦。

图3.19 当Blonde和Not Blonde向量附加到潜在样本时，CGAN 的输出。

如果标签可用于您的数据集，将它们作为 GAN 的输入通常是一个好主意，即使您不一定需要在标签上调节生成的输出，因为它们往往会提高生成图像的质量。您可以将标签视为对像素输入的高度信息扩展。

概括

在本章中，我们探索了三种不同的 GAN 模型——DCGAN、更复杂的 WGAN-GP 和 CGAN。

所有 GAN 的特征都是生成器与鉴别器（或批评器）架构，鉴别器试图“发现”真实图像和假图像之间的差异，而生成器旨在愚弄鉴别器。通过平衡这两个对手的训练方式，GAN 生成器可以逐渐学习如何产生与训练集中相似的观察结果。

我们首先看到了如何训练深度卷积 GAN (DCGAN) 以从公开可用的数据集中生成砖块图像。它能够学习如何将 3D 对象逼真地表示为图像，包括阴影、形状和纹理的准确表示。

然后，我们探讨了 GAN 训练可能失败的不同方式，包括模式崩溃和梯度消失，以及 Wasserstein 损失函数如何解决其中的许多问题并使 GAN 训练更具可预测性和可靠性。WGAN-GP 将 1-Lipschitz 要求置于训练过程的核心，方法是在损失函数中包含一个项以将梯度范数拉向 1。

我们将 WGAN-GP 应用于人脸生成问题，并了解如何通过简单地从标准正态分布中选择点来生成新的人脸。这个采样过程与 VAE 非常相似，尽管 GAN 生成的人脸非常不同——通常更清晰，图像不同部分之间的区别更大。当在强大的 GPU 上进行训练时，这一特性使 GAN 能够产生极其令人印象深刻的结果，并将生成建模领域推向了前所未有的高度。

最后，我们构建了一个条件 GAN 或 CGAN，它允许我们控制生成的图像类型。它的工作原理是将标签作为输入传递给评论家和生成器，从而为网络提供所需的额外信息，以便在给定标签上调节生成的输出。

总的来说，我们已经看到 GAN 框架是如何极其灵活并且能够适应许多有趣的问题领域的。