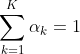EM算法在二维高斯混合模型参数估计中的应用

• 高斯混合模型

高斯混合模型是指具有如下形式的概率分布模型：

其中，是系数，，；是高斯分布密度，，

称为第k个分模型。

参考：《统计学习方法》9.3 EM算法在高斯混合模型学习中的应用

• 多维高斯混合模型

多维高斯混合模型具有如下形式的概率分布模型：

其中d为数据的维度，为均值，为协方差矩阵。

对于二维高斯混合模型，d=2，y和都是二维的数据，用矩阵表示就是一行两列，则是两行两列的协方差矩阵。

• 二维高斯混合模型参数估计的EM算法

输入：观测数据，二维高斯混合模型；

输出：二维高斯混合模型参数。

算法步骤如下：

（1）取参数的初始值开始迭代

（2）E步：依据当前模型参数，计算分模型k对观测数据的响应度：

（3）M步：计算新一轮迭代的模型参数：

（4）重复第(2)步和第(3)步，直到收敛。

• 实验步骤

1.确定二维高斯混合模型的参数

我们的二维高斯混合模型为两个权重不同的二维单高斯分布组合而成，所以可以简化为一个参数，即第一个二维单高斯分布的权重为π，第二个二维单高斯分布的权重为1-π。选择π值为0.8，第一个二维单高斯分布的均值为，协方差矩阵为，第二个二维单高斯分布的均值为，协方差矩阵为。

import numpy as np
import matplotlib.pyplot as plt


N = 1000
pi = 0.8
mean_1 = np.array([0.0, 0.0])
cov_1 = np.mat([[1.0, 0.0], [0.0, 1.0]])
mean_2 = np.array([3.0, 3.0])
cov_2 = np.mat([[1.0, 0.5], [0.5, 1.0]])


class GMM:
    def __init__(self, N, pi, mean_1, cov_1, mean_2, cov_2):
        # 采样点数
        self.N = N
        # 高斯分布的权重
        self.pi = pi
        # 第一个二维高斯分布的均值
        self.mean_1 = mean_1
        # 第一个二维高斯分布的协方差矩阵
        self.cov_1 = cov_1
        # 第二个二维高斯分布的均值
        self.mean_2 = mean_2
        # 第二个二维高斯分布的协方差矩阵
        self.cov_2 = cov_2

 该二维高斯混合模型的大致图像如下：

 2.采样

选取采样点为1000个。采样方法为在1000次循环中，每次产生一个0-1的随机数，如果小于0.8，则以第一个二维单高斯分布的概率密度函数生成一个样本点；如果大于0.8，则以第二个二维单高斯分布的概率密度函数生成一个样本点，最后以生成的1000个样本点作为观测数据集。

# 生成观测数据集
def dataset(self):
    # 数据集大小为(N,2)
    D = np.zeros(shape=(self.N, 2))
    for i in range(self.N):
        # 产生0-1之间的随机数
        j = np.random.random()
        if j < self.pi:
            # pi的概率以第一个二维高斯分布产生一个样本点
            x = np.random.multivariate_normal(mean=self.mean_1, cov=self.cov_1, size=1)
        else:
            # 1-pi的概率以第二个二维高斯分布产生一个样本点
            x = np.random.multivariate_normal(mean=self.mean_2, cov=self.cov_2, size=1)
        D[i] = x
    return D

 生成的观测数据集的分布图如下：

gmm = GMM(N, pi, mean_1, cov_1, mean_2, cov_2)
plt.figure()
plt.gca().set_aspect('equal')  # 令x轴和y轴的同一区间的刻度相同
D = gmm.dataset()
plt.scatter(D[:, 0], D[:, 1])
plt.show()

3.利用EM算法进行参数估计

（1）参数初始化

选取参数的初始值为π为0.5，第一个均值为，第一个协方差矩阵为，第二个均值为，第二个协方差矩阵为。

def EM(self, D, N):
    p = 0.5
    m_1 = np.array([[0.0, 0.0]])
    c_1 = np.mat([[1.0, 0.0], [0.0, 1.0]])
    m_2 = np.array([[1.0, 1.0]])
    c_2 = np.mat([[1.0, 0.0], [0.0, 1.0]])

（2）E步

依据当前模型参数，计算分模型k对观测数据的响应度，由于该模型只有两个二维单高斯分布组成，故K=2：

其中的表达式为：

    # 高斯分布密度phi
    def phi(x, mean, cov):
        return np.exp(-(x - mean) * np.linalg.pinv(cov) * (x - mean).T / 2) /
                (2 * np.pi * np.sqrt(np.linalg.det(cov)))

    # 分模型对观测数据的响应度gamma
    def gamma(D, j, k, p, m_1, c_1, m_2, c_2):
        # 第一个分模型
        if k == 0:
            return p * phi(D[j], m_1, c_1) / (p * phi(D[j], m_1, c_1) + (1 - p) * phi(D[j], m_2, c_2))
        # 第二个分模型
        elif k == 1:
            return (1 - p) * phi(D[j], m_2, c_2) / (p * phi(D[j], m_1, c_1) + (1 - p) * phi(D[j], m_2, c_2))

（3）M步

计算新一轮迭代的模型参数：

    def mu(D, g, N):
        # 第一个分模型的均值的分子部分
        mu_1a = np.array([[0.0, 0.0]])
        # 第一个分模型的均值的分母部分
        mu_1b = np.array([[0.0, 0.0]])
        # 第二个分模型的均值的分子部分
        mu_2a = np.array([[0.0, 0.0]])
        # 第二个分模型的均值的分母部分
        mu_2b = np.array([[0.0, 0.0]])
        for j in range(N):
            mu_1a += g[j][0] * D[j]
            mu_1b += g[j][0]
            mu_2a += g[j][1] * D[j]
            mu_2b += g[j][1]
        # 返回第一个分模型的均值和第二个分模型的均值，都是一行两列的矩阵
        return mu_1a / mu_1b, mu_2a / mu_2b

    # 模型的协方差矩阵sigma
    def sigma(D, m1, m2, g, N):
        # 第一个分模型的协方差矩阵的分子部分
        sigma_1a = np.mat([[0.0, 0.0], [0.0, 0.0]])
        # 第一个分模型的协方差矩阵的分母部分
        sigma_1b = np.mat([[0.0, 0.0], [0.0, 0.0]])
        # 第二个分模型的协方差矩阵的分子部分
        sigma_2a = np.mat([[0.0, 0.0], [0.0, 0.0]])
        # 第二个分模型的协方差矩阵的分母部分
        sigma_2b = np.mat([[0.0, 0.0], [0.0, 0.0]])
        for j in range(N):
            sigma_1a += g[j][0] * ((D[j] - m1).T * (D[j] - m1))
            sigma_1b += g[j][0]
            sigma_2a += g[j][1] * ((D[j] - m2).T * (D[j] - m2))
            sigma_2b += g[j][1]
        # 返回第一个分模型的协方差矩阵和第二个分模型的协方差矩阵，都是两行两列的矩阵
        return sigma_1a / sigma_1b, sigma_2a / sigma_2b

由于该模型只有两个二维单高斯分布组成，故只需要求第一个分模型的权重π，第二个分模型的权重1-π即可得到。

即只需要求下式：

    # 模型的权重alpha
    def alpha(g, N):
        a = 0
        for j in range(N):
            # 只需要求第一个分模型的权重
            a += g[j][0]
        return a / N

（4）重复第2步和第3步，直到收敛

标准做法是重复以上计算，直到对数似然函数值不再有明显变化为止。这里为了计算方便，当权重π的变化量小于时，停止迭代。

    # 权重pi的变化量初始化为1
    delta_p = 1
    # 迭代次数i
    i = 0
    # 当权重pi的变化量小于10e-7时停止迭代
    while delta_p > 10e-7:
        Gamma = np.zeros(shape=(N, 2))
        for j in range(N):
            for k in range(2):
                # 计算分模型k对观测数据的响应度gamma
                Gamma[j][k] = gamma(D, j, k, p, m_1, c_1, m_2, c_2)
            
        # 更新模型的均值
        m_1, m_2 = mu(D, Gamma, N)
        # 更新模型的协方差矩阵
        c_1, c_2 = sigma(D, m_1, m_2, Gamma, N)
        # 计算权重pi的变化量
        delta_p = abs(p - alpha(Gamma, N))
        # 更新模型的权重
        p = alpha(Gamma, N)

        i += 1
        # 每五次迭代打印权重值
        if i % 5 == 0:
            print(i, "steps' pi:", p)

返回EM算法得到的五个参数值、

    # 返回EM算法学习到的五个参数
    return p, m_1, c_1, m_2, c_2

4.将学习到的参数与设定值比较

pi_learn, mean_1_learn, cov_1_learn, mean_2_learn, cov_2_learn = gmm.EM(D, N)
print("权重值：", pi_learn)
print("第一个分模型的均值：\n", mean_1_learn)
print("第一个分模型的协方差矩阵：\n", cov_1_learn)
print("第二个分模型的均值：\n", mean_2_learn)
print("第二个分模型的协方差矩阵：\n", cov_2_learn)

50 steps' pi: 0.7930182035003274
权重值： 0.7930182035003274
第一个分模型的均值： 
[[-0.08556625 -0.03833228]]
第一个分模型的协方差矩阵： 
[[ 0.97774587 -0.04718663]
 [-0.04718663  0.88868208]]
第二个分模型的均值： 
[[2.89290133 3.01754719]]
第二个分模型的协方差矩阵： 
[[1.06842288 0.45923016]
 [0.45923016 0.93972666]]

经过50次迭代后停止学习，50 steps' pi: 0.7930182035003274

得到权重值π为0.7930182035003274

第一个二维单高斯分布的均值为[[-0.08556625 -0.03833228]]

协方差矩阵为

[[ 0.97774587 -0.04718663]
 [-0.04718663  0.88868208]]

第二个二维单高斯分布的均值为[[2.89290133 3.01754719]]

协方差矩阵为

[[1.06842288 0.45923016]
 [0.45923016 0.93972666]]

可以看到，EM算法学习到的二维高斯混合模型的参数接近于设定值。

• 考虑采样点数N对参数估计的影响

比较N取100,1000,10000时参数估计的准确度，由于一次参数估计的随机性太大，故不同的N值各进行10次参数估计并计算权重值π的均值和方差。

# 计算steps次参数估计的权重值的均值和方差
def pi_N(N, pi, mean_1, cov_1, mean_2, cov_2, steps):
    gmm = GMM(N, pi, mean_1, cov_1, mean_2, cov_2)
    pi_steps = np.zeros(shape=steps)
    # 均值
    pi_mu = 0
    # 方差
    pi_sigma = 0

    # 计算steps次估计值和均值
    for i in range(steps):
        D = gmm.dataset()
        pi_learn, _, _, _, _ = gmm.EM(D, N)
        pi_mu += pi_learn
        pi_steps[i] = pi_learn

    pi_mu /= steps

    # 计算steps次方差
    for i in range(steps):
        pi_sigma += (pi_steps[i]-pi_mu)**2

    pi_sigma /= steps

    return pi_mu, pi_sigma

（1）取N=100

# 参数估计次数steps
steps = 10

Y_mu = []
Y_sigma = []

pi_mu_100, pi_sigma_100 = pi_N(N1, pi, mean_1, cov_1, mean_2, cov_2, steps)
Y_mu.append(pi_mu_100)
Y_sigma.append(pi_sigma_100)
print("N=100时学习", steps, "次得到的权重值均值：", pi_mu_100, ",方差：", pi_sigma_100)

N=100时学习 10 次得到的权重值均值： 0.7482191862720133 ,方差： 0.0024508318225135105

（2）取N=1000

pi_mu_1000, pi_sigma_1000 = pi_N(N2, pi, mean_1, cov_1, mean_2, cov_2, steps)
Y_mu.append(pi_mu_1000)
Y_sigma.append(pi_sigma_1000)
print("N=1000时学习", steps, "次得到的权重值均值：", pi_mu_1000, ",方差：", pi_sigma_1000)

N=1000时学习 10 次得到的权重值均值： 0.8033618327297114 ,方差： 0.0001821331641820217

（3）取N=10000

pi_mu_10000, pi_sigma_10000 = pi_N(N3, pi, mean_1, cov_1, mean_2, cov_2, steps)
Y_mu.append(pi_mu_10000)
Y_sigma.append(pi_sigma_10000)
print("N=10000时学习", steps, "次得到的权重值均值：", pi_mu_10000, ",方差：", pi_sigma_10000)

N=10000时学习 10 次得到的权重值均值： 0.7980447763980503 ,方差： 1.5680138676242733e-05

 

将不同的N值所学习到的权重值的均值与设定值(0.8)相比较，并画在柱状图中，可以看到N越大，其学习到的权重值的均值越接近于设定值0.8。

Y_mu.append(0.8)
X = [1, 2, 3, 4]
plt.bar(X, Y_mu, align='center', tick_label=['N=100', 'N=1000', 'N=10000', 'standard value'], width=0.5)
plt.ylim((0.77, 0.82))
plt.xlabel('different N')
plt.ylabel('mean of pi')
plt.show()

由于N=10000时方差接近为0，不方便画图，从数据上直观来看，N越大，其学习到的权重值的方差越小且接近于0.

总体上来说，样本点数N取的越大，使用EM算法学习高斯混合模型的参数效果越好。