链表(一)

在开始内容前,我们先来聊聊链表是什么,以及它的优点(我们到底为什么要创建出链表这一种数据结构呢)

1. 在刚开始的c语言学习中,我们可以知道储存数据时我们一般用到的都是数组,但当我们要储存复杂的且不知道确切数量的数据,并且还需要频繁的插入和删除数据时,用数组总觉得有些束手束脚,因此,链表诞生了
2. 链表是动态使用内存,即用即申请,可以更好的利用空间,而不会浪费
3. 正因为它是动态数据结构,因此申请的内存不一定像数组那样是连续的,就需要指针来定位我们申请到的空间,将它类似的变成数组那样的线性结构(即我们能通过当前的空间找到下一个空间,因此该指针需要储存下一个空间的地址)
4. 因为我们每一个空间都需要存储数据和地址,所以我们定义一个结构体来储存这样不同类型的数据,以结构体的大小来申请空间

好了,开始我们的正式内容! 

(要记得!!!看不懂代码的时候,一定要跟着我对代码的解释画图或者看代码直接画图,可以加深理解)

先来最基础的单向链表

1.创建

前面我们已经提到了用结构体来申请空间,因此我们先创建一个结构体

我们需要定义两种类型的数据,你输入的数据和地址(我们这里默认输入int)

typedef struct node {
	int data;
	struct node* next;
}node;

node就是我们的结构体类型(因为我使用了typedef,可以自定义名字,node代替了struct node来使用)

 2.初始化

创建之后我们就需要定义结构体指针以及初始化指针

node* head, * new, * perious, * t,*p;
	head = NULL;
	head = (node*)malloc(sizeof(node));
	head->next = NULL;
	new = NULL;perious = NULL;p = NULL;t = head;

 我们将每一块申请的空间称之为结点,将我们用指针连接的一串空间称为链表

结点中的两种数据类型分别叫数据域和指针域(听起来是不是很高大上,但其实也就是那么回事)

1. head就是我们的头指针,它申请了空间,因此成为了我们的头结点(这里我们不在头结点中存放数据,方便后续的插入)
2. new是我们之后申请的新结点,perious是我们的上一个结点,在后续操作会用到
3. t和p是我们的工具人工具结点,方便各种操作
4. head->next就是我们存放 头结点指向下一个结点地址 的地方

我们先将定义的指针赋初值,我使用的是vs,vs太安全了,不初始化不能运行(不要忘记head->next喔)

我们这里的每一块代码都可以定义为一个函数(我当时写单向链表时没注意这个,就没写,但之后的循环和双向链表我都写啦,可以看那个作为参考,其实也就是把head传进去就行,没啥好参考的)

 3.插入

插入就是我们每一次输入数据的过程

我们一般分为两种方式,尾插法和头插法(我们这里介绍3种)

//尾插法
	int n = 0;
	scanf("%d", &n);
	int a = 0,i = 0;
	for (i = 0; i < n; i++) {
		new = (node*)malloc(sizeof(node));
		scanf("%d", &a);
		new->data = a;
		new->next = NULL;
		t->next = new;
		t = new;
	}
	t->next = NULL;

插入过程的结束可以有两种方式,自己先定义数量和手动停止(当输入数据为0时停止)

这里是第一种方法,方法二用while(1)+break实现

具体过程就是:

1. 先为你要使用的结点申请空间,malloc函数可以实现该操作
2. 前括号内需要该数据类型的指针(因为我们定义的是结构体指针,即node*)
3. 后括号为申请空间的大小(我们前面提过,结点的大小由结构体决定,因此为sizeof(node))
4. node是我们结构体类型
5. 将输入的a存入新结点的数据域中(用->来访问结构体中的成员喔,因为new是指针捏)
6. 还记得我们小小工具人t吗,我们之前初始化的时候把它初始化为头结点了(为了使真正的头结点不变捏),我们将new的地址存放在t中,就可以把t和new连接起来了
7. 最后将t指向new,就表示t向后移动了一个结点,当我们进行第二次循环时,此时的t就是第二个结点了,重复上述操作,我们就将第二个和第三个结点连接起来,t也挪到第三个结点的位置.....

重复上述操作,我们就实现了将输入的数据从该链表的尾部插入并连接,这样当我们从头结点遍历时,输出数据的顺序和输入顺序一样

出循环后,不要忘记将最后一个结点指向的空间赋初值喔!!!否则它就变成野指针啦!(变成野指针时,我们对最后一个结点的next访问时就会出现问题,至于我们为什么要访问最后一个结点的next,当然是因为我们遍历结束的条件就是检测该结点的next是否为NULL,也就是我们赋的初值)

//头插法
	t = head;
	while (1) {
		int m = 0;
		scanf("%d", &m);
		if (m == 0) {
			break;
		}
		else {
			new = (node*)malloc(sizeof(node));
			new->data = m;
			new->next= t->next;
			t->next = new;
		}
	}

这里头插法的循环就用到了上文提到的方法二(while)

因为其他的在尾插法已经介绍的很详细了,这里就只说一下核心

1. 还是我们眼熟的工具人t,它现在是头结点,因为我们现在还没有和新结点相连,因此t->next是NULL,那么这里就是将new->next赋NULL,再将new与t相连
2. 第二次循环时,先将new与刚刚建立的结点相连,再将new与t相连,这样我们就实现了在头结点和第二个结点之间插入一个新结点
3. 重复上述操作,就是不断的将新结点放在头结点之后,因此输出的顺序与是输入顺序的倒序
4. 因为我们的新结点都是指向第二个结点,而在建立第二个结点时,我们已经赋了初值,,因此最后不需要赋NULL

这里我们再介绍一种插入(按大小顺序插入)

//插入(已有一段序列,按大小顺序插入)
	int m = 0;
	printf("\n");
	scanf("%d", &m);
	t = head;
	while (t != NULL) {
			if (t->next->data >= m) {
				p = (node*)malloc(sizeof(node));
				p->data = m;
				p->next = t->next;
				t->next = p;
				break;
			}
			else {
				if (t->next->next == NULL) {
					p = (node*)malloc(sizeof(node));
                    p->data = m;
					(t->next)->next = p;
					p->next = NULL;
					break;
				}
				else {
					p = (node*)malloc(sizeof(node));
					p->data = m;
					p->next = (t->next)->next;
					(t->next)->next = p;
					break;
				}
			}
			t = t->next;
	}

需要配合头插法和尾插法使用哈,我们得先有一串链表

当输入的数小于等于结点的数据时,就放在该结点的前面;大于时,就放在后面

1. 从前面插入时,不需要其他的判断,插入方式和头插法类似
2. 但要注意!从后面插入时,要判断t后面的后面是否为NULL,因为两种情况的处理方式不同

• 如果不为NULL,方法和前插类似,只是插入的地方向后了一个结点
• 若为NULL,和尾插法类似

这里我只设置了输入一个数字,你也可以外加一个循环:

//插入(已有一段序列,按大小顺序插入)
	int m = 0;
	printf("\n");
	scanf("%d", &m);
	while (m != 0) {
		t = head;
		while (t != NULL) {
			if (t->next->data >= m) {
				p = (node*)malloc(sizeof(node));
				p->data = m;
				p->next = t->next;
				t->next = p;
				break;
			}
			else {
				if (t->next->next == NULL) {
					p = (node*)malloc(sizeof(node));
					(t->next)->next = p;
					p->next = NULL;
					break;
				}
				else {
					p = (node*)malloc(sizeof(node));
					p->data = m;
					p->next = (t->next)->next;
					(t->next)->next = p;
					break;
				}
			}
			t = t->next;
		}
		scanf("%d", &m);
	}

区别不大

如果先前的链表本身就有序,且你只插入一个,还是有用的

但在第二张图就有漏洞了,不能保证有序插入,应该还能再改改(不过那样就好麻烦,放弃惹) 

 4.删除

//删除
	printf("请输入你要删除数字的序号:");
	int m = 0,j=0;
	scanf("%d", &m);
	node* q;
	p = head;
	while (j < m - 1 && p != NULL) {
		j++;
		p = p->next;
	}
	if (p == NULL || p->next == NULL) {
		printf("不存在\n");
	}
	else {
		q = p->next;
		p->next = q->next;
		free(q);
	}

当我们输入该序号后,我们通过循环来找到该结点的前一个结点,因为我们的删除操作就是绕过删除的结点,再将该结点释放

因此,如何实现绕过该结点呢,就是找到该结点的前一个结点,将其与该结点的下一个结点相连

但我们也要判断一下输入的序号是否合法,我们的p如果是NULL或者要删除的结点(p->next)为NULL,需要进行输出,用来提醒我们(不然出现错误咱还不知道哪错了呢)

5.查找

//查找
	p = head->next;
	printf("请输入你要查找的数字:");
	int m = 0;
	scanf("%d", &m);
	while (p != NULL) {
		if (p->data == m) {
			printf("找到了\n");
			printf("%d", p->data);
			return 0;
		}
		p = p->next;
	}
	if (p == NULL) {
		printf("不存在\n");
	}

当我们没有找到的时候,p指针向后挪;

找到了就提示一下我们,并将其打印出来,视觉效果更好=)

(记得找到了就直接退出去,不然当你找的是最后一个结点的数据时,出循环后p此时就是NULL了)

要是遍历完链表后仍没有找到,就提示我们该数据不存在

6.遍历打印

t = head->next;
	while (t != NULL) {
		printf("%d ", t->data);
		t = t->next;
	}

简洁明了,咱不说也能明白的

7.统计当前结点个数

//统计结点个数
	p = head->next;
	int count = 0;
	while (p != NULL) {
		count++;
		p = p->next;
	}
	printf("%d", count);

就是定义一个统计的变量,和遍历的操作一样

 8.逆置链表

void reverse(node* head) {
	node* p, * q;
	p = head->next;
	head->next = NULL;
	while (p) {
		q = p->next;
		p->next = head->next;
		head->next = p;
		p = q;
	}
}

上述代码是在已经有一串链表的前提下写的

让我们的小小工具人p=头结点之后的第一个结点,之后将head的指针域赋空,因此先前的链表已经没有头结点惹

接下来就是逆置的过程啦!!请准备好纸笔,跟着我一起画图=)   

(我个人当时学的时候干看代码还是很吃力的,画图救了我狗命)

(纸上画不太好演示,我就用画图软件示例啦)

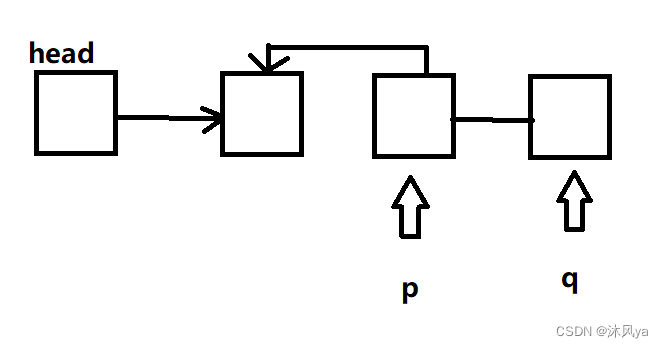
先画一个单拎出来的头结点(标为head),再画一串从p开始的链表

此时,q为p的下一个结点,标记上哟

 因为此时head指向空,因此p也指向NULL(记得和代码对照哟!)

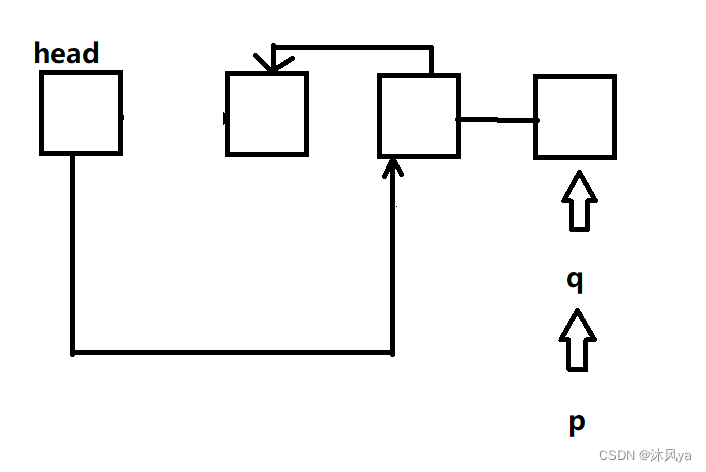
之后head指向p,p指向q

就变成这样啦~ 

因为此时p不为空,因此继续循环

 q指向p的下一个结点,因为在上一步时,p指向q,所以p也指向q指向的地方

之后,p指向head->next

 然后,head重新指向p(但记得我们最终要将结点连接起来,p和q只是用来当工具的哈)

循环内的最后又是将p移动啦

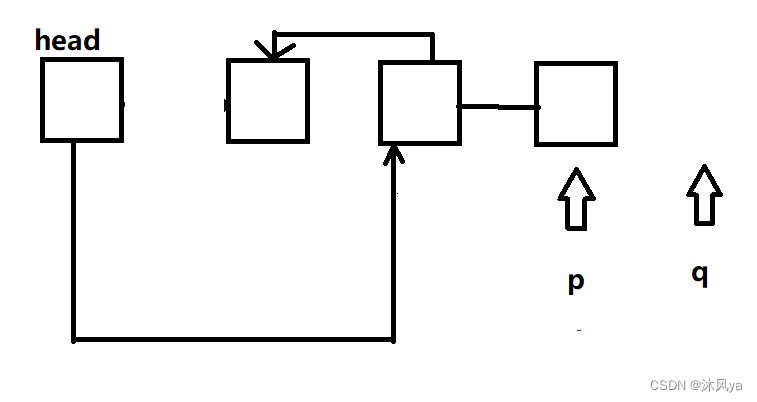
p此时还不是空呢,因此继续循环,但我们现在可以先停下来观察,我们发现此时head后连接的是我们原来的第二个结点,接下来是第一个结点,我们的逆置操作已经实现2/3啦! 

 还是像上面那样稍微处理一下q的移动,此时q已经是空啦

 然后,p指向head->next,相当于将原来这两个结点的指向关系相反过来(原本是第二个结点是指向第三个结点的)

 继续将head的指向关系更新(感觉逆置的核心就是这个捏)

 此时我们就已经能发现,已经完成逆置啦,我们可以通过头结点先访问原本的第三个数据啦

最后就是p指向q,而q为NULL,所以p为空,不符合循环条件,从而跳出函数

9.合并链表

//合并链表
void merge(node* h1, node* h2) {
	h1 = found(h1);
	h2 = found(h2);
	node * h3, * p, * q, * t;
	p = h1->next, q = h2->next;
	h3 = t = h1;
	while (p != NULL && q != NULL) {
		if (p->data <= q->data) {
			t->next = p;
			t = p;
			p = p->next;  
		}
		else {
			t->next = q;
			t = q;
			q = q->next;
		}
	}
	if (p != NULL) {
		t -> next = p;
	}
	if (q != NULL) {
		t->next = q;
	}
	free(h2);
	display(h3);
}

这里我写的是按照数据大小以升序合并在一条新链表中(但是只适用于两条原链表本就是升序)

这里我是将每个模块分装成函数后,创建了两条链表h1,h2

p和q分别指向他们除头结点后的第一个结点,

这里,新链表的表头我们使用h1的头结点,并且设置一个新的头结点h3来接收,并且定义一个工具人t来完成操作

合并的时候,我们需要分别遍历完h1和h2,而遍历完成的条件就是p和q均指向空

循环体就是比较此时p和q指向的结点数据,如果p的数据小,则新链表的头结点t来指向p,完成后t移动到p的位置,并且p也移到原链表h1的下一个结点

这样不断重复该操作,就可以率先完成链表长度较短的那一条,剩下那个没有完成的直接拼接在t后面即可

 因为我们之前是以h1的头结点作为新链表的头结点,因此可以通过打印h1或者h3来打印新链表,而h2此时已经没有用了,直接释放掉即可

单向链表里我知道的内容应该就这么多了,希望这篇文章可以帮到你~

感谢观看=)