Leetcode刷题笔记:链表篇
1.Leetcode203 移除链表元素(题解)
难度:⭐️
题意:删除链表中等于给定值 val 的所有节点。
这里以链表 1 4 2 4 来举例,移除元素4。
![]()
如果使用C,C++编程语言的话,不要忘了还要从内存中删除这两个移除的节点, 清理节点内存之后如图:
当然如果使用java ,python的话就不用手动管理内存了。
还要说明一下,就算使用C++来做leetcode,如果移除一个节点之后,没有手动在内存中删除这个节点,leetcode依然也是可以通过的,只不过,内存使用的空间大一些而已,但建议依然要养成手动清理内存的习惯。
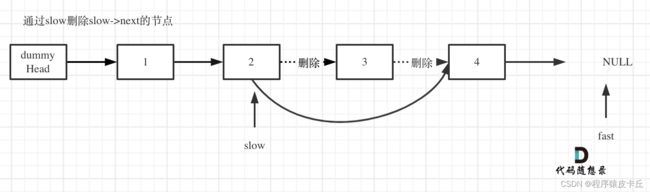
这种情况下的移除操作,就是让节点next指针直接指向下下一个节点就可以了,
那么因为单链表的特殊性,只能指向下一个节点,刚刚删除的是链表的中第二个,和第四个节点,那么如果删除的是头结点又该怎么办呢?
这里就涉及如下链表操作的两种方式:
- 直接使用原来的链表来进行删除操作。
- 设置一个虚拟头结点在进行删除操作。
来看第一种操作:直接使用原来的链表来进行移除。
![]()
移除头结点和移除其他节点的操作是不一样的,因为链表的其他节点都是通过前一个节点来移除当前节点,而头结点没有前一个节点。
所以头结点如何移除呢,其实只要将头结点向后移动一位就可以,这样就从链表中移除了一个头结点。
![]()
依然别忘将原头结点从内存中删掉。![]()
这样移除了一个头结点,是不是发现,在单链表中移除头结点 和 移除其他节点的操作方式是不一样,其实在写代码的时候也会发现,需要单独写一段逻辑来处理移除头结点的情况。
那么可不可以 以一种统一的逻辑来移除 链表的节点呢。
其实可以设置一个虚拟头结点,这样原链表的所有节点就都可以按照统一的方式进行移除了。
来看看如何设置一个虚拟头。依然还是在这个链表中,移除元素1。
![]()
这里来给链表添加一个虚拟头结点为新的头结点,此时要移除这个旧头结点元素1。
这样是不是就可以使用和移除链表其他节点的方式统一了呢?
来看一下,如何移除元素1 呢,还是熟悉的方式,然后从内存中删除元素1。
最后呢在题目中,return 头结点的时候,别忘了 return dummyNode->next;, 这才是新的头结点(不直接return head,因为可能已经被删了)
两个小tips:
1. 一开始让cur==head/dummy head而不是next的原因是,当删除节点时,需要将被删除节点的前一个节点的next,指向被删除节点的下一个节点。如果用cur直接指向被删除节点,由于是单链表,无法找到上一个节点的位置。因此一开始让cur指向被删除节点的前一个节点,并通过cur->next=cur->next->next来删除该节点。
2.使用C++时,删除链表元素后,需要手动进行内存释放delete
含注释的题解代码:无虚拟头节点、虚拟头节点。
另外我发现本题Leetcode控制台的输入输出是一个初始化列表(字符串),如[1,2,3,4],而Solution函数传入的参数和返回值却是链表的头指针。
看了Leetcode后台代码后才发现,原来在main函数那里对输入输出的格式进行了转换(先以string对象读取[1,2,3.4],切割掉两端空格和[],然后将”1,2,3,4”传入stringstream流对象,然后用getline以分隔符,读取,将每个元素用stoi转化为int后,压入vector
2.Leetcode707设计链表(题解)
难度:⭐️⭐️⭐️
这道题目设计链表的五个接口:
- 获取链表第index个节点的数值
- 在链表的最前面插入一个节点
- 在链表的最后面插入一个节点
- 在链表第index个节点前面插入一个节点
- 删除链表的第index个节点
可以说这五个接口,已经覆盖了链表的常见操作,是练习链表操作非常好的一道题目
小Tips:
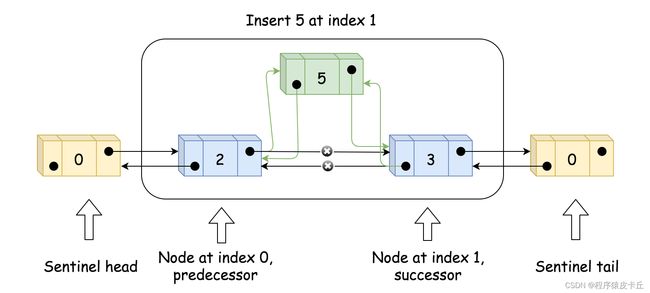
1. 增加/删除操作时,让cur->next(而非cur)指向待处理节点,因为我们需要对待处理节点的前一个节点的成员变量next进行处理。如果直接让cur指向待处理节点,在单链表中无法直接找到前一个节点。
![]()
2.增加节点时,记得先将新节点的next指向cur->next,然后再让cur->next指向新节点,注意顺序不要反。
3.题目中给出的类MyLinkedList,用于控制整个链表,因此应包含size和dummyNode两个成员变量,构造函数及若干成员函数。我们还需要再定义一个类(结构体)LinkedNode,用于存放链表中的每个节点。
题解代码中将LinkedNode定义在了类内部,称为嵌套类,可将类LinkedNode看作MyLinkedList的友元类。相比友元类不同的是,LinkedNode无需作用域运算符,即可直接访问MyLinkedList的public、protected、private成员。此外,如果嵌套类被定义在private/protected,将影响派生类/类外部对其访问(public则无影响)。当然,也可以直接把LinkedNode定义在类外(非嵌套类)。
另外本题也可以用双链表来做,具体实现代码。
双向链表相比单链表,主要有以下几点不同:
- 初始化MyLinkedList时,需要建立两个虚拟节点dummyhead, dummytail,并且需要让dummyhead->next=dummytail,dummytail->prev=dummyhead,不要忘记了。
- 查找索引所在元素时,需要比较从左向右(index<=(0+(size-1))/2),还是从右向左遍历快。
- 从右向左遍历时,需要取镜像索引index=size-1-index,作为while循环的条件。
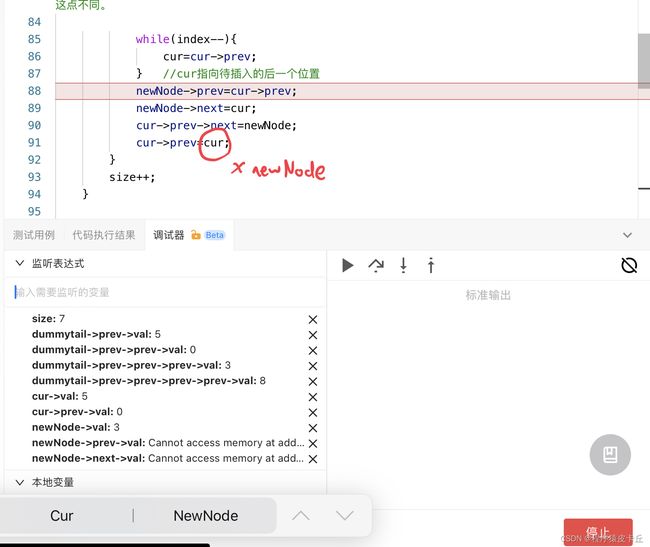
- (易错)从左向右遍历时,遍历到插入位置的前一个位置(index-1),从右往左遍历时,遍历到插入位置的后一个位置(index),当使用镜像索引时,while(size-1-index)结束后,只会遍历到index的后一个位置(index+1),所以还需要再往前遍历一个节点,到index所在位置。所以while循环成立的条件时size-index而不是size-index-1!
- 插入节点时,需要改四个成员变量;删除节点时,需要改两个成员变量,以及一次delete操作。
这题我用单链表做完,本来只想给两星难度的,没想到双链表的实现折腾了好几个小时,里面有不少细节问题。debug也很麻烦,需要把各个节点的值打出来,然后反复和结果值对比定位错误点。我最后有一个小bug找了快两个小时才找到T T……
出于对双链表的尊敬,本题难度额外再加一星QWQ。
3.Leetcode206反转链表(题解)
难度:⭐️
这道题难度不是太高,很容易想到暴力解法,空间复杂度为O(n),题解给出了迭代和递归两种解法。核心思想是双指针。
暴力解法定义一个新的链表(数组,向量),实现链表元素的反转,其实这是对内存空间的浪费。
其实只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表,如图所示:
![]()
之前链表的头节点是元素1, 反转之后头结点就是元素5 ,这里并没有添加或者删除节点,仅仅是改变next指针的方向。这种方法的空间复杂度降低为O(1)。
那么接下来看一看是如何反转的呢?
我们可以用迭代的方式来实现。拿有示例中的链表来举例,如动画所示:(纠正:动画应该是先移动pre,在移动cur)
首先定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。
然后就要开始反转了,首先要把 cur->next 节点用tmp指针保存一下,也就是保存一下这个节点。
为什么要保存一下这个节点呢,因为接下来要改变 cur->next 的指向了,将cur->next 指向pre ,此时已经反转了第一个节点了。
接下来,就是循环走如下代码逻辑了,继续移动pre和cur指针。
最后,cur 指针已经指向了null,循环结束,链表也反转完毕了。 此时我们return pre指针就可以了,pre指针就指向了新的头结点。
具体实现代码。
另外还有一种方法是递归,核心还是双指针的思想,又分为两种细分的写法:迭代前完成反转,迭代后完成反转。题解还给了一种巧妙的写法,只需用一个递归函数和一个节点指针head就可以完成递归。不过相比迭代的O(1),递归的空间复杂度为O(n),因为递归过程调用的栈空间最多为n层。
4.Leetcode 24 两两交换链表中的节点(题解)
难度:⭐️⭐️⭐️
自己摸索出来的解法,基本是按照从前往后的顺序依次迭代。
首先定义两个指针pre和cur。每当cur指向偶数位,且不空时,进入循环体(此时pre指向cur的前两个节点的位置)。如[1,2,3,4,5,6]第二次循环开始时,pre指向2,cur指向4(只有第一次循环比较特别,pre指向cur前面一个节点,即pre指向1,cur指向2)
循环体内做三件事(分别修改pre,pre->next,cur的next值):
- 修改cur前两个节点pre的next值:让tmp2=pre->next; pre.next->cur,然后pre移动到cur前一个节点位置pre=tmp2;(第一次循环无此步骤)
- 交换cur和cur前一个节点(pre): tmp=cur->next; pre.next=cur->next; cur->next=pre;之后让cur指向下一个奇数节点的位置
- 判断下一个奇数节点是否存在,如果空,表明链表一共有偶数个节点,直接返回结果。如果不空,则让cur继续往前指向下一个偶数节点,然后进入下一次循环条件判定(注意此时pre指向的是上个偶数节点的位置)
- 如果新的偶数节点为空,那说明链表一共有奇数个节点,最后一个单独的节点无需修改。如果不空,则说明接下来至少还有两个成对的节点,于是再次进入循环体,完成三个节点next值的修改。
具体实现代码。
代码写完后,我又捋了一遍思路,这道题的核心就在循环体内三个节点next值的替换。我觉得有以下两点可以继续完善。
- 可以加入一个虚拟头节点dummyhead,然后一开始让pre指向dummyhead,这样第一次循环也可以完整兼容循环体内的全部内容。
- 循环一开始时,可以先让cur指向奇数节点(用cur->next判断是否为空),这样不用再建立一个临时节点tmp2来存储cur的位置。只需让pre->next=cur->next; pre=cur; cur=cur->next; 即可
改进后的代码。
最后看了一下题解代码,发现我还是太naive了,只需要一个cur就可以完成遍历,而且奇数节点和偶数节点的判断条件也可以一起放到循环条件中,最后返回值直接是dummy->next就行了,无需对head额外判断。
这道题目正常模拟就可以了。
建议使用虚拟头结点,这样会方便很多,要不然每次针对头结点(没有前一个指针指向头结点),还要单独处理。
接下来就是交换相邻两个元素了,此时一定要画图,不画图,操作多个指针很容易乱,而且要操作的先后顺序
初始时,cur指向虚拟头结点,然后进行如下三步:
(我自己实现题解代码时,用的步骤一,步骤三,步骤二的顺序,也没问题)
本题时间复杂度O(n),空间复杂度O(1)。
5. Leetcode 19删除链表中倒数第N个节点(题解)
难度:⭐️⭐️
这道题我首先想到的是暴力解法,先遍历一遍链表,得到总长度count,然后再计算出待删除节点的正向索引index=count-n。那么只需要再遍历一次,遍历到待删除节点的前一个节点的位置,然后进行节点删除操作即可。这种方法需要遍历链表两次,时间复杂度为O(2n)。
进阶解法是只遍历一次链表,那么时间复杂度降低到O(n)。
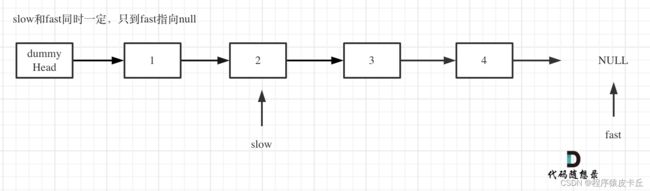
本题为双指针的经典应用,如果要删除倒数第n个节点,首先让fast移动n步,然后让fast和slow同时移动,直到fast指向链表末尾。删掉slow所指向的节点就可以了。
思路是这样的,但要注意一些细节。
分为如下几步:
-
首先这里我推荐大家使用虚拟头结点,这样方便处理被删除节点为链表首节点的情况。
-
定义fast指针和slow指针,初始值为虚拟头结点,如图:
-
fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
-
fast和slow同时移动,直到fast指向末尾,如图:
-
当然,以上只是双指针解法的大体思路,具体实现细节不唯一。我自己写的代码中,让fast先比slow往前走n步(并加入了n范围的判断,如果在这n步中fast->next==nullptr,那么待删除节点不在链表中,直接返回原链表)然后当fast走到链表末尾节点(fast->next==nullptr)时,结束循环。此时由于fast比slow快n步,所以slow指向的是从右往左第n+1个节点,也就是待删除节点的前一个节点。接下来执行删除节点的操作即可。
-
(个人觉得我的解法细节,比原题解的要好一点,用fast->next判断终止条件,只需前进n步即可)
6. Leetcode 160链表相交(题解)
难度:⭐️⭐️
这道题看懂题目就花了一些时间,题目描述中给了五个参数,但Solution里只有两个。其实这五个参数是为了辅助Leetcode后台判题程序,将原本的输入内容(字符串listA, listB)转化成链表形式(头节点指针headA, headB),然后传到我们写的Solution成员函数中调用并返回结果,最后比较是否和标准答案一致。具体实现可参考playground代码(参考本文第一题的playground部分)。
然而问题是,编辑器给的playground代码还是和第一题一样,这显然不符合本题的意图。因此应该Leetcode后台是用另外的代码实现的。我的理解是,首先还是按照原代码的方法,先切割listA字符串,生成vector再转化成链表A,返回头指针head。区别在链表B的生成,这时候就要用到skipA和skipB参数了,首先B的前skipB个节点,还是按之前的方式生成,然后接下来的每个节点就不用new了,直接将B的当前节点遍历指针cur->next指向A中对应相交首节点的地址(可以通过遍历A的前skipA个节点找到,下一个节点便是),然后一直循环遍历并赋值cur->next,直到A的最后一个节点(这也是B的最后一个节点)为止。这样就保证了A,B相交节点的地址相同,也解释了为什么例1中相交首节点是8而不是1,因为实际构造链表时,是从8才开始相交的(多亏有你们呀skipA/B)。
至于playground写的输出格式,还是和第一题的输出一样,显然不符合本题的意图。应该只需要比较一下intersecVal是否和我们Solution返回的相交首节点指针的val相同即可。
接下来开始分析题目。这道题比较节点值相等来判断相交条件的方式显然是行不通的,正如例1所示。核心突破口,便是在节点的地址。只要A和B中某个节点的地址相等,就说明这个节点便是A和B的相交首节点。然后返回具体的值即可。
那么如何找到相同地址的节点呢?
首先想到的是暴力解法,设置两个指针cur1=headA, cur2=headB,然后两层while循环,分别遍历A和B的所有节点,找到地址相同的节点cur1=cur2并返回。时间复杂度为O(mn)。
如何改进算法,让时间复杂度降低到O(m+n)呢?
这里就要用到链表中节点的定义了,可以让两个节点的next指向同一个相交节点,但不能让一个节点的next同时指向两个不同的节点。也就是说,两个链表一旦相交,从相交节点开始,之后的每个节点,必然完全相同,直到链表结束(nullptr)为止。
明白这点之后,我们只需要将两个链表右对齐,然后从短的那个链表的头节点位置开始同时遍历两个链表,直到找到首个地址相同(而非值相等)的节点,即为相交首节点。
(注意图片中的错误,链表B中最后一个节点应为2)
具体实现代码。
7.Leetcode 142环形链表II(题解)
难度:⭐️⭐️⭐️⭐️
这道题我本来自己做完后,只想给两颗星难度的,结果看了题解后,果断再加两颗星!!
一开始的思路是,环形不就是重复了嘛?那只需要从头开始遍历,找到第一个重复的节点,那便说明有环,同时这个节点就是环的入口。于是我用一个哈希表保存每个节点的地址,每次遍历时,判断一下是否新节点的地址已在哈希表中,如果找到那就返回这个节点,如果遍历完还没找到,就返回空指针,不就可以了嘛?就这?
具体实现代码。这个方法的时间复杂度为O(n),空间复杂度为O(n)。
然后题目扩展要求是,要O(1)的空间复杂度实现,这可难倒我了。看样子是得双指针了,可到底怎么才能实现呢?
这道题目,不仅考察对链表的操作,而且还需要一些数学运算。
主要考察两知识点:
- 判断链表是否环
- 如果有环,如何找到这个环的入口
#判断链表是否有环
可以使用快慢指针法,分别定义 fast 和 slow 指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环。
为什么fast 走两个节点,slow走一个节点,有环的话,一定会在环内相遇呢,而不是永远的错开呢
首先第一点:fast指针一定先进入环中,如果fast指针和slow指针相遇的话,一定是在环中相遇,这是毋庸置疑的。
那么来看一下,为什么fast指针和slow指针一定会相遇呢?
可以画一个环,然后让 fast指针在任意一个节点开始追赶slow指针。
会发现最终都是这种情况, 如下图:
![]()
fast和slow各自再走一步, fast和slow就相遇了
这是因为fast是走两步,slow是走一步,其实相对于slow来说,fast是一个节点一个节点的靠近slow的,所以fast一定可以和slow重合。
动画如下:
#如果有环,如何找到这个环的入口
此时已经可以判断链表是否有环了,那么接下来要找这个环的入口了。
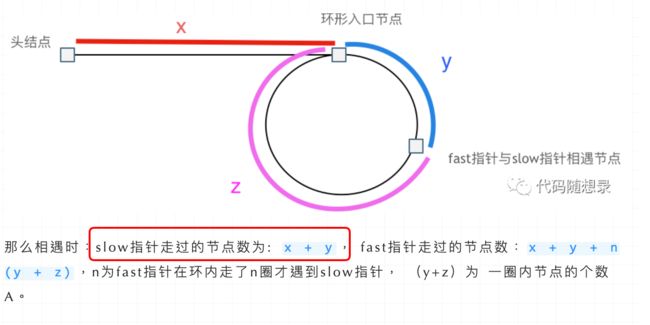
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示:
![]()
那么相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈内节点的个数A。
因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2:
(x + y) * 2 = x + y + n (y + z)
两边消掉一个(x+y): x + y = n (y + z)
因为要找环形的入口,那么要求的是x,因为x表示 头结点到 环形入口节点的的距离。
所以要求x ,将x单独放在左面:x = n (y + z) - y ,
再从n(y+z)中提出一个 (y+z)来,整理公式之后为如下公式:x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的,因为 fast指针至少要多走一圈才能相遇slow指针。
这个公式说明什么呢?
先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了。
当 n为1的时候,公式就化解为 x = z,
这就意味着,从头结点出发一个指针,从相遇节点 也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是 环形入口的节点。
也就是在相遇节点处,定义一个指针index1,在头结点处定一个指针index2。
让index1和index2同时移动,每次移动一个节点, 那么他们相遇的地方就是 环形入口的节点。
动画如下:
那么 n如果大于1是什么情况呢,就是fast指针在环形转n圈之后才遇到 slow指针。
其实这种情况和n为1的时候 效果是一样的,一样可以通过这个方法找到 环形的入口节点,只不过,index1 指针在环里 多转了(n-1)圈,然后再遇到index2,相遇点依然是环形的入口节点。
补充
在推理过程中,大家可能有一个疑问就是:为什么第一次在环中相遇,slow的 步数 是 x+y 而不是 x + 若干环的长度 + y 呢?
即文章中如下的地方:
首先slow进环的时候,fast一定是先进环来了。
如果slow进环入口,fast也在环入口,那么把这个环展开成直线,就是如下图的样子:
![]()
可以看出如果slow 和 fast同时在环入口开始走,一定会在环入口3相遇,slow走了一圈,fast走了两圈。
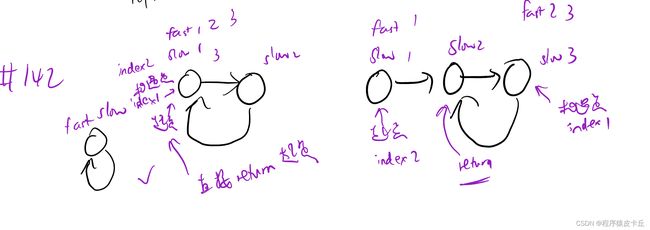
重点来了,slow进环的时候,fast一定是在环的任意一个位置,如图:
那么fast指针走到环入口3的时候,已经走了k + n 个节点,slow相应的应该走了(k + n) / 2 个节点。
因为k是小于n的(图中可以看出),所以(k + n) / 2 一定小于n。
也就是说slow一定没有走到环入口3,而fast已经到环入口3了。
这说明什么呢?
在slow开始走的那一环已经和fast相遇了。
那有同学又说了,为什么fast不能跳过去呢? 在刚刚已经说过一次了,fast相对于slow是一次移动一个节点,所以不可能跳过去。
好了,这次把为什么第一次在环中相遇,slow的 步数 是 x+y 而不是 x + 若干环的长度 + y ,用数学推理了一下,算是对这道题目的补充。
对于刚开始节点数比较少的特殊情况,我也试着用题解的方法模拟了一下,也是完美解决。
具体实现代码。
双指针解法的时间复杂度为O(n),因为第一个阶段slow指针到相遇点,第二个阶段index2指针到入口点的长度都小于链表长度,所以按照单位步长来走,总时间为O(n)。
总结:
文中部分内容参考自:代码随想录