动态规划：完全背包问题

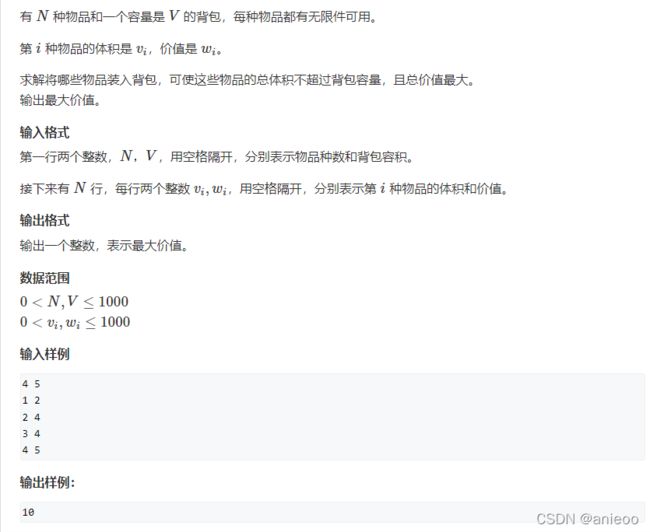
ACwing #3. 完全背包问题

完全背包问题和01背包问题很相似。
01背包问题每个物品只能选一个，而完全背包问题每个物品可以选无限次。

DP问题的关键是找到状态转移方程：

①定义f[i][j]表示从前 i 个物品中选择,体积为 j 的时候的最大价值。
②那么转移方程f[i][j] = max(f[i - 1][j],f[i - 1][j - v[i]],f[i - 1][j - 2 * v[i]],.....,f[i - 1][j - k * v[i]],....)

因此代码就是：

#include
using namespace std;
const int N = 1010;
int f[N][N];
int v[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++)
    {
        scanf("%d%d",&v[i],&w[i]);
    }

    for(int i = 1 ; i<=n ;i++)
    for(int j = 1 ; j<=m ;j++)
    {
        for(int k = 0 ; k*v[i]<=j ; k++)
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
    }

    printf("%d",f[n][m]
    return 0;
}

由于数据量级的原因，此代码肯定会发生TLE，因此需要进行优化。

f[i , j ] = max( f[i-1,j] , f[i- 1,j - v[i]+ w[i] ,  f[i - 1,j-2 * v[i]]+2 * w[i] , f[i -1,j - 3 * v[i]]+3 * w[i] , .....)
f[i , j - v[i]]= max(       f[i - 1,j - v[i]] ,         f[i - 1,j - 2 * v[i]] + w[i] , f[i - 1,j- 3 * v[i]]+2 * w[i] , .....)

由上两式，可得出如下递推关系： 
                        f[i][j]=max(f[i, j - v[i] ] + w[i] , f[i - 1][j])  

因此优化后的代码变为：

#include 
using namespace std;
const int N=1010;
int v[N],w[N],f[N][N];
int n,m;

int main()
{
  scanf("%d%d",&n,&m);
  
  for(int i = 1;i <= n;i++){
      scanf("%d%d",&v[i],&w[i]);
  } 
  for(int i = 1;i <= n;i++)
    for(int j = 1;j <= m;j++){
      f[i][j] = f[i - 1][j];
      if(j >= v[i])
        f[i][j] = max(f[i][j],f[i][j - v[i]] + w[i]);
    }
    
  printf("%d",f[n][m]);
  return 0;
}

        可以看出代码与01背包非常相似,因此尝试能否做进一步优化。

优化完成后的状态转移方程：f[j] = max(f[j], f[j - v[i]] + w[i]) 

代码如下：

#include 
using namespace std;

const int N=1010;
int v[N],w[N],f[N];
int n,m;

int main()
{
  scanf("%d%d",&n,&m);  
  for(int i = 1;i <= n;i++){
      scanf("%d%d",&v[i],&w[i]);
  } 
  for(int i=1;i<=n;i++)
    for(int j=v[i];j<=m;j++){
        f[j]=max(f[j],f[j-v[i]]+w[i]);
    }    
  printf("%d",f[m]);  
  return 0;
}