机器学习实战：Python基于KDE核密度估计进行分布估计（十六）

1. 前言

1.1 KDE简介

核密度估计（Kernel Density Estimation，简称KDE）是用于估计连续随机变量概率密度函数的非参数方法。它的工作原理是在每个数据点周围放置一个“核”（通常是某种平滑的、对称的函数），然后将这些核加起来，形成一个整体的估计。这可以被视为对直方图的平滑，使得得到的密度函数更连续、更平滑。

KDE的主要组件是核函数和带宽。核函数确定了每个数据点对估计的贡献的形状，而带宽决定了核的宽度，影响估计的平滑程度。正确选择这两个组件对于获得有意义的估计至关重要。

优点：

• 非参数性：KDE不假设数据遵循任何特定的概率分布，使其具有很高的灵活性，能够适应多种不同的数据形态。

• 平滑性：与传统的直方图相比，KDE提供的概率密度估计是平滑的，它可以揭示数据中的细微特征而不是粗糙的组块。

• 数据探索：KDE对于初步的数据探索和可视化非常有用，可以帮助我们直观地了解数据的分布和形状。

• 核的选择：KDE允许使用不同的核，例如高斯核、三角核等，这为不同的应用和数据特点提供了选择的灵活性。

缺点：

• 计算复杂性：KDE的计算复杂性可以高，特别是当数据集很大时，因为它需要考虑每个数据点与其他所有数据点的关系。

• 带宽选择：带宽是KDE中最关键的参数。不合适的带宽选择可能导致估计过于嘈杂（过小的带宽）或过于平滑（过大的带宽）。尽管有带宽选择的方法，但它们通常需要额外的计算和调优。

• 边界问题：在数据分布的边界附近，KDE可能不会提供良好的估计。这是因为在边界附近，核函数可能会延伸到数据的实际范围之外，导致边界处的估计偏低。

• 高维数据：随着数据维度的增加，KDE面临“维度灾难”。在高维空间中，数据点之间的距离变得相对更远，这使得密度估计变得更加困难。

1.2 KDE应用领域

核密度估计（KDE）是一种广泛应用的统计方法，它在多个领域都有其应用。以下是一些KDE部分应用领域的具体实例：

1. 数据探索和可视化：
   考虑一个电商网站，其中的产品有各种价格。为了了解大多数产品的价格范围，数据分析师可以使用KDE来估计价格分布。这不仅能够揭示价格的中心趋势，还可以揭示价格的多模态分布（例如，低端、中端和高端产品可能有明显的价格聚类）。
2. 异常检测：
   在信用卡欺诈检测中，可以使用KDE来估计正常的交易行为分布，例如交易金额和交易时间。然后，任何明显偏离这个估计的交易都可能被标记为可疑，然后进一步进行调查。
3. 地理空间分析：
   在城市治安管理中，警察部门可以利用KDE来分析报告的犯罪事件的地理位置，以确定犯罪的“热点”地区。这可以帮助他们更有效地部署警力和资源。
4. 图像处理：
   在医学图像分析中，KDE可以用于估计某一区域（如肿瘤）的像素强度分布。这有助于区分正常组织和异常组织，并可以用于自动检测和标记潜在的问题区域。
5. 生物信息学：
   考虑一项研究，旨在分析不同类型的细胞在特定环境下的基因表达。KDE可以用于估计特定基因在各种条件下的表达水平分布，从而帮助研究人员了解基因的激活和抑制模式。
6. 市场研究：
   一个汽车制造商想要了解其竞争对手车型的价格分布。使用KDE，他们可以揭示市场上的价格段，并据此确定他们自己车型的定价策略。

2. diy数据集实战演示

2.1 导入函数

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
from sklearn.model_selection import GridSearchCV

2.2 自定义数据

生成一个数据集，其中数据来自两个不同的分布：一个对数正态分布和一个正态分布。两个分布各生成1000个数据点，并将这些数据点连接在一起：

• 对数正态分布使用均值0和标准差0.3。
• 正态分布使用均值3和标准差1。

def generate_data(rand=None):
    if rand is None:
        rand = np.random.RandomState()
    
    dat1 = rand.lognormal(0, 0.3, 1000)
    dat2 = rand.normal(3, 1, 1000)
    x = np.concatenate((dat1, dat2))
    return x

data = generate_data(np.random.RandomState(17))
data[:10]

# array([1.08641118, 0.57327576, 1.20583266, 1.41000519, 1.3650037 ,
#       1.76119346, 0.96704574, 0.89706191, 1.04561216, 0.876924  ])

2.3 可视化数据

• 展示数据点的顺序和相对位置
• 展示数据的分布情况

x_train = generate_data()[:, np.newaxis]
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))

ax[0].scatter(np.arange(len(x_train)), x_train, c='red')
ax[0].set_xlabel('Sample no.')
ax[0].set_ylabel('Value')
ax[0].set_title('Scatter plot')

ax[1].hist(x_train, bins=50)
ax[1].set_title('Histogram')

fig.subplots_adjust(wspace=.3)
plt.show()

2.4 KDE建模

x_test = np.linspace(-1, 7, 2000)[:, np.newaxis]
model = KernelDensity().fit(x_train)
log_dens = model.score_samples(x_test)

plt.fill_between(x_test.ravel(), np.exp(log_dens), color='pink')
plt.show()

3. 参数探讨

3.1 带宽

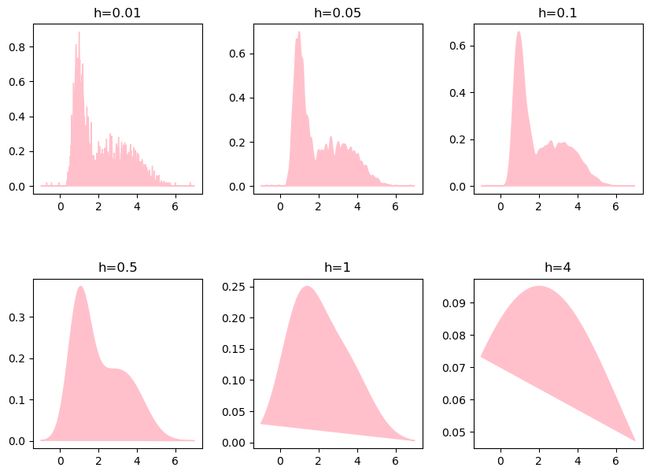
带宽（bandwidth）是核密度估计（KDE）中的一个关键参数，它决定了估计的平滑程度。选择合适的带宽对于获得有意义的密度估计至关重要。

bandwidths = [0.01, 0.05, 0.1, 0.5, 1, 4]
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(10, 7))

for ax, b in zip(axes.ravel(), bandwidths):
    kde_model = KernelDensity(kernel='gaussian', bandwidth=b).fit(x_train)
    score = kde_model.score_samples(x_test)
    ax.fill(x_test, np.exp(score), c='pink')
    ax.set_title(f"h={b}")

fig.subplots_adjust(hspace=0.5, wspace=.3)
plt.show()

3.2 选择最佳带宽

常见的就这四种方法：

1. 经验法则：一些常见的方法，如Silverman’s rule，可以为一般情况提供一个好的起点。但这些方法可能不适用于所有数据集。

2. 交叉验证：使用交叉验证选择带宽是一种常见方法。这涉及到将数据分成训练集和验证集，然后对于不同的带宽值，使用训练集进行拟合，并使用验证集计算对数似然评分。选择使得评分最大化的带宽值。

3. 可视化：像您之前的代码那样，通过为不同的带宽值绘制KDE，可以帮助直观地选择一个合适的带宽。

4. 数据的范围和分辨率：带宽的绝对值通常与数据的范围和单位有关。例如，如果数据是以米为单位的距离测量值，那么0.01米的带宽与100米的带宽意味着完全不同的事情。

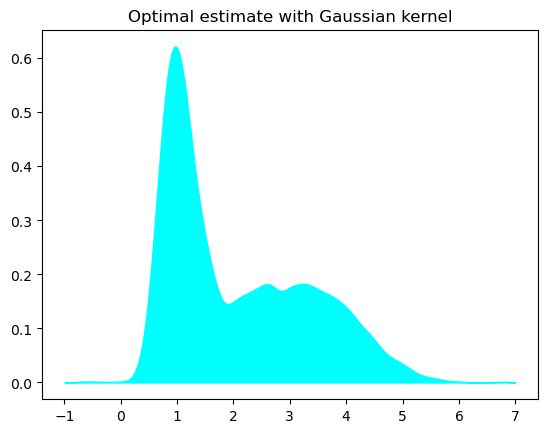
这里用的是交叉验证：

bandwidth = np.arange(0.05, 2, .05)
grid = GridSearchCV(KernelDensity(kernel='gaussian'), {'bandwidth': bandwidth})
grid.fit(x_train)

kde = grid.best_estimator_
log_dens = kde.score_samples(x_test)

plt.fill_between(x_test.ravel(), np.exp(log_dens), color='cyan')
plt.title('Optimal estimate with Gaussian kernel')
plt.show()
print(f"optimal bandwidth: {kde.bandwidth:.2f}")

# optimal bandwidth: 0.15

3.2 核函数

Kernel	Name	Description
cosine	余弦	形状类似于余弦曲线的一部分，平滑地从中心下降到零。
epanechnikov	Epanechnikov	这是一个凸的、平滑的、有界的核，常被用作默认核，因为它在某些理论性质上优于其他核。
exponential	指数	这是一个从中心点开始快速下降的核，类似于高斯核，但下降得更快。
gaussian	高斯或正态	这是最常用的核，其形状是标准的正态分布曲线。它为数据点提供了平滑的、无界的权重。
linear	线性	这是一个三角形的核，从中心线性下降到零。
tophat	平顶帽	这是一个矩形的核，它在一个固定的范围内为数据点提供均匀的权重，然后突然下降到零。

吐槽一点，“Epanechnikov” 核函数并没有一个广泛接受的中文名字。它是以俄罗斯统计学家Urii Epanechnikov的名字命名的。文献常见被翻译成 “埃潘尼克尼科夫” 核。

kernels = ['cosine', 'epanechnikov', 'exponential', 'gaussian', 'linear', 'tophat']
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(10, 7))
x_range = np.arange(-2, 2, 0.1)[:, None]

for ax, k in zip(axes.ravel(), kernels):
    kde_model = KernelDensity(kernel=k).fit([[0]])
    score = kde_model.score_samples(x_range)
    ax.fill(x_range, np.exp(score), c='blue')
    ax.set_title(k)

fig.subplots_adjust(hspace=0.5, wspace=.3)
plt.show()

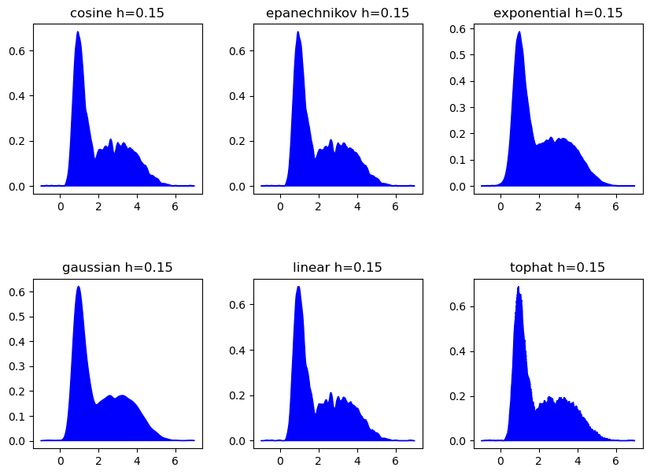
3.4 挑选合适核函数

这里直接用刚刚的最佳带宽0.15即可

def my_scores(estimator, X):
    scores = estimator.score_samples(X)
    scores = scores[scores != float('-inf')]
    return np.mean(scores)

kernels = ['cosine', 'epanechnikov', 'exponential', 'gaussian', 'linear', 'tophat']
h_vals = np.arange(0.05, 1, .1)
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(10, 7))

for ax, k in zip(axes.ravel(), kernels):
    grid = GridSearchCV(KernelDensity(kernel=k), {'bandwidth': h_vals}, scoring=my_scores)
    grid.fit(x_train)
    kde = grid.best_estimator_
    log_dens = kde.score_samples(x_test)
    ax.fill(x_test.ravel(), np.exp(log_dens), c='cyan')
    ax.set_title(f"{k} h={kde.bandwidth:.2f}")

fig.subplots_adjust(hspace=.5, wspace=.3)
plt.show()

还是用交叉验证：

grid = GridSearchCV(KernelDensity(),
                    {'bandwidth': h_vals, 'kernel': kernels},
                    scoring=my_scores)
grid.fit(x_train)

best_kde = grid.best_estimator_
log_dens = best_kde.score_samples(x_test)

plt.fill_between(x_test.ravel(), np.exp(log_dens), color='cyan')
plt.title(f"Best Kernel: {best_kde.kernel} h={best_kde.bandwidth:.2f}")
plt.show()

4. 讨论

核密度估计（KDE）是一种非参数方法，用于估计随机变量的概率密度函数。通过在每个观测数据点处放置一个核函数并将它们相加，KDE提供了数据的平滑估计，可以捕捉数据的复杂分布特性，而不受特定参数分布的限制。