【LeetCode】剑指 Offer Ⅱ 第5章:哈希表(6道题) -- Java Version
题库链接:https://leetcode.cn/problem-list/e8X3pBZi/
| 类型 | 题目 | 解决方案 |
|---|---|---|
| 哈希表的设计 | 剑指 Offer II 030. 插入、删除和随机访问都是O(1) 的容器 | HashMap + ArrayList ⭐ |
| 剑指 Offer II 031. LRU 缓存 | HashMap + 双向链表 ⭐ | |
| 哈希表的应用 | 剑指 Offer II 032. 有效的变位词 | 哈希表:数组模拟哈希表 ⭐ |
| 剑指 Offer II 033. 变位词组 | 排序:Arrays.sort(arr) ⭐ | |
| 剑指 Offer II 034. 外星语言是否排序 | 哈希表:数组模拟哈希表 ⭐ | |
| 剑指 Offer II 035. 最小时间差 | 排序:计算两两差值 + 鸽巢原理 ⭐ |
本章主要练习了基本的哈希表设计和应用:
- 哈希表的时间效率很高,添加、删除和查找操作的时间复杂度都是 O(1);
- 哈希表经常被用来记录字符串中字母出现的次数、字符串中字符出现的位置等信息;
- 如果哈希表的键的数目是固定的,并且数目不太大,那么也可以使用数组来模拟哈希表,数组的下标对应哈希表的键,而数组的值则与哈希表的值对应。(与哈希表相比,数组的代码更加简洁,应聘者在面试时只要情况允许就可以尽量使用数组模拟哈希表)
1. 剑指 Offer II 030. 插入、删除和随机访问都是O(1) 的容器 – P76
设计一个支持在平均 时间复杂度 O(1) 下,执行以下操作的数据结构:
- insert(val):当元素 val 不存在时返回 true ,并向集合中插入该项,否则返回 false 。
- remove(val):当元素 val 存在时返回 true ,并从集合中移除该项,否则返回 false 。
- getRandom:随机返回现有集合中的一项。每个元素应该有 相同的概率 被返回。
1.1 HashMap + ArrayList – O(1)(⭐)
时间复杂度 O ( 1 ) O(1) O(1),空间复杂度 O ( n ) O(n) O(n)
注意:该题比较麻烦的地方在于删除一个元素,本题解采用的方法是通过交换删除元素与变长列表中最后一个元素的位置,删除最后一个元素实现的,使用这种方法可以避免移动被删除元素后面的元素。
class RandomizedSet {
Map<Integer,Integer> map;
List<Integer> list;
Random random;
/** Initialize your data structure here. */
public RandomizedSet() {
map = new HashMap<>();
list = new ArrayList<>();
random = new Random();
}
/** Inserts a value to the set. Returns true if the set did not already contain the specified element. */
public boolean insert(int val) {
if (map.containsKey(val)) return false; // val存在 返回false
int index = map.size();
map.put(val,index);
list.add(val);
return true;
}
/** Removes a value from the set. Returns true if the set contained the specified element. */
public boolean remove(int val) {
if (!map.containsKey(val)) return false; // val不存在 返回false
int index = map.get(val); // val 在变长数组中的索引位置
int last = list.get(list.size()-1); // 变长数组中最后位置的元素
list.set(index, last); // 交换元素
map.put(last, index);
list.remove(list.size()-1); // 删除元素
map.remove(val);
return true;
}
/** Get a random element from the set. */
public int getRandom() {
int randomIndex = random.nextInt(list.size());
return list.get(randomIndex);
}
}
/**
* Your RandomizedSet object will be instantiated and called as such:
* RandomizedSet obj = new RandomizedSet();
* boolean param_1 = obj.insert(val);
* boolean param_2 = obj.remove(val);
* int param_3 = obj.getRandom();
*/
2. 剑指 Offer II 031. LRU 缓存 – P79
运用所掌握的数据结构,设计和实现一个 LRU (Least Recently Used,最近最少使用) 缓存机制 。
实现 LRUCache 类
- LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存;
- int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 ;
- void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
2.1 HashMap + 双向链表 – O(1)(⭐)
时间复杂度 O ( 1 ) O(1) O(1),空间复杂度 O ( n ) O(n) O(n)
提示:此处双向链表使用头插法或者尾插法均可,尾插法代码可参考:
- LCR 031. LRU 缓存 - 力扣(LeetCode)
class LRUCache {
// 1. 头插法,从头节点插入,从尾节点删除
class DuLNode { // 双向链表
DuLNode prev;
DuLNode next;
int key;
int value;
public DuLNode(){};
public DuLNode(int key, int value) {
this.key = key;
this.value = value;
}
}
DuLNode head; // 头节点
DuLNode tail; // 尾节点
int size; // 容量
Map<Integer,DuLNode> map;
public LRUCache(int capacity) {
size = capacity;
map = new HashMap<>();
head = new DuLNode();
tail = new DuLNode();
head.next = tail; // head 和 tail 是两个哨兵节点
tail.prev = head;
}
public void deleteNode(DuLNode node) { // 删除链表中的某节点
node.prev.next = node.next;
node.next.prev = node.prev;
}
public void addToHead(DuLNode node) { // 链表头插法
node.next = head.next;
head.next.prev = node;
head.next = node;
node.prev = head;
}
public void moveToHead(DuLNode node) { // 将某节点移动到头
deleteNode(node);
addToHead(node);
}
public int get(int key) {
if (!map.containsKey(key)) return -1;
DuLNode node = map.get(key);
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
if (map.containsKey(key)) {
DuLNode node = map.get(key);
node.value = value;
moveToHead(node);
} else {
DuLNode node = new DuLNode(key, value);
if (map.size() == size) {
DuLNode delete = tail.prev;
deleteNode(delete);
map.remove(delete.key);
}
map.put(key, node);
addToHead(node);
}
}
}
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache obj = new LRUCache(capacity);
* int param_1 = obj.get(key);
* obj.put(key,value);
*/
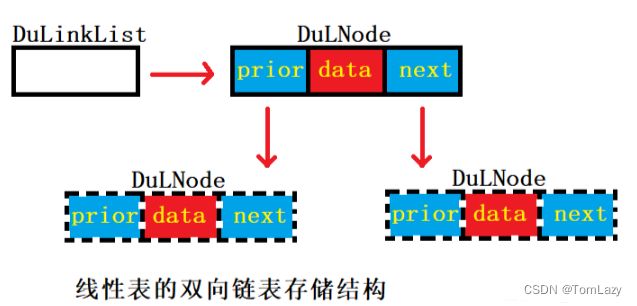
PS:补充知识1 - 【双向链表】
可参考:
[1] 数据结构笔记(六)-- 双向链表 - 淡定的炮仗的博客【图解鲜明】
[2] 线性表的链式表示-双向链表 - yunfan188的博客【代码示例】
// 线性表的双向链表存储结构
class DuLNode { // 双向链表
DuLNode prev;
DuLNode next;
int key;
int value;
public DuLNode(){};
public DuLNode(int key, int value) {
this.key = key;
this.value = value;
}
}
3. 剑指 Offer II 032. 有效的变位词 – P83
给定两个字符串 s 和 t ,编写一个函数来判断它们是不是一组变位词(字母异位词)。
……
注意: s 和 t 中每个字符出现的次数都相同且字符顺序不完全相同,才能称 s 和 t 互为变位词。
3.1 哈希表:数组模拟哈希表 – O(n)(⭐)
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( 26 ) O(26) O(26)
class Solution {
public boolean isAnagram(String s, String t) {
if (s.length() != t.length() || s.equals(t)) return false; // 长度不一致/两者一样
int[] map = new int[26];
for (char c : s.toCharArray()) { // 遍历 s,存入map
map[c-'a']++;
}
for (char c : t.toCharArray()) { // 遍历 t,存入map,并判断是否有字符次数不同的情况
map[c-'a']--;
if (map[c-'a'] < 0) return false;
}
return true;
}
}
进阶: 如果输入字符串包含 unicode 字符怎么办?你能否调整你的解法来应对这种情况?将 int[26] 数组替换成无固定大小的 HashMap 即可,但与 HashMap 相比,使用数组会更快一些,因此只要情况允许就应该尽量使用数组模拟哈希表。
class Solution {
public boolean isAnagram(String s, String t) {
if (s.length() != t.length() || s.equals(t)) return false; // 长度不一致/两者一样
Map<Character, Integer> map = new HashMap<>();
for (char c : s.toCharArray()) { // 遍历 s,存入map
map.put(c, map.getOrDefault(c,0)+1);
}
for (char c : t.toCharArray()) { // 遍历 t,存入map,并判断是否有字符次数不同的情况
map.put(c, map.getOrDefault(c,0)-1);;
if (map.get(c) < 0) return false;
}
return true;
}
}
3.2 排序:Arrays.sort(arr) – O(nlogn)
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn),空间复杂度 O ( l o g n ) O(logn) O(logn)
class Solution {
public boolean isAnagram(String s, String t) {
if (s.length() != t.length() || s.equals(t)) {
return false;
}
char[] str1 = s.toCharArray();
char[] str2 = t.toCharArray();
Arrays.sort(str1);
Arrays.sort(str2);
return Arrays.equals(str1, str2);
}
}
4. 剑指 Offer II 033. 变位词组 – P85
给定一个字符串数组 strs ,将 变位词 组合在一起。 可以按任意顺序返回结果列表。
4.1 映射:字符 - 质数 – O(mn)
时间复杂度 O ( m n ) O(mn) O(mn),空间复杂度 O ( n ) O(n) O(n)
说明:该解法是将 26 个小写字母均映射为了一个质数,这样的话,如果是变位词,那么一定具有相同的值。但该解法存在一个潜在的问题:即由于把字符映射到数字用到了乘法,因此当单词非常长时,乘法就有可能溢出。
class Solution {
// 1. 字符映射
public List<List<String>> groupAnagrams(String[] strs) {
int[] hash = new int[]{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101};
Map<Long, List<String>> map = new HashMap<>();
for (String str : strs) {
char[] ch = str.toCharArray();
long key = 1;
for (char c : ch) {
key *= hash[c-'a'];
}
map.putIfAbsent(key, new ArrayList<String>()); // key不存在,才加入
map.get(key).add(str);
}
return new ArrayList<>(map.values());
}
}
PS:补充知识1 - 【求质数】
可参考:
[1] Java求质数常见的3种方式 - 十三度灰的博客
以埃氏筛法(埃拉托斯特尼筛法)为例:【模板题】AcWing 868. 筛质数
原理:先把从2开始的所有数写下来,然后从2开始,将每个质数的倍数都标记成合数,即非质数,直到筛完所有小于等于给定数n的数。这样,留下的就是小于等于n的质数。
import java.util.*;
class Main {
// 1. 埃氏筛法
private final static int N = 1000010;
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
List<Integer> primes = new ArrayList<>();
boolean[] isPrime = new boolean[N];
for (int i = 2; i <= n; i++) {
if (!isPrime[i]) { // 是质数
primes.add(i);
if (primes.size() == 26) break;
for (int j = i+i; j <= n; j += i) {
isPrime[j] = true;
}
}
}
System.out.println(primes);
sc.close();
}
}
4.2 排序:Arrays.sort(arr) – O(nmlogm)(⭐)
时间复杂度 O ( n m l o g m ) O(nmlogm) O(nmlogm),空间复杂度 O ( n m ) O(nm) O(nm)
说明:对变位词进行排序,同一类变位词排序后会得到相同的字符串。
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<String, List<String>>();
for (String str : strs) {
char[] array = str.toCharArray();
Arrays.sort(array);
String key = new String(array);
List<String> list = map.getOrDefault(key, new ArrayList<String>());
list.add(str);
map.put(key, list);
}
return new ArrayList<List<String>>(map.values());
}
}
4.3 计数:StringBuilder – O(nm)
时间复杂度 O ( n m ) O(nm) O(nm),空间复杂度 O ( n m ) O(nm) O(nm)
说明:记录变位词每个字符出现的次数,并将其形成字符串(eg:a2b3c1),同样同一类变位词形成的字符串一定相同。
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<String, List<String>>();
for (String str : strs) {
int[] counts = new int[26];
int length = str.length();
for (int i = 0; i < length; i++) {
counts[str.charAt(i) - 'a']++;
}
// 将每个出现次数大于 0 的字母和出现次数按顺序拼接成字符串,作为哈希表的键
StringBuffer sb = new StringBuffer();
for (int i = 0; i < 26; i++) {
if (counts[i] != 0) {
sb.append((char) ('a' + i));
sb.append(counts[i]);
}
}
String key = sb.toString();
List<String> list = map.getOrDefault(key, new ArrayList<String>());
list.add(str);
map.put(key, list);
}
return new ArrayList<List<String>>(map.values());
}
}
5. 剑指 Offer II 034. 外星语言是否排序 – P87
给定一组用外星语书写的单词 words,以及其字母表的顺序 order,只有当给定的单词在这种外星语中按字典序排列时,返回 true;否则,返回 false。
5.1 哈希表:数组模拟哈希表 – O(nm)(⭐)
时间复杂度 O ( n m ) O(nm) O(nm),空间复杂度 O ( 26 ) O(26) O(26)
class Solution {
// 1. 数组模拟哈希表
public boolean isAlienSorted(String[] words, String order) {
int[] map = new int[26];
for (int i = 0; i < order.length(); i++) {
map[order.charAt(i)-'a'] = i; // 构建哈希表,key为英文字符,value为字典顺序
}
for (int i = 0; i < words.length-1; i++) {
if (!isOrder(words[i], words[i+1], map)) {
return false;
}
}
return true;
}
public boolean isOrder(String w1, String w2, int[] map) {
int i = 0;
for (; i < w1.length() && i < w2.length(); i++) {
char c1 = w1.charAt(i);
char c2 = w2.charAt(i);
if (map[c1-'a'] < map[c2-'a']) return true; // 正确排序
if (map[c1-'a'] > map[c2-'a']) return false; // 错误排序
}
return i == w1.length();
}
}
6. 剑指 Offer II 035. 最小时间差 – P88
给定一个 24 小时制(小时:分钟 “HH:MM”)的时间列表,找出列表中任意两个时间的最小时间差并以分钟数表示。
6.1 排序:计算两两差值 + 鸽巢原理 – O(nlogn)(⭐)
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn),空间复杂度 O ( n ) O(n) O(n)
class Solution {
public int findMinDifference(List<String> timePoints) {
int n = timePoints.size();
if (n > 1440) { // 鸽巢原理
return 0;
}
int res = Integer.MAX_VALUE;
Collections.sort(timePoints);
int fp = getMinite(timePoints.get(0)); // 记录第一个元素
int prev = fp; // 通过 prev 记录前一元素
for (int i = 1; i < timePoints.size(); i++) { // 开始两两比较,记录最小值
int cur = getMinite(timePoints.get(i));
res = Math.min(res, cur - prev);
prev = cur;
}
res = Math.min(res, fp + 1440 - prev); // 处理首尾 00:00
return res;
}
public int getMinite(String t) { // 获取时间转换的分钟值
return ((t.charAt(0) - '0') * 10 + t.charAt(1) - '0') * 60 + (t.charAt(3) - '0') * 10 + t.charAt(4) - '0';
}
}