【前缀和】【差分】|一维前缀和|二维前缀和|一维差分|二维差分|详解

一，前缀和

1,前缀和思想

前缀和是一种简单的思想，首先我们以一维前缀和为例子，他被用来对一段区间的快速求解，当我们要求解一段区间的时候，我们很可能要多次遍历，从而使时间复杂度达到O(n)，但是当这个算法是要查询M次的时候，我们时间复杂度就会加速上升，那么我们优美有一种简单的方法降低一下这个时间复杂度呢？

我们在求解在区间 【n,m】 这个区间的时候，我们可以使用朴素算法中使用a_m+a_m-1+…+a_n 这个思路来完成对这个区间的朴素求解，现在我们要优化一下这个过程，我们可以在读入数组的时候，也创建一个求前n个和的数组，我们使用这个数组工具和S_[m] - S_[n] 这个思路来完成这个区间的求解。

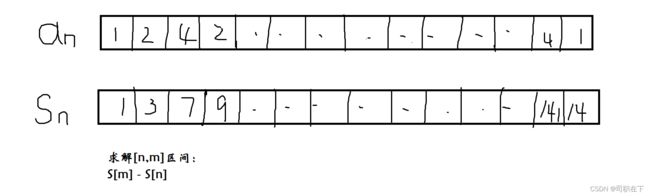
然后我们再来看二维前缀和，二维前缀和相对于一维前缀和是比较复杂的 ，我们也可以把二维数组想象成矩阵的样子，我们可以对这个矩阵求解一个前缀和矩阵，这个前缀和的求解方式是一种思想，我们在下面这张图中可以知道，我们想要求解A1区域的前缀和，首先我们要用这个A2 + A3 -A4 +D1 这个思路求解，D1是这个点的值。这样就能完成二维数组的构建过程了
完成数组的构建过程之后我们怎么求解他在一定区域中的值呢？

我们可以通过这种模拟操作来完成二维前缀和使用时候的处理，二维前缀和在使用的时候，只需要按照A1 +A2 -A3 -A4 这个公式完成对数值的求解操作。

2，前缀和的代码实现

一维前缀和的实现：就是简单的按照上文的算法思路来简单的写一下，输出的时候要注意一下，这个输出的操作为 **S[x] - S[y - 1] ** 的操作.

#include 
using namespace std ;
const int N = 100010 ;

int q[N] , s[N] ;
//存储该点的数值的q[N]数组，存储前缀和的s[N]数组
int main ()
{
    int n , m ;
    cin >> n >> m ;
    for(int i = 1 ; i <= n ; i ++ )
    {
        cin >> q[i] ;
        s[i] = s[i - 1] + q[i] ;
    }
    //完成两个数组的建立
    while ( m -- )
    {
        int x , y ;
        cin >> x >> y ;
        cout << s[y] - s[x - 1] << endl; 
    }
    return 0 ;
}

二维前缀和：我们需要注意的一点就是防止数组越界问题的出现，我们一般情况下从下标1开始存储操作，而不是下标0。

#include 
using namespace std ;

const int N = 1010 ;

int q[N][N] , s[N][N] ;


int main ()
{ios::sync_with_stdio(0);
    int n , m , cnt ;
    cin >> n >> m >> cnt ;
    for(int i = 1 ; i <= n ; i ++ )
        for(int j = 1 ;j <=m ;j ++ )
            cin >> q[i][j] ;
//完成q数组的构建
        for(int i = 1 ; i <= n ; i ++ )
        for(int j = 1 ;j <=m ;j ++ )
            s[i][j] = s[i - 1][j] + s[i][j -1] + q[i][j] - s[i - 1][j - 1] ;
//完成s数组的构建
        while (cnt -- )
            {
                int x1, x2, y1 , y2 ;
                cin >> x1 >> y1 >> x2 >> y2 ;
                cout << s[x1 - 1][y1 - 1] + s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] << endl ; 
            }

    return 0 ;
}

二，差分算法

1,差分算法思路

差分算法就是为了解决区间操作，前缀和是为了解决区间求和，所谓差分也是开一个相关的数组，存储这一位数和上一位数的差值，从而进行相关的操作。首先是一维前缀和，我们只用q[n] - q[n -1] 来完成数组的存储操作，在我们进行区间操作，【n,m】 区间内加上 x 这个操作的时候，我们的思路是 c[n] += x , c[m + 1] -= x 。当我们输出这个数组的时候我们用逐步相加就能输出，

二维差分数组就相对的比较复杂，二维差分不能像二维前缀和一样思考，这两个可以说是两个不同思路的东西，二维差分数组是对向后的操作，首先两个相加的数组是a[x1][y1] 和 **a[x2 + 1][y2 + 1] ** ,相减的操作是对极大的加的操作，我们可以看下面这个数组

基本上算是完美的诠释了这个差分的操作,这个诠释了，差分矩阵的读入操作，但是他没有完成他的输出操作，他的输出操作应当是 加两边减对角线上类似前缀和的操作.

2，差分算法的实现

一维差分算法

#include 
using namespace std ;

const int N  =100010 ;

int q[N] , k[N] ;

int main ()
{
    int n , m ;
    cin >> n >> m;
    for(int i = 1 ; i <= n ;i ++ )
    {
        cin >> q[i] ;
        k[i] = q[i] - q[i - 1] ;
    }

    //完成原数组和差分数组的赋值操作
    while ( m -- )
    {
        int x ,y , z ;
        cin >> x  >> y >> z;
        //核心步骤
        k[x] +=z ;
        k[y + 1] -= z ;
        //以上两步
    }
    int cnt = 0 ;
    for(int i = 1 ; i <= n ; i ++ )
        {
            cnt +=k[i];
            cout << cnt << " ";
        }
    return 0 ;
}

二维差分算法

#include 

using namespace std ;

const int N = 1010 ;

int q[N][N] , k[N][N] ;

void insert (int x1 ,int y1 ,int x2 ,int y2 ,int z)
{
    k[x1][y1] += z; 
    k[x2 + 1][y2 + 1] += z ;
    k[x2 + 1][y1] -= z ;
    k[x1][y2 + 1] -= z ; 
}

int main ()
{
    int n , m , p ;
    cin >> n >> m >> p;
    for(int i = 1 ; i <= n ; i ++ )
        for(int j = 1 ; j <= m ; j ++ )
            {cin >> q[i][j] ;
            insert(i , j , i , j,q[i][j]);
            }
        while (p --)
        {
            int x1 ,y1, x2 ,y2 ,cnt ;
            cin >> x1 >> y1 >> x2 >> y2 >> cnt ;
            insert(x1 ,y1 ,x2 ,y2 ,cnt );
        }
        for(int i = 1 ;i <= n ;i ++ )
           { for(int j = 1 ;j <= m ;j ++ )
            {
                k[i][j] +=  k[i - 1][j] + k[i][j - 1]- k[i -1 ][j - 1];
                cout << k[i][j] << " ";
            }
            cout << endl; 
        }
    return 0 ;
}

三，两种算法的思考

无论是差分算法还是前缀和算法，他们都注重的是通过一个数组工具来完成这个算法的操作，我们只要熟练的掌握这些数组的创建，区间使用，输出操作就能完成这些算法的理解.同时前缀和和差分数组是相反的，所以前缀和的创建实际上就相当于差分的输出 （进阶版本，要对差分数组进行赋值） 同时差分的创建也和前缀和的输出类似 （不完全一致）

四，算法竞赛中的前缀和和差分

思想

前缀和 ： 前缀和问题是用来解决对小区间进行加减等操作的操作。
差分： 是用来解决