Strange Towers of Hanoi 汉诺塔问题及其升级（递推）四个汉诺塔问题

今天学习递推的汉诺塔问题，非常的有趣

1、汉诺塔问题来源

汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

分析

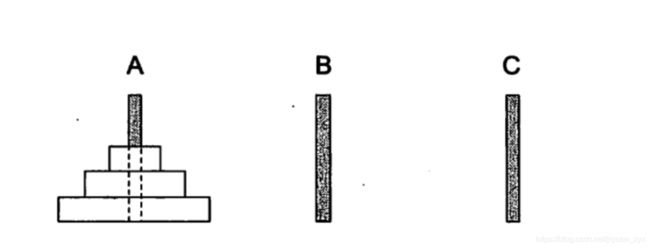
有三根柱子（A，B，C）。A柱子上面套着n个圆盘。这些圆盘大小各异，按从小到大的顺序自上而下摆放。

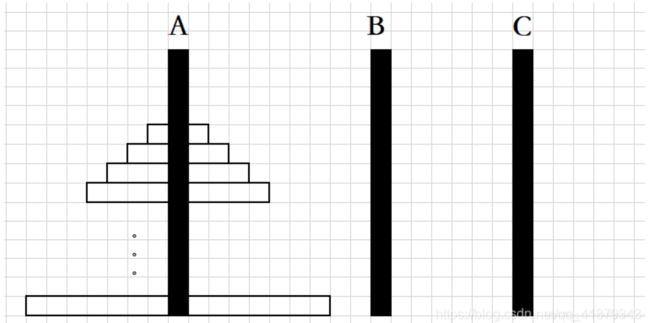
现在要把套在A柱上的n个圆盘全部移动到B柱上。并且移动圆盘时必须遵守下述规则：

一次只能移动柱子最上端的一个圆盘。
小圆盘上不能放大圆盘。
将一个圆盘从一根柱子移到另一根柱子，算是移动1次，那么，将n个圆盘全部从A移动到B至少需要移动几次呢？
首先：我们应该先从小汉诺塔入手。
一开始就考虑n个圆盘的话头脑会混乱，所以我们先缩小问题的规模，从3个圆盘开始思考。
即：暂时不考虑n个圆盘的问题，而是先找出3个圆盘的“3层汉诺塔”的解法。

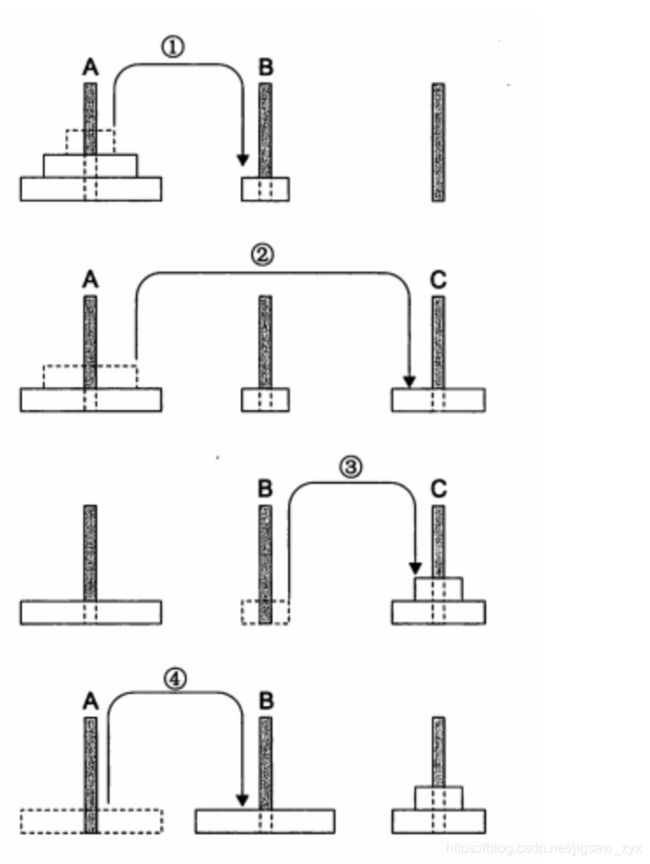
经过尝试我们可以得到“3层汉诺塔”的解法，移动7次即可解决问题，即：

仔细观看这个移动过程，我们仿佛在做“重复且相似的事情”。之所以会有这种感觉是因为我们看到了一丝规律：
我们仔细看看图中①②③和⑤⑥⑦的移动过程：

①②③中，移动3次将2个圆盘从A柱移动到了C柱。
⑤⑥⑦中，移动3次将2个圆盘从C柱移动到了B柱。
再仔细看看移动2个圆盘的规律：

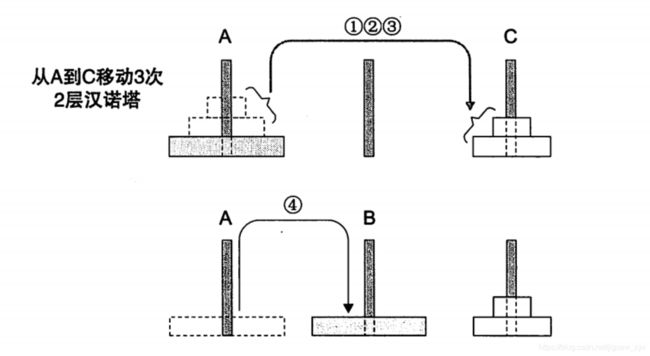
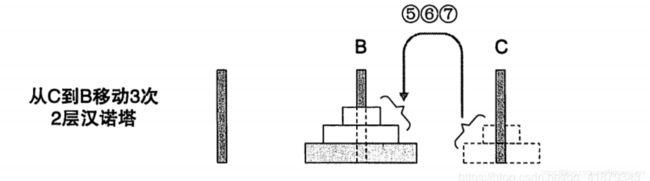
虽然移动的目的地不同，但是这两个行为动作却是非常相似的。而这种“移动2个圆盘”的动作不就是“2层汉诺塔”的解法吗。
用同样的思路我们可以进一步解决“5层汉诺塔”的问题，即：

首先，将4个圆盘从A柱移到C柱（解出4层）
然后，将（5个中）最大的圆盘从A柱移到B柱
最后，将4个圆盘从C柱移到B柱（解出4层）
“4层汉诺塔”，“3层汉诺塔”“2层汉诺塔”…也是用同样的解法。当然“1层汉诺塔”只需要移动一次圆盘就完成了。
通过这种方式我们可以总结出n层汉诺塔的解法：
我们用x,y,z来分别代表起点柱，目标柱，中转柱。注意：x,y,z并不具体代表A,B,C柱子，在不同情况下会不固定的对应A,B,C中的某一个。
解决n层汉诺塔的步骤，即：利用z柱将n个圆盘从x柱转移至y柱。
将n个圆盘从x柱，经由z柱中转，移到y柱时：

当n=0时：

• 不做任何操作
  当n>0时：
• 首先，将n-1个圆盘从A柱移到C柱（解出n-1层）
• 然后，将（n个中）最大的圆盘从A柱移到B柱
• 最后，将n-1个圆盘从C柱移到B柱（解出n-1层）
  由以上步骤可知：为了解出n层汉诺塔，要使用n-1层汉诺塔的解法。
  那么，我们可以用H(n)表示解出n层汉诺塔所需的最少移动次数。
  当n=0时，H(0)=0;
  当n=1时，H(1)=1;
  当n=2时，H(2)=H(1) + 1 + H(1) = 3;
  当n=3时，H(3)=H(2) + 1 + H(2) = 7;
  。
  。
  。
  最终我们可以得到：
  

即：

这就是我们这个问题的递推公式。
当然，仔细的朋友已经发现：
0 = 1 - 1；
1 = 2 - 1；
3 = 4 - 1；
7 = 8 - 1；
。。。
即：H(n) = 2^n - 1;

————————————————
以上是转自一篇很好的博客，由于它太好了，我觉得没有必要自己再写了，原文链接：

https://blog.csdn.net/qq_41879343/article/details/88671673

下面进入第二个精彩部分：

2、Strange Towers of Hanoi【DP】【递推】

题目大意：

将汉诺塔中的3跟柱子改为4根，求盘子数为1到12时将全部盘子从第一根移动到最后一根需要移动的次数。
传统的3给汉诺塔的方程是：

f[i]=f[i−1]×2+1

那么我们要怎么利用它得到四个的呢？

思考

题目链接：

https://ac.nowcoder.com/acm/contest/998/E

传统的汉诺塔告诉我们，汉诺塔最重要的就是大问题化小问题，小问题直接解决，那么我们如何将四个汉诺塔问题转换为3个的问题呢？

其实很简单，首先，如果我们从第一个汉诺塔中取出j个盘子到第二个汉诺塔中，并将这j个盘子（也就是第二个塔）固定不看，就只看第一个塔剩下的n-j个盘子，这样就把四个汉诺塔问题转换成了三个。然后我们又把固定在第二个塔中的j给盘子转移到D盘就可以了。

然后我们仔细来想：

首先，从A柱取出j个盘子转移到B柱，我们把下面的n-j个蒙住不看，这j个盘子面临的汉诺塔也将是四个汉诺塔问题，我们又可以将j再进行二分，直到分到分出来的盘子为1或者2时，我们再递归回去j个盘子的情况。可见这一步是明显的递归过程。

接着，将第一个塔中的n-j个盘子移到第四个，由于第二个塔固定，直接按三个汉诺塔问题来求解，这样，就可以啦！

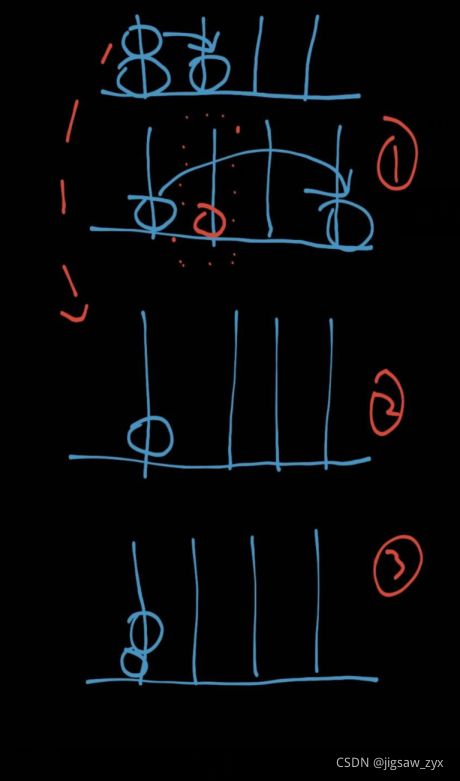
图示，大约如下：

解题步骤：

1.从A柱子中取出j个盘子移到B柱子，固定B柱子

2.剩下的n-j个按照三汉诺塔移到D柱子

 f[4][n]=f[4][j]*2+f[3][n-j]

3.找到当取出j个盘子时，移动这n个盘子的次数最小的情况

 f[4][n]=min（f[4][j]*2+f[3][n-j],f[4][n]);

4.将移出的j个柱子单独看，可以发现它是四个汉诺塔问题，重复1、2、3步

f[4][1]=1

for (int i=2;i<=n;i++)
 {
      for (int j=1;j<=i;j++)
         f[4][i]=min(f[4][j]*2+f[3][i-j],f[4][i]);
    }

…

解决问题。
AC代码

#include
#include
#include
#include
#define Inf 1e9
using namespace std;

int f[5][15];

int main(){
    f[3][1]=f[4][1]=1;
    for(int i=2;i<=12;i++){
        f[3][i]=2*f[3][i-1]+1;
        f[4][i]=Inf;
    }
    cout<<1<<endl;
     for (int i=2;i<=12;i++)
    {
        for (int j=1;j<=i;j++)
         f[4][i]=min(f[4][j]*2+f[3][i-j],f[4][i]);
        printf("%d\n",f[4][i]);
    }
    return 0;
}