leetcode刷题(柠檬水找零、接雨水、宝石与石头、将数组和减半的最少操作次数、更新数组后处理求和查询、删除每行中的最大值、并行课程③)
目录
1、柠檬水找零
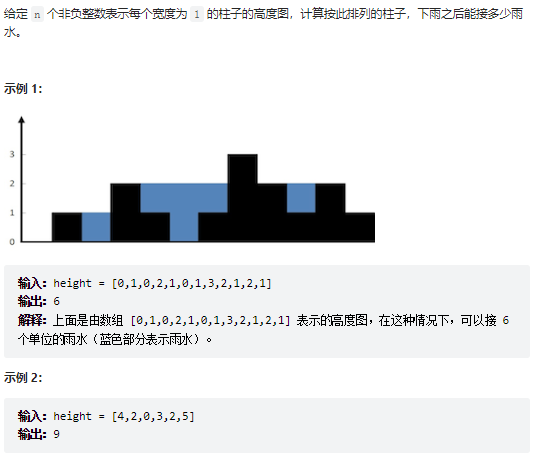
2、接雨水
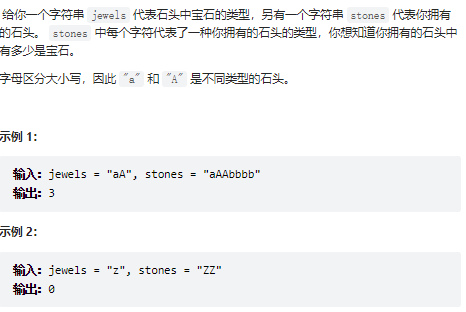
3、宝石与石头
4、将数组和减半的最少操作次数
5、更新数组后处理求和查询
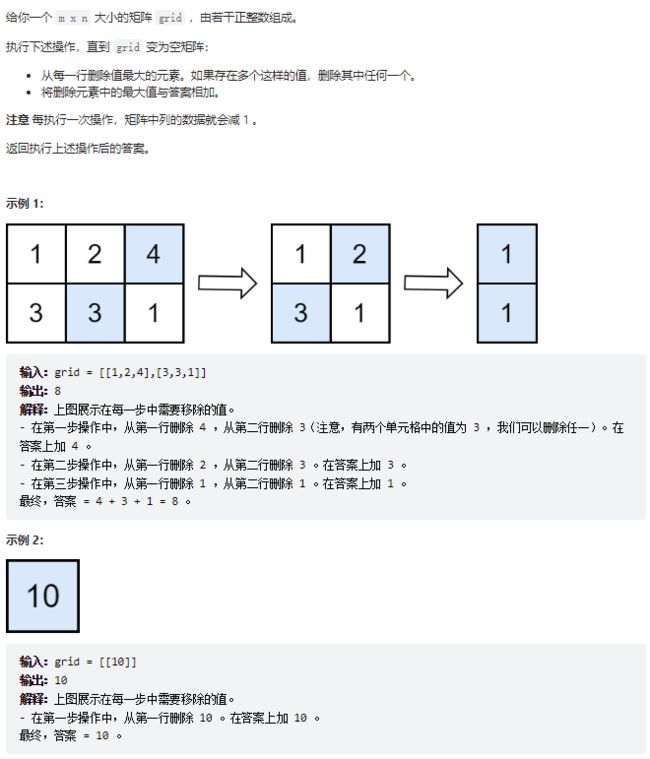
6、删除每行中的最大值
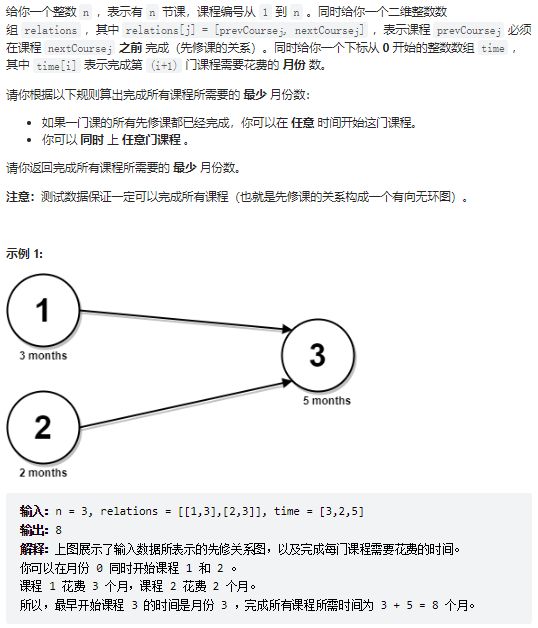
7、并行课程③
1、柠檬水找零
class Solution:
def lemonadeChange(self, bills: List[int]) -> bool:
dollars = [0, 0] # 美元数组,第一个数字记录5美元的数量,第二个数字记录10美元的数量
for bi in bills:
if bi == 5:
dollars[0] += 1 # 顾客给了5美元,无需找零,5美元数量加一
elif bi == 10:
if dollars[0] < 1: return False # 顾客给了10美元,但没有5美元的零钱找,无法找零
dollars[0] -= 1 # 可以找零,5美元数量减一
dollars[1] += 1 # 10美元数量加一
else:
if dollars[1] > 0 and dollars[0] > 0:
# 20美元优先用一张10美元和一张5美元找零
dollars[0] -= 1
dollars[1] -= 1
elif dollars[0] >= 3:
# 否则用三张5美元找零
dollars[0] -= 3
else:
# 否则无法找零
return False
return True2、接雨水
class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
left_max = [0] * n # 位置i左侧(包含i)大于等于height[i]的最大值
right_max = [0] * n # 位置i右侧(包含i)大于等于height[i]的最大值
left_max[0] = height[0] # 最左侧的端点的最大值为它本身
right_max[-1] = height[-1] # 最右侧的端点的最大值为它本身
for i in range(1, n):
# 同时生成两个数组
left_max[i] = max(left_max[i - 1], height[i])
right_max[-(i + 1)] = max(right_max[-i], height[-(i + 1)])
ans = 0
for l, r, h in zip(left_max, right_max, height):
ans += min(l, r) - h # 位置i的雨水量取决于两侧最大值中的较小值与height[i]的差
return ans
3、宝石与石头
class Solution:
def numJewelsInStones(self, jewels: str, stones: str) -> int:
count = 0
for s in stones:
if s in jewels:
count += 1
return count4、将数组和减半的最少操作次数
class Solution:
def halveArray(self, nums: List[int]) -> int:
sum1 = sum(nums) #首先利用sum函数将数组元素求和
target = sum1 / 2 #其次算出要得到的目标值,即原数组和的一半
queue = [] #定义一个优先权队列备用
for num in nums:
heapq.heappush(queue, -num) #heapq实现的是最小堆,在本题中要实现最大堆,将元素取法异曲同工
count = 0 #记录减少一半的次数
while sum1 > target:
num = heapq.heappop(queue) / 2 #heappop取出来的是堆顶,此时是负数,将其变为一半
sum1 += num #因为是取的相反数,所以此处直接相加即为在原数组和上减去这个值的一半
heapq.heappush(queue, num) #最大元素减半以后放回队列
count += 1
return count
# import heapq
# queue = []
# nums = [12, 34, 1, 5]
# for num in nums:
# heapq.heappush(queue, num)
# print(queue)
# a = heapq.heappop(queue)
# print(a)
#这是对于heapq.push和heapq.pop用法解释
#最终输出queue为[1,5,12,34], a为15、更新数组后处理求和查询
class Node:
def __init__(self):
self.l = self.r = 0
self.s = self.lazy = 0
class SegmentTree:
def __init__(self, nums):
self.nums = nums
n = len(nums)
self.tr = [Node() for _ in range(n << 2)]
self.build(1, 1, n)
def build(self, u, l, r):
self.tr[u].l, self.tr[u].r = l, r
if l == r:
self.tr[u].s = self.nums[l - 1]
return
mid = (l + r) >> 1
self.build(u << 1, l, mid)
self.build(u << 1 | 1, mid + 1, r)
self.pushup(u)
def modify(self, u, l, r):
if self.tr[u].l >= l and self.tr[u].r <= r:
self.tr[u].lazy ^= 1
self.tr[u].s = self.tr[u].r - self.tr[u].l + 1 - self.tr[u].s
return
self.pushdown(u)
mid = (self.tr[u].l + self.tr[u].r) >> 1
if l <= mid:
self.modify(u << 1, l, r)
if r > mid:
self.modify(u << 1 | 1, l, r)
self.pushup(u)
def query(self, u, l, r):
if self.tr[u].l >= l and self.tr[u].r <= r:
return self.tr[u].s
self.pushdown(u)
mid = (self.tr[u].l + self.tr[u].r) >> 1
res = 0
if l <= mid:
res += self.query(u << 1, l, r)
if r > mid:
res += self.query(u << 1 | 1, l, r)
return res
def pushup(self, u):
self.tr[u].s = self.tr[u << 1].s + self.tr[u << 1 | 1].s
def pushdown(self, u):
if self.tr[u].lazy:
mid = (self.tr[u].l + self.tr[u].r) >> 1
self.tr[u << 1].s = mid - self.tr[u].l + 1 - self.tr[u << 1].s
self.tr[u << 1].lazy ^= 1
self.tr[u << 1 | 1].s = self.tr[u].r - mid - self.tr[u << 1 | 1].s
self.tr[u << 1 | 1].lazy ^= 1
self.tr[u].lazy ^= 1
class Solution:
def handleQuery(
self, nums1: List[int], nums2: List[int], queries: List[List[int]]
) -> List[int]:
tree = SegmentTree(nums1)
s = sum(nums2)
ans = []
for op, a, b in queries:
if op == 1:
tree.modify(1, a + 1, b + 1)
elif op == 2:
s += a * tree.query(1, 1, len(nums1))
else:
ans.append(s)
return ans
6、删除每行中的最大值
class Solution:
def deleteGreatestValue(self, grid: List[List[int]]) -> int:
for row in grid:
row.sort() # 对每一行进行排序
score = 0 # 分数初始为0
for j in range(len(grid[0])):
col_max_val = grid[0][j] # 初始化每一列最大值为该列首行的值
for i in range(len(grid)):
col_max_val = max(grid[i][j], col_max_val) # 找到每一列的最大值
score += col_max_val
return score
7、并行课程③
class Solution:
def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:
g = defaultdict(list)
indeg = [0] * n
for a, b in relations:
g[a - 1].append(b - 1)
indeg[b - 1] += 1
q = deque()
f = [0] * n
ans = 0
for i, (v, t) in enumerate(zip(indeg, time)):
if v == 0:
q.append(i)
f[i] = t
ans = max(ans, t)
while q:
i = q.popleft()
for j in g[i]:
f[j] = max(f[j], f[i] + time[j])
ans = max(ans, f[j])
indeg[j] -= 1
if indeg[j] == 0:
q.append(j)
return ans