检错纠错码(奇偶校验码 CRC循环冗余校验码 海明码)
检错与纠错码在计算机中经常被使用,在此对常用的三种检错纠错码做一个介绍,分别是奇偶校验码,CRC循环冗余校验码和海明码。
奇偶校验码
通常所说的奇偶校验码指的是一维奇偶校验码,它只能检错,不能纠错;只有二维奇偶校验码具备纠错能力。
校验方法:分为奇校验和偶校验,默认是校验所传输数据中’1’的个数是奇数还是偶数。
当约定为奇校验时,当所传输数据中’1’的个数为奇数,便在数据后面添加’0’;当所传输数据中’1’的个数为偶数,便在数据后面添加’1’,使1的个数满足奇数个。当约定为偶校验时,类似。后面的附加位选择是用来控制数据中’1’的个数,使其满足校验规则(奇数个或是偶数个)。
判断是否出错?当约定为奇校验时,如果接收方收到的数据中’1’的个数为奇数时,则认为未出错,否则发生错误。偶校验时类似。
例如:对待传输数据10110110约定采用奇校验时,发送方所需要发送的校验码为101101100,对于接收方来说,如果接收到的数据中’1’的个数不为奇数时,就会认为数据出错。
特点:接收方不会知道是数据的哪一处发生错误;只能检测奇数个位出现错误的情形,不能检验偶数个位发生错误;开销小,常用来校验1字节长的数据(只有1位出现错误的可能性大)。
CRC循环冗余校验码
循环冗余校验可以发现并纠正信息在传输过程中所出现的错误。
由于后面计算的需要,先引入模2运算的计算方法,它也可以看作为异或运算。
模2加法-按位加,不考虑进位:0+0=0;0+1=1;1+0=1;1+1=0。模2减法-按位减,不考虑借位:0-0=0;0-1=1;1-0=1;1-1=0。可以看出模2加法与减法的运算结果相同,故一律采用模2加法来运算。模2乘法-按照模2加法求部分积之和,不考虑进位。模2除法-按照模2减法求部分余数,不借位。余数的位数应该为除数的位数减一。
生成多项式:G(x)的选用需要满足合适的条件:1,任何一位发生错误,都应该使余数不为0;2,不同位发生错误应使余数不同;3,对余数继续做模2除,应使余数循环。当然,在实际中只需查找资料来选用我们需要的生成多项式即可。
常用的3阶4位生成多项式G(x)为x³+x+1,转换成二进制为1011。
校验方法:将所给的k位生成多项式看作为除数(提示:被除数/除数=商),将所传输的数据左移k-1位,除以生成多项式得到一个k-1位的余数。再将左移过的所传输数据与所得的余数相加,相加的结果就为CRC码。CRC码左边的k-1位称为校验位,其余称为有效信息位。
判断是否出错?如果接收方收到的数据除以G(x)的余数为0(即能被G(x)整除),则认为未出错,如果不能被整除,则认为在传输过程中发生错误,并由所得的余数指出哪一位出错,从而进行纠正。
例如:若有效信息为1100,用生成多项式G(x)=1011将其编成CRC码的过程如下。
首先发现G(x)为4位,从而将有效信息1100左移3位,得1100000,再用它除生成多项式,即1100000/1011=1110…010,所得余数010与被除数1100000相加,得1100010,这便是我们所求得的CRC码。
其中关于模2除法如下图:
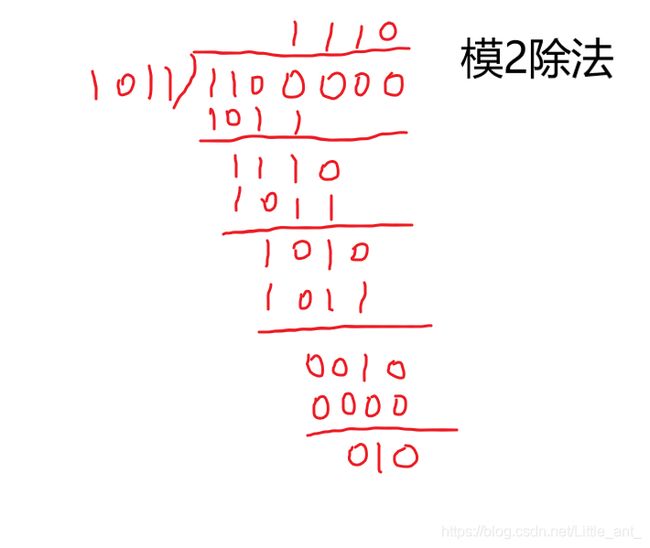
关于接收方的出错模式如下(其中G(x)=1011 ):
| CRC码序号 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 余数 | 出错位置 |
|---|---|---|---|---|---|---|---|---|---|
| 正确CRC码 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 000 | 无 |
| 出错: | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 001 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 010 | 1 | |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 100 | 2 | |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 011 | 3 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 110 | 4 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 111 | 5 | |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 101 | 6 |
如果CRC码中有一位出错,就会得到一个不为0的余数。如果将余数左移一位继续除下去,会发现各次所得余数将按照上表所示的顺序循环。例如位置0出错,余数为001,将其左移得到0010,再除以G(x)得余数010,左移得到0100,除以G(x)得余数100…反复循环,这便是“循环码”名称的由来。
对于不同的二进制数来讲,
如果我们所选的生成多项式不变,那么所得的余数与出错位置的对应关系也不会
变。
即如果有效信息为1001时,它通过G(x)=1011所得到的CRC码为1001110,对于接收方来讲,如果第0位出错,余数依然为001,第1位出错,余数依然为100…
4位的生成多项式最多可传输多少位有效信息
当生成多项式为1011(4位,最高次幂为3),校验位为3位时,所得余数的位数也只能为3,它可能会出现2^3=8种不同的排列结果,其中去掉传输成功时的余数000,还剩余7种不同的结果,它刚好可以对应传输数据种7种不同位的出错可能(4个有效信息位和3个校验位)。如上例的4位有效信息1100,这也是采用4位生成多项式为1011所能传输的最大有效信息位。
如果当有效信息为5位时,生成多项式仍为1011,所得CRC码为8位,而3个校验位最多只能检测出7种不同位的错误,需要增加校验位,即需要采用更高阶的生成多项式。
结论:4位的生成多项式最多可传输4位有效信息
特点:纠正1位错误;检验1位或2位错误;检验所有奇数位错误;检验低于16位的突发性错误;对高于16位的突发性错误的检测成功率高达99.9%。
海明码
引入:如果对n位数据增加k位检测位,使得通过检测位可以发现并纠正错误。那么n与k之间需满足的关系是 2^k≥n+k+1。
这个不等式与CRC码最后问题所得到的结论是相同的,当k为3时,2的3次方为8,故所取的数据位数n最大为4,在此不做赘述。唯一的区别是海明码的校验位是分散在有效信息位中的。通过不等式2^k≥n+k+1所得到的代码长度与检测位的关系如下:
| n | k |
|---|---|
| 1 | 2 |
| 2~4 | 3 |
| 5~11 | 4 |
| 12~26 | 5 |
| 27~57 | 6 |
| 58~120 | 7 |
关于汉明码的编码方法,在这里就不列举公式了(公式很长)。下面通过举例来说明海明码的构造和检错方法:
例:在海明校验中采用偶校验,对有效信息01001101进行海明编码。
首先,有效信息位个数n=8,通过上面的不等式得出校验位的个数应该为4,所以海明码应该为8+4=12位。列表如下
| 内容 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 编号 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
其中4个校验位分别位于编号为‘8’ ‘4‘ ‘2’ ’1‘处,如果有更多的校验位,编号可以继续取’16‘ ’32‘ ’64‘…;8位有效信息码依次填入其余编号处,至此第一步完成。
然后通过下面12个等式,用校验位编号表示出海明码所有的编号‘1’-‘12’
1=1 2=2 3=1+2 4=4 5=4+1 6=4+2 7=4+2+1 8=8 9=8+1 10=8+2 11=8+2+1 12=8+4在上述等式中
右边含有编号为’1’的校验位有’3’,‘5’,‘7’,‘9’,‘11’。对这5位上的内容做偶校验,可得’1‘校验位的内容应该为1,从而使得编号‘1’,‘3’,‘5’,‘7’,‘9’,'11’中的数据满足偶校验。可认为这5位中的数据是由‘1’校验位来负责。
| 内容 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 编号 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
右边含有编号为‘2’的校验位有‘3’,‘6’,‘7’,‘10’,‘11’。对这5位上的内容做偶校验,可得‘2’校验位的内容应该为0,从而使得编号‘2’,‘3’,‘6’,‘7’,‘10’,‘11’中的数据满足偶校验。可认为这5位中的数据是由‘2’校验位来负责。
| 内容 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 编号 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
右边含有编号为‘4’的校验位有‘5’,‘6’,‘7’,‘12’。对这4位上的内容做偶校验,可得‘4’校验位的内容应该为0,从而使得编号‘4’,‘5’,‘6’,‘7’,‘12’中的数据满足偶校验。可认为这4位中的数据是由‘4’校验位来负责。
| 内容 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 编号 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
右边含有编号为‘8’的校验位有‘9’,‘10’,‘11’,‘12’。对这4位上的内容做偶校验,可得‘8’校验位的内容应该为1,从而使得编号‘8’,‘9’,‘10’,‘11’,‘12’中的数据满足偶校验。可认为这4位中的数据是由‘8’校验位来负责。
| 内容 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 编号 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
由此就得到在满足偶校验下的对应于信息01001101的海明编码为010011100101.
对上面的海明码,如果编号‘6’中的数据出错,接收方如何知道是数据种的哪一位出错呢?
接收方所得到的编码如下:
| 内容 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 编号 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
检错:
对于校验位‘1’,由于是偶校验,而‘1’所负责的编号‘1’,‘3’,‘5’,‘7’,‘9’,'11’中的数据满足101011偶校验,正常。
对于校验位‘2’,由于是偶校验,而‘2’所负责的编号‘2’,‘3’,‘6’,‘7’,‘10’,‘11’中的数据101010不满足偶校验,故‘2’所负责的几位中有一位出错。
对于校验位‘4’,由于是偶校验,而‘4’所负责的编号‘4’,‘5’,‘6’,‘7’,‘12’中的数据01000不满足偶校验,故‘4’所负责的几位中有一位出错。
对于校验位‘8’,由于是偶校验,而‘8’所负责的编号‘8’,‘9’,‘10’,‘11’,‘12’中的数据01001满足偶校验,正常。
据此可得,发生错误的位置编号为4+2=6,即编号‘6’处数据发生错误,从而进行改正。
特点:可以检测出2位错误,纠正1位错误。