树与图c++
1.树
前言
本文主要介绍的数据结构之树型结构的相关知识,树型数据结构是面试官面试的时候非常喜欢考的一种数据结构,树形结构的遍历也是大厂笔试非常喜欢设置的考点,这些内容都会在本篇文章中进行详细的介绍,并且还会介绍一些常用的算法。
一、树的基本概念
层次结构的数据在现实世界中大量存在。例如,一个国家有若干省,一个省有若干市县,一个市县有若干区乡。又如,一本书包含若干章,一章包含若干节,一节包含若干段。例如,下图是数组的层次关系,这种描述树形数据的形式称为倒置的树形表示法。
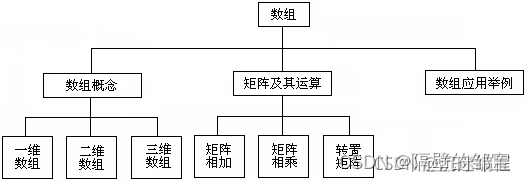
线性数据结构一般不适合用来表示层次数据。为了组织层次数据,需要对树形数据的结构进行研究。
1.1树的定义
在上图1中,我们采用倒置树来描述树状结构。一棵倒置树的顶端是根,根有几个分枝,称为子树,每棵子树再分成几个小分枝,小分枝再分成更小的分枝,每个分枝也都是树,一个结点也是树。由此,我们可以给树下一个递归定义。
树(Tree)是包括n个结点的有限非空集合T,其中,一个特定的结点r称为根(Root),其余结点T-{r}划分成m个互不相交的子集T1,T2,Tm其中,每个子集都是树,称为树根r的子树。
根据树的定义,一个结点的树是仅有根结点的树,这时m=0,这棵树没有子树。
1.2基本术语
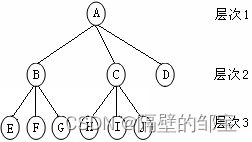
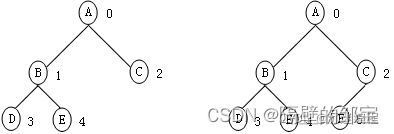
图1可以抽象成图2,它形象地反映了树的逻辑结构。下面,参照图2,给出树结构讨论中常用的术语。
树中元素称为结点(Node),如A、B等。
如果某结点到另一结点之间存在着连线,则称此连线为一条边(Edge),如
如果从某个结点沿着树中的边可到达另一个结点,则称这两个结点间存在一条路径(Path),如结点A到结点J,存在路径{
如果一个结点有子树,则称该结点为子树的双亲(Parent),子树的根称为该结点的孩子(Child),如结点A是结点B、C、D的双亲,而结点B、C、D是结点A的孩子。具有相同双亲的结点称为兄弟(Sibling),如结点B、C、D是兄弟。
结点拥有的子树数目称为结点的度(Degree),如结点A的度为3,结点D的度为0,结点J的度为0。
度为零的结点称为叶子(Leaf)。
规定根结点的层次为1,树中结点的最大层次称为该树的高度(Hight),如图2所表示的树的高度为3。
如果树中结点的各子树是从左至右有次序的,则称该树为有序树,否则称为无序树。
二、二叉树
树结构和自然界的树一样,具有各种各样的形态,这样就使我们对树结构的研究比较困难。为此,我们首先研究最为常见的二叉树,以及二叉树的性质、存储结构和运算,然后给出二叉树和一般树之间的转换。
2.1二叉树的定义
二叉树(Binary Tree)是由有限个结点组成的集合,它或者为空集合,或者仅含一个根结点,或者由一个根结点和两棵互不相交的左、右子树组成。
必须指出,树定义与二叉树定义稍有区别。首先,树不能是空树,却可以有空二叉树。其次,一般树的子树的不分次序,而二叉树的子树却分左、右子树,即使在仅有一棵子树的情况下也要指明是左子树还是右子树。最后,一般树中结点的度(子树数目)可以大于2,但二叉树中结点的度均不超过2。
2.2二叉树的性质
若二叉树高为h,树的结点总数为2^h-1,称此二叉树为满二叉树。
h=3,那么结点总数7(包含根节点)
【性质1】高度为h的二叉树的结点总数n<=2^h-1。
这个性质很容易理解:
证明:对于高度为h的满二叉树,其结点总数为
它是高度为h的二叉树结点总数的最大值,故。
对于高度为h的二叉树,如果第1~h-1层构成满二叉树,而第h层的叶子结点严格按从左至右依次排列,称此二叉树为完全二叉树(如图5(a)所示)。
在图5(b)中,双亲结点C仅有右孩子G无左孩子,故它不是完全二叉树。
【性质2】对于含n(n>=1)个结点的完全二叉树(区分满二叉树),其高度 h = ⌈ l o g 2 ( n + 1 ) ⌉ h=\lceil log2(n+1) \rceil h=⌈log2(n+1)⌉ 。
eg:上述图a,n=6,那么
h = [ l o g 2 ( 6 + 1 ) ] = l o g 2 ( 8 ) = 3 h=[log2(6+1)]=log2(8)=3 h=[log2(6+1)]=log2(8)=3
【性质3】对于一棵非空二叉树,如果度为0的结点数为,度为2的结点数为,则
=+1。 (即零度结点数总比2度结点数大1)
证 设二叉树的结点数为n,度为1的结点数为n1,边数为e,则
e = n − 1 e=n-1 e=n−1
e = 2 × n 2 + n 1 e=2×n2+n1 e=2×n2+n1
n = n 0 + n 1 + n 2 n=n0+n1+n2 n=n0+n1+n2
边数等于结点数n-1 ,等于2倍的度为2的结点数+度为1的结点数。
画个树的逻辑结构图就很容易看出来。
于是n0=n2+1。
【性质4】对于含个结点的完全二叉树(区分满二叉树),按从上到下、从左到右的顺序,从0到n-1编号(如图6所示)。对于树中编号为 i ( 0 = < i < = n − 1 ) i(0=
(1)如果 i = 0 i=0 i=0,则该结点为二叉树的根;
(2)如果 2 i + 1 < n 2_i+1
(3)结点的双亲为[(i-1)/2]向下取整。(求双亲注意双亲只有一个)
2.3二叉树的ADT
ADT BinTree
数据:
0个或有限个结点组成的集合。
运算:
Create()
创建一棵空二叉树或二叉树。
IsEmpty()
若二叉树为空,则返回1,否则返回0。
PreOrder()
前序遍历二叉树。
InOrder()
中序遍历二叉树。
PostOrder()
后序遍历二叉树。
Display():
输出二叉树。
三、二叉树的存储表示
3.1二叉树的数组表示
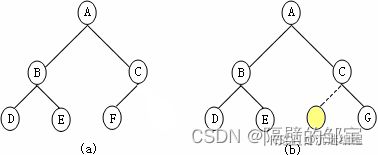
用一维数组来存储二叉树,首先将二叉树想象成一棵完全二叉树,对于没有左孩子或右孩子的结点,用特殊字符(或数字)替代,再依从上至下、从左至右的次序,依次将结点值存放到一维数组之中。
解:
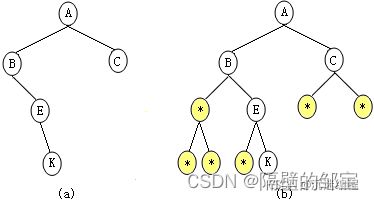
首先将图7(a)所示的二叉树,想象成一棵完全二叉树(如图7(b)所示),再用表8-1所示的一维字符型数组存储。
这种表示法的实现程序如下:示法的实现程序如下:
#include 程序运行的结果如图8所示:
创建这棵5结点二叉树,用了6颗星号替代缺失的左、右孩子,这显然是这种表示法的一个缺点。
但当二叉树为完全二叉树时,该表示法具有建树简便,输出直观的优点。
3.2二叉树的链表表示
用一维数组表示的二叉树,不便实现二叉树的一些规定运算。因此,二叉树一般采用链表来创建。
链式二叉树结点的逻辑结构如图9所示,其中,data用来存储结点值,*lChild、*rChild分别用来存储左、右孩子的地址。
图9 树节点的逻辑结构
【例2】创建图7(a)所示的链式二叉树。
用链表表示图7(a),其逻辑结构如图10所示,其中Λ代表NULL。
具体的创建过程如下:
(1)首先创建第4层结点,并用结点指针Kp指向其根结点,如图11所示。
图11
(2)再创建第3层结点,并用结点指针Ep指向其根结点,如图12所示。
图12
(3)再创建第2层结点,并用结点指针Bp、Cp分别指向其根结点,如图13所示。
图13
(4)最后创建第1层结点,并用结点指针Ap指向其根结点,如图14所示。
图14
如果用程序来描述上述过程,其程序如下:
#include上述链式二叉树的创建过程是,先创建最底层的叶子结点,然后向上逐层创建子树,直至最顶层的根结点。该方法的优点是直观易懂,缺点是无法给出通用程序。一般链式二叉树的创建方法与通用程序如下。
用广义表构建二叉树。
- 二叉树的广义表表示法
尽管构建二叉树的方法并不复杂,但对于结点多、结构复杂的二叉树,却不易用程序来实现。因此,有必要寻找更具一般性的二叉树的构建方法。
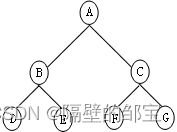
图1所示的二叉树,可以用以下方式重新表示它。
用A(B)表示A有左孩子B,无右孩子;
用B(C,D)表示B有左孩子C,右孩子D;
用C(,E)表示C无左孩子,但有右孩子E;
用D(F,G)表示D有左孩子F,右孩子G。
将它们复合起来,有A(B(C(,E),D(F,G)))。这是一个字符数组,它是上述二叉树的另一种表示法,称这种二叉树的表示法为广义表法。
用广义表来表示二叉树,其具体规定如下:
树的根结点放在最前面。
每个结点的左子树和右子树用逗号隔开。若仅有左子树没有右子树,逗号可省略;若仅有右子树没有左子树,逗号不能省略。
约定,广义表用字符型数组 GenList[] 来存储。
- 广义表构建二叉树的算法
设结点值均用字母来替代,先建一棵空二叉树T,借助一个简易结点顺序栈 stack ,广义表A(B(C(,E),D(F,G)))创建二叉树的具体过程如下:
(1)读A,创建新结点A,T为空,让T.root=A结点。
(2)读(,让新结点A入栈,置k=1,栈stack状态为:
A
(3)读B,创建新结点B,因k=1,让栈顶结点A的左指针指向B,即B←A。
(4)读(,让新结点B入栈,置k=1,栈stack状态为:
A
B
(5)读C,创建新结点C,因k=1,让栈顶结点B的左指针指向C,即C←B。
(6)读(,让新结点C入栈,置k=1,栈stack状态为:A B C
(7)读,号,置k=2。
(8)读E,创建新结点E,因k=2,让栈顶结点C的右指针指向E,即C→E。
(9)读),栈顶结点C出栈,栈stack状态为:A B
(10)读,号,置k=2。
(11)读D,创建新结点D,因k=2,让栈顶结点B的右指针指向D,即B→D。
(12)读(,让新结点D入栈,置k=1,栈stack状态为:A B D
(13)读F,创建新结点F,因k=1,让栈顶结点D的左指针指向F,即F←D。
(14)读,号,置k=2。
(15)读G,创建新结点G,因k=2,让栈顶结点D的右指针指向G,即D→G。
(16)读),栈顶结点D出栈,栈stack状态为:A B
(17)读),栈顶结点B出栈,栈stack状态为:A
(18)读),栈顶结点A出栈,栈stack状态为:
至此,二叉树创建完毕。
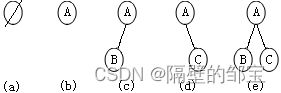
由T.root=A,B←A,C←B,C→E,可构建如下图2所示的二叉树。
图2 二叉树的构建过程1
由B→D,F←D,D→G,可构建如图3所示的二叉树。
图3 二叉树的构建过程2
3. 广义表构建二叉树算法的程序实现
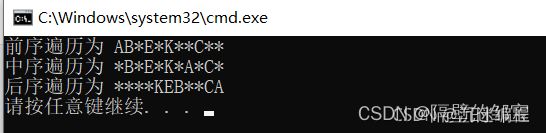
#include程序运行的结果如图4所示。
图4
四、二叉树的遍历
欲在屏幕上形象地输出链式二叉树是一件困难的事,一般采用输出它的三个线性序列VLR、LVR和LRV的方式,来解决这一问题。
VLR称为前序(PreOrder)遍历序列,它是按先树根,再左子树,后右子树的次序,输出二叉树的结点值。
LVR称为中序(InOrder)遍历序列,它是按先左子树,再树根,后右子树的次序,输出二叉树的结点值。
LRV称为后序(PostOrder)遍历序列,它是按先左子树,再右子树,后树根的次序,输出二叉树的结点值。
所谓前序、中序和后序遍历,是相对于根结点位置而言的。例如,在中序遍历中,根结点在中间;而前序遍历是根结点在前面,后序遍历是根结点在后面。三种遍历方式一定是先左子树后右子树。
4.1前序遍历
前序遍历的次序为:树根—左子树—右子树,即从根结点开始处理,根结点处理完后往左子树走,直到无法前进再处理右子树。
图10 链式二叉树的逻辑结构
【例2】的前序遍历为ABEKC,前序遍历的递归算法如下:
void PreOrder(Node *p)
{
if(p!=NULL)
{
cout<<p->data;//访问树根
PreOrder(p->lChild);//遍历左子树
PreOrder(p->rChild); //遍历右子树
}
}
4.2中序遍历
中序遍历的次序为:左子树—树根—右子树,即沿树的左子树一直往下,直到无法前进时后退到双亲结点,而后再沿右子树一直往下。如果右子树也走完了就退回上层的左结点,重复左、中、右的顺序遍历。
【例2】的中序遍历为BEKAC,中序遍历的递归算法如下:
void InOrder(Node *p)
{
if(p!=NULL)
{
InOrder(p->lChild); //遍历左子树
cout<<p->data; //访问树根
InOrder(p->rChild);//遍历右子树
}
}
【例2】的后序遍历为KEBCA,后序遍历的递归算法如下:
void PostOrder(Node *p)
{
if(p!=NULL)
{
PostOrder(p->lChild);//遍历左子树
PostOrder(p->rChild); //遍历右子树
cout<<p->data; //访问树根
}
}
#include【定理1】任意n(n>0)个不同结点的二叉树,都可由其前序遍历序列和中序遍历序列唯一确定。
【例4】画出前序遍历ABEKC,中序遍历BEKAC所确定的二叉树。
(1)由前序遍历ABEKC,A为根结点;由中序遍历BEKAC,BEK为左子树,C为右子树;其对应的二叉树如图17所示。
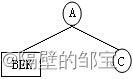
(2)对于左子树,由前序遍历BEK,B为根结点;由中序遍历BEK,EK为右子树,其对应的二叉树如图18所示。

(3)对于右子树,由前序遍历EK,E为根结点;由中序遍历EK,K为右子树,其对应的二叉树如图19所示。

五、常用二叉树
5.1排序二叉树
先给出排序二叉树的定义。
设二叉树的所有结点值互异,排序二叉树或者是一棵空树,或者是满足以下条件的树:
(1)若左子树不空,则左子树上所有结点的值均小于根结点的值;(左小于根)
(2)若右子树不空,则右子树上所有结点的值均大于根结点的值;(右大于根)
(3)左、右子树也分别是排序二叉树。(递归定义)
排序二叉树定义是由递归方式给出的,据此定义,可给出排序二叉树的创建方法:
首次输入的数据作为此二叉树的根,其后输入的数据与根进行比较,小于树根的放置到左子树,大于树根的放置到右子树。
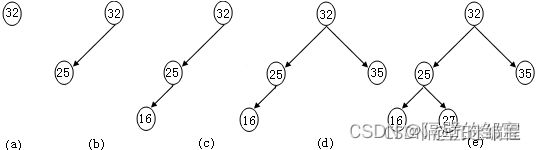
【例5】依次输入数据32,25,16,35,27,创建一棵排序二叉树。
排序二叉树的创建过程如图20所示:
创建排序二叉树的程序如下:
#include 程序运行的结果如图21所示:
排序二叉树的优点是,建树方便,中序遍历为升序序列。
5.2哈夫曼树
先介绍几个概念 。
路径长度(Path Length): 路径上的分支(边)数目。
树的路径长度(Tree Path Length): 根结点到每个叶子结点的路径长度之和。
树的带权(叶子结点的权值)路径长度(Weighted Path Length): 其中wi是第i个叶子结点的权值,li为从根结点到第i个叶子结点的路径长度,n为叶子结点的总数。
最优二叉树: WPL最小的二叉树,最优二叉树也称哈夫曼树(Huffman Tree)。
【例6】图27给出了三棵二叉树,分别计算它们的带权路径长度(即 W P L WPL WPL )。

图27 二叉树的带权路径长度
解:
(a) W P L = 9 × 1 + 15 × 2 + 3 × 3 + 4 × 3 = 60 WPL=9×1+15×2+3×3+4×3=60 WPL=9×1+15×2+3×3+4×3=60
(b) W P L = 3 × 1 + 4 × 2 + 9 × 3 + 15 × 3 = 83 WPL=3×1+4×2+9×3+15×3=83 WPL=3×1+4×2+9×3+15×3=83
(c) W P L = 4 × 1 + 15 × 2 + 9 × 3 + 3 × 3 = 70 WPL=4×1+15×2+9×3+3×3=70 WPL=4×1+15×2+9×3+3×3=70
哈夫曼给出了一个创建最优二叉树的方法。下面,我们用一个实例来介绍这一方法。
【例7】设集合{12,3,10,5,2}为叶结点的权值,试创建哈夫曼树。
创建哈夫曼树的过程,可以由以下步骤和示意图来说明。
(1)将权值按升序排序,构建单结点的二叉树集T,T如图28所示。
![]()
图28
(2)从T中选取前两棵的二叉树,分别作为左、右子树,构造一棵新二叉树(注意,排序在前的作左子树),对T中权值再按升序排序(注意,如果出现权值相等的情况,则原树排前,新树排后),T如图29所示。
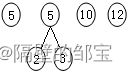
图29
(3)反复重复第(2)步的操作,T如图30 — 图32所示。

图30 创建过程3 图31 创建过程4 图32 创建过程5
必须指出,哈夫曼树的形状不唯一。但如果严格按上述规定来创建,哈夫曼树还是唯一
的,编程创建哈夫曼树将严格按上述规定进行。
性质1: 哈夫曼树不存在度为1的结点。
性质2: 设哈夫曼树的叶子结点数为 n 0 n_0 n0,则哈夫曼树的结点数 n = 2 × n 0 − 1 n=2×n_0-1 n=2×n0−1。
性质3: 哈夫曼树的带权路径长度等于所有度为2的结点值之和。