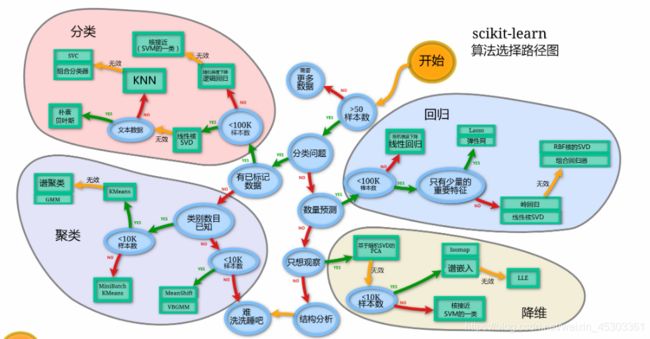
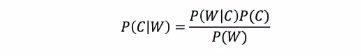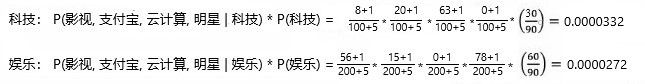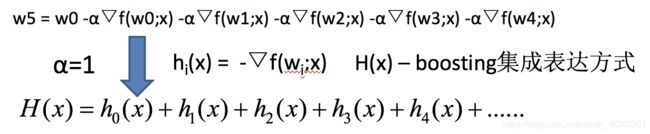经典算法 及其 API
经典算法 及其 API
- 回归算法
-
- 线型回归(Linear regression)
-
- 概念 及 回归方程
- 损失函数
- 优化算法
-
- 正规方程 及其 API
- 梯度下降 及其 API
- 正则化(岭回归 及其 API)
- 分类算法
-
- K近邻算法
-
- 算法简介 及 工作流程
- KNN算法 API (sklearn)
- 优缺点
- 朴素贝叶斯
-
-
- 贝叶斯公式 和 拉普拉斯平滑
- 朴素贝叶斯API
-
- 逻辑回归(Logistic Regression)
-
- 逻辑回归方程
- 损失以及优化
- 逻辑回归API
- 决策树
-
- 决策树分类原理
-
- 信息增益(ID3)(熵)
- 信息增益率(C4.5)(熵)
- CART 树(基尼值 和 基尼指数)
- 决策树 优化(`cart`剪枝)
- 决策树 API 及 可视化
- 聚类算法
-
- K-means
-
- k-means 聚类原理
- K-means API
- 评估模型 并 确定 K值
-
- 误差平方和(SSE):
- 平均轮廓系数法(Silhouette Coefficient)
- “肘”方法 (Elbow method) — K值确定
- CH系数(Calinski-Harabasz Index)
- 优化算法
-
- 二分 k-means
- k-medoids(k-中心聚类算法)
- Mini-batch K-means
- DBSCAN聚类
-
- DBSCAN 原理
- DBSCAN API
- 异常检测
-
- 孤立森林 Isolation Forest
- 集成学习思想
-
- bagging 和 随机森林
- boosting
-
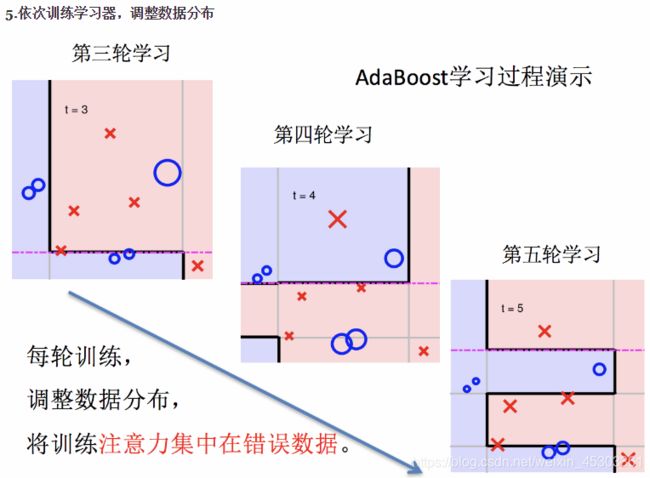
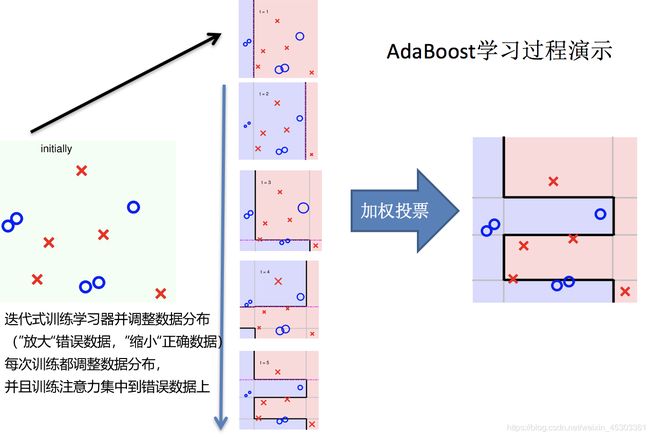
- Adaboost
- GBDT
- XGBoost 和 lightGBM
-
- LightGBM和XGBOOST在原理和性能上的差异?
- bagging集成与boosting集成的区别
- 超参数确定
-
-
- 交叉验证 和 网格搜索
-
回归算法
线型回归(Linear regression)
概念 及 回归方程
概念:利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模
特点:只有一个自变量的情况称为单变量回归,多于一个自变量情况的叫做多元回归
数学公式:
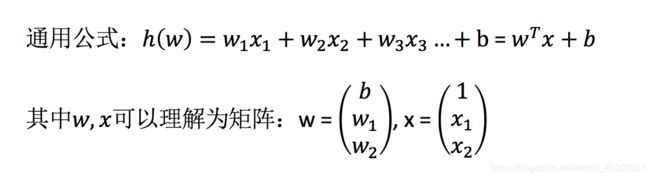

线性回归当中主要有两种模型,一种是线性关系,另一种是非线性关系。
- 线性回归:单特征与目标值的关系呈直线关系,两个特征与目标值呈现平面的关系
- 非线性回归:表现则是曲线或曲面(包含高次项)
损失函数
由于目标值时连续的,无法根据正确率进行判别,而是计算 损失量(预测值和真实值差的平方和) 来判断

损失越小,回归模型越好
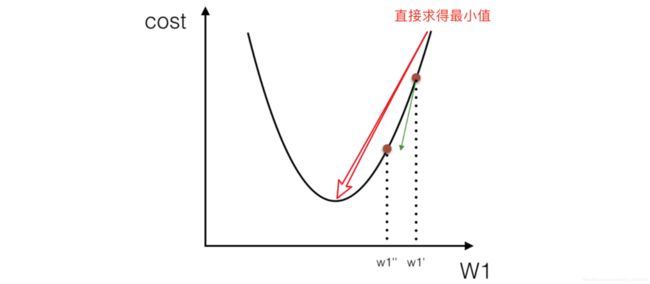
优化算法
通过优化各个自变量的权重(w),使得损失降到最小
常见的优化算法:
- 正规方程 数学方式直接计算(通过微分为零,直接计算出最优权重)
- 梯度下降 通过迭代一步步求解
- 正则化
正规方程 及其 API
X为特征值矩阵,y为目标值矩阵- 接求到最好的结果,但当特征过多过复杂时,求解速度太慢并且可能出现无解情况
对其求解关于w的最小值,起止y,X均已知二次函数直接求导,导数为零的位置,即为最小值。
sklearn API 代码实现
导入模块:from sklearn.linear_model import LinearRegression
正规方程API:LinearRegression(fit_intercept=True)
- 参数
fit_intercept:是否计算偏置normalize:数据是否进行标准化,默认不标准化
可以在特征工程调用preprocessing.StandardScaler标准化数据
- 属性
LinearRegression对象.coef_:回归系数LinearRegression对象.intercept_:偏置
梯度下降 及其 API
梯度:
- 在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
- 在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
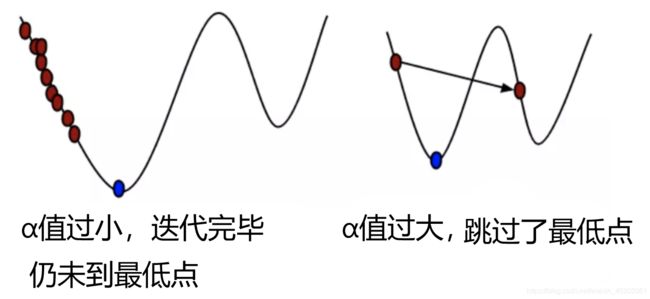
梯度下降:以随机位置为基准,寻找这个位置梯度,往下移动,都反复采用该方法,最后就能成功的抵达(微分为0)最小值位置
常见的梯度下降算法有:
- 全梯度下降算法(
FG)
计算训练集所有样本的最优权重,对其求平均值作为目标函数
优点:可以准确找到最优解
缺点:计算量大,花费时间长,内存消耗大,效率低下 - 随机梯度下降算法(
SG)
仅仅计算训练集中随机的一个样本的最优权重,并作为目标函数
优点:容易陷入局部最优解(慎重选择步长)
缺点:速度快,计算量小 - 随机平均梯度下降算法(
SAG)
在内存中保存每次SG获得的梯度,每次训练结果:新样本与旧样本 所得 所有梯度的平均值,进而更新了参数
缺点:初期表现不佳(因为我们常将初始梯度设为0),优化速度较慢
优点:速度快,计算量小,迭代会越来越精确 - 小批量梯度下降算法(
Mini-batch)
从训练样本集中随机抽取一个小样本集,在抽出来的小样本集上采用FG迭代获取权重
样本点的个数(batch_size),通常设置为2的幂次方,更有利于GPU加速处理
有效的解决了局部最优解的问题,效率也有所提高,为常用的梯度下降算法,是使用最多的梯度下降算法,正是因为它避开了FG运算效率低成本大和SG收敛效果不稳定的缺点
sklearn API 代码实现
SGDRegressor类实现了随机梯度下降学习,它支持不同的loss函数和 正则化拟合线性回归模型
导入模块:from sklearn.linear_model import SGDRegressor
梯度下降API:SGDRegressor(loss="squared_loss", fit_intercept=True,penalty='l2', learning_rate ='optimal', eta0=0.01)
-
参数:
loss:损失函数类型loss="squared_loss":普通最小二乘法
fit_intercept:是否计算偏置penalty='l2':正则化方式。{‘l2’, ‘l1’, ‘elasticnet’}l2岭回归 常用l2Lasso回归 少用elasticnet:弹性网络,综合了岭回归和Lasso回归用于少数特征有效时
normalize:数据是否进行标准化,默认不标准化
可以在特征工程调用preprocessing.StandardScaler标准化数据learning_rate: 学习率(α)填充方式constant: 学习率为常数,并通过eta0=0.01指定optimal:学习率=1.0 / (alpha * (t + t0))默认使用invscaling: 学习率=eta0 / pow(t, power_t)、power_t=0.25:存在父类当中max_iter=1000:int,通过训练数据的最大次数tol = 1e-3:停止训练的精度标准
-
专属属性:
SGDRegressor.coef_:回归系数 (线性回归方程中的权重W)SGDRegressor.intercept_:偏置 (线性回归方程中的常数项b)
正则化(岭回归 及其 API)
概念:算法在学习时尽量减少 影响模型复杂度或者异常点较多 的特征(甚至删除)
-
岭回归(具有
L2正则化的线性回归)
在原来的线性回归的方程 中添加 正则项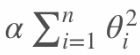 ,使不重要特征 和 高次项特征 的权重 尽可能小:
,使不重要特征 和 高次项特征 的权重 尽可能小:
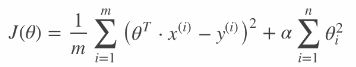
sklearn API代码实现导入模块:
from sklearn.linear_model import Ridge, RidgeCV岭回归API:
Ridge(alpha=1.0, *, fit_intercept=True, normalize=False , solver='auto', random_state=None)
带有交叉验证的岭回归API:RidgeCV(alphas=(0.1, 1.0, 10.0),...)- 参数:
alpha:正则化力度,也叫λ,λ取值:0~1、1~10fit_intercept=True:计算偏置solver:会根据数据自动选择优化方法。{'auto','svd','cholesky','lsqr','sparse_cg','sag','saga'}
sag:如果数据集、特征都比较大,选择该随机梯度下降优化normalize:数据是否进行标准化,默认不标准化
可以在特征工程调用preprocessing.StandardScaler标准化数据max_iter=1000:int,通过训练数据的最大次数tol = 1e-3:停止训练的精度标准
- 专属属性:
Ridge/RidgeCV.coef_:回归系数 (线性回归方程中的权重W)Ridge/RidgeCV.intercept_:偏置 (线性回归方程中的常数项b)Ridge.n_iter_:每个目标的实际迭代次数RidgeCV.alpha_:估计的正则化参数RidgeCV.best_score_:具有最佳alpha值的基本估算器 得分RidgeCV.cv_values_:每个Alpha的交叉验证值(仅当store_cv_values=True和cv=None时可用 )
- 参数:
注:Ridge方法相当于SGDRegressor(penalty='l2', loss="squared_loss"),只不过SGDRegressor实现了一个普通的随机梯度下降学习(SG),而Ridge实现了SAG
-
Lasso回归
在原来的线性回归的方程 中添加L1正则项,将 不重要特征 和 高次项特征 的权重 置为0
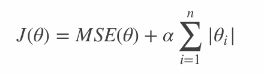
也就是说,Lasso回归能够自动进行特征选择,输出一个稀疏模型(只有少数 特征权重 不是零) -
Elastic Net(弹性网络)
弹性网络在岭回归和Lasso回归中进行了折中,通过 混合比r进行控制:
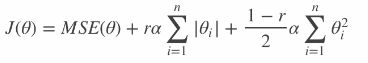
r=0:弹性网络变为岭回归r=1:弹性网络便为Lasso回归
分类算法
K近邻算法
算法简介 及 工作流程
核心为:样本在特征空间中的 k个最相邻样本 中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别的特性。
如图所示:
样本a在特征空间中的5(K值)个最相邻样本中大多数属于类别1,因此我们就认为样本a属于类别1,并具有类别1的特性

算法工作流程
- 选取与当前样本点 最近 的k个样本点
- 统计这k个样本点所在的类别出现的频率
- 返回这k个样本点出现频率最高的类别作为当前点的预测分类
选出最近k个临近样本点的方法:
-
线型扫描(穷举搜索)
计算 所有已知类别样本点 与 当前预测样本点之间的距离,按距离递增次序排序,从而获取k个最邻近样本点
缺点:计算量过大,耗时 -
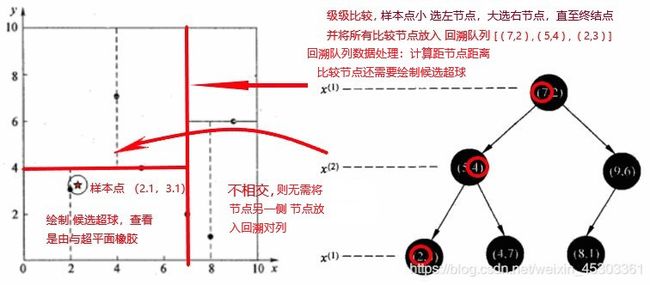
kd 树(类似二叉树的数据结构)
把距离信息保存在一棵树里,这样在计算之前从树里查询距离信息,尽量避免重新计算
一维
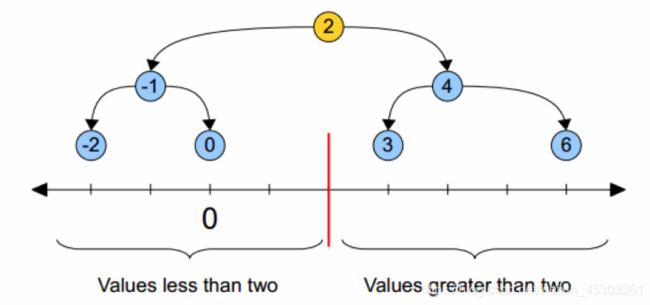
二维
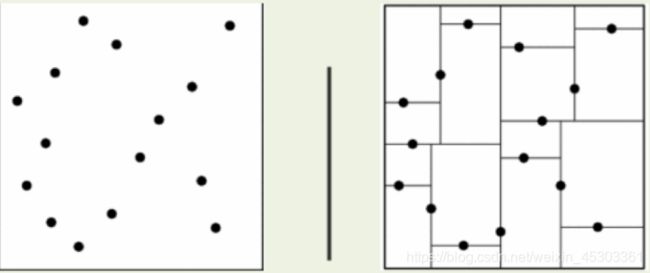
- 构建
kd 树- 选出首次切割维度(选择离散程度大的维度,即 标准差大)
- 选择首次切割点(中位数),将所有数据切为两个超矩形区域
- 垂直于上次切割维度,再次寻找中位数 切割。直至所有样本点均切割
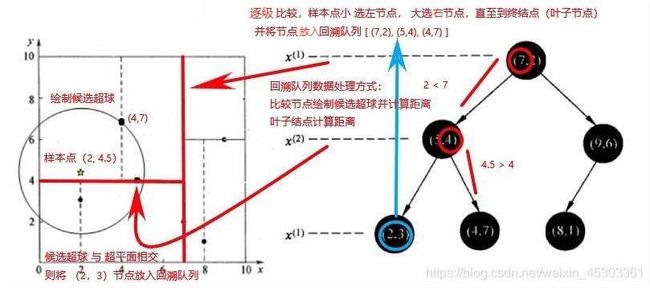
- 最近领域的搜索(候选超球 和 回溯对列)
- 构建
KNN算法 API (sklearn)
导包:from sklearn.neighbors import KNeighborsClassifier
实例化API:estimator = KNeighborsClassifier(n_neighbors=5, weights=’uniform’, algorithm=’auto’, leaf_size=30, **kwargs)
参数:
n_neighbors便是K值,其中的数值是自定义的,但K值的数值直接影响预测结果,K值过小:
容易受到异常点的影响
就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是“学习”的估计误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合k值过大:
受到样本均衡的问题
就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单,容易欠拟合- 在实际应用中,
K值一般取一个比较小的数值,然后采用交叉验证法(简单来说,就是把训练数据在分成两组:训练集和验证集)来选择最优的K值
weights: 预测时使用的权重、可选、默认为uniformuniform:平权,每个邻域中所有点的权重均相等。distance:权重点按其距离的倒数表示。在这种情况下,查询点的近邻比远处的近邻具有更大的影响力。callable:用户定义的函数,它接受距离数组,并返回包含权重的相同形状的数组。
algorithm: 用于计算最近邻居的算法,可选{'auto','ball_tree','kd_tree','brute'}:kd_tree将使用KD-树ball_tree将使用BallTree,对kd- 树高维失效现象进行了优化brute将使用线型扫描暴力搜索,仅限小数据集使用auto将 尝试根据传递给fit方法的值来决定最合适的算法
leaf_size:BallTree或KDTree的叶大小、int型、可选、默认为30
这会影响构造和查询的速度,以及存储树所需的内存。最佳值取决于问题的性质。
优缺点
优点:
- 简单有效
- 重新训练的代价低
- 适合类域交叉样本
KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。 - 适合大样本自动分类
该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
缺点:
-
惰性学习
KNN算法是懒散学习方法(lazy learning,基本上不学习),一些积极学习的算法要快很多 -
类别评分不是规格化
不像一些通过概率评分的分类 -
输出可解释性不强
-
对不均衡的样本不擅长
当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进。 -
计算量较大
目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
朴素贝叶斯
-
使用概率学知识进行计算 类别概率,并将其分到 发生概率最大的类别中
-
在贝叶斯算法的基础上进行了相应的简化(特征 相互独立)
-
有坚实的数学基础,以及稳定的分类效率
-
超参数很少,对缺失数据不太敏感
-
算法也比较简单。理论上,具有最小的误差率
-
特征之间相互独立,在实际应用中往往是不成立的
概率学知识
- 联合概率:包含多个条件,且所有条件同时成立的概率
记作:P(A,B)
特性:P(A,B) =P(A)P(B) - 条件概率:事件A 在 事件B已经发生条件下 的发生概率
记作:P(A|B)
特性: P(A1,A2|B) = P(A1|B)P(A2 1B)
注意:此条件概率的成立,是由于A1,A2相互独立的结果
贝叶斯公式 和 拉普拉斯平滑
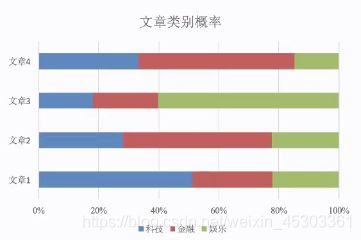
以文章分类去理解别贝叶斯公式:
P(科技|文章) = P(科技|词1, 词2, 词3, 词4, 词5,... ) 一个文章中存在很多词
= P(词1, 词2, 词3, 词4, 词5,... | 科技) P(科技) / P(词1, 词2, 词3, 词4, 词5,... )
P(娱乐|文章) = P(娱乐|词1, 词2, 词3, 词4, 词5,... )
= P(词1, 词2, 词3, 词4, 词5,... | 娱乐) P(娱乐) / P(词1, 词2, 词3, 词4, 词5,... )
因为同一篇文章 且 是 比较概率,所以分母相同 且可以 忽略
P(科技|文章) = P(词1, 词2, 词3, 词4, 词5,... | 科技) P(科技)
P(娱乐|文章) = P(词1, 词2, 词3, 词4, 词5,... | 娱乐) P(娱乐)
其中:
P(词1, 词2, 词3, 词4, 词5,... | 科技) 似然函数
表示:原文章中的词 在 科技类文章中 出现的概率
P(科技) 先验概率。不考虑 文章差异,根据以往经验得到文章属于科技的概率
表示:所有文章 中 科技文章所占的比重

若 原文章中还有 明星 一词,但其 在 科技文章中出现的次数为零
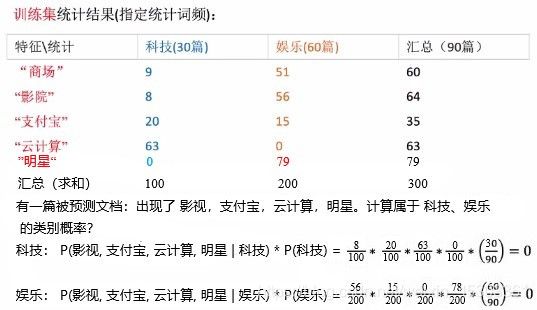
很明显 若原文章中的某词在某类别中没有出现,就视为 其属于该类别的概率为零 是不合理的
朴素贝叶斯API
sklearn
sklearn.naive_bayes.MultinomialNB(alpha=1.0)
参数:
alpha:拉普拉斯平滑系数。float, 默认为1.0
案例:
# 实例化朴素贝叶斯API
mlt = MultinomialNB(alpha=1.0)
# 训练数据
mlt.fit(x_train, y_train)
# 预测
y_predict =mlt.predict(x_test)
# 评估
print ("预测的文章类别为:y_predict) # 得出准确率
print("准确率为: ", mlt.score(x_test, y_test) )
逻辑回归(Logistic Regression)
- 逻辑回归是种分类算法,虽然名字中带有回归
- 该算法的简单和高效,在实际中应用非常广泛
- 逻辑回归是解决二分类问题的利器
应用场景:是否为垃圾邮件、是否患病、是否是虚假账号
逻辑回归方程
输入:逻辑回归的输入就是 一个线性回归的结果
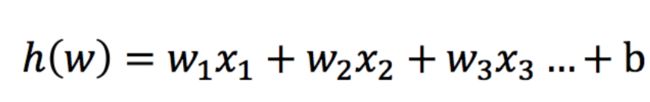
输出:[0,1]之间的概率值
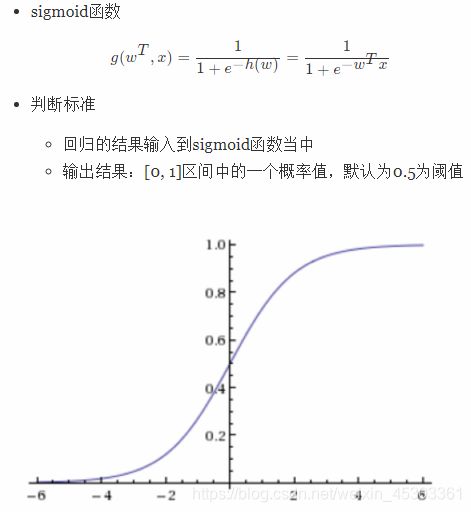
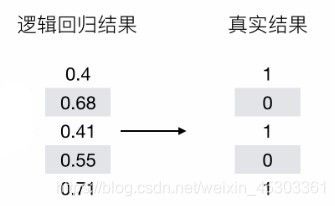
将线性回归的结果作为输出,经过sigmoid函数将其转化为[0,1]之间的数作为概率,若其大于阈值则分为正例,小于阈值则为反例

逻辑回归中阈值是超参数,可以自定义,并且阈值直接影响模型结果,因此需要最佳阈值从而减少损失
损失以及优化
逻辑回归的损失,称之为对数似然损失,公式如下:

合并之后的完整损失函数:
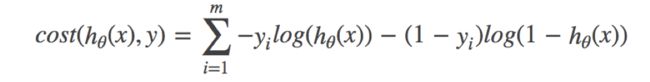
其中:其中y为真实值,hθ(x)为预测值
优化原理:减小损失值(提升原本属于1类别的概率,降低原本是0类别的概率)
优化方法:优化线性回归的方法(梯度下降和正则化),去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数
逻辑回归API
sklearn
API函数:sklearn.linear_model.LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)
-
参数:
solver可选参数:{'liblinear', 'sag', 'saga','newton-cg', 'lbfgs'}- 默认:
liblinear;用于优化问题的算法,适合小数据集,仅限于one-versus-rest分类 sag和saga更适合大型数据集- 对于多分类问题,可选
newton-cg,sag,saga和lbfgs
- 默认:
penalty:正则化的种类,L1表示岭回归、L2为Lasso回归C:正则化力度
-
属性
LogisticRegression.coef_:回归系数 (逻辑回归方程中的权重W)LogisticRegression.intercept_:偏置 (逻辑回归方程中的常数项b),若fit_intercept=False,则截距设置为零LogisticRegression.classes_:分类器已知的类别标签列表LogisticRegression.n_iter_:所有类的实际迭代数y_pred = lr_model.predict_proba(x)[:,1]:获取各样本的概率
默认将类别数量少的当做正例
LogisticRegression方法相当于SGDClassifier(loss="log", penalty=" "),SGDClassifier实现了一个普通的随机梯度下降学习。而使用LogisticRegression(实现了SAG)
Spark ML:训练逻辑回归模型
- 数据的准备 传入DataFrame 一列为目标,一列为特征,需要把所有的特征放到一个特征向量中
- LogisticRegression对象训练模型
- LogisticRegressionModel 预测结果
from pyspark.ml.feature import VectorAssembler
# 根据特征字段计算特征向量
datasets_1 = VectorAssembler().setInputCols(useful_cols[2:]).setOutputCol("features").transform(datasets_1)
# 训练数据集: 约7天的数据
train_datasets_1 = datasets_1.filter(datasets_1.timestamp<=(1494691186-24*60*60))
# 测试数据集:约1天的数据量
test_datasets_1 = datasets_1.filter(datasets_1.timestamp>(1494691186-24*60*60))
from pyspark.ml.classification import LogisticRegression
lr = LogisticRegression()
# 设置目标字段、特征值字段并训练
model = lr.setLabelCol("clk").setFeaturesCol("features").fit(train_datasets_1)
# 对模型进行存储
model.save("hdfs://192.168.19.137:9000/models/CTRModel_Normal.obj")
# 载入训练好的模型
from pyspark.ml.classification import LogisticRegressionModel
model = LogisticRegressionModel.load("hdfs://192.168.19.137:9000/models/CTRModel_Normal.obj")
# 根据测试数据进行预测
result_1 = model.transform(test_datasets_1)
# 按probability升序排列数据,probability表示预测结果的概率
# 如果预测值是0,其概率是0.9248,那么反之可推出1的可能性就是1-0.9248=0.0752,即点击概率约为7.52%
# 因为前面提到广告的点击率一般都比较低,所以预测值通常都是0,因此通常需要反减得出点击的概率
result_1.select("clk", "price", "probability", "prediction").sort("probability").show(100)
result_1.filter(result_1.clk==1).select("clk", "price", "probability", "prediction").sort("probability").show(100)
决策树
决策树:是一个由多个判断节点组成的树形结构
- 每个非叶子节点表示一个属性上的判断(下图中绿色代表非叶子节点)
- 每个分支代表一个判断结果的输出
- 每个叶节点代表一种分类结果(橙色节点代表叶子结点)
决策树分类原理
构造决策树的重点:
- 特征的重要性(非叶子节点 判断条件的先后顺序)
- 特征分割点(非叶子节点开分支的分隔点)
三种构树原理
- 信息增益(
ID3)(熵) - 信息增益率(
C4.5)(熵) CART树(基尼值 和 基尼指数)
熵(Entropy):信息的混乱程度度量,系统信息越有序,熵值越低;越混乱或者分散,熵值越高
基尼值(Gini):随机抽取两个样本,其类别不一致的概率。故基尼值越小,数据集纯度越高
信息增益(ID3)(熵)
信息增益:以某特征划分数据集前后熵的差值,差值越大表示划分所获得的"纯度提升"越大,即该特征更重要,应优先划分
- 仅能处理离散数据(如 性别),无法处理连续型数据(价格)
- 偏好类别多的特征(类别多的特征分类后的熵 会更小)
信息增益率(C4.5)(熵)
增益率:增益率是用前面的信息增益Gain(D, a)和属性a对应的"固有值" 的比值来共同定义
- 解决了信息增益偏好问题,并可以处理连续型数据
- 采用了一种后剪枝方法,避免树的高度无节制的增长,出现过拟合问题
- 能够处理带有缺失值得数据
缺点:
- 需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效
- 只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时程序无法运行
CART 树(基尼值 和 基尼指数)

注意:CART 树 是二叉树,因此多分类问题应转换成(分类1 和 其他 ; 分类2 和 其他 ;…)
计算基尼指数案例:
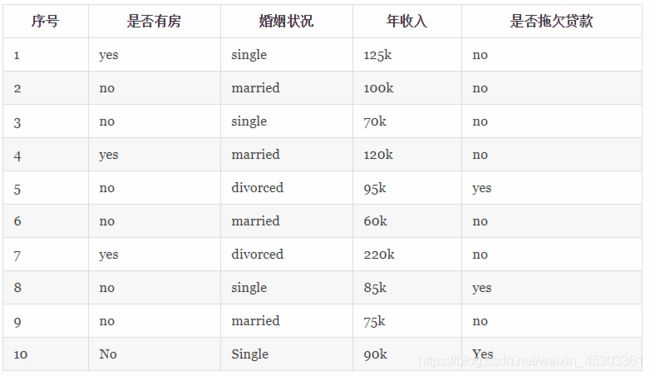
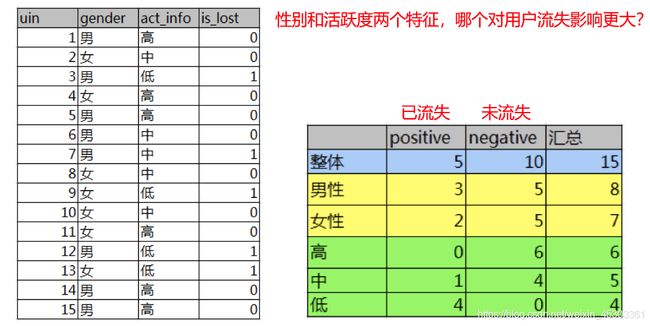
第一个大循环
对数据集非序列标号属性{是否有房,婚姻状况,年收入}分别计算它们的Gini指数,取Gini`指数最小的属性作为决策树的根节点属性
-
若按婚姻状况属性来划分(多分类特征计算基尼值)
属性婚姻状况有三个可能的取值{married,single,divorced},分别计算划分后的Gini系数增益

对比计算结果,根据婚姻状况属性来划分根节点时取 Gini指数 最小的分组作为划分结果,即:{married} | {single,divorced} -
根据 年收入计算
Gini指数(连续数据 计算基尼值 并确定 分隔点)
对于年收入属性为数值型属性,首先需要对数据按升序排序,然后从小到大依次用相邻值的中间值作为分隔将样本划分为两组。例如当面对年收入为60和70这两个值时,我们算得其中间值为65。以中间值65作为分割点求出Gini指数

-
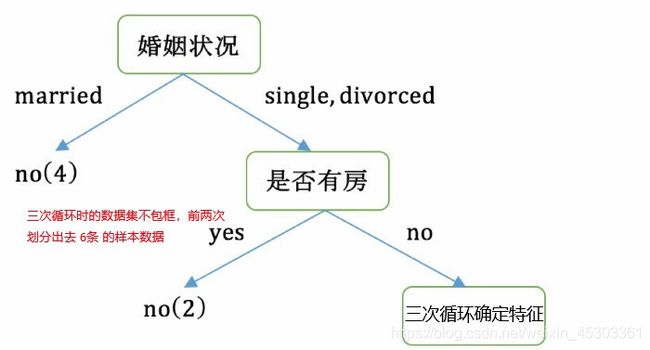
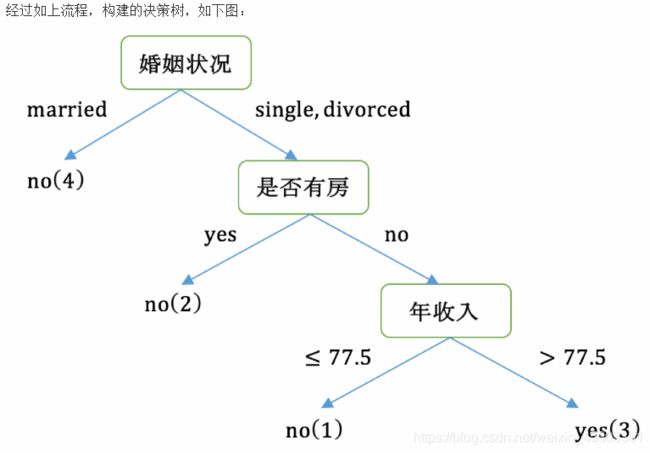
根据计算知道,三个属性划分根节点的指数最小的有两个:年收入属性和婚姻状况,他们的指数都为
0.3。此时,选取首先出现的属性married作为第一次划分

第三次大循环(应去除掉,在前两次循环被分数的数据)
决策树 优化(cart剪枝)
出现这种情况的原因:
- 样本冲突,即错误的样本数据
- 特征即属性不能完全作为分类标准
- 巧合的规律性,数据量不够大。
改进:
- 减枝cart算法
- 预剪枝(构树前设定好限制条件,当达到限制条件,树将不再延伸)
- 限制节点最小样本数
- 指定数据高度
- 指定熵值的最小值
- 后剪枝(构建完成之后,再进行从下往上的剪枝)
- 对比修剪前后的效果,若变好,则将减掉
- 预剪枝(构树前设定好限制条件,当达到限制条件,树将不再延伸)
- 随机森林(集成学习
bagging+ 决策树)
决策树 API 及 可视化
sklearn
决策数 API:sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
criterion特征选择标准
基尼指数gini或者 熵entropy,默认gini,即CART算法min_samples_split:预剪枝时,内部节点再划分所需最小样本数
这个值限制了子树继续划分的条件,如果某节点的样本数少于min_samples_split,则不会继续再尝试选择最优特征来进行划分。 默认是2。参考:10万样本,min_samples_split=10。min_samples_leaf:预剪枝时,叶子节点最少样本数
这个值限制了叶子节点最少的样本数,如果某叶子节点数目小于样本数,则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数,或者最少样本数占样本总数的百分比。参考:10万样本项目使用min_samples_leaf的值为5max_depth:预剪枝时,决策树最大深度
决策树的最大深度,默认可以不输入,如果不输入的话,决策树在建立子树的时候不会限制子树的深度。常用的可以取值10-100之间random_state随机数种子
决策树可视化 API:sklearn.tree.export_graphviz(决策树模型,out_file='保存路径/文件名.dot’) 该函数能够导出DOT格式
参数:
feature_names=[‘’特征列表’’]:每个特征的名字,便于观看。feature_names=分类器.get_feature_namesfilled:指定是否为节点上色max_depth: 指定展示出来的树的深度,可以用来控制图像大小
查看dot文件,需要使用Graphviz这个工具,一种是执行pip install graphviz,然后可以在pyhton调用,另一种是使用命令行,这里我们采用第二种,但是是在python里调用的外部命令行
# 临时将Graphviz添加到环境变量中
import os
os.environ["PATH"]+= os.pathsep + 'C:/Program Files (x86)/Graphviz2.38/bin/'
# 将tree.dot文件转化为tree.png
with open("tree.dot", "w") as f:
tree.export_graphviz(dtree, out_file=f)
dot_data = StringIO()
tree.export_graphviz(dtree, out_file=dot_data,
feature_names=x.columns,
class_names=['bad_ind'],
filled=True, rounded=True,
special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())
聚类算法
一种无监督学习算法,主要用于将相似的样本自动归到一个类别中。
在聚类算法中根据样本之间的相似性,将样本划分到不同的类别中,不同的相似度计算方法(聚类准则),会得到不同的聚类结果,常用的相似度计算方法有欧式距离法

K-means
k-means 聚类原理
k-means聚类其实包含两层内容:
-
K值: 初始中心点个数(计划聚类数) means:求中心点到其他数据点距离的平均值
k-means聚类步骤:
- 事先确定常数
K,常数K意味着最终的聚类的 类别数 - 随机设置
K个特征空间内的点作为 初始的聚类中心(质心) - 对于其他每个点计算到K个中心的距离(欧氏距离),并选择最近的一个聚类中心点作为标记类别
- 标记完所有样本点之后,重新计算出每个聚类的新中心点(平均值)
- 如果计算得出的新中心点与原中心点一样(质心不再移动),那么结束,否则重新进行第二步过程

K-Means停止迭代条件
- 设定迭代次数
- 设定当前中心点与上一个中心点的差值小于阈值 停止迭代
注意:由于每次都要计算所有的样本与每一个质心之间的距离,故在大规模的数据集上,K-Means算法的收敛速度比较慢
K-means API
sklearn.cluster.KMeans(n_clusters = 8,*,init ='k-means ++',n_init = 10,max_iter = 300,tol = 0.0001,random_state = None,algorithm ='auto' )
参数:
n_clusters:聚类中心数量,int型,默认为8,生成的聚类数,即产生的质心数init:初始质心的位置{‘k-means++’, ‘random’, ndarray, callable},默认为’k-means++’k-means++:让选择的质心尽可能的分散,防止陷入局部最优解random:随机,可能陷入局部最优解ndarray,则其形状应为(n_clusters,n_features),给定初始中心callable:则应使用参数X,n_clusters和 随机状态并返回初始化
n_init: k均值算法将在不同质心种子下运行的次数,默认值为10max_iter: 单次运行的k均值算法的最大迭代次数,默认为300tol: 迭代停止条件,默认为1e-4random_state随机数种子
属性:
cluster_centers_:ndarray of shape (n_clusters, n_features)
集群中心的坐标。如果算法在完全收敛之前停止(tol和max_iter),则这些将与labels_不一致labels_:ndarray of shape (n_samples,)
每个点的标签inertia_:float
样本到其最近的聚类中心的平方距离的总和n_iter_:int
运行的迭代次数
方法:
estimator.fit(x)计算聚类中心estimator.predict(x)预测estimator.fit_predict(x)计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)estimator.get_params([deep]):获取此估计量的参数
注意:K-Means算法对异常值和异常纲量比较敏感,因此需要去除异常值和标准化
评估模型 并 确定 K值
误差平方和(SSE):
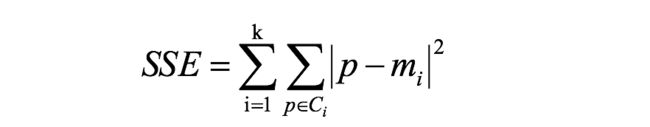
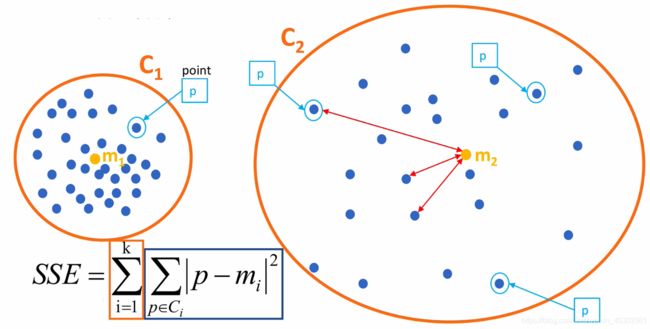
SSE图最终的结果,对图松散度的衡量.(eg: SSE(左图)<SSE(右图))
SSE随着聚类迭代,其值会越来越小,直到最后趋于稳定:
但是如果质心的初始值选择欠佳,SSE可能会达到局部最优解
平均轮廓系数法(Silhouette Coefficient)
结合了聚类的凝聚度(Cohesion)和分离度(Separation),用于评估聚类的效果:

a:组内距离 越小越好
b:组之间距离 越大越好
S:(-1,1)之间 越接近1 越好;越接近-1 效果差
每次聚类后,每个样本都会得到一个轮廓系数
- 当它为1时,说明这个点与周围簇距离较远,结果非常好
- 当它为0时,说明这个点可能处在两个簇的边界上
- 当值为负时,暗含该点可能被误分了
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数([-1,1],系数越大,聚类效果越好)
sklearn API:
sklearn.metrics.silhouette_score(X, labels, *, metric='euclidean', sample_size=None, random_state=None, **kwds)
参数:
X:样本之间的成对距离数组 或 特征值数组
labels:被聚类标记的目标值(预测后的数据集)
sample_size:子集样本大小(随机抽取一部分计算轮廓系数)默认使用所有数据
“肘”方法 (Elbow method) — K值确定
- 对于n个点的数据集,迭代计算k from 1 to n,每次聚类完成后计算每个点到其所属的簇中心的距离的平方和;
- 平方和是会逐渐变小的,直到k==n时平方和为0,因为每个点都是它所在的簇中心本身。
- 在这个平方和变化过程中,会出现一个拐点也即“肘”点,下降率突然变缓时即认为是最佳的k值。
在决定什么时候停止训练时,肘形判据同样有效,数据通常有更多的噪音,在增加分类无法带来更多回报时,我们停止增加类别。
import matplotlib.pyplot as plt
wcss =[]
for i in range (1, 11): # 循环使用不同k测试结果
kmeans =KMeans (n_clusters =i, init ='k-meanst++', random_state = 42)
kmeans.fit_predict(X)
wcss.append(kmeans.inertia_) # inertia 簇内误差平方和
plt.plot(range(1, 11), wcss)
plt.show()
CH系数(Calinski-Harabasz Index)
类别内部数据的协方差越小越好,类别之间的协方差越大越好(即:类别内部数据的距离平方和越小越好,类别之间的距离平方和越大越好),
这样的Calinski-Harabasz分数s会高,分数s高则聚类效果越好

CH需要达到的目的: 用尽量少的类别聚类尽量多的样本,同时获得较好的聚类效果
模型的 CH指数 也大越好
sklearn API
from sklearn.metrics import calinski_harabaz_score # 导包
y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(X) # 使用 K-means 对数据集X进行聚类
calinski_harabaz_score(X, y_pred) # 获取 CH 指数;y_pred
优化算法
k-means优缺点
- 优点:
- 原理简单(靠近中心点),实现容易
- 聚类效果中上(依赖K的选择)
- 空间复杂度o(N),时间复杂度o(IKN)
N为样本点个数,K为中心点个数,I为迭代次数
- 缺点:
- 对离群点,噪声敏感 (中心点易偏移)
- 很难发现大小差别很大的簇及进行增量计算
- 结果不一定是全局最优,只能保证局部最优(与K的个数及初值选取有关)
二分 k-means
- 所有点作为一个簇
- 将该簇一分为二
- 选择能最大限度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇。
- 以此进行下去,直到簇的数目等于用户给定的数目k为止
k-medoids(k-中心聚类算法)
K-medoids和K-means最大的区别是中心点的选取方式
K-means中,根据当前簇所有数据点的平均值确定中心点,小数据集对异常点很敏感K-medoids中,根据点与当前簇其他所有点的距离之和最小确定中心点
算法流程:
- 总体
n个样本点中任意选取k个点作为medoids - 按照与
medoids最近的原则,将剩余的n-k个点分配到当前最佳的medoids代表的类中 - 对于第
i个类中除对应medoids点外的所有其他点,按顺序计算当其为新的medoids时,代价函数的值,遍历所有可能,选取代价函数最小时对应的点作为新的medoids - 重复
2-3的过程,直到所有的medoids点不再发生变化或已达到设定的最大迭代次数 - 产出最终确定的k个类
Mini-batch K-means
适合大数据的聚类算法
样本量大于1万时,就需要考虑选用Mini Batch K-Means算法
使用了Mini Batch(分批处理)的方法对数据点之间的距离进行计算
Mini Batch计算过程中不必使用所有的数据样本,而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。由于计算样本量少,所以会相应的减少运行时间,但另一方面抽样也必然会带来准确度的下降。
该算法的迭代步骤:
- 从数据集中随机抽取一小部分样本 计算质心
- 再抽取一部分 计算质心,求两次质心的均值,作为质心
- 不断迭代,直到质心稳定,或者达到指定的迭代次数 停止计算
与Kmeans相比,数据的更新在每一个小的样本集上。对于每一个小批量,通过计算平均值得到更新质心,并把小批量里的数据分配给该质心,随着迭代次数的增加,这些质心的变化是逐渐减小的,直到质心稳定或者达到指定的迭代次数,停止计算
sklearn.cluster.MiniBatchKMeans(n_clusters = 8,*,init ='k-means ++',max_iter = 100,batch_size = 100,
random_state = None,tol = 0.0,max_no_improvement = 10,init_size = None,n_init = 3)
参数:
n_clusters:聚类中心数量,int型,默认为8,生成的聚类数,即产生的质心数
init:初始质心的位置 {‘k-means++’, ‘random’, ndarray, callable} ,默认为’k-means++’
k-means++:让选择的质心尽可能的分散,防止陷入局部最优解
random:随机,可能陷入局部最优解
ndarray:则其形状应为(n_clusters,n_features),给定初始中心
callable:则应使用参数 X , n_clusters 和 随机状态并返回初始化
n_init : k均值算法将在不同质心种子下运行的次数,默认值为10
max_iter : 单次运行的k均值算法的最大迭代次数,默认为300
batch_size: Mini 批次的大小,默认为100
compute_labels: 一旦小批量优化收敛到合适状态,就可以为整个数据集计算 标签 和inertia,默认为True
max_no_improvement: 基于连续的小批量数量来控制提前停止,默认为10
tol : 迭代停止条件,默认为 1e-4
random_state :随机数种子
reassignment_ratio: float,默认= 0.01
控制重新分配的中心的最大计数数量的分数。值越大越容易重新分配计数较低的中心,
模型将花费更长的时间进行收敛,但是收敛效果更好。
属性:
cluster_centers_:ndarray of shape (n_clusters, n_features)
集群中心的坐标。如果算法在完全收敛之前停止( tol 和 max_iter ),则这些将与 labels_ 不一致
labels_ :ndarray of shape (n_samples,) 。每个点的标签
inertia_ :float 。样本到其最近的聚类中心的平方距离的总和
| 优化方法 | 思路 | 作用 |
|---|---|---|
Canopy+k-means |
Canopy粗聚类配合k-means |
找到最优初始中⼼,减少噪点干扰 |
kmeans++ |
选择的质心尽可能的分散 | 避免陷入局部最优解 |
二分k-means |
拆除SSE最大的簇 | 使数据点更接近于其质心,提高聚类效果 |
k-medoids |
根据点的距离之和最小确定中心点 | 提高噪声鲁棒性,用于小数据集 |
kernel kmeans |
映射到高维空间然后k-means处理 |
- |
ISODATA |
动态聚类,可以更改K值大小 | - |
Mini-batch K-Means |
大数据集分批聚类 | - |
DBSCAN聚类
- 具有噪声的基于密度的聚类方法
- 该算法将具有足够密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的簇,它将簇定义为密度相连的点的最大集合
DBSCAN 的 几个定义:
- Ε邻域:样本点为圆心 给定半径(Ε:超参数)圆内的区域 称为 该样本点的Ε邻域;
- 核心对象:如果给定样本点Ε邻域内的样本点数大于等于
MinPts(超参数),则称该对象为核心对象; - 直接密度可达:对于样本集合D,如果样本点q 在 p的Ε邻域内,并且p为核心对象,那么对象q从对象p直接密度可达。
- 密度可达:对于样本集合D,给定一串样本点p1,p2….pn,若样本点pi 与 pi-1 直接密度可达,那么样本点p1 与 密度可达。
- 密度相连:存在样本集合D中的一点o,如果对象o到对象p和对象q都是密度可达的,那么p和q密度相联
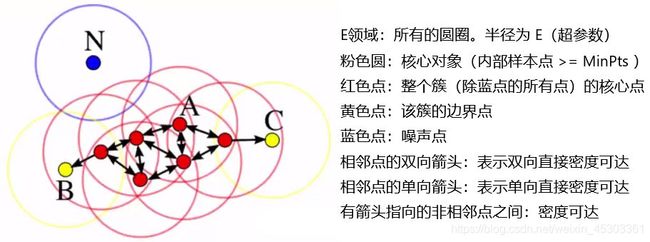
DBSCAN 原理
- 输入: 包含
n个样本的数据集,E领域半径e,形成核心对象的最少样本数MinPts - 输入的
n个样本皆为 未标记数据 - 从中随机选择一个未标记样本点,绘制
E领域- 若是 核心点(可以形成 核心对象),找出所有从该点密度可达的样本点,形成一个簇
- 若是 边缘点 或 噪点 ,则 跳出本次循环,随机选择下个未标记样本点 进行循环;直至所有点都被标记
- 输出:所有生成的簇(达到密度要求)
注意:DBSCAN对超参数(e、MinPts)很敏感,细微的不同都可能导致差别很大的结果,并且参数的选择无规律可循,只能靠经验确定
超参数确定
E领域 半径e
寻找一个样本,计算其与其他样本点的距离,排序后 寻找 距离突变点 作为 半径- 形成核心对象的最少样本数
MinPts
该参数相当于是一个密度,一般这个值都是偏小一些,然后进行多次尝试
DBSCAN API
sklearn API:
sklearn.cluster.DBSCAN(eps=0.5, *, min_samples=5, metric='euclidean', algorithm='auto', leaf_size=30, n_jobs=None)
参数:
eps:E领域的半径;float, default=0.5
min_samples:形成核心领域的最少样本数(包括本身点);int, default=5
metric:计算距离的方法;string, or callable, 默认为’euclidean’(欧氏距离)
若是 string or callable,则它必须是 sklearn.metrics.pairwise_distancesmetric 参数允许的选项之一
若是“precomputed”,则X被视为距离矩阵,并且必须为方阵。若X是词汇表,则只有“非零”元素可以被视为DBSCAN的邻居
algorithm:查找最近的邻居的方法;{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’
kd_tree :建立 kd树(候选超球 和 回溯对列)(具体查看KNN算法的工作流程)
ball_tree :将使用 BallTree ,对 kd- 树 高维失效现象进行了优化
brute : 将使用线型扫描**暴力搜索**,仅限小数据集使用
auto:将 尝试根据传递给 fit 方法的值 来决定最合适的算法
leaf_size:叶大小;int, default=30
传递给BallTree或cKDTree。会影响构造和查询的速度,以及存储树所需的内存。最佳值取决于问题的性质
n_jobs:并行运行的作业数;int, default=None
None除非joblib.parallel_backend上下文中,否则表示1 。 -1表示使用所有处理器
属性:
core_sample_indices_:核心对象指标;ndarray of shape (n_core_samples,)
components_:核心样本的副本;ndarray of shape (n_core_samples, n_features)
labels_:聚类标签;ndarray of shape (n_samples)
赋予fit()的数据集中每个点的聚类标签。噪声样本的标签为-1
异常检测
- 异常点的出现有多种原因
- 业务操作的影响(典型案例:网站广告费用增加10倍,导致流量激增)
- 数据采集问题(典型案例:数据缺失、不全、溢出、格式匹配等问题)
- 数据同步问题(异构数据库同步过程中的丢失、连接错误等导致的数据异常)
- 在对离群点进行挖掘分析之前,需要从中区分出真正的“离群数据”,将“垃圾数据”去掉。
- 异常值检测常用于异常订单识别、风险客户预警、黄牛识别、贷款风险识别、欺诈检测、技术入侵等
- 异常检测的结果只能用来缩小排查范围、为业务的执行提供更加精准和高效的执行目标而已
孤立森林 Isolation Forest
-
一种适用于连续数据的无监督异常检测方法
-
从高维不详解业务的数据中找到异常数据
-
对特征的要求低,不需要去空、离散化、标准化,不需要做特征过滤和筛选
-
孤立森林的原理:
-
iTree孤立树的建立- 从N条数据中均匀抽样(一般是无放回抽样)出ψ个样本出来,作为这颗树的训练样本
- 在样本中,随机选一个特征,并在这个特征的所有值范围内(最小值与最大值之间)随机选一个值,对样本进行二叉划分
- 将样本中小于该值的划分到节点的左边,大于等于该值的划分到节点的右边,由此得到一个分裂条件和左、右两边的数据集
- 然后分别在左右两边的数据集上重复上面的过程,直到数据集只有一条记录或者达到了树的限定高度
from sklearn.ensemble import IsolationForest
model_isof = IsolationForest(n_estimators=20, n_jobs=1) # n_estimators树个数,
outlier_label = model_isof.fit_predict(数据集)
结果:异常数据标为-1,正常数据标为1
集成学习思想
工作原理:生成多个分类器/模型,各自独立地学习和作出预测,然后通过组合或投票 得出最终预测,因此优于任何一个单分类的做出预测
注意:集成学习并不是一种算法,而是一种可以配合多种算法使用的思想
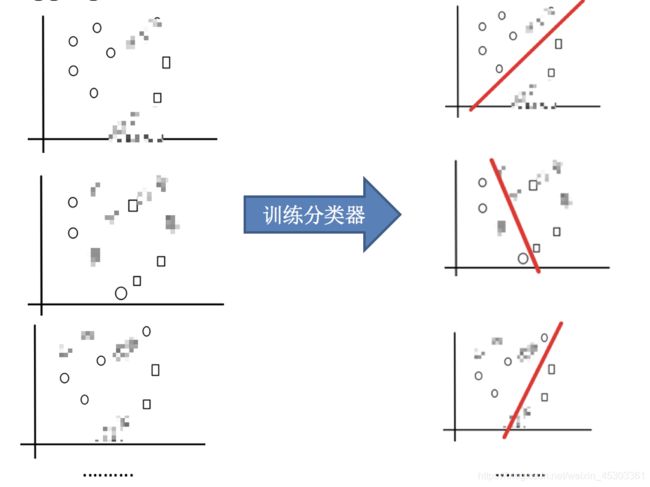
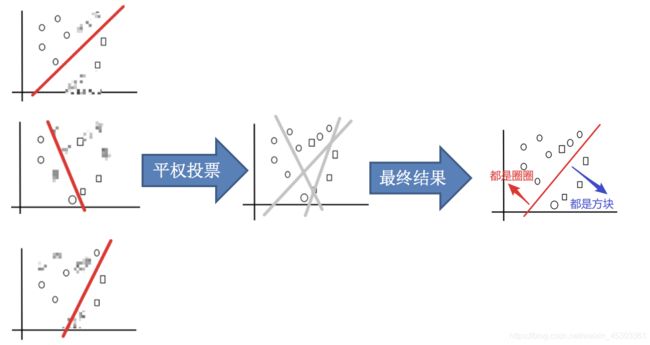
bagging 和 随机森林
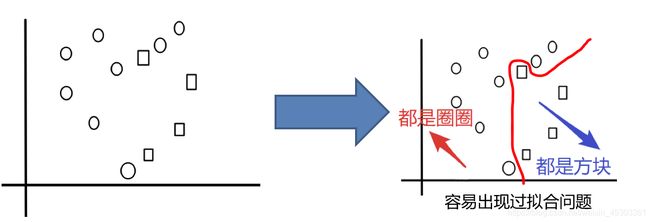
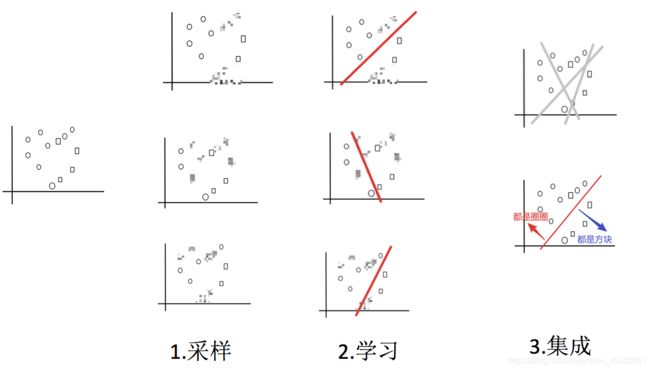
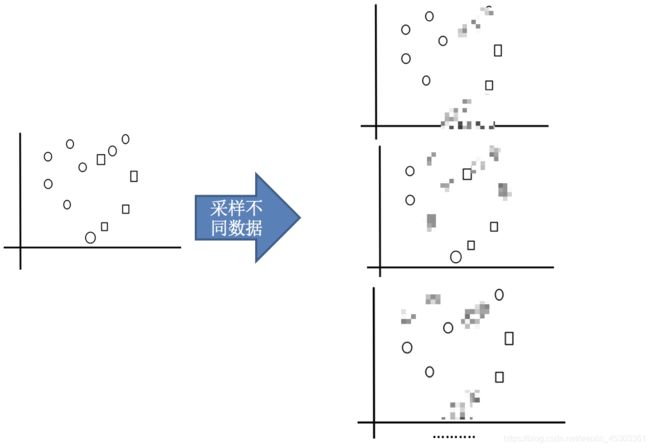
目标:把下面的圈和方块进行分类
bagging集成优点
Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法
经过上面方式组成的集成学习方法:
- 均可在原有算法上提高约2%左右的泛化正确率
- 简单, 方便, 通用
sklearn
bagging 分类器 API:
sklearn.ensemble.BaggingClassifier(base_estimator=None, n_estimators=10, *, max_samples=1.0, max_features=1.0,
bootstrap=True, oob_score=False, warm_start=False, n_jobs=None, random_state=None, verbose=0)
参数:
base_estimator:基于那种模型做集成学习,默认为决策树
n_estimators:训练的小模型数量,默认= 10
max_samples:随机抽取的最大样本数
如果为int,则抽取max_samples个样本
如果为float,则抽取样品数:max_samples * X.shape[0]
max_features:随机抽取的最大特征数
如果为int,则抽取的max_features个特征
如果为float,抽取最大特征数:max_features * X.shape[1]
bootstrap:是否又放回抽取,默认为 True
oob_score:是否使用现成的样本来估计泛化误差
n_jobs:并行运行的作业数
random_state:随机数种子
随机森林API:bagging + 决策树
sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True,
random_state=None, min_samples_split=2)
参数:
n_estimators:integer,可选(默认为10)森林里的树木数量120,200,300,500,800,1200
Criterion:{“gini”, “entropy”},默认为“gini” 建 CART 树。“entropy”表示建立 C4.5 决策树
max_depth:integer或None,可选(默认=无)树的最大深度 5,8,15,25,30
max_features="auto”,每个决策树的最大特征数量
如果 = "auto、sqrt、None", 则max_features=sqrt(n_features) 开根号
如果 = "log2", 则 max_features=log2(n_features)
如果为 int,则max_features在每个拆分处考虑要素
如果为float,则每次拆分时考虑特征个数为:int(max_features * n_features)
bootstrap:boolean,可选(default = True)是否在构建树时使用放回抽样
min_samples_split:节点划分最少样本数
min_samples_leaf:叶子节点的最小样本
n_jobs:int,(默认=无) 要并行运行的作业数
random_state:随机数种子
超参数:n_estimator, max_depth, min_samples_split,min_samples_leaf
属性:
base_estimator_ :最优模型
estimators_ :决策树列表
classes_ :类标签(单个输出问题)或类标签数组列表(多输出问题)
n_classes_ :类数(单个输出问题),或包含每个输出的类数的列表(多输出问题)
超参数可用网格搜索筛选最优参数
# 实例化随机森林API
rf = RandomForestClassifier()
# 定义超参数的选择列表
param = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}
# 使用GridSearchCV进行网格搜索 进行 超参数调优
gc = GridSearchCV(rf, param_grid=param, cv=2)
# 训练模型
gc.fit(x_train, y_train)
# 模型评估
print("随机森林预测的准确率为:", gc.score(x_test, y_test))
spark
from pyspark.mllib.regression import LabeledPoint
# Labeled point 标记点是与标签/响应相关联的密集或稀疏的局部矢量
# 在MLlib中,标记点用于监督学习算法。我们使用double来存储标签,因此我们可以在回归和分类中使用标记点
# 对于二分类情况,目标值应为0(负)或1(正)。对于多分类,标签应该是从零开始的类索引:0, 1, 2, …。 标记点表示为 LabeledPoint。
# 选出new_user_class_level全部的
data2 = data1.rdd.map(
lambda r:LabeledPoint(r.class_level - 1, [r.cms_segid, r.cms_group_id, 特征3 ...]))
# 将标签列class_level 变成从零开始
from pyspark.mllib.tree import RandomForest
model2 = RandomForest.trainClassifier(data2, 4, {}, 10) # 训练集数据 四个分类 不标明目标列 10颗树
model2.predict()
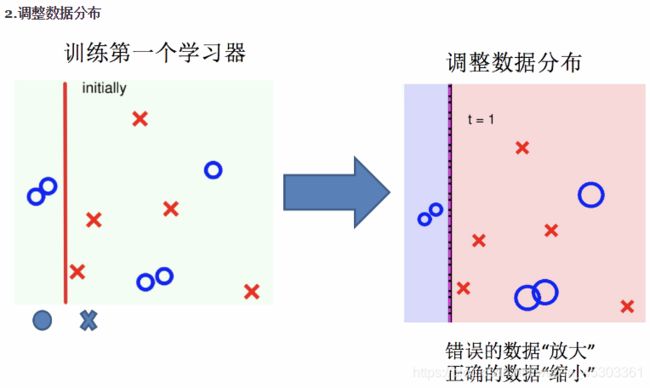
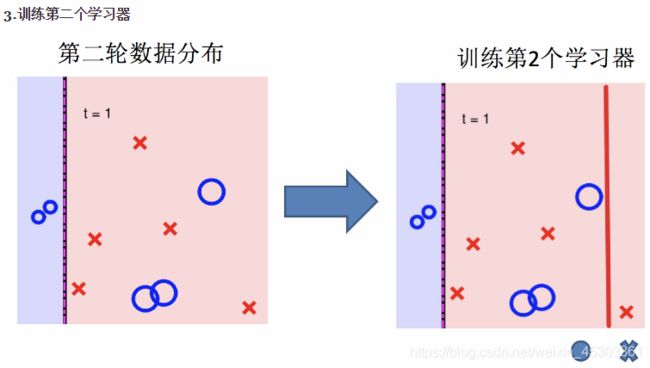
boosting
集成原理:随着学习的积累从弱到强,分段拟合
简而言之:每新加入一个弱学习器,整体能力就会得到提升
代表算法:Adaboost,GBDT,XGBoost
Adaboost
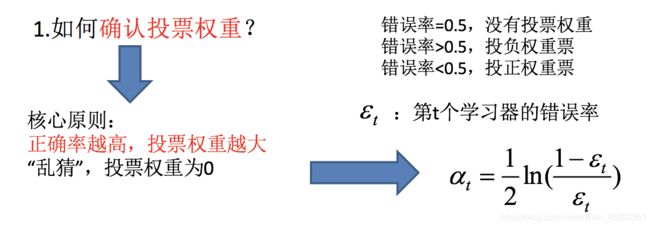
sklearn
sklearn.ensemble.AdaBoostClassifier(base_estimator=None, *, n_estimators=50, learning_rate=1.0,
algorithm='SAMME.R', random_state=None)
参数:
base_estimator : 对象,可选。用于构建增强后的基本模型,默认基本估计量为决策树
n_estimators : int,可选(默认值为50)终止增强的估计器的最大数量。在完美配合的情况下,学习程序会尽早停止
learning_rate : float,可选(默认为1.)学习率缩小了每个分类器的贡献 learning_rate。
random_state : 随机数种子
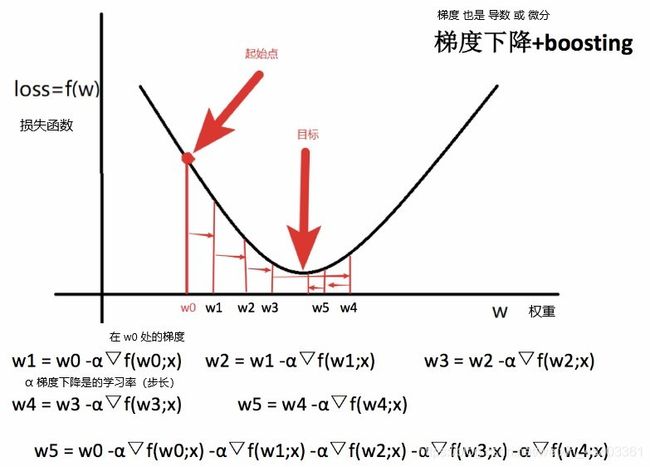
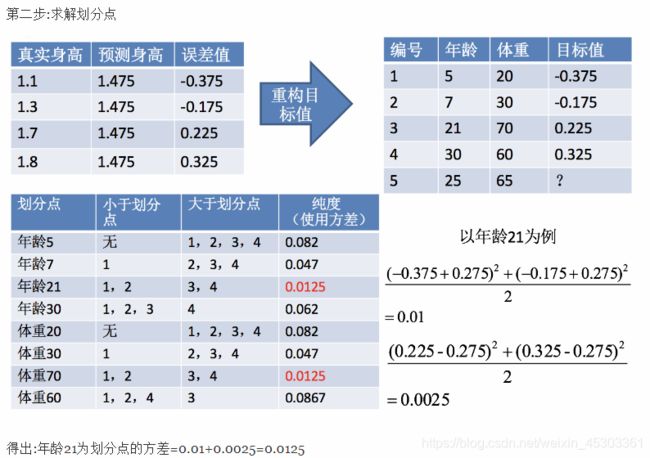
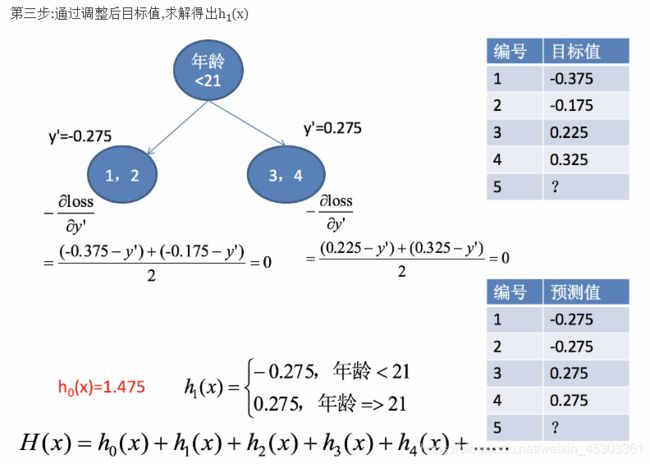
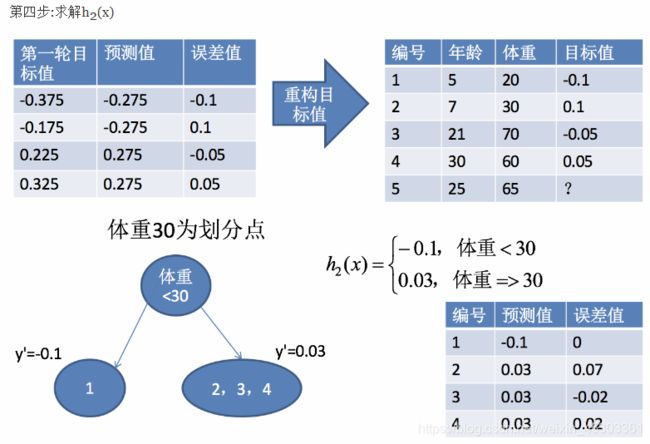
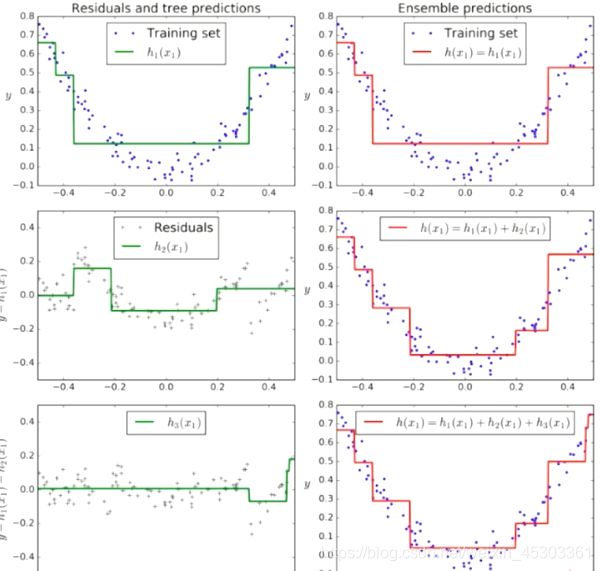
GBDT
梯度提升决策树(GBDT Gradient Boosting Decision Tree):一种迭代的决策树算法,该算法由多棵决策树组成,所有树的结论累加起来做最终答案。具有较强的泛化能力,多用于搜索排序的机器学习模型而
GBDT = 梯度下降 + Boosting + 决策树
- 使用梯度下降法优化代价函数;
- 使用一层决策树作为弱学习器,负梯度作为目标值;
- 利用
boosting思想进行集成
sklearn
sklearn.ensemble.GradientBoostingClassifier(*,learning_rate = 0.1,n_estimators = 100,subsample = 1.0,min_samples_split = 2,min_samples_leaf = 1,max_depth = 3,init = None,random_state = None,tol = 0.0001,ccp_alpha = 0.0 )
参数:
learning_rate:梯度下降的学习率,也时每个弱学习器的权重缩减系数 float,默认= 0.1
n_estimators:也就是弱学习器的最大迭代次数,或者说最大的弱学习器的个数 int,默认= 100
subsample:采样比例,默认= 1.0,即全采样;如果小于1.0,会导致方差减少和偏差增加。推荐在[0.5, 0.8]之间
max_depth:integer或None,可选(默认=无)树的最大深度 5,8,15,25,30
max_features="auto”,每个决策树的最大特征数量
如果 = "auto、sqrt、None", 则max_features=sqrt(n_features) 开根号
如果 = "log2", 则 max_features=log2(n_features)
如果为 int,则max_features在每个拆分处考虑要素
如果为float,则每次拆分时考虑特征个数为:int(max_features * n_features)
min_samples_split:节点划分最少样本数
min_samples_leaf:叶子节点的最小样本
tol:迭代提前终止条件 float,默认= 1e-4
当损失至少不能改善n_iter_no_change迭代次数(如果设置为数字)时,训练将停止
random_state:随机数种子
XGBoost 和 lightGBM
XGBoost/lightGBM= 二阶泰勒展开+boosting+决策树+正则化
Boosting:XGBoost使用Boosting提升思想对多个弱学习器进行迭代式学习- 二阶泰勒展开:每一轮学习中,
XGBoost对损失函数进行二阶泰勒展开,使用一阶和二阶梯度进行优化。 - 决策树:在每一轮学习中,
XGBoost使用决策树算法作为弱学习进行优化。 - 正则化:在优化过程中
XGBoost为防止过拟合,在损失函数中加入惩罚项,限制决策树的叶子节点个数以及决策树叶子节点的值。
原理:每一棵树学的是之前所有回归树 结论和 的 残差
import xgboost as xgb
from sklearn.externals import joblib
# 初始化模型
xgb_classifier = xgb.XGBClassifier(n_estimators=20,\
max_depth=4, \
learning_rate=0.1, \
subsample=0.7, \
colsample_bytree=0.7)
# 拟合模型
xgb_classifier.fit(train_X, train_y)
# 使用模型预测
preds = xgb_classifier.predict(test_X)
# 判断准确率
print ('错误类为%f' %((preds!=test_y).sum()/float(test_y.shape[0])))
# 模型存储
joblib.dump(xgb_classifier, '2.model')
参数:
booster [default=gbtree]:gbtree和gblinearsilent [default=0]:0表示输出信息, 1表示安静模式nthread:跑xgboost的线程数,默认最大线程数eta [default=0.3]:学习率(新模型的权重占比),取值范围为:[0,1]gamma [default=0, alias: min_split_loss]:叶子节点进一步的分割的最小损失值,该值越大,算法越保守max_depth [default=6]:树的最大深度min_child_weight [default=1]:子树权重之和的最小值,如果树的生长时的某一步所生成的叶子结点,其权重之和小于min_child_weight,那么可以放弃该步生长,。该值越大,算法越保守subsample [default=1]:子样本的占比,范围(0,1]colsample_bytree [default=1]:构造每棵树时 选取的特征占比,范围 (0,1]lambda [default=1, alias: reg_lambda]:L2 权重的L2正则化项alpha [default=0, alias: reg_alpha]: L1 权重的L1正则化项scale_pos_weight, [default=1]:样本不均衡时,把这个参数设定为一个正值,可以使算法更快收敛objective [ default=reg:linear ]:定义需要被最小化的损失函数reg:linear--线性回归reg:logistic--逻辑回归binary:logistic--二分类的逻辑回归,返回预测的概率(不是类别)binary:logitraw--输出归一化前的得分
seed [ default=0 ]:随机种子
LightGBM和XGBOOST在原理和性能上的差异?
- 速度和内存上的优化:
xgboost用的是预排序 的方法, 空间消耗大
这样的算法需要保存数据的特征值,还保存了特征排序的结果(例如排序后的索引,为了后续快速的计算分割点),这里需要消耗训练数据两倍的内存。
其次,时间上也有较大的开销,在遍历每一个分割点的时候,都需要进行分裂增益的计算,消耗的代价大。LightGBM用的是直方图 的决策树算法,直方图算法的基本思想是先把连续的浮点特征值离散化成k个整数,同时构造一个宽度为k的直方图。在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。
- 准确率上的优化:
xgboost通过level(depth)-wise策略生长树,Level-wise过一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。LightGBM通过leaf-wise(best-first)策略来生长树,Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
- 对类别型特征的处理:
xgboost不支持直接导入类别型变量,需要预先对类别型变量作亚编码等处理。如果类别型特征较多,会导致哑变量处理后衍生后的特征过多,学习树会生长的非常不平衡,并且需要非常深的深度才能来达到较好的准确率。LightGBM可以支持直接导入类别型变量(导入前需要将字符型转为整数型,并且需要声明类别型特征的字段名),它没有对类别型特征进行独热编码,因此速度比独热编码快得多。LightGBM使用了一个特殊的算法来确定属性特征的分割值。基本思想是对类别按照与目标标签的相关性进行重排序,具体一点是对于保存了类别特征的直方图根据其累计值(sum_gradient/sum_hessian)重排序,在排序好的直方图上选取最佳切分位置。
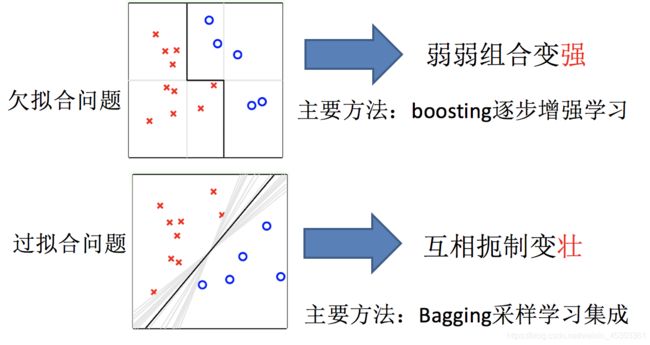
bagging集成与boosting集成的区别
boosting解决欠拟合问题,通过多个小模型 逐步增强学习 分段拟合Bagging解决过拟合问题,通过多个小模型 对同一模型投票 ,相互遏制变强
- 区别一:数据方面
Bagging:对数据进行采样训练;Boosting:根据前一轮学习结果调整数据的重要性。
- 区别二:投票方面
Bagging:所有学习器平权投票;Boosting:对学习器进行加权投票。
- 区别三:学习顺序
Bagging学习是并行,每个学习器没有依赖关系;Boosting学习是串行,学习有先后顺序。
- 区别四:小模型类别
Bagging中的模型是 强模型(偏差低,方差高)boosting中的模型是 弱模型(偏差高,方差低)
- 区别四:主要作用
Bagging主要用于提高泛化性能(解决过拟合,也可以说降低方差)Boosting主要用于提高训练精度 (解决欠拟合,也可以说降低偏差)
超参数确定
交叉验证 和 网格搜索
交叉验证:将数据分成n份,一份作为验证集。经 n 次(组)测试,每次都更换验证集。即得到 n次 模型结果,取平均值作为最终结果
作用:使获得的模型结果更准确,不优化模型

网格搜索:为超参数指定多个值,轮训训练模型,从而获取其中最优的参数和最佳模型
sklearn API:sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
参数:
estimator:实例化的估计器对象param_grid:估计器需要的参数字典{"参数1":[值1,值2,值3], "参数2":[值1,值2,值3],...}cv:指定几折交叉验证(与训练集和测试集比例有关,4 为 7.5:2.5)
结果分析:
模型训练结果.best_score_:在交叉验证中验证的最好结果模型训练结果.best_estimator_:最好的参数模型模型训练结果.cv_results_:查看所有模型的每次交叉验证结果