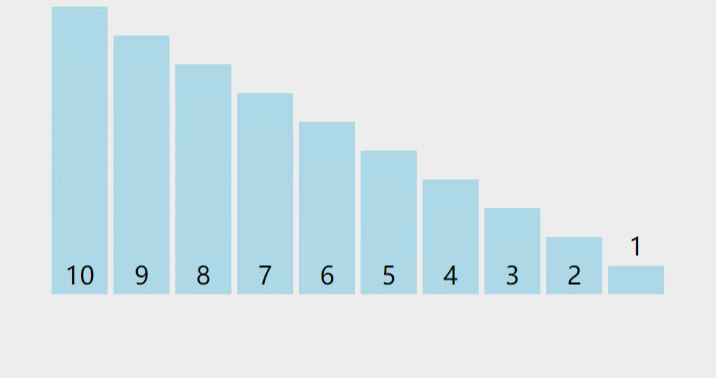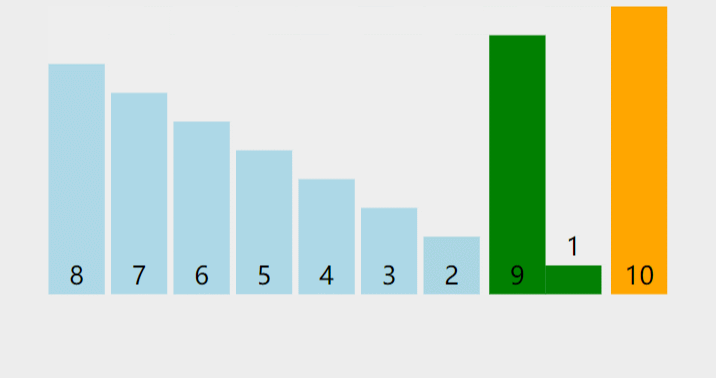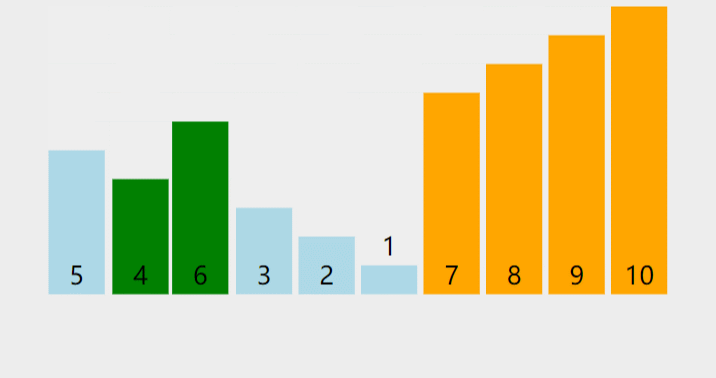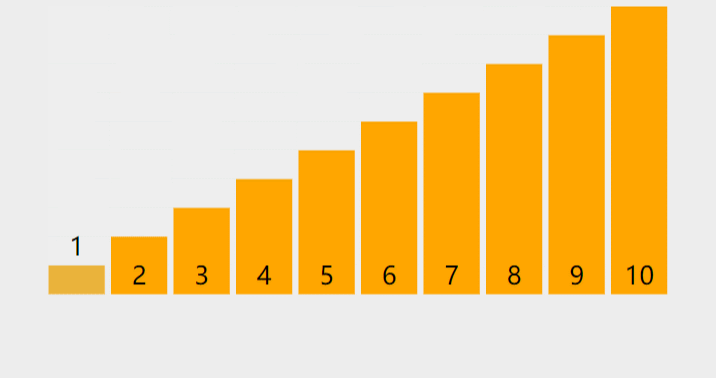数据结构算法---八大排序
目录
冒泡排序
插入排序
希尔排序
选择排序
堆排序
计数排序
归并排序
快速排序
源码
一般使用的八大排序算法是:插入排序、选择排序、冒泡排序、希尔排序、归并排序、快速排序、堆排序、计数排序。
内部排序:排序期间元素全部存放在内存中的排序;
外部排序:排序期间元素无法全部存放在内存中,必须在排序过程中根据要求不断地进行内外存之间移动地排序;
(这八种排序算法中除了归并排序是外部排序,其他都是内部排序)
冒泡排序
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。 它重复地走访过要排序的元素列,依次比较两个相邻的元素
冒泡排序算法思想较为简单,对每个下标i,取j从0到n-1-i(n是数组长度)进行遍历,如果两个相邻的元素s[j]>s[j+1],就交换。
这样每次最大的数则移动到了最后。
注:此动图来源与:百度
void BubbleSort(int* a, int n)//冒泡排序
{
int i, j;
for (i = 0; i <=n; i++)
{
for (j = 0; j < n - i-1; j++)//当i==n时 j+1 会越界 所以需要-1控制边界
{
if (a[j] > a[j + 1])//当前一个j大于后一个i时
{
Swap(&a[j], &a[j + 1]);//交换
}
}
}
}冒泡排序优点:稳定,且每次排序后,都有一个元素能确定正确位置
插入排序
插入排序,一般也被称为直接插入排序。 对于少量元素的排序,它是一个有效的算法
它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表
注:此动图来源与:百度
void InsertSort(int* a,int n)//插入排序
{
int i;
for (i = 0; i < n - 1;i++)
{
int end = i;//end在第i个
int tmp=a[end + 1];//tmp在end+1个
while (end >= 0)//当end小于0时结束循环
{
if (a[end] > tmp)//当前面的end大于后面的tmp时
{
a[end + 1] = a[end];//让end往后赋值
--end;//end往前移动1个位置 去找前一个是否比后面大(直到end比后面的值小时结束循环)
}
else
{
break;
}
}
a[end + 1] = tmp;//结束循环后在end后赋值tmp
}
}插入排序优点: 1.稳定,2.最坏情况下比较n*(n-1)/2次,最好情况下比较n-1次; 3.第k次排序后,前k个元素已经是从小到大排好序的
希尔排序
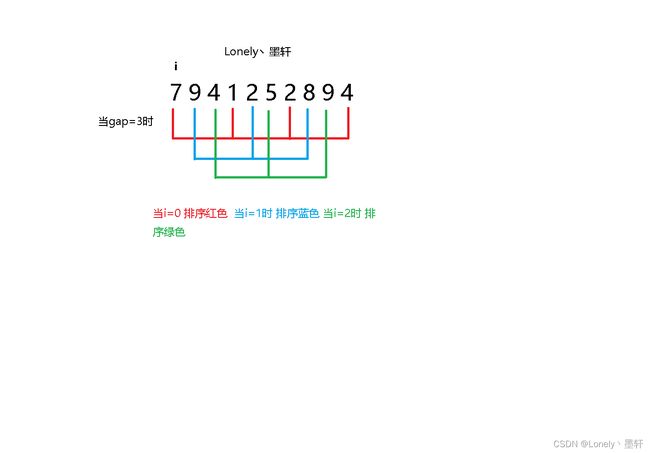
希尔排序是基于插入排序的一种排序算法,思想是对长度为n的数组s,每趟排序基于间隔h分成几组,对每组数据使用插入排序方法进行排序,然后减小h的值,这样刚开始时候虽然分组比较多,但每组数据很少,h减小后每组数据多但基本有序,而插入排序对已经基本有序的数组排序效率较高.
当gap=1时 那么它就是插入排序
void ShellSort(int* a, int n)//希尔排序
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
int i;
for (i = 0; i < n - gap; i++)
{
int end = i;//end在第i个位置
int tmp = a[end + gap];//tmp在第end+gao个位置
while (end >= 0)//当end小于0时结束循环
{
if (a[end] > tmp)//当前面的end大于后面的tmp时
{
a[end + gap] = a[end];//让end往后赋值
end -= gap;//end往前移动gap个位置 去找前一个是否比后面大(直到end比后面的值小时结束循环)
}
else
{
break;
}
}
a[end + gap] = tmp;//结束循环后在end+gap的位置赋值tmp
}
}
}希尔排序优点:每次排序都有预排序,排序执行效率比,插入,冒泡高,但是当数据是有序时,希尔排序的预排序等于每排,所以当数据有序时,去用希尔,反而不尽人意,当这种例子比较少,所以希尔排序还是不错的。
但稳定性:不稳定
选择排序
此排序对其进行优化,普通简单排序思想是:在第n个元素中,选最小,放在第一个位置,再选此小,放在第二个位置。
优化过后的选择排序思想:每次在n个元素中,选最小,与最大,把他们放入第一个为与最后一个位置,以此反复,效率比原来简单选择排序高不少
void SelecSort(int* a, int n)//选择排序
{
int left = 0, right = n - 1;
while (left < right)
{
int min = left, max = left;
int i;
for (i = left+1; i <= right; i++)
{
if (a[i] < a[min])
{
min = i;
}
if (a[i] > a[max])
{
max = i;
}
}
Swap(&a[left], &a[min]);
if (left == max)
{
max = min;
}
Swap(&a[right], &a[max]);
++left;
--right;
}
}选择排序优点:每次排序能确定两个元素的正确位置
当稳定性:不稳定
堆排序
堆排序是基于选择排序的一种排序算法,堆是一个近似完全二叉树的结构,且满足子结点的键值或索引总是小于(或者大于)它的父节点。这里采用最大堆方式:位于堆顶的元素总是整棵树的最大值,每个子节点的值都比父节点小,堆要时刻保持这样的结构,所以一旦堆里面的数据发生变化,要对堆重新进行一次构建。
简单来说,每次建大堆,堆顶一定是最大的数,把它放入堆的最后一个位置
并且下次建堆时,最后一个位置不参与建队。
第二次,堆顶次大的数放入倒数第二个位置,
并且下次建堆时,最后倒数第一和第二不参与建队。以此反复。
void ADjustDwom(int* a, int n, int root)//向下调整法
{
int prent = root;
int child = prent * 2 + 1;
while (child < n)
{
if (child + 1 < n&&a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[prent])
{
Swap(&a[prent], &a[child]);
prent = child;
child = prent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)//堆排序
{
int i;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
ADjustDwom(a, n, i);
}
int end = n-1;
while (end > 0)
{
Swap(&a[0], &a[end]);
ADjustDwom(a, end, 0);
--end;
}
}堆排序的优点:时间复杂度较好
但稳定性:不稳定,每次都要不断建堆
计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数
大致为遍历数组,选最大与最小,确定数组边界。在分别记录在开辟的新空间内,在按顺序放入原数组中
注:此动图来源与:百度
void CountSort(int* a, int n)//计数排序
{
int i;
int min = a[0], max = a[0];//
for (i = 1; i < n; i++)//选出最大与最小的数,确定边界
{
if (a[i] < min)
{
min = a[i];
}
if (a[i] > max)
{
max = a[i];
}
}
int range = (max-min) + 1;//创建相应的数组
int* count=(int*)malloc(sizeof(int)*range);//创建相应的数组
assert(count);
memset(count, 0, sizeof(int)*range);//将新数组内元素全部置0
for (i = 0; i < n; i++)//相对映射 第数组第0个数据 数组中数据为555 (最小的数为500)那么它为555-500=55,
//把55放入新数组的第0个位置
{
count[a[i] - min]++;
}
int j = 0;
for (i = 0; i < range; i++)
{
while (count[i]--)//当重复时 会记录重复几次 需要这个数重复的数持续放入,直到没有位置(那么就是0)(当为0结束)
{
a[j++] = i + min;//原来是 i-min 那么复原就是i+min
}
}
}计数排序的优点:对于确定且集中的数据有更加优秀的效率。
但稳定性:不稳定,对于松散的数据排序效率较差。
归并排序
递归版本
void _MergeSort(int* a, int left, int right,int* tmp)//归并递归
{
if (left >= right)
return;
int key = (right + left) / 2;
_MergeSort(a, left, key, tmp);//不断递归选出左区间与右区间
_MergeSort(a, key + 1, right, tmp);//直到递归到不可在划分的区间
int begin1 = left, end1 = key;
int begin2 = key + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)//选出左区间与右区间后 将他们进行排序
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)//当某区间没有完全放入新空间时 让它们继续放入
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));//把新空间的东西放回远数组中
}
void MergeSort(int* a, int n)//归并
{
int* tmp = (int*)malloc(sizeof(int)*n);//创建新空间
assert(tmp);
_MergeSort(a, 0, n - 1, tmp);//划分边界
free(tmp);//释放新数组
}归并非递归版本
void MergeSortNonR(int* a, int n)//归并非递归
{
int* tmp = (int*)malloc(sizeof(int)*n);
assert(tmp);
int gap = 1;
while(gap= n)//会出现边界问题时 让他们修正边界
{
end1 = n - 1;
}
if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
if (begin1 < n&&end2 >= n)
{
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
}
memcpy(a, tmp, n * sizeof(int));//把新空间内的数据放入远数组
gap *= 2;//增大gap 增大区间 让他们在新区间从新排序
}
free(tmp);//释放新空间
} 归并排序的思想是将两个有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。即先划分为两个部分,最后进行合并。
递归与非递归的区别在于:
递归是从大区间不断划分到小区间 直到划分到不可再分的小区间时,再返回将他们从小区间合并,再排序
上图是递归版本:
而非递归版本是从不可划分的小区间直到大区间,每次划分区间都在进行排序
快速排序
快速排序是内排序中平均性能较好的排序,思想是每趟排序时选取一个数据(通常用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它的左边,所有比它大的数都放到它的右边.
快速排序三种版本都是不断选key,然后递归。
hoare版本
1.选key(通常选最左边的值) 让left从最左边开始,right从最右边开始。(因为递归栈帧问题,left与right都是直接调用参数查找,不运行再创建临时变量结束left与right)
2.若key选最左值 那么让right先开始。若key选最右值 让left先开始
3.left负责找比key大的值,right负责找比key大的值
4.当left与right都找到了相应的值时,让left与right的所指的值想换。然后不断重复
直到left与right相遇时 停下
5.停下后, 让key的值与left(即left与right相遇的位置)交换。最后返回left
因为文字描述实在不好理解,所以我干脆都放入图中讲解。
int parsont1(int* a, int left, int right)//hoare法版本
{
int key = left;
while (left < right)
{
while (left < right&&a[right] >= a[key])
--right;
while (left < right&&a[left] <= a[key])
++left;
Swap(&a[left], &a[right]);
}
Swap(&a[key], &a[left]);
return left;
}
void QuickSort(int* a, int left,int right)//快速排序
{
if (left >= right)
return;
int key = parsont1(a,left,right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}挖坑法版本
挖坑法思想:
1选key 通常选最左值 再选左边为坑位。left与right分别找比key大和比key小的值。
2先让right寻找比key小的值,当找到时 把right的值放入坑位后,再让坑位更新为right的位置。
3再让让left寻找比key大的值,当找到时 把left的值放入坑位后,再让坑位更新为left的位置。
4当left与right相遇时 最后会剩下最后一个坑 把key的值放入坑中。
5最后返回坑位的值
int parsont2(int* a, int left, int right)//挖坑法版本
{
int key = a[left];
int pit = left;
while (left < right)
{
while (left < right&&a[right] >= key)
{
--right;
}
a[pit] = a[right];
pit = right;
while (left < right&&a[left] <= key)
{
++left;
}
a[pit] = a[left];
pit = left;
}
a[pit] = key;
return pit;
}
void QuickSort(int* a, int left,int right)//快速排序
{
if (left >= right)
return;
int key = parsont2(a,left,right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}前后指针法版本
此版本是三个版本是最好理解,且代码更简洁的版本,并且思路较为清晰,推荐使用此版本。
前后指针思想:
1.key的值选最左值。
2.prve最开始为第一个位置 cur最开始为第二个位置
3.cur去找比key小的值 当找到时,先让prve++ ,再让cur的值与prve的值交换
4.当没找到时 cur++
5.当cur大于原数据时 把prve的值与key的值交换,最后返回prve的值
int parsont3(int* a, int left, int right)//前后指针法版本
{
int prve = left;
int cur = left + 1;
int key = left;
while (cur <= right)
{
if (a[cur] < a[key] && a[++prve] != a[cur])//当cur找到比key小的值时 先让prve++ 若prve的位置与cur的位置重叠 那么不交换
//因为prve的位置与cur的位置重叠时,交换是没有意义的。当他们不重叠时 再交换
{
Swap(&a[prve], &a[cur]);
}
++cur;//当没找到或者交换过后 都++prve
}
Swap(&a[prve], &a[key]);//当循环结束时 交换prve与key的值
return prve;//再返回prve位置的值
}
void QuickSort(int* a, int left,int right)//快速排序
{
if (left >= right)
return;
int key = parsont3(a,left,right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}快速排序非递归
因为递归对内存占用过大,所以我们也会给出非递归版本(跟归并非递归同样)
快速排序非递归思想:
1.先入栈:数据的边界
2.用right与left接收
3.再把right和left放入函数排序
4.之后划分区间,在选出区间的边界,继续调用函数排序(三种版本均可取)
5.直到栈为空时。结束
这把需要用到栈的思想 若不懂栈可以取看看这篇:C语言---栈(详解)---数据结构
void QuickSortNonR(int* a, int left, int right)//快速排序非递归
{
ST st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
//因为栈是先入后出 又因为是左边界先入右边界再入 所以取栈顶元素 是出右边边界 所以我们用right接收
int right = StackTop(&st);//取栈顶元素 用right接收
StackPop(&st);//出栈顶元素
int left = StackTop(&st);//再取栈顶元素 用left接收
StackPop(&st);//出栈顶元素
int key = parsont3(a, left, right);//用刚接收的边界 取调用三种版本算法排序
if (left < key - 1)//当左区间还是可以再划分的区间时
{
StackPush(&st, left);//取他们的边界
StackPush(&st, key-1);
}
if (key + 1 < right)//当右边界还是可以再划分的区间时
{
StackPush(&st, left);//取他们的边界
StackPush(&st, key - 1);//之后继续循环
}
}
StackDestroy(&st);//当栈为空时 排序完成的 继续销毁栈
}若需要栈的源码 待会我会放在文章下面
快速排序总结:
1.不稳定;
2.快速排序过程中不会产生有序子序列,但每一趟排序后都有一个元素放在其最终位置上;
3.每次选择的关键值可以把数组分为两个子数组的时候,快速排序算法的速度最快,当数组已经是正序或逆序时速度最慢;
4.递归次数与每次划分后得到的分区的处理顺序无关;
5.对n个关键字进行快速排序,最大递归深度为n,最小递归深度为log2n;
源码
排序实现
#include"sort.h"
#include"栈.h"
void Swap(int* q, int* p)
{
int tmp = *q;
*q = *p;
*p = tmp;
}
void Print(int* a, int n)//打印
{
int i;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void InsertSort(int* a,int n)//插入排序
{
int i;
for (i = 0; i < n - 1;i++)
{
int end = i;//end在第i个
int tmp=a[end + 1];//tmp在end+1个
while (end >= 0)//当end小于0时结束循环
{
if (a[end] > tmp)//当前面的end大于后面的tmp时
{
a[end + 1] = a[end];//让end往后赋值
--end;//end往前移动1个位置 去找前一个是否比后面大(直到end比后面的值小时结束循环)
}
else
{
break;
}
}
a[end + 1] = tmp;//结束循环后在end后赋值tmp
}
}
void ShellSort(int* a, int n)//希尔排序
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
int i;
for (i = 0; i < n - gap; i++)
{
int end = i;//end在第i个位置
int tmp = a[end + gap];//tmp在第end+gao个位置
while (end >= 0)//当end小于0时结束循环
{
if (a[end] > tmp)//当前面的end大于后面的tmp时
{
a[end + gap] = a[end];//让end往后赋值
end -= gap;//end往前移动gap个位置 去找前一个是否比后面大(直到end比后面的值小时结束循环)
}
else
{
break;
}
}
a[end + gap] = tmp;//结束循环后在end+gap的位置赋值tmp
}
}
}
void BubbleSort(int* a, int n)//冒泡排序
{
int i, j;
for (i = 0; i <=n; i++)
{
for (j = 0; j < n - i-1; j++)//当i==n时 j+1 会越界 所以需要-1控制边界
{
if (a[j] > a[j + 1])//当前一个j大于后一个i时
{
Swap(&a[j], &a[j + 1]);//交换
}
}
}
}
void _MergeSort(int* a, int left, int right,int* tmp)//归并递归
{
if (left >= right)
return;
int key = (right + left) / 2;
_MergeSort(a, left, key, tmp);//不断递归选出左区间与右区间
_MergeSort(a, key + 1, right, tmp);//直到递归到不可在划分的区间
int begin1 = left, end1 = key;
int begin2 = key + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)//选出左区间与右区间后 将他们进行排序
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)//当某区间没有完全放入新空间时 让它们继续放入
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));//把新空间的东西放回远数组中
}
void MergeSort(int* a, int n)//归并
{
int* tmp = (int*)malloc(sizeof(int)*n);//创建新空间
assert(tmp);
_MergeSort(a, 0, n - 1, tmp);//划分边界
free(tmp);//释放新数组
}
void MergeSortNonR(int* a, int n)//归并非递归
{
int* tmp = (int*)malloc(sizeof(int)*n);
assert(tmp);
int gap = 1;
while(gap= n)//会出现边界问题时 让他们修正边界
{
end1 = n - 1;
}
if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
if (begin1 < n&&end2 >= n)
{
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
}
memcpy(a, tmp, n * sizeof(int));//把新空间内的数据放入远数组
gap *= 2;//增大gap 增大区间 让他们在新区间从新排序
}
free(tmp);//释放新空间
}
void SelecSort(int* a, int n)//选择排序
{
int left = 0, right = n - 1;
while (left < right)
{
int min = left, max = left;
int i;
for (i = left+1; i <= right; i++)
{
if (a[i] < a[min])
{
min = i;
}
if (a[i] > a[max])
{
max = i;
}
}
Swap(&a[left], &a[min]);
if (left == max)
{
max = min;
}
Swap(&a[right], &a[max]);
++left;
--right;
}
}
void ADjustDwom(int* a, int n, int root)//向下调整法
{
int prent = root;
int child = prent * 2 + 1;
while (child < n)
{
if (child + 1 < n&&a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[prent])
{
Swap(&a[prent], &a[child]);
prent = child;
child = prent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)//堆排序
{
int i;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
ADjustDwom(a, n, i);
}
int end = n-1;
while (end > 0)
{
Swap(&a[0], &a[end]);
ADjustDwom(a, end, 0);
--end;
}
}
int parsont1(int* a, int left, int right)//hoare法版本
{
int key = left;
while (left < right)
{
while (left < right&&a[right] >= a[key])
--right;
while (left < right&&a[left] <= a[key])
++left;
Swap(&a[left], &a[right]);
}
Swap(&a[key], &a[left]);
return left;
}
int parsont2(int* a, int left, int right)//挖坑法版本
{
int key = a[left];
int pit = left;
while (left < right)
{
while (left < right&&a[right] >= key)
{
--right;
}
a[pit] = a[right];
pit = right;
while (left < right&&a[left] <= key)
{
++left;
}
a[pit] = a[left];
pit = left;
}
a[pit] = key;
return pit;
}
int parsont3(int* a, int left, int right)//前后指针法版本
{
int prve = left;
int cur = left + 1;
int key = left;
while (cur <= right)
{
if (a[cur] < a[key] && a[++prve] != a[cur])//当cur找到比key小的值时 先让prve++ 若prve的位置与cur的位置重叠 那么不交换
//因为prve的位置与cur的位置重叠时,交换是没有意义的。当他们不重叠时 再交换
{
Swap(&a[prve], &a[cur]);
}
++cur;//当没找到或者交换过后 都++prve
}
Swap(&a[prve], &a[key]);//当循环结束时 交换prve与key的值
return prve;//再返回prve位置的值
}
void QuickSort(int* a, int left,int right)//快速排序
{
if (left >= right)
return;
int key = parsont3(a,left,right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
void QuickSortNonR(int* a, int left, int right)//快速排序非递归
{
ST st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
int right = StackTop(&st);
StackPop(&st);
int left = StackTop(&st);
StackPop(&st);
int key = parsont3(a, left, right);
if (left < key - 1)
{
StackPush(&st, left);
StackPush(&st, key-1);
}
if (key + 1 < right)
{
StackPush(&st, left);
StackPush(&st, key - 1);
}
}
StackDestroy(&st);
}
void CountSort(int* a, int n)//计数排序
{
int i;
int min = a[0], max = a[0];//
for (i = 1; i < n; i++)//选出最大与最小的数,确定边界
{
if (a[i] < min)
{
min = a[i];
}
if (a[i] > max)
{
max = a[i];
}
}
int range = (max-min) + 1;//创建相应的数组
int* count=(int*)malloc(sizeof(int)*range);//创建相应的数组
assert(count);
memset(count, 0, sizeof(int)*range);//将新数组内元素全部置0
for (i = 0; i < n; i++)//相对映射 第数组第0个数据 数组中数据为555 (最小的数为500)那么它为555-500=55,
//把55放入新数组的第0个位置
{
count[a[i] - min]++;
}
int j = 0;
for (i = 0; i < range; i++)
{
while (count[i]--)//当重复时 会记录重复几次 需要这个数重复的数持续放入,直到没有位置(那么就是0)(当为0结束)
{
a[j++] = i + min;//原来是 i-min 那么复原就是i+min
}
}
} 排序声明
#pragma once
#include
#include
#include
#include
#include
void InsertSort(int* a,int n);//插入排序
void ShellSort(int* a, int n);//希尔排序
void BubbleSort(int* a, int n);//冒泡排序
void MergeSort(int* a, int n);//归并
void MergeSortNonR(int* a, int n);//归并非递归
void SelecSort(int* a, int n);//选择排序
void HeapSort(int* a, int n);//堆排序
void QuickSort(int* a, int left,int right);//快速排序
void QuickSortNonR(int* a,int left,int right);//快速排序非递归
void CountSort(int* a, int n);//计数排序
void Print(int* a, int n);//打印
排序功能调用
#include"sort.h"
int main()
{
int a[] = { 5,8,2,7,1,9,5,0,4,2};
int n = sizeof(a) / sizeof(int);
//InsertSort(a, n);//插入排序
//Print(a,n);
//ShellSort(a, n);//希尔排序
//Print(a, n);
//BubbleSort(a, n);//冒泡排序
//Print(a, n);
//MergeSort(a, n);//归并*
//Print(a, n);
//MergeSortNonR(a, n);//归并非递归*
//Print(a, n);
//SelecSort(a, n);//选择排序
//Print(a, n);
//HeapSort(a, n);//堆排序
//Print(a, n);
//QuickSort(a, 0, n - 1);//快速排序
//Print(a, n);
//QuickSortNonR(a, 0, n - 1);//快速非递归
//Print(a, n);
//CountSort(a, n);//计数排序
//Print(a, n);
return 0;
}栈的声明
#pragma once
typedef int STDataType;
typedef struct Stack
{
STDataType* a;//存放数据
int top;//指向栈顶元素
int capacity;//容量大小
}ST;
void StackInit(ST* ps);
void StackPush(ST* ps, STDataType data);
void StackPop(ST* ps);
STDataType StackTop(ST* ps);
bool StackEmpty(ST* ps);
int StackSize(ST* ps);
void StackDestroy(ST* ps);栈的实现
#include"sort.h"
#include"栈.h"
void StackInit(ST* ps)//初始化栈
{
ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);
ps->top = 0;
ps->capacity = 4;
}
void StackPush(ST* ps, STDataType data)//入栈
{
assert(ps);
if (ps->top == ps->capacity)
{
STDataType* tmp = (STDataType*)realloc(ps->a, ps->capacity * 2 * sizeof(STDataType));
ps->a = tmp;
ps->capacity *= 2;
}
ps->a[ps->top] = data;
ps->top++;
}
void StackPop(ST* ps)//出栈
{
assert(ps);
assert(ps->top);
ps->top--;
}
STDataType StackTop(ST* ps)//返回栈顶元素
{
assert(ps);
return ps->a[ps->top - 1];
}
bool StackEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
int StackSize(ST* ps)
{
assert(ps);
return ps->top;
}
void StackDestroy(ST* ps)
{
free(ps->a);
ps->a = NULL;
ps->top = ps->capacity = 0;
}若本篇文章对您有帮助,希望能获得您的赞!