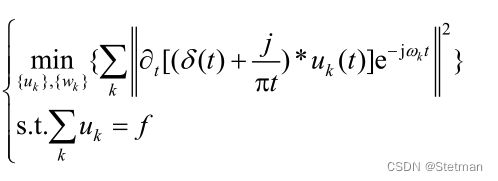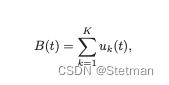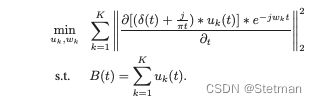变分模态分解（VMD）与其改进算法

        之前参加课题组相关信号处理的课题的学习笔记。

        变分模态分解(variational mode decomposition)VMD是2014年提出的一种非递归信号处理方法，通过将时间序列数据分解为一系列具有有限带宽的本征模态函数(IMF)，迭代搜寻变分模态的最优解。VMD可以自适应更新各IMF的最优中心频率和带宽。

        相较于EMD，VMD具有更强大的性能：在进行EMD分解时，我们需要利用信号的极大值和极小值来计算包络，而信号的极值很有可能收到噪声干扰，因此EMD对噪声比较敏感；EMD还存在端点效应的问题，即在信号的端点处由于没有前后帧的信息，求得的包络面可能不准确，在后期分解的过程中，可能会得到不准确的IMF分量。而VMD不存在这方面问题，其具有较好抗噪能力，能解决频率混叠问题。

VMD原理

        VMD实际上是将分解过程转化为了优化过程，其过程是变分问题的求解过程，该算法可分为变分问题的构造和求解。

变分问题构造：

变分问题求解：

引入二次惩罚因子α和拉格朗日乘法算子λ(t)，将约束性变分问题变为非约束性变分问题：

采用了乘法算子交替方向法(alternate direction method of multipliers)ADMM 解决以上变分问题，通过交替更新计算，求扩展拉格朗日表达式的‘鞍点’：

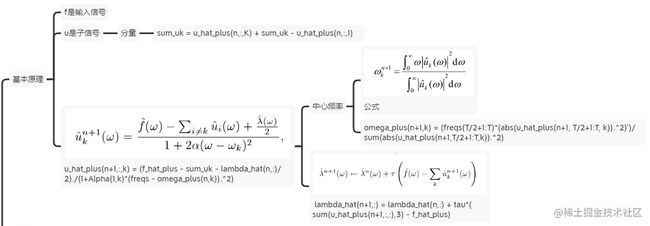
总体整合如下：

VMD使用

在python中可以装载vmdpy，从中调用VMD函数：

from vmdpy import VMD
u, u_hat, omega = VMD(signal, alpha, tau, K, DC, init, tol)

在 VMD 分解函数中，signal即为转化为一维的待分解信号，

以下为参数，可以调整以获得更好的分解效果：

alpha：这是带宽约束参数。增加 alpha 值会使分解的模态更加平滑，但也可能导致过度平滑和模态混合。减小 alpha 值会使分解的模态更加锐利，但也可能导致噪声增强和虚假模态出现。

tau：这是噪声容忍度参数。增加 tau 值会使算法对噪声更加容忍，从而减少虚假模态的出现。但是，过大的 tau 值也可能导致真实模态被忽略。

K：这是模态数量参数。选择合适的 K 值非常重要，因为它决定了分解结果中包含多少个模态。如果 K 值过小，则可能导致多个真实模态被混合在一起；如果 K 值过大，则可能导致虚假模态的出现。

DC：这是直流分量参数。如果信号中包含直流分量，则应将此参数设置为 1；否则应将其设置为 0。

init：这是初始频率估计方法参数。可以选择均匀初始化（init=1）或随机初始化（init=2）。

tol: 这是收敛容差参数。减小此值可以使算法收敛到更精确的结果，但也会增加计算时间。

调整这些参数需要根据具体信号特点和分析需求进行试验和比较

返回值中：

 u: 分解后的模态信号，二维 numpy 数组，每行为一个模态信号。

u_hat： 不同模态的频谱

 omega: 模态中心频率随时间变化的轨迹，二维 numpy 数组，每行为一个模态中心频率轨迹。

 可以进一步封装此函数，写一个简单的脚本：

from typing import Tuple
import numpy as np
from vmdpy import VMD


def vmd_decomposition(signal: np.ndarray, K: int) -> Tuple[np.ndarray, np.ndarray]:
    # 设置 VMD 参数
    alpha = 2000  # moderate bandwidth constraint
    tau = 0.  # noise-tolerance (no strict fidelity enforcement)
    DC = 0  # no DC part imposed
    init = 1  # initialize omegas uniformly
    tol = 1e-7  # convergence tolerance

    # 进行 VMD 分解
    u, u_hat, omega = VMD(signal, alpha, tau, K, DC, init, tol)

    return u, omega

如果要依据VMD进行重构，即为将每个预测的IMF信号直接进行叠加。

改进VMD算法

 在之前阅读的论文中，有两篇使用了改进VMD：

DetectDUI: An In-Car Detection System for Drink Driving and BACs

作者认为VMD虽然通过非递归解决了EMD易被噪音干扰的问题，然而，分解模式的数量影响每个模式的中心频率和窄带宽，导致呼吸和心跳的检测精度降低。因此，作者提出了自适应变分模态分解，来自适应地确定分解模式的数量：

首先，AVMD将时间序列信号B（t）分解为K个子信号,（模式）通过固有模式函数（IMF），其中uk（t）是第k个模式

与传统的VMD算法类似，AVMD需要三个步骤来估计每个IMF的带宽。首先，计算每个模式的分析信号。然后，将这些模式与指数相混合，以将它们的频率转移到基带。最后，通过梯度的平方L2范数来估计每个模式的带宽。约束变分问题可以表示为 ：

 = -1 ,wk是模式uk（t）的中心频率。

整体算法如下：

第3行和第4行更新模式及其中心频率。在方程（7）中，ξb（ω）是滤波信号的频域表示。λ是二次罚项[34]。α是白噪声的方差。在第5行中计算uõk的希尔伯特变换，在此基础上，在第6行中计算瞬时频率uif（k），在第7行中计算平均瞬时频率mif（k）。根据第8行中的mif（k）导出曲率IC。处罚期限,λ在第11行中基于更新率β进行更新，收敛条件在第12行中给出。

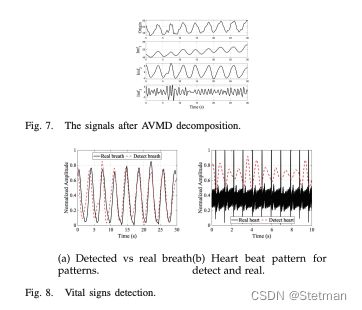
 文章给出的效果展示：

V2 iFi: in-Vehicle Vital Sign Monitoring via Compact RF Sensing

作者基于前人的工作，认为摄像机会侵犯个人隐私、声信号对宠物与婴儿不友好且易于被背景影响、wifi信号在狭小多人环境下很难提取出每个人的信号，因此选取了RF射频信号作为监控驾驶疲劳的信号。

文中，在通过峰值等方法实现了不同乘车人信号的区分后，即面临对于信号分离方面的问题。文中认为此时信号为驾驶员心跳、呼吸、车辆震动、驾驶员动作的混合信号，对于这种情况的信号分离工作，VMD再合适不过。然而，VMD只支持单一信号序列，而单一信号不足以提取生命体征。因此，作者改进该算法，提出了一种多序列VMD算法：MS-VMD算法（如下图）。

 

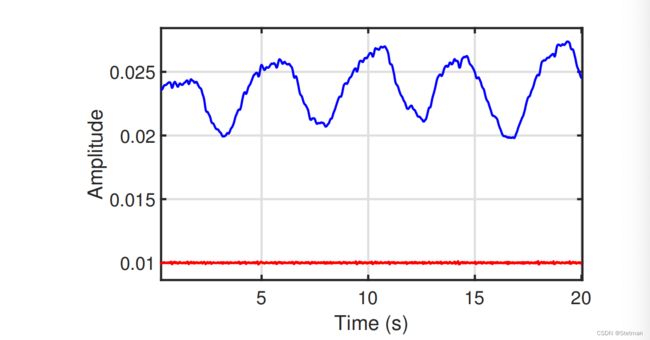
 分解效果：蓝线即为所求