数据结构——树
数据结构笔记目录:
1. 绪论、时间复杂度
2. 线性表
3. 树
4. 图
5. 查找
6. 排序
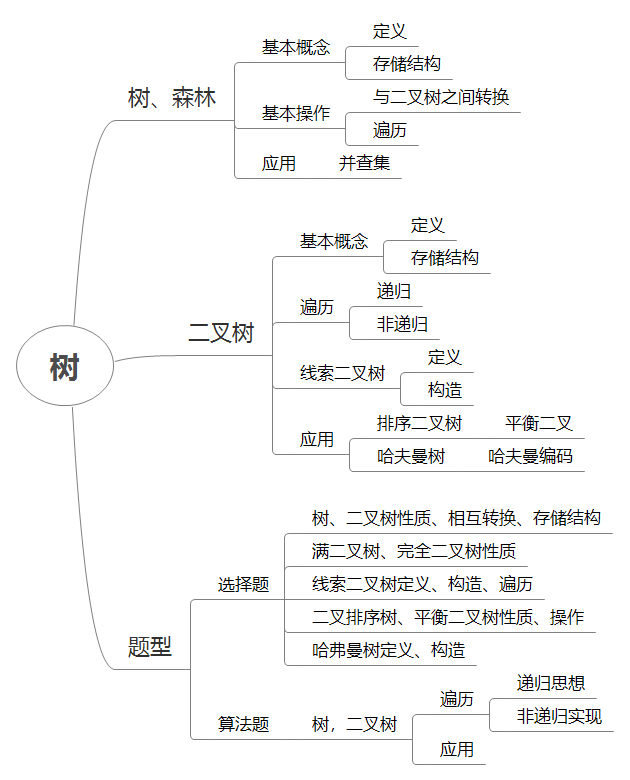
3.1 树
3.1.2 基本定义
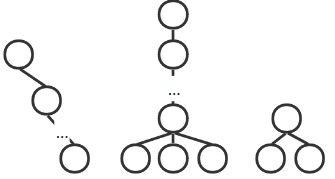
n 个结点的有限集( n ≥ 0 n \ge 0 n≥0 )
- 每棵树只有一个根结点
- 其余结点分为 m 个有限集,每个有限集都是树
1. 定义
逻辑结构
一对多 :除根结点外,其余节点有且仅有一个前驱,可以有多个后缀
层次结构
树中某节点最多只和上一层的一个结点有直接关系 ⟹ \Longrightarrow ⟹ n个结点 n-1 条边
2. 术语
结点间关系
路径:从根到孩子结点 间经过的结点序列
-
树:无序有向 方向由双亲结点指向孩子结点
-
从根到某一结点的 路径 只有一条
-
路径长度:序列中结点个数
度
一个双亲结点有几个孩子结点
-
分支结点度 > 0
-
叶子结点的度 = 0
-
树的度指的是树中最大的结点度
区分
| 度为m的树 | m叉树 |
|---|---|
| 至少有一个结点的度等于m | 允许所有结点的度都小于m |
| 不允许为空树 | 可以为空树 |
度的深度&高度
深度:自顶向下
高度:自底向上
- 树的高度/深度:从1开始,结点最大层数
有序树&无序树
有序树:子树左右次序不能互换
森林
m ( m ≥ 0 m\ge 0 m≥0) 个根,且结点不相交的有限结点集
3.1.3 性质
1. 树的第i层结点
度为m的树中第i层最多有 m i − 1 m^{i-1} mi−1 个结点
高为h的树中最多有 1 + m + m 2 + . . . + m h − 1 = m h − 1 m − 1 1+m+m^2+...+m^{h-1}=\frac{m^h-1}{m-1} 1+m+m2+...+mh−1=m−1mh−1
2. 树结点与度之间的关系
总结点数 = n 0 + n 1 + . . . + n m = 总分支数 + 1 又,总度数 = n 1 + 2 n 2 + m n m = 总分支数 故,总结点数 = 总度数 + 1 \begin{aligned} 总结点数&=n_0+n_1+...+n_m\\ & =总分支数+1\\ 又,总度数&=n_1+2n_2+mn_m=总分支数\\ 故,总结点数&=总度数+1 \end{aligned} 总结点数又,总度数故,总结点数=n0+n1+...+nm=总分支数+1=n1+2n2+mnm=总分支数=总度数+1
3. 结点数与高度的关系
具有n个结点的m叉树
- 最大高度为n
- 最小高度为 ⌈ l o g m [ ( m − 1 ) n + 1 ] ⌉ \lceil log_m[(m-1)n+1] \rceil ⌈logm[(m−1)n+1]⌉
推导
由第i层最多有 m i − 1 m^{i-1} mi−1 个结点,故深度为h的树结点数范围为
1 + m + m 2 + . . . + m h − 1 < n ≤ 1 + m + m 2 + . . . + m h − 1 m h − 1 − 1 m − 1 < n ≤ m h − 1 m − 1 m h − 1 − 1 < n ( m − 1 ) ≤ m h − 1 m h − 1 < n ( m − 1 ) + 1 ≤ m h 故 h − 1 < l o g m [ n ( m − 1 ) + 1 ] 且 h ≥ l o g m [ n ( m − 1 ) + 1 ] 即 h < ⌈ l o g m [ n ( m − 1 ) + 1 ] ⌉ \begin{aligned} 1+m+m^2+...+m^{h-1} &< \ n \le 1+m+m^2+...+m^h-1 \\\\ \frac{m^{h-1}-1}{m-1} &< \ n \le \frac{m^{h}-1}{m-1} \\\\ m^{h-1}-1 &< \ n(m-1) \le m^h-1 \\\\ m^{h-1} &< \ n(m-1)+1 \le m^h \\\\ 故h-1< log_m[n(m-1)+1]& \quad且 \quad h \ge log_m[n(m-1)+1] \\\\ 即h< \lceil log_m[n(m-1)+1] \rceil& \end{aligned} 1+m+m2+...+mh−1m−1mh−1−1mh−1−1mh−1故h−1<logm[n(m−1)+1]即h<⌈logm[n(m−1)+1]⌉< n≤1+m+m2+...+mh−1< n≤m−1mh−1< n(m−1)≤mh−1< n(m−1)+1≤mh且h≥logm[n(m−1)+1]
3.1.4 树的存储结构
能唯一反映树中各结点之间的逻辑关系
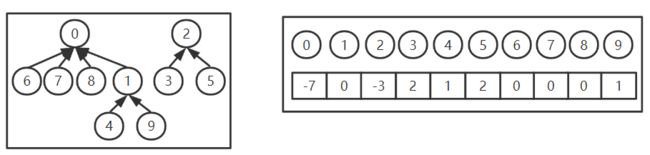
1. 双亲表示法
顺序存储 :利用结点只有唯一双亲结点,每个结点中增设伪指针指向双亲结点所在存储位置
- 便于得到双亲结点 O ( 1 ) O(1) O(1)
- 求结点的孩子结点需要遍历整个存储结构 O ( n ) O(n) O(n)
表示
typedef struct{
ElemType data;
int parent;
}PTNode;
typedef struct{
PTNode nodes[MaxSize];
int n;
}PTree;
- 根结点下标为0;其双亲域为-1
2. 孩子表示法
拉链法 :将每个结点的孩子用单链表链接
- 除叶结点,有多少个其余节点就有多少个链表
- 便于寻找孩子结点 O ( 1 ) O(1) O(1)
- 寻找双亲结点需要遍历整个存储结构 O ( n ) O(n) O(n)
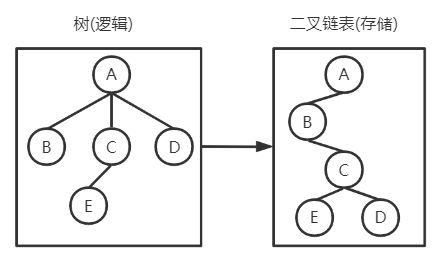
3. 孩子兄弟表示法
二叉链表 :左子树根为其左孩子结点;右子树根为左孩子结点的第一个相邻兄弟结点
struct CSNode{
ElemType data;
struct CSNode *firstChild,*nextSibling;
}CSNode;
- 利用树 → \rightarrow → 二叉树转化的思想
- 从当前节点查找其双亲结点复杂
- 可增设
parent域
- 可增设
3.1.5 树的操作
1. 树、森林与二叉树的转换
左子右兄 :给定一棵树或者一个森林 都有唯一的二叉树与之对应
- 可以理解为对同一棵二叉树的解释方式不同。若两个孩子结点表示
- 左右孩子,则为二叉树
- 左子右兄,则为其对应的树或森林
树 -> 二叉树
-
具有相同双亲的叶结点,转化后只剩一个叶结点 (最右叶结点)
-
每一层的最后一个结点转化为二叉树后其右指针域为空
-
叶结点个数 = 左指针域为空的结点数
森林 -> 二叉树
- 森林中每棵树 → \rightarrow → 二叉树
- 后一棵树为前一棵树的右子树
二叉树 -> 森林
- 根及左子树为第一棵树的二叉树形式
- 二叉树右子树为森林除第一棵树的二叉树形式
2. 树、森林遍历
树遍历
先序
-
访问根
-
先序遍历左子树
-
先序遍历右子树
后序
-
后序遍历左子树
-
后序遍历右子树
-
访问根
森林遍历
先序
-
访问根
-
先序遍历第一棵树的子树
-
先序除第一棵树的森林
中序
-
中序第一棵树的子树
-
访问第一棵树的根
-
中序除第一棵树的森林
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先序 | 先序 | 先序 |
| 后序 | 中序 | 中序 |
- 可以理解为对一棵二叉树遍历序列的解释方式不同
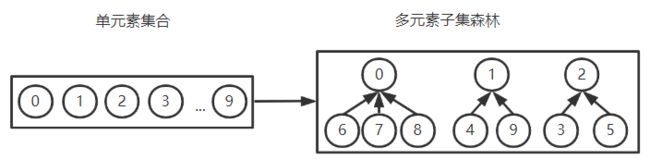
3.1.6 树的应用——并查集
1. 目标
2. 存储结构
顺序存储
- 子集根结点数据域: − ∣ 当前子集中元素个数 ∣ -\mid当前子集中元素个数\mid −∣当前子集中元素个数∣
- 孩子结点数据域:所在集合的根结点下标
3. 操作
3.1.7 常用特例
3.2 二叉树
3.2.1 基本概念
1. 定义
n( n ≥ 0 n\ge 0 n≥0) 个结点组成的有序树
- n=0,空二叉树
- n > 0 左右子树互不相交且分别是一棵二叉树
2. 特点
-
每个结点至多只有2棵子树
不是度为2的树
- 度为2的树至少有三个结点
- 二叉树可以是空树
-
二叉树是 有序树 ,区分左右
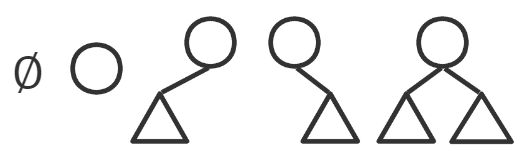
3. 五种基本形态
3.2.2 二叉树性质
-
n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1
任一棵树,边数=结点树-1
2 n 2 + n 1 = n 2 + n 1 + n 0 − 1 2n_2+n_1=n_2+n_1+n_0-1 2n2+n1=n2+n1+n0−1
-
第 k 层至多有 2 k − 1 2^{k-1} 2k−1 个结点(k ≥ \ge ≥ 1)
-
高为 h 的二叉树至多有 2 h − 1 2^{h}-1 2h−1 个结点
1. 满二叉树
除叶外,每个结点的度都为2
-
第 i 层结点数为第 i-1 层结点数的2倍
-
高为 h 的满二叉树,含有 2 h − 1 2^h-1 2h−1 个结点
- 树中总结点数n为奇数
2. 完全二叉树
满二叉树连续缺失最下最右叶结点
-
编号与对应满二叉树相同
-
结点 i 与其双亲结点、孩子结点编号的关系
{ i > 1 , 其双亲结点编号为 ⌈ i 2 ⌉ 2 i ≤ n , 其左孩子为 2 i 2 i + 1 ≤ n , 其右孩子为 2 i + 1 \begin{aligned} \begin{cases} i>1 &, 其双亲结点编号为 \lceil \frac{i}{2}\rceil \\ 2i \le n &, 其左孩子为2i\\ 2i+1 \le n &,其右孩子为2i+1 \end{cases} \end{aligned} ⎩ ⎨ ⎧i>12i≤n2i+1≤n,其双亲结点编号为⌈2i⌉,其左孩子为2i,其右孩子为2i+1
-
设编号为 i 的结点,若 i ≤ ⌊ n 2 ⌋ i \le \lfloor \frac{n}{2} \rfloor i≤⌊2n⌋ ,则结点 i 为分支结点,否则为叶子结点
-
设树的总结点数为n
-
若 n 为奇数,则每个分支结点都有左右孩子
-
若 n 为偶数,则编号为 n 2 \frac{n}{2} 2n 的结点只有左孩子
度为1的结点有且只有一个左孩子
-
树高为
⌈ l o g 2 ( n + 1 ) ⌉ 或 ⌊ l o g 2 n ⌋ + 1 \lceil log_2(n+1) \rceil 或\lfloor log_2n \rfloor+1 ⌈log2(n+1)⌉或⌊log2n⌋+1
-
-
编号为 i 的结点为叶结点或只有左孩子,则编号大于 i 的结点都是叶结点
结点总数与叶结点数关系
注:重点是推导思路,式子不重要
-
已知结点总数,求叶子结点数
设完全二叉树结点总数为n,由完全二叉树的性质,前 h-1 层共有 2 h − 1 − 1 2^{h-1}-1 2h−1−1 个结点,故叶子结点个数为 n − 2 h − 1 + 1 n-2^{h-1}+1 n−2h−1+1 。可知第 h-1 层有孩子结点的结点数为 $\lceil \frac{n-2^{h-1}+1}{2} \rceil $ ,而第 h-1 层有 2 h − 2 2^{h-2} 2h−2 个结点,故第 h-1 层的叶子结点数为$2^{h-2}-\lceil \frac{n-2^{h-1}+1}{2} \rceil $ 。故含n个结点的完全二叉树,叶子结点个数为 n + 1 − 2 h − 2 − ⌈ n − 2 h − 1 + 1 2 ⌉ n+1-2^{h-2}-\lceil \frac{n-2^{h-1}+1}{2} \rceil n+1−2h−2−⌈2n−2h−1+1⌉ 。
-
已知第h层有k个叶结点,求树中总结点数
-
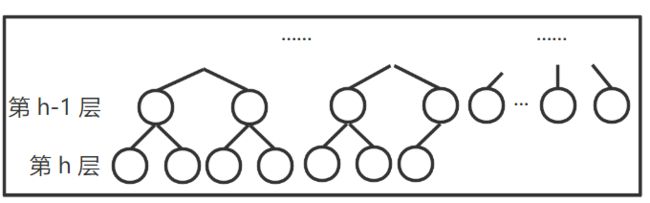
树中结点数最多情况:第 h 层满,且第 h+1 层还有叶结点,如下图。
第 h 层有孩子结点的分支结点数为 2 h − 1 − k 2^{h-1} - k 2h−1−k ,故树中结点总数为 2 h − 1 + 2 ( 2 h − 2 − k ) = 3 ∗ 2 h − 1 − 2 k − 1 2^h-1+2(2^{h-2}-k)=3*2^{h-1}-2k-1 2h−1+2(2h−2−k)=3∗2h−1−2k−1 或 3 ∗ 2 h − 1 − 2 k − 2 3*2^{h-1}-2k-2 3∗2h−1−2k−2
-
树中结点数最少情况:第 h 层有且仅有k个叶结点,前 h-1 层满
-
求总结点数:
前 h-1 层有 2 h − 1 − 1 2^{h-1}-1 2h−1−1 个结点,故共有 2 h − 1 − 1 + k 2^{h-1}-1+k 2h−1−1+k 个结点
-
求总叶结点数:
第 h-1 层有叶子结点的结点数为 ⌈ k 2 ⌉ \lceil \frac{k}{2} \rceil ⌈2k⌉ ,故第 h-1 层有 2 h − 2 − ⌈ k 2 ⌉ 2^{h-2}-\lceil \frac{k}{2} \rceil 2h−2−⌈2k⌉ 个叶结点,故共有 2 h − 2 − ⌈ k 2 ⌉ + k = 2 h − 2 + ⌈ k 2 ⌉ 2^{h-2}-\lceil \frac{k}{2} \rceil + k=2^{h-2}+\lceil \frac{k}{2} \rceil 2h−2−⌈2k⌉+k=2h−2+⌈2k⌉ 个叶结点
-
-
3.2.3 存储结构
-
顺序存储
自上而下,自左向右依次存入数组,最多占 2 h − 1 2^h-1 2h−1 个连续存储单元
适用于 满二叉树 和 完全二叉树
-
链式存储
数据域+左指针域+右指针域。
但 n 个结点含有 n+1 个空指针域
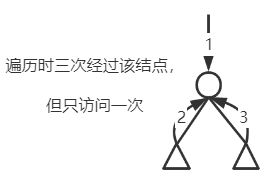
3.2.4 二叉树的遍历
按某条搜索路径,使树中每个结点都被访问一次
- 二叉树结点 ⟶ 映射 \stackrel{映射}{\longrightarrow} ⟶映射线性队列
1. 递归框架
| 先序NLR | 中序LNR | 后序LRN |
|---|---|---|
| visit(T); | InOrder(T->lchild); | PostOrder(T->lchild); |
| PreOrder(T->lchild); | visit(T); | PostOrder(T->rchild); |
| PreOrder(T->rchild); | InOrder(T->rchild); | visit(T); |
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 树高 ) O(树高) O(树高) 最坏 O ( n ) O(n) O(n)
注
2. 非递归遍历
中序
- 沿当前结点的左孩子依次入栈,直至为
NULL pop一次,访问栈顶元素p,并检查其右孩子p.rchild- 若为
NULL,则继续执行 2 - 若不为
NULL,对其右孩子p.rchild执行 1
- 若为
InOrder(T){
p = T;
InitStack(S);
while(p || !IsEmpty(S)){
if(p){
Push(S,p);
p = p->lchild;
}else{
Pop(S,p);
visit(p);
p = p->rchild;
}
}
}
先序
- 访问当前结点,沿左孩子入栈,直至
NULL - 栈顶元素
p出栈,检查其右孩子p.rchild- 若为
NULL,继续执行 2 - 若不为
NULL,则执行 1
- 若为
PreOrder(T){
p = T;
InitStack(S);
while(p || !IsEmpty(S)){
if(p){
visit(p);
Push(S,p);
p = p->lchild;
}else{
Pop(S,p);
p = p->rchild;
}
}
}
后序
- 沿当前结点的左孩子入栈,至
NULL - 读栈顶元素
p- 若其右孩子
p.rchild不为NULL,且未被访问,则执行 1 - 若其右孩子为空,则弹出栈顶元素,并访问该元素,继续执行 2
- 若其右孩子
注
-
左子树全入栈后,还需要对右子树进行相同操作
-
栈顶元素出栈,要么其右孩子为
NULL,要么已经访问完该结点的所有子树-
必须分清是从左子树返回该元素还是从右子树返回该元素
增设辅助指针
pre,记录最近访问的结点,若pre == p->rchild表示已经访问完全部子树
-
PostOrder(T){
p = T;
pre = NULL;
while(p || !IsEmpty(S)){
if(p){//走到最左子树最右结点
Push(S,p);
p = p->lchild;
}else{
GetTop(S,p);//获取栈顶元素
if(p->rchild && p->rchild!=pre)
p = p->rchild;//右子树存在且未被访问
else{
Pop(S,p);
visit(p->data);//访问根结点
pre=p;//记录最近访问过的结点
p=NULL;//结点访问完后重置
}
}
}
}
3. 层序遍历
-
根入队
-
出队,访问该结点
-
有左孩子,将左孩子入队
-
有右孩子,将右孩子入队
-
-
返回 1 直至队空
SeqOrder(T){
InitQueue(Q);
EnQueue(T);
while(!IsEmpty(Q)){
TNode p = DeQueue(Q);
visit(p);
if(p->lchild)
EnQueue(p->lchild);
if(p->rchild)
EnQueue(p->rchild);
}
}
4. 遍历总结
遍历序列->二叉树
只要有中序序列,一定可以唯一确定一棵二叉树
- 先序与中序遍历,相当于以先序入栈,中序出栈。不同的出栈序列对应不同的二叉树
先序与后序相等
由题设 NLR==LRN ,故当 L&R==∅ 时,才成立
- 只有根结点
先序与后序相反
由题设 NLR==LRN ,故当 L==NULL 或 R==NULL 可得到先序与后序序列相反
3.2.5 线索二叉树
线索二叉树为一种 物理结构 :加上线索的链表结构
1. 原理
-
二叉树遍历实质上是将二叉树结点排列为 线性序列
除首尾结点,都有一个直接前驱和直接后继
-
二叉树中有
n+1个空指针
2. 规则
-
无左孩子,
lchild->前驱结点 -
无右孩子,
rchild->后继结点 -
tag域,0表示孩子结点,1表示线索
存储结构:线索链表
线索:指针
线索化:将二叉链表中的空指针改为线索
3. 中序线索二叉树代码
结点定义
typedef struct BiThrNode{
ElemType data;
struct BiThrNode *Lchild,*Rchild;
PointerTag Ltag,Rtag;
}*BiThrTree;
建立中序二叉线索树
void InOrderThreading(BiThrTree &Thrt,BiThrTree root){
if(!Thrt=(BiThrTree)malloc(sizeof(BiThrNode)))
exit(OVERFLOW);//Thrt指向中序线索化链表的头结点
Thrt->Rtag = Thread;//线索树的右指针域指向线索数的根结点
Thrt->Rchild = Thrt;
if(!root)//若该树为空树,则左右孩子为线索,分别指向根
Thrt->Lchild = Thrt;
else{
Thrt->Ltag = Link;//线索树的前驱指向二叉树的根结点
Thrt->Lchild = root;
pre = Thrt;
InThreading(root);//中序遍历进行中序线索化
pre->Rchild = Thrt;//最后一个结点的右指针域指向线索树根结点
pre->Rtag = Thread;
Thrt->Rchild = pre;
}
}
void InThreading(BiThrTree p){
if(p){
InThreading(p->Lchild);//左子树线索化
if(!p->Lchild) //前驱线索
p->Ltag = Thread,p->Lchild = pre;
if(!p->Rchild) //后继线索
pre->Rtag = Thred; pre->Rchild = p;
pre = p;
InThreading(p->Rchild);//右子树线索化
}
}
中序线索二叉树找指定结点后继
BiThrTree InorderNext(BiThrTree p){
if(p->Rtag == Link)//有左孩子,则直接后继为右孩子
return p->Rchild;
else{//找右子树的最左结点
q = p->Rchild;
while(q->Ltag==Thread)
q = q->Lchild;
return q;
}
}
4. 先&后序线索二叉树
构造
修改调用线索化递归函数的位置
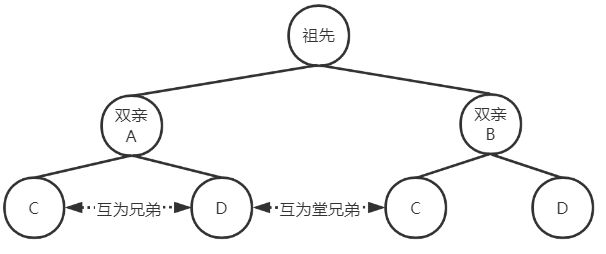
先序找后继
有左孩子,左孩子为后继;无左孩子但有右孩子,则右孩子为后继
若是叶子结点,则其右亲兄弟或最左堂兄弟为其后继
后序找后继
-
若
p为二叉树根,则其后继为空 -
若
p为其双亲的右孩子,或为双亲无右孩子的左孩子,则后继为其双亲结点 -
若
p为其双亲的左孩子,且其双亲有右孩子,则后继为其双亲的最左右子结点
后序线索二叉树不能有效解决后序找后继的问题
- 从右孩子返回父节点,但右孩子的右指针域不一定是线索,故使用三叉链表,增设
parent域- 而 先序线索二叉树与后序线索二叉树 可遍历整棵树
typedef struct BiThrNode{
ElemType data;
struct BiThrNode *Lchild,*Rchild,*parent;//三叉链表
PointerTag Ltag,Rtag;
}
BiThrTree PostOrderNext(BiThrTree p){
if(p->Rtag == Link)
return p->Rchild;
else{
//查找p所指结点的父节点
if(p == p->parent->Rchild) return p->parent;
if(p == p->parent->Lchild && p->parent->Rtag == Thread)
return p->parent;
//查找双亲结点的右子树最左结点
q = p->parent->Rchild;
while(q->Ltag == Link || q->Rtag == Link){
if(q->Ltag == Link)//左子结点优先级高
q = q->Lchild;
else
q = q->Rchild;
}
}
}
3.2.6 二叉树的应用
1. 二叉排序树
typedef struct TreeNode{
ElementType key;
struct TreeNode *parent,*left,*right;
}Node, *BST;
p->lchild->data < p->data < p->rchild->data;
- 中序遍历可以得到有序序列
查找
while(!T && key != T->data){
if(key < T->data)
T = T->lchild;
else
T = T->rchild;
}
一棵二叉排序树上的查找序列,第 n,n+1 个数不能分居第 n-1 个数的两侧如
BST插入
查找过程中,不存在目标结点,再插入
新插入的结点一定是一个叶结点,且是查找失败时,查找路径上访问的最后一个结点的孩子
void Insert(BST T,Node *p){
Node *x = T;
Node *y = NULL;
while(x != NULL){//查找目标结点
y = x;
if(x->key > p->key)
x = x->left;
else
x = x->right;
}
p->parent = y;
if(y == NULL)//第一个结点
T = p;
else if(y->key > p->key)//待插入结点值小于叶结点
y->left = p;
else//待插入结点值大于等于叶结点
y->right = p;
}
BST删除
BST中元素间的相对位置与BST中序序列中元素间的相对位置相同
- 若删除结点
p是叶结点,则直接删除 - 若删除结点
p是某单支树,则用其孩子结点代替 - 若删除结点
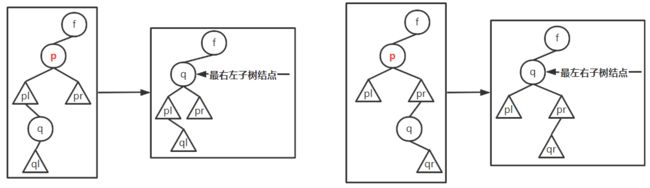
p有左右孩子- 用直接后继
next代替,p的左孩子变为next的左孩子,p的右孩子变为next的最右左子树 - 用直接前驱
pre代替,p的右孩子变为pre的右孩子,p的左孩子变为pre的最左右子树
- 用直接后继
void Transplant(BST T, Node *x, Node *y){// y替换x的位置
if(x->parent == NULL)
T = y;
else if(x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
if(y != NULL)
y->parent = x->parent;
}
void Delete(BST T, Node *p){
if(p->left == NULL)//p左子树空,则用其右孩子根结点代替p的位置
Transplant(T, p, p->right);
else if(p->right == NULL)//p的右子树为空,用其左孩子代替p的位置
Transplant(T, p, p->left);
else{//按上图第二种情况写,第一种类推
Node *q = FindMin(p->right); //找p的最左右子树结点
if (q->parent != p){
Transplant(T, q, q->right);
q->right = p->right;
q->right->parent = q;
}
Transplant(T, p, q);
q->left = p->left;
q->left->parent = q;
}
}
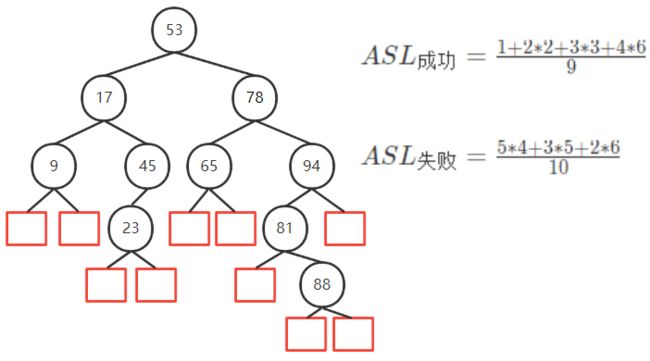
BST平均查找长度
计算
- 查找失败的情况相当于将 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 用n个数分为 n+1 个区间
最好情况 ASL = O ( l o g n ) O(log_n) O(logn) 平衡二叉树
最坏情况 ASL = O ( n ) O(n) O(n) 单链表
二分查找与二叉排序树
-
ASL相同
-
二分查找判定树唯一
-
BST是动态树,不唯一
插入顺序不同,生成的BST不同
-
-
区别
类型 存储结构 构建时间复杂度 二分查找 静态查找表 有序顺序表 O ( n ) O(n) O(n) BST 动态查找表 修改指针 O ( l o g 2 n ) O(log_2n) O(log2n)
2. 平衡二叉树
平衡因子: h L − h R h_L-h_R hL−hR
平衡二叉树:
- 左右子树都是平衡二叉树
- ∣ h L − h R ∣ ≤ 1 |h_L-h_R| \le 1 ∣hL−hR∣≤1
平衡二叉树的插入
操作对象:最小不平衡子树
- 距插入点最近的 平衡因子的绝对值为2 的子树
-
调整前,新插入的结点一定是叶结点
-
从下向上调整
-
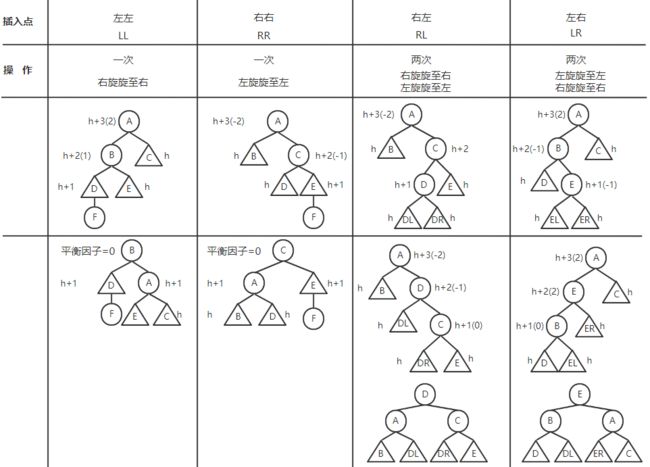
不平衡点位置字母相同,则旋转一次;不平衡点位置字母不同,则旋转两次
LL / RR :旋转一次
LR / RL:旋转两次
-
字母不同,则逆向旋转;字母相同,则同向旋转
LL,则右旋;RR则左旋
RL,则先右旋再左旋;LR,则先左旋再右旋
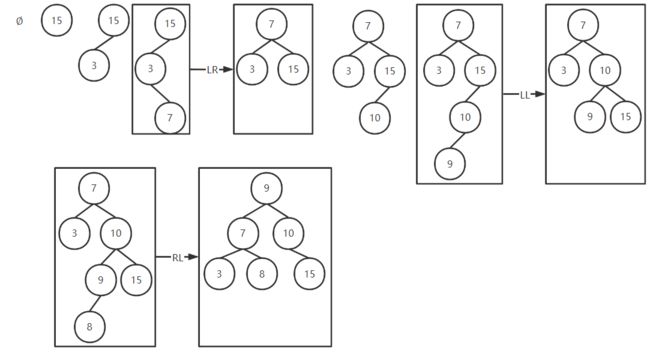
举例 :{ 8 , 3 ,7 ,10 ,9 ,15 , 8 }
平衡二叉树查找
-
ASL: O ( l o g 2 n ) O(log_2n) O(log2n)
-
比较次数不超过平衡二叉树树的深度,最大深度 h = l o g ϕ 5 ( n + 1 ) − 2 h=log_\phi\sqrt5(n+1)-2 h=logϕ5(n+1)−2,其中 ϕ = 1 + 5 2 \phi=\frac{1+\sqrt5}{2} ϕ=21+5
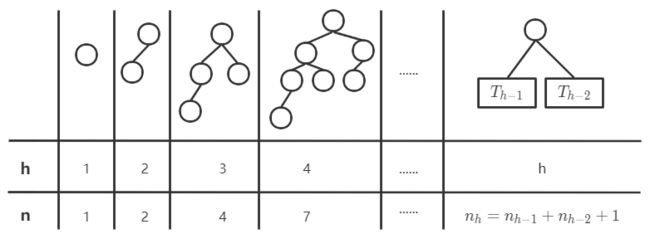
深度为 h h h 的平衡树有最少结点
-
非叶结点平衡因子为1,结点与树高之间的关系: n h = n h − 1 + n h − 2 + 1 n_h=n_{h-1}+n_{h-2}+1 nh=nh−1+nh−2+1
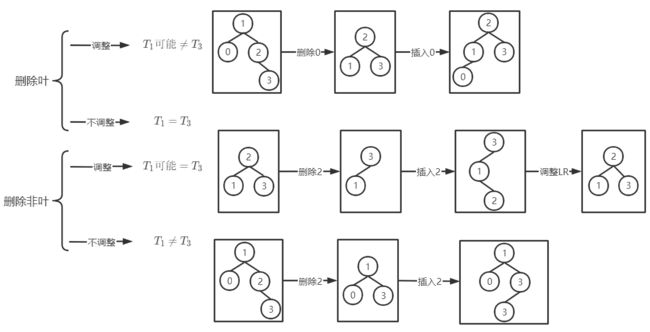
删除后插入
T 1 ⟶ 删除 T 2 ⟶ 插入 T 3 T_1 \stackrel{删除}{\longrightarrow} T_2 \stackrel{插入}{\longrightarrow}T_3 T1⟶删除T2⟶插入T3
3. 哈弗曼树
定义
最优二叉树,其WPL最小
带权路径长度 W P L = ∑ i = 1 n W i ( 结点权值 ) ∗ L i ( 从根到叶结点路径长度 ) 带权路径长度WPL=\sum_{i=1}^{n}W_i(结点权值)*L_i(从根到叶结点路径长度) 带权路径长度WPL=i=1∑nWi(结点权值)∗Li(从根到叶结点路径长度)
原理
一棵 H u f f m a n 树只有度为 0 和 m 的结点 , 由树的结点数与边数的关系 n m + n 0 = m n m + 1. 故 n m = ⌈ n 0 − 1 m − 1 ⌉ 。所以总结点数已知,可以用顺序存储结构 . \begin{aligned} &一棵Huffman树只有度为0和m的结点,由树的结点数与边数的关系n_m+n_0=mn_m+1.\\ &故n_m=\lceil \frac{n_0-1}{m-1}\rceil。所以总结点数已知,可以用顺序存储结构. \end{aligned} 一棵Huffman树只有度为0和m的结点,由树的结点数与边数的关系nm+n0=mnm+1.故nm=⌈m−1n0−1⌉。所以总结点数已知,可以用顺序存储结构.
结点定义
typedef struct{
char ch;
unsigned int weight;
unsigned int parent,lchild,rchild;
}HTNode,*HummanTree;
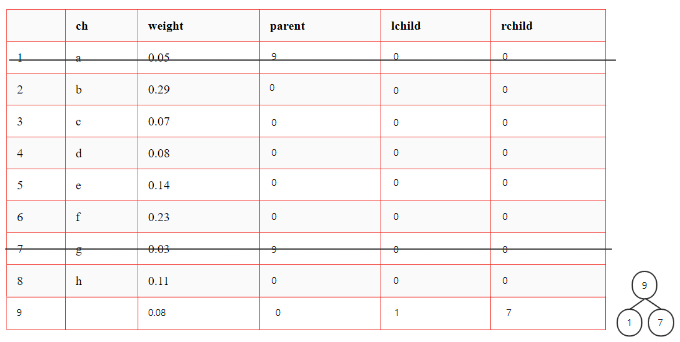
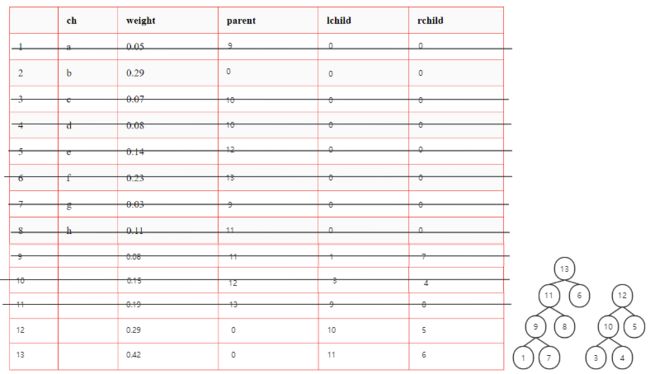
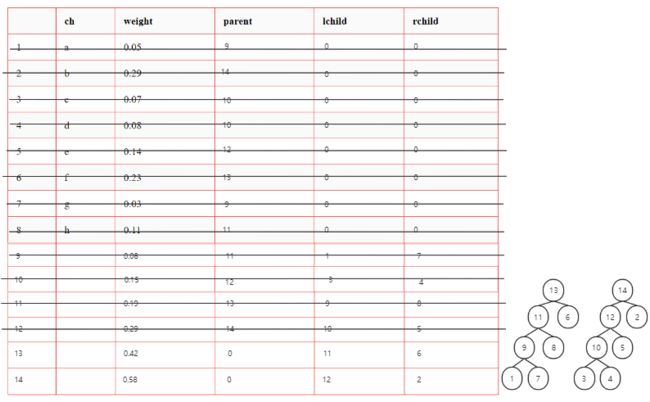
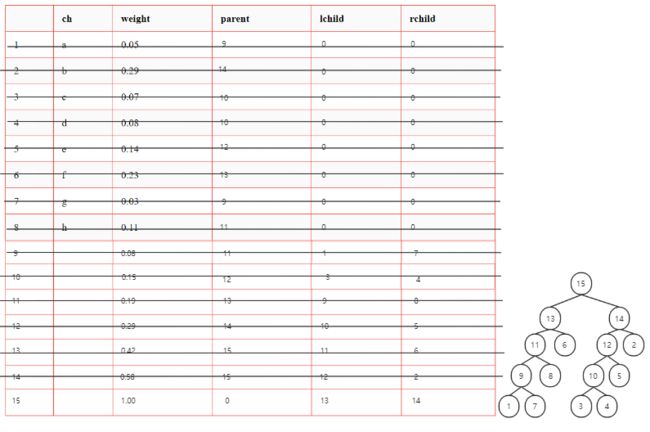
构造哈弗曼树
-
带权结点构成森林F
-
从F中选择权最小的两个结点,求和形成新结点
-
删除原先的两个结点,将新结点加入F
-
反复执行 1. 直至F中只有一棵树
初始状态
| ch | weight | parent | lchild | rchild | |
|---|---|---|---|---|---|
| 1 | a | 0.05 | 0 | 0 | 0 |
| 2 | b | 0.29 | 0 | 0 | 0 |
| 3 | c | 0.07 | 0 | 0 | 0 |
| 4 | d | 0.08 | 0 | 0 | 0 |
| 5 | e | 0.14 | 0 | 0 | 0 |
| 6 | f | 0.23 | 0 | 0 | 0 |
| 7 | g | 0.03 | 0 | 0 | 0 |
| 8 | h | 0.11 | 0 | 0 | 0 |
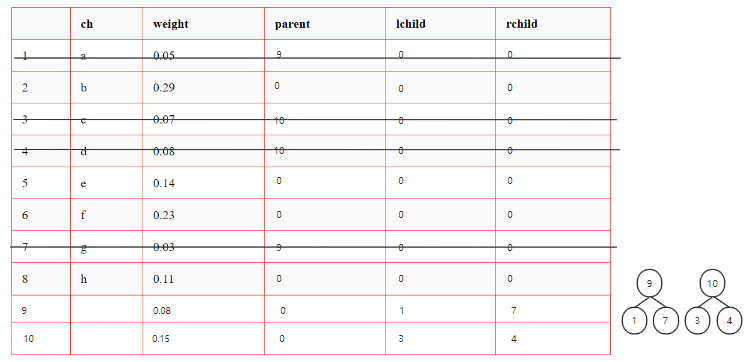
1.
2.
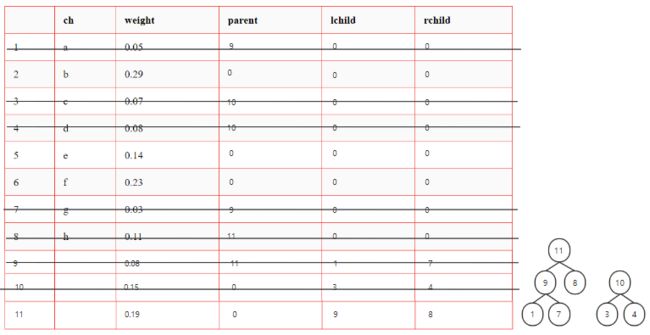
3.
4.
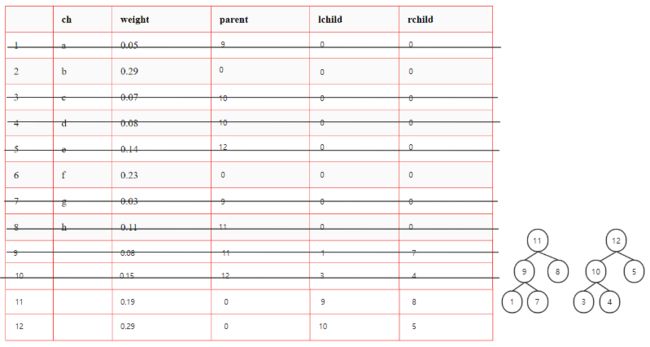
5.
6.
7.
二叉哈夫曼树特点
-
所有初始结点都是叶结点
结点权值越小,到根结点的路径长度越长
-
不存在度为1的结点,在二叉树中 n 2 = n 0 − 1 n_2=n_0-1 n2=n0−1,故哈弗曼树有 2 n 0 − 1 2n_0-1 2n0−1 个结点,新建 n 0 − 1 个结点 n_0-1个结点 n0−1个结点
-
任一非叶结点权值不小于下一层任意节点权
-
二叉树为有序树 ,WPL唯一
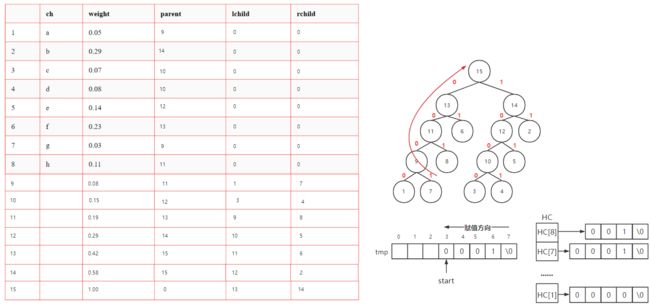
Huffman编码
高频短编码;低频长编码
- Huffman编码是数据压缩码
- 前缀码:没有一个编码是另一个编码的前缀
typedef struct{
char ch;
unsigned int weight;
unsigned int parent,lchild,rchild;
}HTNode,*HummanTree;
HuffmanTree HT;
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC
,int *w,int n_0){
//w存放个字符的权值,构造哈弗曼树,并求出字符的编码
if(n_0 == 1)//只有一个结点
return ;
/* 初始化 */
int n = 2*n_0-1;//总结点数
HT = new HTNode[n+1];
//初始化Huffman存储结构
for(int i = 1;i <= n;++i){
HT[i].weight = w[i-1];
HT[i].parent = 0;
HT[i].lchild = HT[i].rchild = 0;
}
//共需2n_0-1个存储单元
for(;i <= m;i++){
HT[i].parent = 0;
HT[i].lchild = HT[i].rchild = 0;
}
/* 构造哈夫曼树 */
int s1,s2;
for(i=n_0+1;i <= m;i++)0{
//从H[1...i-1]中选择parent为0且weight最小的两结点
//其序号为s1,s2
select(HT,i-1,s1,s2);
HT[s1].parent = i; HT[s2]
HT[i].weight = HT[s1].weight+HT[s2].weight;
}
//从叶到根求每个字符的哈夫曼编码
HC = new char*[n_0+1];
//(char **)malloc((n+1)*sizeof(char *))
tmp = new char[n_0];//树高不会超过n_0,故长度最大为n_0
tmp[n_0-1]='\0';
for(i=1;i <= n_0;++i){
start = n_0-1;//start标记编码的起始坐标
for(c=i,f=HT[i];f!=0;c=f,f=HT[f].parent){
if(HT[f].lchild == c)
tmp[--start]='0';//从叶到根,所以是逆序
else
tmp[--start]='1';
}
HC[i] = new char[n_0-start];
strcpy(HC[i],&tmp[start]);
}
delete tmp[];
3.2.7 红黑树
二叉排序树优势
使用数组,搜索比较方便,但插入删除元素比较麻烦
使用链表,插入和删除元素比较方便,但查找很慢
二叉排序树是数组和链表的折中,适用于动态查找大批量数据
平衡二叉树/红黑树是为了将查找的时间复杂度控制在 $O(logN) $ (即树高)的时间复杂度如果输入集合有限,则使用哈希表;如果输入的集合不确定,则使用平衡二叉树/红黑树
定义
红黑树是为了解决平衡二叉树过于苛刻的要求造成的频繁调整
AVL: − 1 ≤ h e i g h t 左 − h e i g h t 右 ≤ 1 -1\le height_左-height_右 \le 1 −1≤height左−height右≤1
红黑树: 1 2 ≤ h e i g h t 左 h e i g h t 右 ≤ 2 \frac{1}{2} \le \frac{height_左}{height_右}\le 2 21≤height右height左≤2 左右两棵子树树高差不超过一倍
设计思路
// 红黑树的结点定义
struct RBnode{
int key; // 关键字的值
RBnode *parent; // 父节点的指针
RBnode *lChild; // 左孩子的指针
RBnoce *rChild; // 右孩子的指针
int color; // 结点颜色,如可用 0/1 表示 黑/红。也可用枚举型 enum 表示颜色。
};
假设一棵平衡二叉树,结点全是黑。左子树不变,右子树每两层黑结点中间加一个红结点,则左右子树高度差不会超过1倍
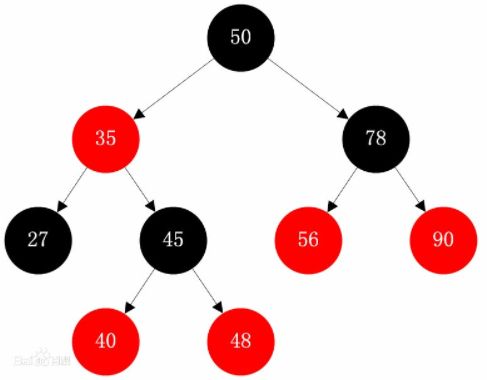
性质
- 结点非黑即红
- 根为黑
- 空结点为叶子,叶子为黑
- 红结点孩子与父亲必为黑
- 从根到任意叶子,经过的黑结点树相等
操作
调色:红黑树引进的操作
调位:AVL
调色
新加的结点都是红结点
叶黑根黑
不红红,可黑黑
如果新加结点的父节点和叔叔结点都是红,则将 原来的 父节点与叔叔结点变为黑结点,其祖父结点变为红结点
- 如果祖父结点的父节点是黑结点,则不做别的操作
- 如果祖父结点的父节点是红结点,则按照红黑树的规则向根结点调整
调色要保证一整层都要调,若一层中有不一样的颜色,只能调位
调位
新加节点是红,如果父节点是红结点,叔叔结点是黑
AVL的调位方法,要满足 红结点的孩子与父亲都是黑结点 ,适当调色
插入
从一个空的红黑树开始,插入:20,10,5,30,40,57,3,2,4,35,25,18,22,23,24,19,18
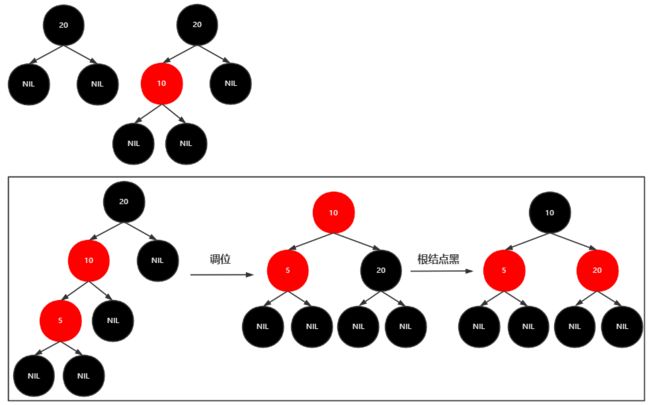
插入20,10,5
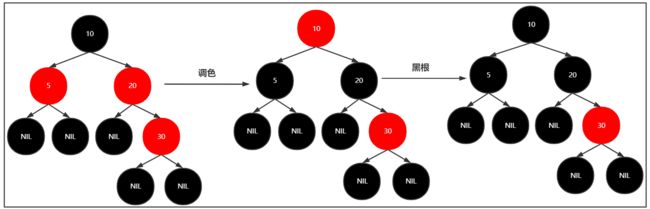
插入30
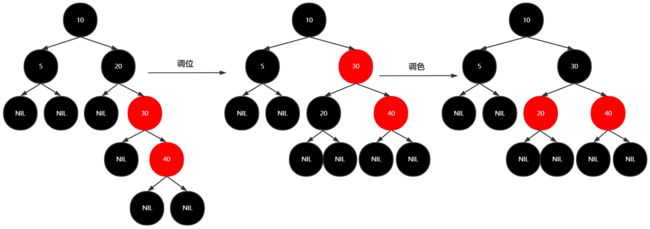
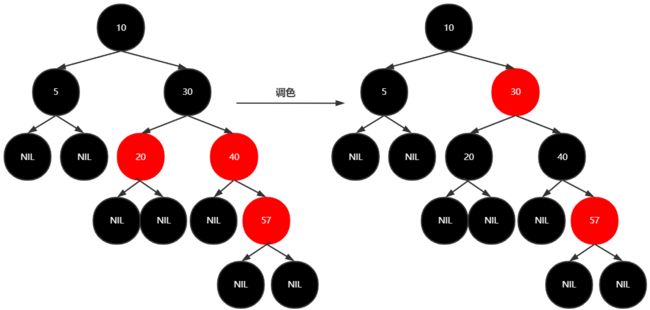
插入40
插入57
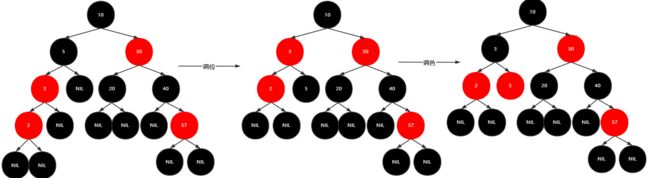
插入3,2
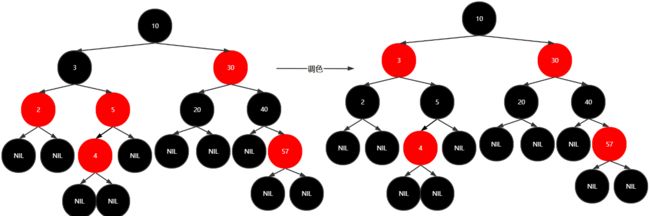
插入4
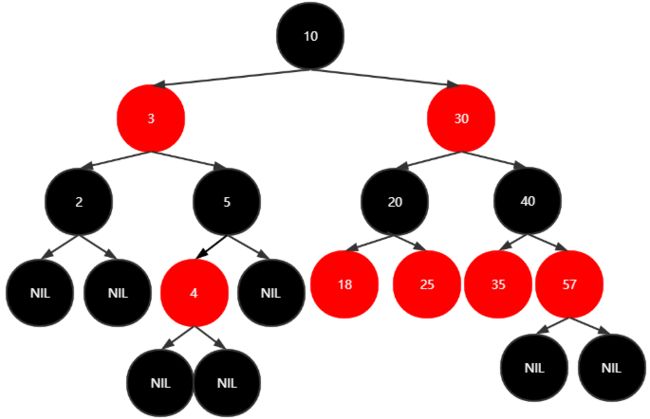
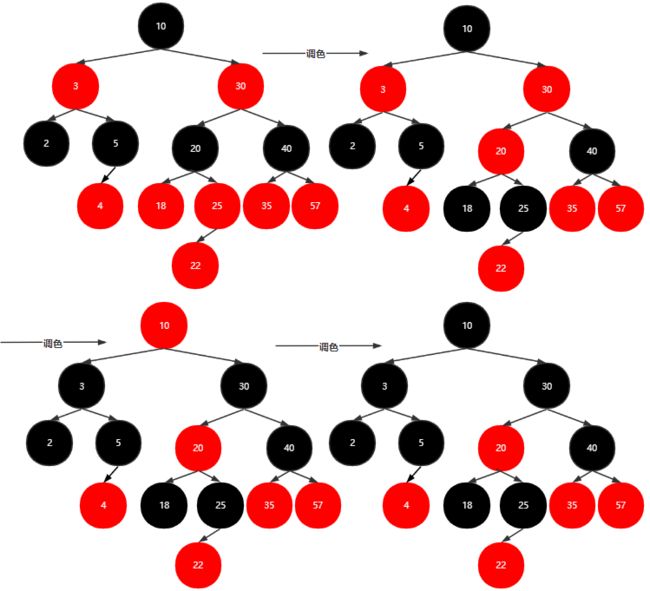
插入35,25,18
插入22
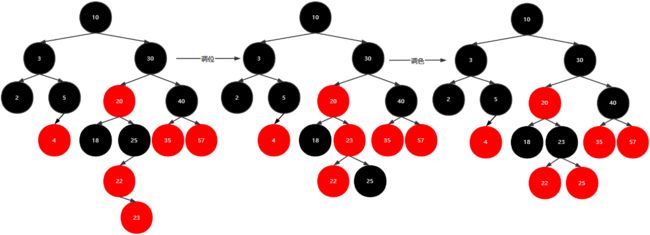
插入23
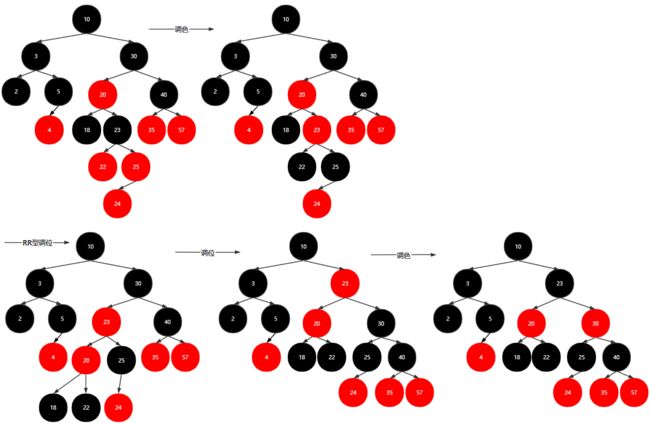
插入24