机器学习模型身后的数学和统计背景:统计与信息论Probability and Information Theory
术语
样本空间(sample space): Ω \Omega Ω,包含了所有可能出现的结果的集合。比如在掷一次骰子的样本空间可以用{1,2,3,4,5,6}表示。
事件集(event space): F F F,a collection of subsets of Ω \Omega Ω,用来表示出现的结果。事件集未必是样本空间中的单一元素,也可以是复杂元素。比如在掷一次骰子的样本空间中,可以用{1,3,5}表示结果为奇数的事件。
概率函数(probability function): P P P,该函数完成了从事件到该事件发生概率的映射。
概率法则
贝叶斯
A的先验概率(prior probability of A): P(A)
A的后验概率(posterior probability of an event A given B): P(A|B)
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac {P(B|A)P(A)} {P(B)} P(A∣B)=P(B)P(B∣A)P(A)
独立事件
事件 A 1 , A 2 , . . . , A n A_1, A_2,\ ...\ , A_n A1,A2, ... ,An相互独立,当且仅当该事件集合的所有子集满足条件 P ( A i 1 , A i 2 , . . . , A i k ) = ∏ j = 1 k P ( A i j ) P(A_{i1}, A_{i2},\ ...\ , A_{ik}) = \prod_{j=1}^k P(A_{ij}) P(Ai1,Ai2, ... ,Aik)=∏j=1kP(Aij)
随机变量
一般来说,我们使用大写字母表示随机变量本身,用对应的小写字母代表该变量的取值。
可以从CDF分辨一个随机变量是离散变量、连续变量、抑或是两者都不是。
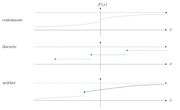
离散变量
满足条件 P ( X ∈ X ) = 1 P(X \in \mathcal X) = 1 P(X∈X)=1 for some countable set X ⊂ R \mathcal X \sub R X⊂R。
离散变量可以被其概率质量函数充分说明。
概率质量函数
probability mass function (pmf)。定义 p ( x ) = P ( X = x ) ∀ x ∈ X p(x) = P(X=x) \ \forall \ x \in X p(x)=P(X=x) ∀ x∈X。
性质:
- p ( x ) ≥ 0 p(x) \ge 0 p(x)≥0
- ∑ x ∈ X p ( x ) = 1 \sum_{x \in X} p(x) = 1 ∑x∈Xp(x)=1
我们常用记号 X ∼ p ( x ) X \sim p(x) X∼p(x)来表示X的pmf是p(x)。
累积分布函数
cumulative density function (cdf)。定义 F ( x ) = P ( X ≤ x ) F(x) = P(X \le x) F(x)=P(X≤x)。
性质
-
F ( x ) ≥ 0 F(x) \ge 0 F(x)≥0,且单调非递减
-
l i m x − > ∞ F ( x ) = 1 lim_{x->\infty} F(x) = 1 limx−>∞F(x)=1, l i m x − > − ∞ F ( x ) = 0 lim_{x->-\infty} F(x) = 0 limx−>−∞F(x)=0
-
F ( x ) F(x) F(x) 是右连续的,即 l i m x − > a + F ( x ) = F ( a ) lim_{x->a^+} F(x) = F(a) limx−>a+F(x)=F(a)
-
P ( X = a ) = F ( a ) − l i m x − > a − F ( a ) P(X=a) = F(a) \ - \ lim_{x->a^-} F(a) P(X=a)=F(a) − limx−>a−F(a)
经典的离散变量
Bernoulli
p ( x ) = p x + ( 1 − p ) ( 1 − x ) ; x ∈ { 0 , 1 } p(x) = px + (1-p)(1-x); \ x \in \{0,1\} p(x)=px+(1−p)(1−x); x∈{0,1}
应用场景为投篮投进的概率。
v a r ( X ) = p ( 1 − p ) var(X) = p(1-p) var(X)=p(1−p)
Geometric
p ( x ) = p ( 1 − p ) x p(x) = p(1-p)^x p(x)=p(1−p)x
应用场景为抛硬币直到看到一次正面朝上的概率。
Binomial
p ( x ) = C ( n , k ) ∗ p k ( 1 − p ) n − k p(x) = C(n, k)*p^k(1-p)^{n-k} p(x)=C(n,k)∗pk(1−p)n−k
应用场景为连续抛n次硬币看到k次正面朝上的概率。
Poisson
p ( x ) = λ x x ! e − λ ; λ > 0 p(x) = \frac {\lambda^x} {x!} e^{-\lambda}; \lambda > 0 p(x)=x!λxe−λ;λ>0
应用场景为在给定时间段内事件的数量。
Categorical
可以自己根据场景定义pmf。
连续变量
概率密度函数
probability density function (pdf)。定义 f ( x ) = d F ( x ) d x f(x) = \frac {dF(x)} {dx} f(x)=dxdF(x)。
性质
- f ( x ) ≥ 0 f(x) \ge 0 f(x)≥0
- ∫ − ∞ ∞ f ( x ) d x = 1 \int_{-\infty}^{\infty} f(x) dx = 1 ∫−∞∞f(x)dx=1,同理 P ( X ≤ a ) = ∫ − ∞ a f ( x ) d x P(X \le a) = \int_{-\infty}^{a} f(x) dx P(X≤a)=∫−∞af(x)dx
- P ( X ∈ A ) = ∫ x ∈ A f ( x ) d x P(X \in A) = \int_{x \in A} f(x) dx P(X∈A)=∫x∈Af(x)dx
我们常用记号 X ∼ f ( x ) X \sim f(x) X∼f(x)来表示 X X X的pdf是 f ( x ) f(x) f(x)。
累积分布函数
与离散变量的CDF部分相同。
经典的连续变量
高斯Gaussian
X ∼ N ( μ , σ 2 ) X \sim \mathcal N(\mu, \sigma^2) X∼N(μ,σ2)
f ( x ) = 1 2 π σ 2 ∗ e − ( x − μ ) 2 2 σ 2 f(x) = \frac {1} {\sqrt{2\pi \sigma^2}} * e^{-\frac {(x-\mu)^2} { 2\sigma^{2}}} f(x)=2πσ21∗e−2σ2(x−μ)2
Logistic
X ∼ l o g i s t i c ( μ = 0 , s = 0 ) X \sim logistic(\mu=0, s=0) X∼logistic(μ=0,s=0)
f ( x ) = e − x ( 1 + e − x ) 2 f(x) = \frac {e^{-x}} {(1+e^{-x})^2} f(x)=(1+e−x)2e−x
Uniform
X ∼ U [ a , b ] X \sim U[a,b] X∼U[a,b]
f ( x ) = 1 b − a ; f o r a ≤ x ≤ b f(x) = \frac 1 {b-a}; \ for \ a \le \ x \le b f(x)=b−a1; for a≤ x≤b
v a r ( X ) = ( b − a ) 2 12 var(X) = \frac {(b-a)^2} {12} var(X)=12(b−a)2
Exponential
X ∼ E x p ( λ ) ; λ > 0 X \sim Exp(\lambda); \lambda > 0 X∼Exp(λ);λ>0
f ( x ) = λ e − λ x ; x ≥ 0 f(x) = \lambda e^{-\lambda x}; \ x \ge 0 f(x)=λe−λx; x≥0
Laplace
X ∼ L a p ( μ , b ) ; b > 0 X \sim Lap(\mu, b); \ b > 0 X∼Lap(μ,b); b>0
f ( x ) = 1 2 b e − ∣ x − μ ∣ b f(x) = \frac 1 {2b} e^{-\frac{|x - \mu|} {b}} f(x)=2b1e−b∣x−μ∣
期望&方差&矩
期望
假设 X ∼ p ( x ) X \sim p(x) X∼p(x),则 E [ X ] = ∑ x ∈ X x p ( x ) E[X] = \sum_{x \in X} xp(x) E[X]=∑x∈Xxp(x)。容易得到 E [ g ( X ) ] = ∑ x ∈ X g ( x ) p ( x ) E[g(X)] = \sum_{x \in X} g(x)p(x) E[g(X)]=∑x∈Xg(x)p(x)。
假设 X ∼ f ( x ) X \sim f(x) X∼f(x),则 E [ X ] = ∫ − ∞ ∞ x f ( x ) E[X] = \int_{-\infty}^{\infty} xf(x) E[X]=∫−∞∞xf(x)。容易得到 E [ g ( X ) ] = ∫ − ∞ ∞ g ( x ) f ( x ) d x E[g(X)] = \int_{-\infty}^{\infty} g(x)f(x) dx E[g(X)]=∫−∞∞g(x)f(x)dx。
需要注意的是,期望是有可能发散的。比如 g ( x ) = x − 2 ; x ≥ 1 g(x) = x^{-2}; \ x \ge 1 g(x)=x−2; x≥1的期望就是正无穷。
性质
- 线性, E [ a ∗ g ( X ) + b ∗ h ( X ) + c ] = a ∗ E [ g ( X ) ] + b ∗ E [ h ( X ) ] + c E[a*g(X) + b*h(X) + c] = a*E[g(X)] + b*E[h(X)] + c E[a∗g(X)+b∗h(X)+c]=a∗E[g(X)]+b∗E[h(X)]+c
- 可转换性,如果 Y = g ( X ) Y = g(X) Y=g(X),那么 E [ Y ] = E [ g ( X ) ] E[Y] = E[g(X)] E[Y]=E[g(X)]
方差
方差 v a r ( X ) var(X) var(X),有时候也用 D ( X ) D(X) D(X)表示。
D [ X ] = E [ ( X − E [ X ] ) 2 ] = E [ X 2 ] − ( E [ X ] ) 2 D[X] = E[(X - E[X])^2] = E[X^2] - (E[X])^2 D[X]=E[(X−E[X])2]=E[X2]−(E[X])2。数学推导见下,
D [ X ] = ∑ i = 1 n ( x i − μ ) 2 p i = ∑ i = 1 n x i 2 p i − 2 μ ∑ i = 1 n x i p i + μ 2 ∑ i = 1 n p i = ∑ i = 1 n x i 2 p i − 2 μ 2 + μ 2 ∑ i = 1 n p i = ∑ i = 1 n x i 2 p i − μ 2 = E [ X 2 ] − ( E [ X ] ) 2 D[X] = \sum_{i=1}^n (x_i - \mu)^2 p_i \\\\ = \sum_{i=1}^n x_i^2 p_i - 2\mu \sum_{i=1}^n x_i p_i + \mu^2 \sum_{i=1}^n p_i \\\\ = \sum_{i=1}^n x_i^2 p_i - 2 \mu^2 + \mu^2 \sum_{i=1}^n p_i \\\\ = \sum_{i=1}^n x_i^2 p_i - \mu^2 \\\\ = E[X^2] - (E[X])^2 D[X]=i=1∑n(xi−μ)2pi=i=1∑nxi2pi−2μi=1∑nxipi+μ2i=1∑npi=i=1∑nxi2pi−2μ2+μ2i=1∑npi=i=1∑nxi2pi−μ2=E[X2]−(E[X])2
性质
- D [ a x + b ] = a 2 ∗ D ( x ) D[ax+b] = a^2*D(x) D[ax+b]=a2∗D(x)
矩
英文是moment,有时候被称为动差。
i i i阶矩被定义为 E [ X i ] E[X^i] E[Xi],可以发现一阶矩正好就是期望。0阶矩被定义为1。
联合概率
假设iid, p ( x , y ) = P ( X = x , Y = y ) p(x, y) = P(X=x, Y=y) p(x,y)=P(X=x,Y=y), ( X , Y ) ∼ p ( x , y ) (X,Y) \sim p(x,y) (X,Y)∼p(x,y)。
联合概率质量函数
边缘分布(marginals)可以表示成 p ( x ) = ∑ y ∈ Y p ( x , y ) p(x) = \sum_{y \in \mathcal Y} p(x, y) p(x)=∑y∈Yp(x,y)
X X X, Y Y Y相互独立<=> p ( x , y ) = p ( x ) p ( y ) ∀ x ∈ X , y ∈ Y p(x, y) = p(x)p(y) \ \forall \ x \in \mathcal X, y \in \mathcal Y p(x,y)=p(x)p(y) ∀ x∈X,y∈Y
联合累积分布函数
F ( x , y ) = P ( X ≤ x , Y ≤ y ) ∀ x ∈ R , y ∈ R F(x,y) = P(X \le x, Y \le y) \ \forall \ x \in R, y \in R F(x,y)=P(X≤x,Y≤y) ∀ x∈R,y∈R
容易得到 P ( a < X ≤ b , c < Y ≤ d ) = F ( b , d ) − F ( a , d ) − F ( b , c ) + F ( a , c ) P(a < X \le b, c < Y \le d) = F(b,d) - F(a,d) - F(b,c) + F(a,c) P(a<X≤b,c<Y≤d)=F(b,d)−F(a,d)−F(b,c)+F(a,c)。
性质
- 在x和y方向均不递减
- l i m x − > + ∞ F ( x , y ) = F ( y ) lim_{x->+\infty} F(x,y) = F(y) limx−>+∞F(x,y)=F(y)
联合概率密度函数
f ( x , y ) = ∂ 2 F ( x , y ) ∂ x ∂ y f(x,y) = \frac {\partial^2 F(x,y)} {\partial x \partial y} f(x,y)=∂x∂y∂2F(x,y)
计算 X X X的边缘联合概率质量函数(marginal pdf): f ( x ) = ∫ − ∞ ∞ f ( x , y ) d y f(x) = \int_{-\infty}^{\infty} f(x,y) dy f(x)=∫−∞∞f(x,y)dy
性质
- P ( ( X , Y ) ∈ A ) = ∫ ( x , y ) ∈ A f ( x , y ) d x d y P((X,Y) \in A) = \int_{(x,y) \in A} f(x,y) dxdy P((X,Y)∈A)=∫(x,y)∈Af(x,y)dxdy
联合高斯
Jointly Gaussian,也被称为Bivariate Gaussian。定义 ρ \rho ρ为关联系数(correlation coefficient)。
变量间的相互关系
协方差
covariance。用于衡量两个随机变量的联合变化程度。
c o v ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E [ Y ] ) ] = E [ X Y ] − E [ X ] E [ Y ] cov(X, Y) = E[(X - E[X])(Y - E[Y])] = E[XY] - E[X]E[Y] cov(X,Y)=E[(X−E[X])(Y−E[Y])]=E[XY]−E[X]E[Y]
如果两个变量相互独立,那么协方差是0。但是反之并不成立!如果两个变量的协方差是0,我们只能说这两个变量不相关,但是不能得出相互独立的结论。

上面这张图就是协方差为0但变量不相互独立的例子。
我们仔细观察可以发现,方差是协方差的一种特殊情况,是变量与自身的协方差。
v a r ( X + Y ) = v a r ( X ) + v a r ( Y ) + 2 c o v ( X , Y ) var(X+Y) = var(X) + var(Y) + 2cov(X,Y) var(X+Y)=var(X)+var(Y)+2cov(X,Y)。
我们可以用方差的公式证明这一推论。
v a r ( X + Y ) = E [ ( X + Y ) 2 ] − ( E [ X + Y ] ) 2 = E [ X 2 ] + E [ Y 2 ] + 2 E [ X Y ] − ( E [ X + Y ] ) 2 = ( E [ X 2 ] − E [ X ] 2 + E [ X ] 2 ) + ( E [ Y 2 ] − E [ Y ] 2 + E [ Y ] 2 ) + 2 E [ X Y ] − ( E [ X + Y ] ) 2 = v a r ( X ) + E [ X ] 2 + v a r ( Y ) + E [ Y ] 2 + 2 E [ X Y ] − ( E [ X + Y ] ) 2 = v a r ( X ) + v a r ( Y ) + E [ X ] 2 + E [ Y ] 2 + 2 E [ X Y ] − ( E [ X ] + E [ Y ] ) 2 = v a r ( X ) + v a r ( Y ) + 2 E [ X Y ] + E [ X ] 2 + E [ Y ] 2 − ( E [ X ] + E [ Y ] ) 2 = v a r ( X ) + v a r ( Y ) + 2 E [ X Y ] − 2 E [ X ] [ Y ] = v a r ( X ) + v a r ( Y ) + 2 c o v ( X , Y ) var(X+Y) = E[(X+Y)^2] - (E[X+Y])^2 \\\\ = E[X^2] + E[Y^2] + 2E[XY] - (E[X+Y])^2 \\\\ = (E[X^2] - E[X]^2 + E[X]^2) + (E[Y^2] - E[Y]^2+ E[Y]^2) + 2E[XY] - (E[X+Y])^2 \\\\ = var(X) + E[X]^2 + var(Y) + E[Y]^2 + 2E[XY] - (E[X+Y])^2 \\\\ = var(X) + var(Y) + E[X]^2 + E[Y]^2 + 2E[XY] - (E[X]+E[Y])^2 \\\\ = var(X) + var(Y) + 2E[XY] + E[X]^2 + E[Y]^2 - (E[X]+E[Y])^2 \\\\ = var(X) + var(Y) + 2E[XY] - 2E[X][Y] \\\\ = var(X) + var(Y) + 2cov(X,Y) var(X+Y)=E[(X+Y)2]−(E[X+Y])2=E[X2]+E[Y2]+2E[XY]−(E[X+Y])2=(E[X2]−E[X]2+E[X]2)+(E[Y2]−E[Y]2+E[Y]2)+2E[XY]−(E[X+Y])2=var(X)+E[X]2+var(Y)+E[Y]2+2E[XY]−(E[X+Y])2=var(X)+var(Y)+E[X]2+E[Y]2+2E[XY]−(E[X]+E[Y])2=var(X)+var(Y)+2E[XY]+E[X]2+E[Y]2−(E[X]+E[Y])2=var(X)+var(Y)+2E[XY]−2E[X][Y]=var(X)+var(Y)+2cov(X,Y)
性质
- 对称性
- c o v ( a X , b Y ) = a b c o v ( X , Y ) cov(aX, bY) = ab \ cov(X,Y) cov(aX,bY)=ab cov(X,Y)
相关
correlation。显示两个随机变量之间线性关系的强度和方向。如果变量之间有很强的关系但不是线性关系,correlation也很可能是0。
E [ X Y ] = ∑ x ∈ X ∑ y ∈ Y x y p ( x , y ) E[XY] = \sum_{x \in X} \sum_{y \in Y} xyp(x,y) E[XY]=∑x∈X∑y∈Yxyp(x,y)

上面图示分别对应correlation值接近0,1,-1.
相关系数
Correlation Coefficient。一般指的都是皮尔森系数。
ρ = c o v ( X , Y ) v a r ( X ) v a r ( Y ) \rho = \frac {cov(X, Y)} {\sqrt{var(X)var(Y)}} ρ=var(X)var(Y)cov(X,Y)
性质
- 对称性
协方差矩阵
一个向量由多个随机变量组成(默认是列向量),用 v v v或者 x x x表示。
随机向量$ v $的协方差矩阵是所有RV对之间的协方差的矩阵。实际上,我们可以将其视为对单个RV的方差的扩展。
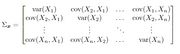
我们可以从定义出发进行推导得到一个推论,注意下面多处包含的是向量的外积:
Σ v = E [ ( v − μ v ) ( v − μ v ) T ] = E [ v v T − v μ v T − μ v v T + μ v μ v T ] = E [ v v T ] − E [ v μ v T ] − E [ μ v v T ] + E [ μ v μ v T ] = E [ v v T ] − E [ v ] μ v T − μ v E [ v T ] + μ v μ v T = E [ v v T ] − μ v μ v T − μ v μ v T + μ v μ v T = E [ v v T ] − μ v μ v T \Sigma_{v} = E[(v-\mu_v)(v-\mu_v)^T] \\\\ = E[vv^T - v\mu_v^T - \mu_vv^T + \mu_v\mu_v^T] \\\\ = E[vv^T] - E[v\mu_v^T] - E[\mu_v v^T] + E[\mu_v \mu_v^T] \\\\ = E[vv^T] - E[v]\mu_v^T - \mu_v E[v^T] + \mu_v\mu_v^T \\\\ = E[vv^T] - \mu_v \mu_v^T - \mu_v \mu_v^T + \mu_v\mu_v^T \\\\ = E[vv^T] - \mu_v \mu_v^T Σv=E[(v−μv)(v−μv)T]=E[vvT−vμvT−μvvT+μvμvT]=E[vvT]−E[vμvT]−E[μvvT]+E[μvμvT]=E[vvT]−E[v]μvT−μvE[vT]+μvμvT=E[vvT]−μvμvT−μvμvT+μvμvT=E[vvT]−μvμvT
性质
- 对称性
- 半正定性
参数估计
最大后验概率
Maximum-a-posteriori (MAP)。对于分类问题,MAP将0-1损失最小化。
假设 x , y x,y x,y都是离散的。
y ^ = g ( x ) = a r g m a x y p ( y ∣ x ) = a r g m a x y p ( x , y ) = a r g m a x y p ( x ∣ y ) p ( y ) \hat y = g(x) = argmax_y p(y|x) \\\\ = argmax_y p(x,y) \\\\ = argmax_y p(x|y)p(y) \\\\ y^=g(x)=argmaxyp(y∣x)=argmaxyp(x,y)=argmaxyp(x∣y)p(y)
假设 x x x是连续的, y y y是离散的。
y ^ = g ( x ) = a r g m a x y p ( y ∣ x ) = a r g m a x y f ( x ∣ y ) p ( y ) \hat y = g(x) = argmax_y p(y|x) \\\\ = argmax_y f(x|y)p(y) y^=g(x)=argmaxyp(y∣x)=argmaxyf(x∣y)p(y)
缺点
- 随机变量相互独立的假设通常不成立
- 训练集中未出现某个值的样本导致概率为0,可以通过smoothing解决
最大似然估计
Maximum Likelihood Estimation (MLE)。在MAP的基础上,我们假设 y y y的先验概率都相同。
y ^ = a r g m a x y p ( y ∣ x ) = a r g m a x y p ( x ∣ y ) \hat y = argmax_y p(y|x) \\\\ = argmax_y p(x|y) \\\\ y^=argmaxyp(y∣x)=argmaxyp(x∣y)
用 y y y表示会显得完全随机,有可能该参数是服从某个分布的,所以常用 θ \theta θ表示。在保证独立的情况下,可以得到
p θ ( x ) = ∏ i = 1 N p ( x i ) p_\theta(x) = \prod_{i=1}^N p(x_i) \\\\ pθ(x)=i=1∏Np(xi)
假设进行 n n n次伯努利实验,观察到 k k k次成功。我们想要预测其成功概率,用 θ \theta θ来表示。当 θ = k / n \theta=k/n θ=k/n时有最大值。
a r g m a x θ θ k ( 1 − θ ) n − k = a r g m a x θ l o g [ θ k ( 1 − θ ) n − k ] = a r g m a x θ [ k l o g θ + ( n − k ) l o g ( 1 − θ ) ] k / θ − ( n − k ) / ( 1 − θ ) = 0 θ ∗ = k / n argmax_\theta \theta^k(1-\theta)^{n-k} \\\\ = argmax_\theta log[\theta^k(1-\theta)^{n-k}] \\\\ = argmax_\theta[k log\theta + (n-k)log(1-\theta)] \\\\ k/\theta - (n-k)/(1-\theta) = 0 \\\\ \theta^* = k/n argmaxθθk(1−θ)n−k=argmaxθlog[θk(1−θ)n−k]=argmaxθ[klogθ+(n−k)log(1−θ)]k/θ−(n−k)/(1−θ)=0θ∗=k/n
同理,在 θ \theta θ服从高斯分布的情况下,我们可以得到 θ ∗ = 1 n ∑ x i \theta^* = \frac 1 n \sum x_i θ∗=n1∑xi。
最小二乘法
Minimum Mean Squared Error (MMSE)。最小化平方误差函数。
y ^ = f ( x ) = E [ y ∣ x ] \hat y = f(x) = E[y|x] \\\\ y^=f(x)=E[y∣x]
考虑两个向量 x x x 和 y y y 有联合分布 p ( x , y ) p(x,y) p(x,y)。我们可以得到,
E [ ( y − E [ y ∣ x ] ) 2 ] = E [ y 2 − 2 y E [ y ∣ x ] + ( E [ y ∣ x ] ) 2 ] = E [ y 2 ] − 2 E [ y E [ y ∣ x ] ] + E [ ( E [ y ∣ x ] ) 2 ] = E [ y 2 ] − 2 E [ E [ y E [ y ∣ x ] ∣ x ] ] + E [ ( E [ y ∣ x ] ) 2 ] = E [ y 2 ] − 2 E [ E [ y ∣ x ] E [ y ∣ x ] ] + E [ ( E [ y ∣ x ] ) 2 ] = E [ y 2 ] − E [ ( E [ y ∣ x ] ) 2 ] = E [ E [ y 2 ∣ x ] ] − ( E [ E [ y ∣ x ] ] ) 2 = E [ v a r ( y ∣ x ) ] E[(y - E[y|x])^2] = E[y^2 - 2yE[y|x] + (E[y|x])^2] \\\\ = E[y^2] - 2E[yE[y|x]] + E[(E[y|x])^2] \\\\ = E[y^2] - 2E[E[yE[y|x]|x]] + E[(E[y|x])^2] \\\\ = E[y^2] - 2E[E[y|x]E[y|x]] + E[(E[y|x])^2] \\\\ = E[y^2] - E[(E[y|x])^2] \\\\ = E[E[y^2|x]] - (E[E[y|x]])^2 \\\\ = E[var(y|x)] E[(y−E[y∣x])2]=E[y2−2yE[y∣x]+(E[y∣x])2]=E[y2]−2E[yE[y∣x]]+E[(E[y∣x])2]=E[y2]−2E[E[yE[y∣x]∣x]]+E[(E[y∣x])2]=E[y2]−2E[E[y∣x]E[y∣x]]+E[(E[y∣x])2]=E[y2]−E[(E[y∣x])2]=E[E[y2∣x]]−(E[E[y∣x]])2=E[var(y∣x)]
条件独立
我们认为当前概率可能与其前面发生事件的概率相关(即条件), p ( x ) = p ( x 1 ) p ( x 2 ∣ x 1 ) p ( x 3 ∣ x 1 , x 2 ) . . . p ( x n ∣ x 1 , . . . x n − 1 ) p(x) = p(x_1)p(x_2|x_1)p(x_3|x_1, x_2)\ ...\ p(x_n|x_1, \ ...\ x_{n-1}) p(x)=p(x1)p(x2∣x1)p(x3∣x1,x2) ... p(xn∣x1, ... xn−1)。
p ( x ) = ∏ j = 1 N p ( x j ∣ x 1 , x 2 , . . . , x j − 1 ) p(x) = \prod_{j=1}^N p(x_j | x_1, x_2, \ ...\ ,x_{j-1}) p(x)=j=1∏Np(xj∣x1,x2, ... ,xj−1)
需要注意的是,分解形式并不唯一,我们也可以调换分解的顺序。不过,上式是最常见的形式。
我们将X和Y两个RV相互独立记作 X ⊥ Y X \bot Y X⊥Y。
条件独立的英文是conditional independence。
X 1 X_1 X1和 X 2 X_2 X2在 X 3 X_3 X3发生时条件独立是 p ( x 1 , x 2 ∣ x 3 ) = p ( x 1 ∣ x 3 ) p ( x 2 ∣ x 3 ) p(x_1, x_2|x_3) =p(x_1|x_3)p(x_2|x_3) p(x1,x2∣x3)=p(x1∣x3)p(x2∣x3)的充要条件,记作 X 1 ⊥ X 2 ∣ X 3 X_1 \bot X_2 | X_3 X1⊥X2∣X3。我们也可以推出此时 p ( x 1 ∣ x 2 , x 3 ) = p ( x 1 ∣ x 3 ) p(x_1|x_2, x_3) = p(x_1|x_3) p(x1∣x2,x3)=p(x1∣x3)。
我们来看一个例子。我们抛一枚质地均匀的硬币两次。结果分别记为 X 1 X_1 X1和 X 2 X_2 X2,令 X 3 X_3 X3为前两者的异或结果。容易得到 p ( x 1 ) = p ( x 2 ) = p ( x 3 ) = 1 2 ; x = { 0 , 1 } p(x_1) = p(x_2) = p(x_3) = \frac {1} {2}; x = \{0,1\} p(x1)=p(x2)=p(x3)=21;x={0,1}。我们发现任意两个RV之间都是独立的,例如 X 1 X_1 X1, X 3 X_3 X3。但是当 X 3 X_3 X3发生时(已知 x 3 x_3 x3), X 1 X_1 X1和 X 2 X_2 X2之间并非独立的。
再来看一个例子。我们抛一枚质地均匀的硬币,结果记为 X 1 X_1 X1。如果结果为1,再抛一次硬币结果记为 X 2 X_2 X2,否则将 X 2 X_2 X2设为0。令 X 3 X_3 X3等于 X 2 X_2 X2。此时当 X 2 X_2 X2发生时, X 1 , X 3 X_1, X_3 X1,X3是独立的(条件独立),即 X 1 ⊥ X 3 ∣ X 2 X_1 \bot X_3 | X_2 X1⊥X3∣X2。
| X 1 X_1 X1 | X 2 X_2 X2 | X 3 X_3 X3 | p ( x 1 , x 2 , x 3 ) p(x_1, x_2, x_3) p(x1,x2,x3) |
|---|---|---|---|
| 0 | 0 | 0 | 1 2 \frac{1} {2} 21 |
| 1 | 0 | 0 | 1 4 \frac{1} {4} 41 |
| 1 | 1 | 1 | 1 4 \frac{1} {4} 41 |
概率图模型
普通的图由节点和边的集合构成。 G : = ( V , E ) G := (V, E) G:=(V,E)。通常用边表(edge list)表示。
应用包括社区发现(community detection),图向量嵌入(graph embeddings)等。
概率图模型是用图论方法以表现数个独立随机变量之间关联的一种建模方法。形式通常是有向无环图(directed acyclic graphical models, DAGs)。我们也可以称为贝叶斯网络(bayesian networks)。我们用 x ∼ p ( x ) x \sim p(x) x∼p(x)联系到图的性质中,使用一个节点代表一个RV,使用边代表不同RV间的依赖,即 p ( x ) = ∏ j p ( x j ∣ p a r e n t s o f x j ) p(x) = \prod_j p(x_j | parents\ of\ x_j) p(x)=∏jp(xj∣parents of xj)。通常情况下,我们对节点进行编号时,父节点会被先编号。
我们可以得到$X_i \bot X_j | {parents\ of X_i}\ \forall \ j < i \ & \ X_j \notin {parents\ of X_i} $。
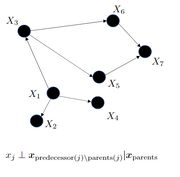
例如,在上面图示中, X 7 ⊥ X 3 ∣ X 5 , X 6 X_7 \bot X_3 | X_5, X_6 X7⊥X3∣X5,X6。
由此,我们可以得到结论
p ( x ) = ∏ j = 1 N p ( x j ∣ p a r e n t s o f x j ) p(x) = \prod_{j=1}^N p(x_j | parents\ of\ x_j) p(x)=j=1∏Np(xj∣parents of xj)
马尔科夫链
这是概率图模型的一种特殊情况,即下一状态的概率分布只由当前状态决定,在时间序列中它前面的事件均与之无关。 p ( x ) = p ( x 1 ) p ( x 2 ∣ x 1 ) p ( x 3 ∣ x 2 ) . . . p ( x n ∣ x n − 1 ) p(x) = p(x_1)p(x_2|x_1)p(x_3|x_2)...p(x_n|x_{n-1}) p(x)=p(x1)p(x2∣x1)p(x3∣x2)...p(xn∣xn−1)。
信息熵
英文是Entropy。对于每一个事件,我们从它的发生能够获取到的信息是 l o g 2 ( 1 P ( A ) ) log_2(\frac 1 {P(A)}) log2(P(A)1)。这一个公式其实是符合我们的直觉的。如果一个不寻常事件它发生了,透露的信息应该比常见事件透露的信息更多。
信息熵的定义如下,
H ( X ) = ∑ i = 1 m E [ l o g 2 1 p ( x i ) ] = − ∑ i = 1 m p ( x i ) l o g 2 p ( x i ) H(X) = \sum_{i=1}^mE[log_2 \frac{1} {p(x_i)}] = -\sum_{i=1}^m p(x_i) log_2 p(x_i) H(X)=i=1∑mE[log2p(xi)1]=−i=1∑mp(xi)log2p(xi)
性质
- H ( x ) ≥ 0 H(x) \ge 0 H(x)≥0
- H ( x ) ≤ l o g 2 ( ∣ X ∣ ) H(x) \le log_2(|\mathcal X|) H(x)≤log2(∣X∣)
通过上式,我们可以推导出联合信息熵
H ( X , Y ) = − ∑ i = 1 m ∑ j = 1 n p ( x i , y j ) l o g 2 ( p ( x i , y j ) ) H(X, Y) = -\sum_{i=1}^m\sum_{j=1}^n p(x_i, y_j) log_2 (p(x_i, y_j)) H(X,Y)=−i=1∑mj=1∑np(xi,yj)log2(p(xi,yj))
同理,可以得到条件信息熵
H ( X ∣ Y ) = − ∑ y p ( y ) H ( X ∣ Y = y ) H(X|Y) = -\sum_{y} p(y) H(X|Y=y) \\\\ H(X∣Y)=−y∑p(y)H(X∣Y=y)
实际上,通过信息熵的链式法则,我们可以使用条件信息熵得到联合信息熵。
H ( X , Y ) = H ( X ) + H ( Y ∣ X ) H(X, Y) = H(X) + H(Y|X) H(X,Y)=H(X)+H(Y∣X)
推导如下,
H ( X , Y ) = − ∑ x ∑ y p ( x , y ) l o g 2 ( p ( x , y ) ) = − ∑ x ∑ y p ( x , y ) l o g 2 ( p ( x ) ∗ p ( y ∣ x ) ) = − ∑ x ∑ y p ( x , y ) ( l o g 2 p ( x ) + l o g 2 p ( y ∣ x ) ) = − ∑ x ∑ y p ( x , y ) l o g 2 p ( x ) − ∑ x ∑ y p ( x , y ) l o g 2 p ( y ∣ x ) = − ∑ x p ( x ) l o g 2 p ( x ) − ∑ x ∑ y p ( x ) p ( y ∣ x ) l o g 2 p ( y ∣ x ) = H ( X ) − ∑ x p ( x ) H ( Y ∣ X = x ) = H ( X ) + H ( Y ∣ X ) H(X, Y) = -\sum_{x}\sum_{y} p(x, y) log_2 (p(x, y)) \\\\ = -\sum_{x}\sum_{y} p(x, y) log_2 (p(x) * p(y|x)) \\\\ = -\sum_{x}\sum_{y} p(x, y) (log_2p(x) + log_2p(y|x)) \\\\ = -\sum_{x}\sum_{y} p(x, y) log_2p(x) -\sum_{x}\sum_{y} p(x, y) log_2p(y|x) \\\\ = -\sum_{x} p(x) log_2p(x) -\sum_{x}\sum_{y} p(x)p(y|x) log_2p(y|x) \\\\ = H(X) -\sum_{x}p(x)H(Y|X=x) \\\\ = H(X) + H(Y|X) \\\\ H(X,Y)=−x∑y∑p(x,y)log2(p(x,y))=−x∑y∑p(x,y)log2(p(x)∗p(y∣x))=−x∑y∑p(x,y)(log2p(x)+log2p(y∣x))=−x∑y∑p(x,y)log2p(x)−x∑y∑p(x,y)log2p(y∣x)=−x∑p(x)log2p(x)−x∑y∑p(x)p(y∣x)log2p(y∣x)=H(X)−x∑p(x)H(Y∣X=x)=H(X)+H(Y∣X)
通过多次使用该链式法则,我们可以得到
H ( X 1 , X 2 , . . . , X n ) = ∑ i = 1 n H ( X i ∣ X 1 , X 2 , . . . , X i − 1 ) H(X_1, X_2,\ ...\ , X_n) = \sum_{i=1}^n H(X_i | X_1, X_2,\ ...\ , X_{i-1}) H(X1,X2, ... ,Xn)=i=1∑nH(Xi∣X1,X2, ... ,Xi−1)
性质
- H ( X ) ≥ H ( X ∣ Y ) H(X) \ge H(X|Y) H(X)≥H(X∣Y),已知条件减小了不确定性
- H ( X ) = H ( X ∣ Y ) ; X ⊥ Y H(X) = H(X|Y); X \bot Y H(X)=H(X∣Y);X⊥Y
- H ( X , Y ) = H ( X ) + H ( Y ) ; X ⊥ Y H(X, Y) = H(X) + H(Y); X \bot Y H(X,Y)=H(X)+H(Y);X⊥Y
- H ( X , Y ) = H ( X ) ; Y = g ( X ) H(X, Y) = H(X); Y = g(X) H(X,Y)=H(X);Y=g(X)
微分熵
是从以离散随机变量所计算出的夏农熵推广,以连续型随机变量计算所得之熵。
H ( X ) = ∫ x p ( x ) l o g 2 ( 1 p ( x ) ) d x H(X) = \int_x p(x) log_2(\frac 1 {p(x)}) dx H(X)=∫xp(x)log2(p(x)1)dx
假设 X ∼ N ( μ , σ 2 ) X \sim \mathcal N(\mu, \sigma^2) X∼N(μ,σ2)。那么 H ( X ) = 1 2 l o g 2 ( 2 π e σ 2 ) H(X) = \frac 1 2 log_2(2\pi e \sigma^2) H(X)=21log2(2πeσ2)比特(bits)。
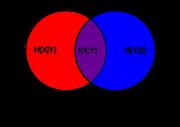
互信息
互信息被定义为 I ( Y ; X ) = H ( Y ) − H ( Y ∣ X ) I(Y;X) = H(Y) - H(Y|X) I(Y;X)=H(Y)−H(Y∣X),用于表示由于已知 X X X, Y Y Y的不确定性被减小了的部分。
性质
- I ( Y ; X ) = I ( X ; Y ) I(Y;X) = I(X;Y) I(Y;X)=I(X;Y)
- I ( Y ; X ) = ∑ x , y p ( x , y ) l o g ( p ( x , y ) p ( x ) p ( y ) ) I(Y;X) = \sum_{x, y} p(x, y) log(\frac{p(x, y)} {p(x)p(y)}) I(Y;X)=∑x,yp(x,y)log(p(x)p(y)p(x,y))
从下面这张韦恩图,我们可以直观地看见各个部分。
多变量高斯分布
我们考虑一个RV向量 x x x,期望是 μ \mu μ,有协方差矩阵 Σ x \Sigma_x Σx。可以得到联合高斯RV如下。
x ∼ N ( μ , Σ ) x \sim \mathcal N(\mu, \Sigma) x∼N(μ,Σ)
f ( x ) = 1 ( 2 π ) n ∣ Σ ∣ ∗ e − ( x − μ ) T Σ − 1 ( x − μ ) 2 f(x) = \frac {1} {\sqrt{(2\pi)^{n} |\Sigma|}} * e^{-\frac {(x-\mu)^T\Sigma^{-1}(x-\mu)} { 2}} f(x)=(2π)n∣Σ∣1∗e−2(x−μ)TΣ−1(x−μ)
因为 Σ \Sigma Σ是半正定的,我们知道 Σ − 1 \Sigma^{-1} Σ−1是半正定的。指数部分的等高线我们可以得到一个椭圆如下。
( x − μ ) T Σ − 1 ( x − μ ) ≥ 0 ; i f x − μ ≠ 0 ( x − μ ) T Σ − 1 ( x − μ ) = c (x-\mu)^T\Sigma^{-1}(x-\mu) \ge 0; \ if\ x- \mu \ne 0 \\\\ (x-\mu)^T\Sigma^{-1}(x-\mu) = c (x−μ)TΣ−1(x−μ)≥0; if x−μ=0(x−μ)TΣ−1(x−μ)=c
在最简单的情况下, x ∼ N ( 0 , I ) x \sim \mathcal N(0, I) x∼N(0,I),我们得到一个圆心在原点的圆。在一般情况下,我们需要对协方差矩阵进行分解。
Σ = U Λ U T = ∑ λ i u u T ( x − μ ) T Σ − 1 ( x − μ ) = ∑ 1 λ i ( x − μ ) T u i u i T ( x − μ ) = ∑ y i 2 λ i \Sigma = U\Lambda U^T = \sum \lambda_i uu^T \\\\ (x-\mu)^T\Sigma^{-1}(x-\mu) = \sum \frac 1 {\lambda_i} (x-\mu)^T u_i u_i^T (x-\mu) \\\\ = \sum \frac {y_i^2} {\lambda_i} Σ=UΛUT=∑λiuuT(x−μ)TΣ−1(x−μ)=∑λi1(x−μ)TuiuiT(x−μ)=∑λiyi2
这里的 y y y并没有特殊含义,只是为了书写简便,对表达式进行了简化。
性质
-
线性变换:已知 x ∼ N ( μ , Σ ) x \sim \mathcal N(\mu, \Sigma) x∼N(μ,Σ),则 A x ∼ N ( A μ , A Σ A T ) Ax \sim \mathcal N(A \mu, A \Sigma A^T) Ax∼N(Aμ,AΣAT)
-
如果RV之间无关联,即相互独立,则 Σ \Sigma Σ是对角矩阵, f ( x ) = ∏ i f ( x i ) f(x) = \prod_i f(x_i) f(x)=∏if(xi)
-
边缘概率分布(marginal)也是高斯随机变量
-
条件概率(conditional)也是高斯随机变量
对于性质1,在求边缘分布(marginal)的时候特别有用。我们一般需要通过对其他特征维度进行积分的方法求解,但我们也可以利用性质1构造一个巧妙的 A A A来求解。比如此时有三维特征,我们想求 p ( x 2 ) p(x_2) p(x2),那么我们将 A A A设置成 [ 0 1 0 ] [0\ 1\ 0] [0 1 0]即可。这个方法帮助我们省去积分的繁琐步骤。
对于性质3,要注意它反过来并不成立。即,假设边缘概率分布都是高斯随机变量,并不意味着由这些随机变量组成的RV服从高斯分布。
我们再对性质4做一些说明。通过线代,我们知道可以对矩阵做划分如下。
我们将 Σ x 2 ∣ x 1 \Sigma_{x_2|x_1} Σx2∣x1称为 Σ 11 \Sigma_{11} Σ11的舒尔补(Schur complement)。从操作上看其实非常容易理解,将 Σ \Sigma Σ取逆,将和已知条件相关的行和列去掉,再将得到的小矩阵取逆。这里的描述有些抽象,具体过程请参阅 (Murphy, 2012, 4.1-4.2)。
Σ x 2 ∣ x 1 = Σ 22 − Σ 21 Σ 11 − 1 Σ 12 \Sigma_{x_2|x_1} = \Sigma_{22} - \Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12} Σx2∣x1=Σ22−Σ21Σ11−1Σ12
由舒尔补,我们可以得到
x 2 ∣ x 1 ∼ N ( Σ 21 Σ 11 − 1 ( x 1 − μ 1 ) + μ 2 , Σ 22 − Σ 21 Σ 11 − 1 Σ 12 ) x_2|x_1 \sim \mathcal N(\Sigma_{21}\Sigma_{11}^{-1}(x_1 - \mu_1) + \mu_2, \Sigma_{22} - \Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12}) x2∣x1∼N(Σ21Σ11−1(x1−μ1)+μ2,Σ22−Σ21Σ11−1Σ12)
同理可得
x 1 ∣ x 2 ∼ N ( Σ 12 Σ 22 − 1 ( x 2 − μ 2 ) + μ 1 , Σ 11 − Σ 12 Σ 22 − 1 Σ 21 ) x_1|x_2 \sim \mathcal N(\Sigma_{12}\Sigma_{22}^{-1}(x_2 - \mu_2) + \mu_1, \Sigma_{11} - \Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}) x1∣x2∼N(Σ12Σ22−1(x2−μ2)+μ1,Σ11−Σ12Σ22−1Σ21)
高斯判别分析
我们假设观测数据来自于条件高斯分布。
p ( x ∣ y = 0 ) ∼ N ( μ 0 , Σ 0 ) p ( x ∣ y = 1 ) ∼ N ( μ 1 , Σ 1 ) p(x | y = 0) \sim \mathcal N(\mu_0, \Sigma_0) \\\\ p(x | y = 1) \sim \mathcal N(\mu_1, \Sigma_1) \\\\ p(x∣y=0)∼N(μ0,Σ0)p(x∣y=1)∼N(μ1,Σ1)
我们通过将两者的概率相除,然后取对数,就可以得到对数似然比(log likelihood ratio)。大于0的归为一类,小于0的归为另一类。
分类边界为 x T B x + w T x = c x^T B x + w^T x = c xTBx+wTx=c。如果两个高斯分布的协方差矩阵相同,那么分类边界可以简化成为 w T x = c w^T x= c wTx=c。这里我们假设两类的先验概率相同。
f ( x ) = l o g ( f ( x ∣ Y = 0 ) f ( x ∣ Y = 1 ) ) = l o g ( f ( x ∣ Y = 0 ) ) − l o g ( f ( x ∣ Y = 1 ) ) = l o g ( 1 ( 2 π ) 2 ∣ Σ 0 ∣ ∗ e − ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) 2 ) − l o g ( 1 ( 2 π ) 2 ∣ Σ 1 ∣ ∗ e − ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) 2 ) = l o g ( 1 ( 2 π ) 2 ∣ Σ 0 ∣ ) − ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) 2 − l o g ( 1 ( 2 π ) 2 ∣ Σ 1 ∣ ) + ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) 2 = l o g ( ∣ Σ 1 ∣ ∣ Σ 0 ∣ ) + 1 2 [ ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) − ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) ] = 1 2 l o g ( ∣ Σ 1 ∣ ) − 1 2 l o g ( ∣ Σ 0 ∣ ) + 1 2 [ ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) − ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) ] f(x) = log(\frac{f(x|Y=0)} {f(x|Y=1)}) \\\\ = log(f(x|Y=0)) - log(f(x|Y=1)) \\\\ = log(\frac {1} {\sqrt{(2\pi)^{2} |\Sigma_0|}} * e^{-\frac {(x-\mu_0)^T\Sigma_0^{-1}(x-\mu_0)} {2}}) - log(\frac {1} {\sqrt{(2\pi)^{2} |\Sigma_1|}} * e^{-\frac {(x-\mu_1)^T \Sigma_1^{-1} (x-\mu_1)} {2}}) \\\\ = log(\frac {1} {\sqrt{(2\pi)^{2} |\Sigma_0|}}) -\frac {(x-\mu_0)^T\Sigma_0^{-1}(x-\mu_0)} {2} - log(\frac {1} {\sqrt{(2\pi)^{2} |\Sigma_1|}}) + \frac {(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)} {2} \\\\ = log(\sqrt{\frac { |\Sigma_1|}{|\Sigma_0|}}) + \frac{1} {2} [(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1) - (x-\mu_0)^T\Sigma_0^{-1}(x-\mu_0)] \\\\ = \frac{1} {2} log({|\Sigma_1|}) - \frac{1} {2} log({|\Sigma_0|}) + \frac{1} {2} [(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1) - (x-\mu_0)^T\Sigma_0^{-1}(x-\mu_0)] \\\\ f(x)=log(f(x∣Y=1)f(x∣Y=0))=log(f(x∣Y=0))−log(f(x∣Y=1))=log((2π)2∣Σ0∣1∗e−2(x−μ0)TΣ0−1(x−μ0))−log((2π)2∣Σ1∣1∗e−2(x−μ1)TΣ1−1(x−μ1))=log((2π)2∣Σ0∣1)−2(x−μ0)TΣ0−1(x−μ0)−log((2π)2∣Σ1∣1)+2(x−μ1)TΣ1−1(x−μ1)=log(∣Σ0∣∣Σ1∣)+21[(x−μ1)TΣ1−1(x−μ1)−(x−μ0)TΣ0−1(x−μ0)]=21log(∣Σ1∣)−21log(∣Σ0∣)+21[(x−μ1)TΣ1−1(x−μ1)−(x−μ0)TΣ0−1(x−μ0)]
边界可以通过乘以常数得到
l o g ( ∣ Σ 1 ∣ ) − l o g ( ∣ Σ 0 ∣ ) + ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) − ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) = 0 x T ( Σ 1 − 1 − Σ 0 − 1 ) x + 2 ( μ 0 T Σ 0 − 1 − μ 1 T Σ 1 − 1 ) x = l o g ( ∣ Σ 0 ∣ ) − l o g ( ∣ Σ 1 ∣ ) + μ 0 T Σ 0 − 1 μ 0 − μ 1 T Σ 1 − 1 μ 1 log({|\Sigma_1|}) - log({|\Sigma_0|}) + (x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1) - (x-\mu_0)^T\Sigma_0^{-1}(x-\mu_0) = 0 \\\\ x^T (\Sigma_1^{-1} - \Sigma_0^{-1}) x + 2(\mu_0^T\Sigma_0^{-1} - \mu_1^T \Sigma_1^{-1})x = log({|\Sigma_0|}) - log({|\Sigma_1|}) + \mu_0^T\Sigma_0^{-1}\mu_0 - \mu_1^T\Sigma_1^{-1}\mu_1 \\\\ log(∣Σ1∣)−log(∣Σ0∣)+(x−μ1)TΣ1−1(x−μ1)−(x−μ0)TΣ0−1(x−μ0)=0xT(Σ1−1−Σ0−1)x+2(μ0TΣ0−1−μ1TΣ1−1)x=log(∣Σ0∣)−log(∣Σ1∣)+μ0TΣ0−1μ0−μ1TΣ1−1μ1
其中的参数如下
B = Σ 1 − 1 − Σ 0 − 1 w = 2 ( Σ 0 − 1 μ 0 − Σ 1 − 1 μ 1 ) c = l o g ( ∣ Σ 0 ∣ ) − l o g ( ∣ Σ 1 ∣ ) + μ 0 T Σ 0 − 1 μ 0 − μ 1 T Σ 1 − 1 μ 1 B = \Sigma_1^{-1} - \Sigma_0^{-1} \\\\ w = 2(\Sigma_0^{-1}\mu_0 - \Sigma_1^{-1}\mu_1) \\\\ c = log({|\Sigma_0|}) - log({|\Sigma_1|}) + \mu_0^T\Sigma_0^{-1}\mu_0 - \mu_1^T\Sigma_1^{-1}\mu_1 \\\\ B=Σ1−1−Σ0−1w=2(Σ0−1μ0−Σ1−1μ1)c=log(∣Σ0∣)−log(∣Σ1∣)+μ0TΣ0−1μ0−μ1TΣ1−1μ1
参数估计
下面是对数据中某个分类而言的,即 x i x_i xi都属于同一类别。对一组观测到的数据 x 1 , . . . , x n x_1, \ ...\ , x_n x1, ... ,xn,我们假设iid。我们看到实际上算术上的平均值就是对参数的MLE估计。
μ ^ = 1 n ∑ x i Σ ^ = 1 n ∑ ( x i − μ ^ ) ( x i − μ ^ ) T \hat \mu = \frac 1 n \sum x_i \\\\ \hat \Sigma = \frac 1 n \sum (x_i - \hat \mu)(x_i - \hat \mu)^T μ^=n1∑xiΣ^=n1∑(xi−μ^)(xi−μ^)T
下面是证明过程。这里的 L L L并不是损失Loss的意思,而是似然Likelihood。
L ( μ , Σ ) = ∏ i p μ ( x i ) = ∏ i = 1 n 1 ( 2 π ) d / 2 ∣ Σ ∣ 1 / 2 ∗ e − ( x i − μ ) T Σ − 1 ( x i − μ ) 2 l o g ( L ( μ , Σ ) ) = d n 2 l o g ( 2 π ) − n 2 l o g ( ∣ Σ ∣ ) − 1 2 ∑ i = 1 n ( x i − μ ) T Σ − 1 ( x i − μ ) L(\mu, \Sigma) = \prod_i p_{_\mu}(x_i) = \prod_{i=1}^{n} \frac {1} {(2\pi)^{d/2} |\Sigma|^{1/2}} * e^{-\frac {(x_i-\mu)^T\Sigma^{-1}(x_i-\mu)} {2}} \\\\ log(L(\mu, \Sigma)) = \frac {dn} {2} log(2\pi) - \frac {n} {2} log(|\Sigma|) - \frac {1} {2} \sum_{i=1}^{n}(x_i-\mu)^T\Sigma^{-1}(x_i-\mu) L(μ,Σ)=i∏pμ(xi)=i=1∏n(2π)d/2∣Σ∣1/21∗e−2(xi−μ)TΣ−1(xi−μ)log(L(μ,Σ))=2dnlog(2π)−2nlog(∣Σ∣)−21i=1∑n(xi−μ)TΣ−1(xi−μ)
这里给出求导定理。
∇ x a T x = a ∇ x x T A x = ( A + A T ) x ∇ X t r ( A X ) = A ∇ X l o g ∣ X ∣ = ( X − 1 ) T \nabla_x \ a^T x = a \\\\ \nabla_x \ x^T A x = (A + A^T)x \\\\ \nabla_X \ tr(AX) = A \\\\ \nabla_X log |X| = (X^{-1})^T ∇x aTx=a∇x xTAx=(A+AT)x∇X tr(AX)=A∇Xlog∣X∣=(X−1)T
我们想要求出 μ ∗ \mu^* μ∗,需要对似然进行求导。我们发现log表达式第一项是常数,第二项跟 μ \mu μ没有关系,所以直接对第三项求导。
∇ μ l o g ( L ( μ ) ) = 0 − 2 Σ − 1 x i T + 2 Σ − 1 μ = 0 Σ − 1 ∑ i ( x i − μ ) = 0 μ ∗ = 1 n ∑ i x i \nabla_\mu log(L(\mu)) = 0 \\\\ -2 \Sigma^{-1}x_i^T + 2 \Sigma^{-1} \mu = 0 \\\\ \Sigma^{-1} \sum_i(x_i - \mu) = 0 \\\\ \mu^* = \frac 1 n \sum_i x_i \\\\ ∇μlog(L(μ))=0−2Σ−1xiT+2Σ−1μ=0Σ−1i∑(xi−μ)=0μ∗=n1i∑xi
同理,我们可以求出 Σ ∗ \Sigma^* Σ∗。这个稍微麻烦一些,需要对log表达式后两项求导。我们令 Φ = Σ − 1 \Phi = \Sigma^{-1} Φ=Σ−1,对其进行求导。
∇ l o g ∣ Φ − 1 ∣ = − ( Φ − 1 ) T \nabla log|\Phi^{-1}| = -(\Phi^{-1})^T ∇log∣Φ−1∣=−(Φ−1)T
再解得 Σ \Sigma Σ。
∇ Φ l o g ( L ( Φ ) ) = 0 n 2 Φ − 1 − 1 2 ∑ ( x i − μ ) ( x i − μ ) T = 0 Σ ∗ = 1 n ∑ i ( x i − μ ) ( x i − μ ) T \nabla_\Phi log(L(\Phi)) = 0 \\\\ \frac{n} {2}\Phi^{-1} - \frac{1} {2} \sum (x_i - \mu)(x_i - \mu)^T = 0 \\\\ \Sigma^* = \frac 1 n \sum_i (x_i - \mu)(x_i - \mu)^T \\\\ ∇Φlog(L(Φ))=02nΦ−1−21∑(xi−μ)(xi−μ)T=0Σ∗=n1i∑(xi−μ)(xi−μ)T
我们无法保证协方差矩阵是满秩的(如果不是将无法取逆),所以需要加入正则化参数。 ( Σ ^ + λ I ) (\hat \Sigma + \lambda I) (Σ^+λI)可以在 λ \lambda λ为正的情况下保证满秩。当然,也有很多其他的方法。
最后,我们给出log-likelihood。
l o g L ( μ , Σ ) = − n 2 l o g ∣ Σ ∣ − ∑ i 1 2 ( x i − μ ) T Σ − 1 ( x i − μ ) log L(\mu, \Sigma) = -\frac n 2 log|\Sigma| - \sum_i \frac 1 2 (x_i-\mu)^T\Sigma^{-1}(x_i-\mu) logL(μ,Σ)=−2nlog∣Σ∣−i∑21(xi−μ)TΣ−1(xi−μ)
补充说明
上面的推导是假设了两个类别的先验概率相同。这里的推导放宽了这个限制。
L ( μ , Σ ) = p ( y = 0 ) f ( x ∣ y = 0 ) p ( y = 1 ) f ( x ∣ y = 1 ) = [ p 0 ( 2 π ) n ∣ Σ 0 ∣ ∗ e − ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) 2 ] / [ p 1 ( 2 π ) n ∣ Σ 1 ∣ ∗ e − ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) 2 ] = [ p 0 ∣ Σ 0 ∣ ∗ e − ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) 2 ] / [ p 1 ∣ Σ 1 ∣ ∗ e − ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) 2 ] L(\mu, \Sigma) = \frac {p(y=0) f(x|y=0)} {p(y=1) f(x|y=1)} \\\\ = [\frac {p_0} {\sqrt{(2\pi)^{n} |\Sigma_0|}} * e^{-\frac {(x-\mu_0)^T\Sigma_0^{-1}(x-\mu_0)} { 2}}] / [\frac {p_1} {\sqrt{(2\pi)^{n} |\Sigma_1|}} * e^{-\frac {(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)} { 2}}] \\\\ = [\frac {p_0} {\sqrt{|\Sigma_0|}} * e^{-\frac {(x-\mu_0)^T\Sigma_0^{-1}(x-\mu_0)} { 2}}] / [\frac {p_1} {\sqrt{ |\Sigma_1|}} * e^{-\frac {(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)} { 2}}] \\\\ L(μ,Σ)=p(y=1)f(x∣y=1)p(y=0)f(x∣y=0)=[(2π)n∣Σ0∣p0∗e−2(x−μ0)TΣ0−1(x−μ0)]/[(2π)n∣Σ1∣p1∗e−2(x−μ1)TΣ1−1(x−μ1)]=[∣Σ0∣p0∗e−2(x−μ0)TΣ0−1(x−μ0)]/[∣Σ1∣p1∗e−2(x−μ1)TΣ1−1(x−μ1)]
通过求对数进行简化。
l o g ( L ( μ , Σ ) ) = l o g ( p 0 ∣ Σ 0 ∣ ) − l o g ( p 1 ∣ Σ 1 ∣ ) + 1 2 [ ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) − ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) ] = 1 2 l o g ( p 0 2 ∣ Σ 0 ∣ ) − 1 2 l o g ( p 1 2 ∣ Σ 1 ∣ ) + 1 2 [ ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) − ( x − μ 0 ) T Σ 0 − 1 ( x − μ 0 ) ] log(L(\mu, \Sigma)) = \\\\ log(\frac{p_0} {\sqrt{|\Sigma_0|}}) - log(\frac{p_1} {\sqrt{|\Sigma_1|}}) + \frac{1} {2} [(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1) - (x-\mu_0)^T\Sigma_0^{-1}(x-\mu_0)] \\\\ = \frac 1 2 log(\frac{p_0^2} {|\Sigma_0|}) - \frac 1 2 log(\frac{p_1^2} {|\Sigma_1|}) + \frac{1} {2} [(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1) - (x-\mu_0)^T\Sigma_0^{-1}(x-\mu_0)] \\\\ log(L(μ,Σ))=log(∣Σ0∣p0)−log(∣Σ1∣p1)+21[(x−μ1)TΣ1−1(x−μ1)−(x−μ0)TΣ0−1(x−μ0)]=21log(∣Σ0∣p02)−21log(∣Σ1∣p12)+21[(x−μ1)TΣ1−1(x−μ1)−(x−μ0)TΣ0−1(x−μ0)]
经过推导,我们发现不平衡的类别先验概率只是影响了常数项。
B = Σ 1 − 1 − Σ 0 − 1 w = 2 ( Σ 0 − 1 μ 0 − Σ 1 − 1 μ 1 ) c = 2 l o g ( p ( y = 1 ) ) − 2 l o g ( p ( y = 0 ) ) + l o g ( ∣ Σ 0 ∣ ) − l o g ( ∣ Σ 1 ∣ ) + μ 0 T Σ 0 − 1 μ 0 − μ 1 T Σ 1 − 1 μ 1 B = \Sigma_1^{-1} - \Sigma_0^{-1} \\\\ w = 2(\Sigma_0^{-1}\mu_0 - \Sigma_1^{-1}\mu_1) \\\\ c = 2log(p(y=1)) - 2log(p(y=0)) + log({|\Sigma_0|}) - log({|\Sigma_1|}) + \mu_0^T\Sigma_0^{-1}\mu_0 - \mu_1^T\Sigma_1^{-1}\mu_1 \\\\ B=Σ1−1−Σ0−1w=2(Σ0−1μ0−Σ1−1μ1)c=2log(p(y=1))−2log(p(y=0))+log(∣Σ0∣)−log(∣Σ1∣)+μ0TΣ0−1μ0−μ1TΣ1−1μ1
我们来看一个具体的例子。

我们来计算该分类器出错的情况。
P ( y ^ ≠ y ) = p ( y = 0 ) P ( y ^ = 1 ∣ y = 0 ) + p ( y = 1 ) P ( y ^ = 0 ∣ y = 1 ) P(\hat y \ne y) = p(y=0)P(\hat y = 1|y=0) + p