集训第六天题解

A - 好奇怪的游戏

题目背景

《爱与愁的故事第三弹·shopping》娱乐章。

调调口味来道水题。

题目描述

爱与愁大神坐在公交车上无聊，于是玩起了手机。一款奇怪的游戏进入了爱与愁大神的眼帘：***（游戏名被打上了马赛克）。这个游戏类似象棋，但是只有黑白马各一匹，在点 $x_1,y_1$ 和 $x_2,y_2$ 上。它们得从点 $x_1,y_1$ 和 $x_2,y_2$ 走到 $(1,1)$。这个游戏与普通象棋不同的地方是：马可以走“日”，也可以像象走“田”。现在爱与愁大神想知道两匹马到 $(1,1)$ 的最少步数，你能帮他解决这个问题么？

输入格式

第一行两个整数 $x_1,y_1$。

第二行两个整数 $x_2,y_2$。

输出格式

第一行一个整数，表示黑马到 $(1,1)$ 的步数。

第二行一个整数，表示白马到 $(1,1)$ 的步数。

样例 #1

样例输入 #1

12 16
18 10

样例输出 #1

8 
9

提示

数据范围及约定

对于 $100\%$ 数据，$x_1,y_1,x_2,y_2\le 20$。

思路：可以从（1，1）这个点进行宽搜，然后直接输出（x1,y1),(x2,y2)
对应的最小值

#include
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,a,n) for(int i=n;i>=a;i--)
#define pb push_back
#define SZ(v) ((int)v.size())
#define fs first
#define sc second
const int N=1e5+10;
typedef long long ll;
typedef double db;
typedef pairpii;
int n,m,k,Q;
vectordel;
ll a[200010],b[200010];
int dx[15]={-2,-1,1,2,2,2,2,1,-1,-2,2,-2},
	dy[15]={2,2,2,2,1,-1,-2,-2,-2,-2,1,-1};//因为有十二个方向，所以要写两个方向增量。

int d[300][300];
int mx,my;
void bfs(int x,int y){
	queueq;
	memset(d,-1,sizeof d);
	d[x][y]=0;
	q.push({x,y});
	while(q.size()){
		auto t=q.front();
		q.pop();
		rep(i,0,12){
			int a=dx[i]+t.fs,b=dy[i]+t.sc;
			if(a>=1&&a<=20&&b>=1&&y<=20&&d[a][b]==-1){
				d[a][b]=d[t.fs][t.sc]+1;
				q.push({a,b});
			}
		}
	}
}
int main(){
	int x1,y1,x2,y2;
	cin>>x1>>y1>>x2>>y2;
	bfs(1,1);
	cout<

B - 海战

题目背景

在峰会期间，武装部队得处于高度戒备。警察将监视每一条大街，军队将保卫建筑物，领空将布满了 F-2003 飞机。

此外，巡洋船只和舰队将被派去保护海岸线。不幸的是，因为种种原因，国防海军部仅有很少的几位军官能指挥大型海战。因此，他们培养了一些新海军指挥官。军官们选择了“海战”游戏来帮助他们学习。

题目描述

在一个方形的盘上，放置了固定数量和形状的船只，每只船却不能碰到其它的船。在本题中，我们认为船是方形的，所有的船只都是由图形组成的方形。

求出该棋盘上放置的船只的总数。

输入格式

第一行为两个整数 $R$ 和 $C$，用空格隔开，分别表示游戏棋盘的行数和列数。

接下来 $R$ 行，每行 $C$ 个字符，为 # 或 .。# 表示船只的一部分，. 表示水。

输出格式

一行一个字符串，如果船的位置放得正确（即棋盘上只存在相互之间不能接触的方形，如果两个 # 号上下相邻或左右相邻却分属两艘不同的船只，则称这两艘船相互接触了）。就输出 There are S ships.，$S$ 表示船只的数量。否则输出 Bad placement.。

样例 #1

样例输入 #1

6 8
.....#.#
##.....#
##.....#
.......#
#......#
#..#...#

样例输出 #1

There are 5 ships.

提示

对于 $100\%$ 的数据，$1\le R,C\le 1000$。

思路：用bfs查找每一块区域，用两个set存储横坐标和从坐标然后将其里面有多少个元素乘起来在记录对应区域里面点有多少个，将存储的坐标乘积和区域点进行比较如果不同就就输出“Bad placement.”，如果每个区域都满足就输出区域个数

#include
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,a,n) for(int i=n;i>=a;i--)
#define pb push_back
#define SZ(v) ((int)v.size())
#define fs first
#define sc second
const int N=1e5+10;
typedef long long ll;
typedef double db;
typedef pairpii;
int n,m,k,Q;
vectordel;
ll a[200010],b[200010];
int dxtian[15]={-2,-1,1,2,2,2,2,1,-1,-2,2,-2},
	dytian[15]={2,2,2,2,1,-1,-2,-2,-2,-2,1,-1};//因为有十二个方向，所以要写两个方向增量。
int dx[4]={1,0,-1,0},
	dy[4]={0,1,0,-1};
char g[1100][1100];
bool st[1100][1100];
int sum;
void bfs(int x,int y,set &t1,set &t2){
	queueq;
	q.push({x,y});
	t1.insert(x);
	t2.insert(y);
	sum++;
	st[x][y]=1;
	while(q.size()){
		auto t=q.front();
		q.pop();
		rep(i,0,4){
			int a=dx[i]+t.fs,b=dy[i]+t.sc;
			if(a>=1&&a<=n&&b>=1&&b<=m&&!st[a][b]&&g[a][b]=='#'){
				q.push({a,b});
				st[a][b]=1;
				t1.insert(a);
				t2.insert(b);
				sum++;
			}
		}
	}
}
int main(){
	cin>>n>>m;
	rep(i,1,n){
		rep(j,1,m){
			cin>>g[i][j];
		}
	}
	int num=0;
	rep(i,1,n){
		rep(j,1,m){
			if(!st[i][j]&&g[i][j]=='#'){
				sett1,t2;
				num++;
				sum=0;
				bfs(i,j,t1,t2);
				if(t1.size()*t2.size()!=sum){
					cout<<"Bad placement.";
					return 0;
				}
			}
		}
	}
	cout<<"There are "<

C - 八皇后 Checker Challenge

题目描述

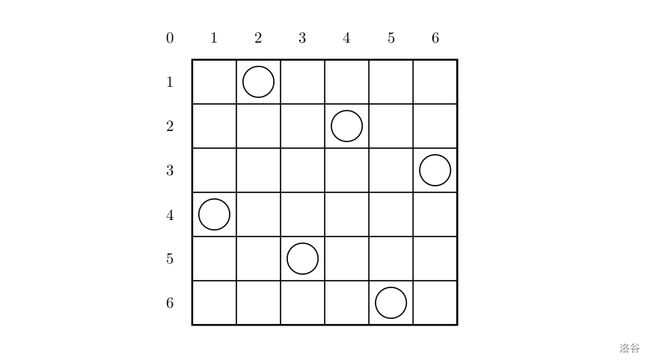
一个如下的 $6\times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

上面的布局可以用序列 $246135$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $123456$

列号 $246135$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$，表示棋盘是 $n\times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

样例 #1

样例输入 #1

6

样例输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

提示

【数据范围】
对于 $100\%$ 的数据，$6\le n\le 13$。

题目翻译来自NOCOW。

USACO Training Section 1.5

思路：将横以及斜对角正对角进行标记并将对于下标存下来

#include
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,a,n) for(int i=n;i>=a;i--)
#define pb push_back
#define SZ(v) ((int)v.size())
#define fs first
#define sc second
const int N=1e3+10;
typedef long long ll;
typedef double db;
typedef pairpii;
int n,m,k,Q;
vectordel;
ll a[200010],b[200010];
char g[N][N];
int d[N];
bool col[N],dg[N],udg[N];
int ans=0;
void dfs(int u){
    if(u==n+1){
        ans++;
           if(ans<=3){
               rep(i,1,n){
            cout<>n;
    dfs(1);
    cout<

D - 取数游戏

  # 取数游戏

题目描述

一个 $N\times M$ 的由非负整数构成的数字矩阵，你需要在其中取出若干个数字，使得取出的任意两个数字不相邻（若一个数字在另外一个数字相邻 $8$ 个格子中的一个即认为这两个数字相邻），求取出数字和最大是多少。

输入格式

第一行有一个正整数 $T$，表示了有 $T$ 组数据。

对于每一组数据，第一行有两个正整数 $N$ 和 $M$，表示了数字矩阵为 $N$ 行 $M$ 列。

接下来 $N$ 行，每行 $M$ 个非负整数，描述了这个数字矩阵。

输出格式

共 $T$ 行，每行一个非负整数，输出所求得的答案。

样例 #1

样例输入 #1

3
4 4
67 75 63 10
29 29 92 14
21 68 71 56
8 67 91 25
2 3
87 70 85
10 3 17
3 3
1 1 1
1 99 1
1 1 1

样例输出 #1

271
172
99

提示

样例解释

对于第一组数据，取数方式如下：

$$\begin{array}{cccc}[67]& 75& 63& 10\\ 29& 29& [92]& 14\\ [21]& 68& 71& 56\\ 8& 67& [91]& 25\end{array}$$

数据范围及约定

• 对于$20\%$的数据，$1\le N,\le 3$；
• 对于$40\%$的数据，$1\le N,M\le 4$；
• 对于$60\%$的数据，$1\le N,\le 5$；
• 对于$100\%$的数据，$1\le N,M\le 6$，$1\le T\le 20$。

思路：从（1，1）进行每一行进行爆搜，可以选也可以不选，当可以选的时候，将其八个方向全部标记，如果当前行搜完在搜下一行，最终和答案进行个最大值判断

#include
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,a,n) for(int i=n;i>=a;i--)
#define pb push_back
#define SZ(v) ((int)v.size())
#define fs first
#define sc second
const int N=1e5+10;
typedef long long ll;
typedef double db;
typedef pairpii;
int n,m,k,Q;
vectordel;
ll a[200010],b[200010];
int dxtian[15]={-2,-1,1,2,2,2,2,1,-1,-2,2,-2},
	dytian[15]={2,2,2,2,1,-1,-2,-2,-2,-2,1,-1};//因为有十二个方向，所以要写两个方向增量。
int dx[4]={1,0,-1,0},
	dy[4]={0,1,0,-1};//上下左右 
char g[1100][1100];
bool st[1100][1100];
int mark[20][20];
int d[8][2]={1,0,-1,0,0,1,0,-1,1,1,-1,1,1,-1,-1,-1};
int s[20][20];
int mx,ans;
void dfs(int x,int y){
	if(y==m+1){
		dfs(x+1,1);
		return ;
	}
	if(x==n+1){
		mx=max(mx,ans);
		return ;
	}
	//不选当前值
	dfs(x,y+1);
	//选取当前值
	if(mark[x][y]==0){
		ans+=s[x][y];
		rep(i,0,7){
			++mark[x+d[i][0]][y+d[i][1]];
		}
		dfs(x,y+1);
		//回溯
		ans-=s[x][y];
		rep(i,0,7){
			--mark[x+d[i][0]][y+d[i][1]];
		}
	}
}
int main(){
	int t;
	cin>>t;
	while(t--){
		cin>>n>>m;
		memset(s,0,sizeof s);
		memset(mark,0,sizeof mark);
		rep(i,1,n){
			rep(j,1,m){
				cin>>s[i][j];
			}
		}
		mx=0;
		dfs(1,1); 
		cout<

F - 数的划分

题目描述

将整数 $n$ 分成 $k$ 份，且每份不能为空，任意两个方案不相同（不考虑顺序）。

例如：$n=7$，$k=3$，下面三种分法被认为是相同的。

$1,1,5$;
$1,5,1$;
$5,1,1$.

问有多少种不同的分法。

输入格式

$n,k$ （$6<n\le 200$，$2\le k\le 6$）

输出格式

$1$ 个整数，即不同的分法。

样例 #1

样例输入 #1

7 3

样例输出 #1

4

提示

四种分法为：
$1,1,5$;
$1,2,4$;
$1,3,3$;
$2,2,3$.

【题目来源】

NOIP 2001 提高组第二题

思路：深搜，定义三维，第一维记录上次是从个数转换来的，第二维记录上次的算了后的和，第三维记录当前是第几个数了，这里循环要从last~（sum+i*(m-cur)循环保证至少存在一个i循环下去

#include
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,a,n) for(int i=n;i>=a;i--)
#define pb push_back
#define SZ(v) ((int)v.size())
#define fs first
#define sc second
const int N=1e5+10;
typedef long long ll;
typedef double db;
typedef pairpii;
int n,m,k,Q;
vectordel;
ll a[200010],b[200010];
int dxtian[15]={-2,-1,1,2,2,2,2,1,-1,-2,2,-2},
	dytian[15]={2,2,2,2,1,-1,-2,-2,-2,-2,1,-1};//因为有十二个方向，所以要写两个方向增量。
int dx[4]={1,0,-1,0},
	dy[4]={0,1,0,-1};//上下左右 
char g[1100][1100];
bool st[1100][1100];
int mark[20][20];
int d[8][2]={1,0,-1,0,0,1,0,-1,1,1,-1,1,1,-1,-1,-1};
int s[20][20];
int mx,ans,res;
void dfs(int last,int sum,int cur){
	if(cur==m){
		if(sum==n)ans++;
		return ;
	}
	for(int i=last;sum+i*(m-cur)<=n;i++){
		dfs(i,sum+i,cur+1);
	}
}
int main(){
	cin>>n>>m;
	dfs(1,0,0);
	cout<

G - 马的遍历

题目描述

有一个 $n\times m$ 的棋盘，在某个点 $(x,y)$ 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

输入格式

输入只有一行四个整数，分别为 $n,m,x,y$。

输出格式

一个 $n\times m$ 的矩阵，代表马到达某个点最少要走几步（不能到达则输出 $-1$）。

样例 #1

样例输入 #1

3 3 1 1

样例输出 #1

0    3    2    
3    -1   1    
2    1    4

提示

数据规模与约定

对于全部的测试点，保证 $1\le x\le n\le 400$，$1\le y\le m\le 400$。

思路：宽搜，这题难点就是确定dx，dy，其他做法就简单的bfs

#include
using namespace std;
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,a,n) for(int i=n;i>=a;i--)
#define pb push_back
#define SZ(v) ((int)v.size())
#define fs first
#define sc second
const int N=1e5+10;
typedef long long ll;
typedef double db;
typedef pairpii;
int n,m,k,Q;
vectordel;
ll a[200010],b[200010];
int dxtian[15]={-2,-1,1,2,2,2,2,1,-1,-2,2,-2},
	dytian[15]={2,2,2,2,1,-1,-2,-2,-2,-2,1,-1};//因为有十二个方向，所以要写两个方向增量。
int dxsi[4]={1,0,-1,0},
	dysi[4]={0,1,0,-1};//上下左右 
char g[1100][1100];
bool st[1100][1100];
int mark[20][20];
int dxy[8][2]={1,0,-1,0,0,1,0,-1,1,1,-1,1,1,-1,-1,-1};//周围8个位置 
int dx[8]={-1,-2,-2,-1,1,2,2,1},
	dy[8]={2,1,-1,-2,2,1,-1,-2};
int s[20][20];
int d[500][500];
int mx,ans,res;
void bfs(int x,int y){
	queueq;
	q.push({x,y});
	d[x][y]=0;
	while(q.size()){
		auto t=q.front();
		q.pop();
		rep(i,0,7){
			int a=dx[i]+t.fs,b=dy[i]+t.sc;
			if(a>=1&&a<=n&&b>=1&&b<=m&&d[a][b]==-1){
				q.push({a,b});
				d[a][b]=d[t.fs][t.sc]+1;
			}
		}
	}
}
int main(){
	int x,y;
	cin>>n>>m>>x>>y;
	memset(d,-1,sizeof d);
	bfs(x,y);
	rep(i,1,n){
		rep(j,1,m){
			cout<