深度学习的低秩优化:在紧凑架构和快速训练之间取得平衡（上）

论文出处：[2303.13635] Low Rank Optimization for Efficient Deep Learning: Making A Balance between Compact Architecture and Fast Training (arxiv.org)

由于篇幅有限，本篇博客仅引出问题的背景、各种张量分解方法及其分解FC/Conv层的方法，欢迎各位讨论！

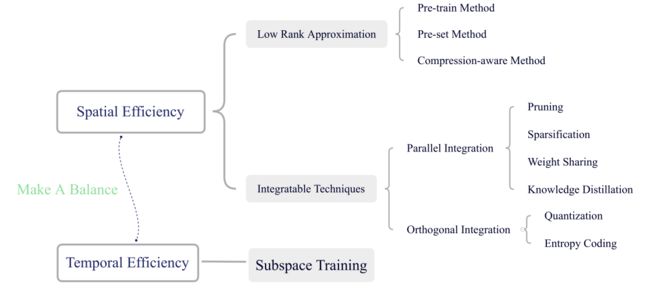
高度的计算复杂度和存储成本使得深度学习难以在资源受限的设备上使用，并且不环保，功耗高。本文专注于高效深度学习技术的低秩张量优化方法。在空间域，深度神经网络通过对网络参数进行低秩逼近( low rank approximation )进行压缩，以更少的网络参数直接降低了存储需求。在时域中，网络参数可以在几个子空间中进行训练，从而实现快速收敛的高效训练。这两种类型可以通过低秩优化联系起来，发现时域和空间域的冗余是同源的，为了加快神经网络的训练速度，需要在空间效率和时间效率之间取得平衡。

一、问题背景

1. 深度学习主要有两个挑战：高复杂性和慢收敛性。

   • 高复杂性意味着深度神经网络中有数百万个参数，大量参数和输入之间的计算非常麻烦，这强调了对高效算法的压缩和加速的需求，尤其是资源有限的设备(如手机、物联网设备)。此外，由于更深或更宽的结构可以带来更好的性能，深度神经网络逐渐以其过度参数化为特征，过度参数化意味着DNN中冗余过多，导致过拟合。

   • 传统的BP算法收敛速度慢，训练时间长。同时，收敛速度对学习率的设置和初始化权值的方式也很敏感。

2. 降低深度神经网络的高复杂性分为两类：减少参数量，减少数据表示的平均位宽。

   • 减少参数量的方法：low rank approximation（本文的重点）, pruning, weight-sharing, sparsity, knowledge distillation

   • 减少数据表示的平均位宽：Quantization 与 entropy coding

3. 模型压缩的低秩优化分为三大类：预训练方法、预设置方法和压缩感知方法( 区别在于训练的方式 )

   • 预训练方法直接对预训练模型进行分解，得到压缩格式的热初始化，然后对压缩模型进行再训练，恢复性能。

   • 预设置方法在没有预训练的情况下，从头开始训练一个预先设置为紧凑格式的网络。

   • 与上述两种方法不同的是，压缩感知方法通过逐步使网络具有低秩结构，明确地考虑了训练过程中的压缩。

   虽然关于低秩优化的讨论也可以在[2302.09019] Tensor Networks Meet Neural Networks: A Survey and Future Perspectives (arxiv.org)中找到，但本文进一步研究了如何将其与其他压缩技术相结合以追求更低的复杂度，并推荐将有效秩作为低秩优化中使用的最有效度量。

4. 加快深度神经网络的收敛速度：子空间训练

   • 一阶优化方法存在一些固有的缺陷，如理论和经验收敛速度慢。

   • 二阶方法可以很好地处理这类问题，但由于计算量大不适用预DNN。将参数投影到由多个自变量表示的微小子空间上是解决这一问题的有效方法，它只有少数变量需要优化。

二、模型压缩的低秩优化

量化、剪枝和低秩逼近等压缩方法可以在不显著降低精度的前提下降低DNN的复杂度。其中，由于张量分解具有坚实的理论基础，低秩近似被广泛采用。

(一) 网络压缩的各种张量分解方法

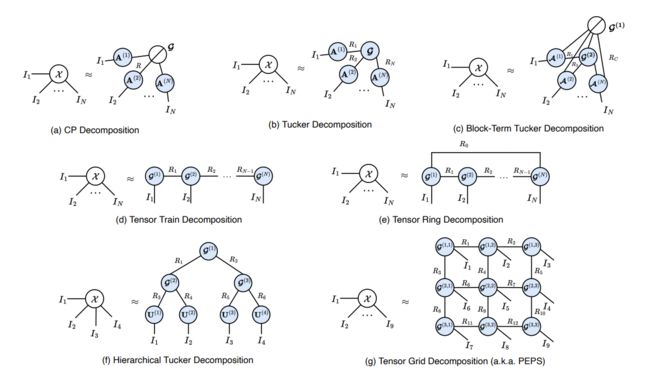
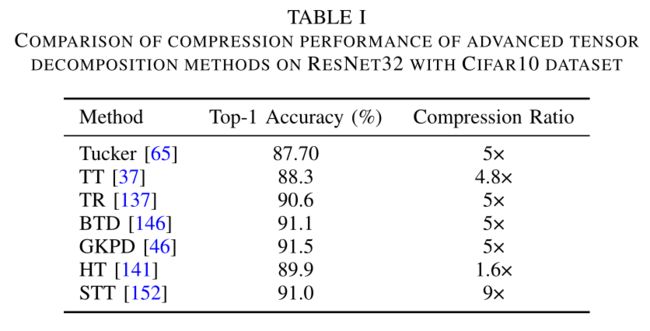
低秩近似可以在精度损失较小的情况下为递归神经网络提供超高的压缩比。然而，当涉及到卷积神经网络(CNN)时，压缩性能并不像RNN那样令人满意。将4D卷积核重构为矩阵，并利用奇异值分解(SVD)将矩阵分解为两个因子的操作，会导致结构信息失真。因此，更有效的张量分解引起了人们的兴趣。应用CP分解将卷积层分解为四个连续的卷积层，显著加快了CNN的速度。Tucker分解利用通道冗余将四维核分解为一个四维紧核和两个矩阵。在这三种经典分解的基础上，出现了许多其他灵活的方法，包括HT， TT ， TR， BTD， GKPD，基于半张量积(STP)的张量分解等，这些方法显著提高了DNN的压缩性能。表1给出了使用Cifar10数据集压缩ResNet32的常用张量分解方法的性能。

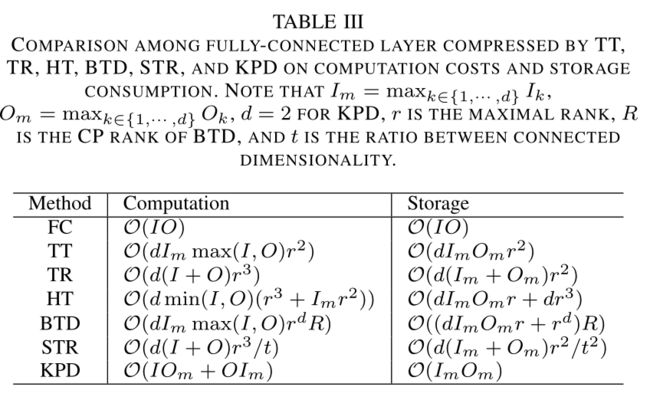
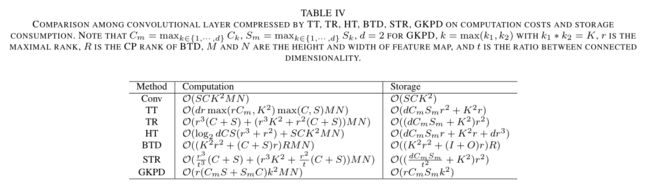
不同方法的时空复杂度，针对FC层，对比如表3所示。表4为Conv层。

对于张量的基础表示、运算就不在这里展开了，推荐一些学习资料：

浅谈张量分解（二）：张量分解的数学基础 (zhihu.com)

张量基础| 张量的秩与秩一张量 - 知乎 (zhihu.com)

( Xinyu Chen - 知乎 (zhihu.com)

Tensor Computation for Data Analysis | SpringerLink

下面介绍一下本文提到的9种分解方式：

1) Singular Value Decomposition

对于给定矩阵$X\in R^{N\times N}$，其SVD可以写成：

$$X=Udiag(s)V^T$$

设R为矩阵的秩，$R\le min(M,N)$。注意，$U\in R^{M\times N}$和$V\in R^{N\times R}$分别满足$U{U}^T=I$和$V{V}^T=I$。而$s\in {\mathbb{R}}^R$的元素依次递减，即$s_1\ge s_2\ge ...\ge s_R$。

由于FC层的权值格式是自然矩阵，因此可以直接利用奇异值分解。利用奇异值分解(SVD)，可以将FC层近似为两个连续的层。第一层和第二层的权重可以分别表示为$B=diag(\sqrt{s})V^T$和$A=Udiag(\sqrt{s})$。对于Conv层，首先要将4D核重构为2D矩阵。通过利用不同类型的冗余，有两种分解方案，一种是将W重塑为$S-by-CHW$矩阵，即信道分解，另一种是空间分解，得到$SH-by-CW$矩阵。然后，计算重构矩阵的SVD。与压缩FC层的过程类似，可以使用由因子$B$和$A$重塑的张量表示的两个Conv层来替换原始层。

然而，这两种方法都只能利用一种冗余。此外，输入通道之间也存在冗余。可以通过张量分解同时利用各种冗余，帮助我们获得更高的压缩比。

2) CP Decomposition

SVD将一个矩阵分解为秩一矩阵的和，而CP分解将一个张量分解为秩一张量（rank-one tensors）的和。对于n阶张量$\mathcal{X}\in R^{I_1\times I_2\times \cdot \cdot \cdot \times I_N}$, CP分解可表示为:

$$\mathcal{X}=[[\lambda ;{\mathbf{A}}^{(1)},{\mathbf{A}}^{(2)},\cdots ,{\mathbf{A}}^N]]=\sum _{r=1}^R{\lambda }_r{\mathbf{a}}_r^{(1)}\circ {\mathbf{a}}_r^{(2)}\circ \cdots \circ {\mathbf{a}}_r^{(N)}.$$

每个${\mathbf{a}}_r^{(n)}$表示$A^{(n)}$的第$r$列，$\lambda \in {\mathbb{R}}^R$表示$r$个分量的显著性。张量$\mathcal{X}$的秩用$R$表示，定义为秩1张量的最小个数。

在使用CP压缩FC层时，首先需要将权值矩阵W张成一个2d阶张量$\mathcal{W}\in R^{O_1\times O_2\cdot \cdot \times O_d\times I_1\times I_2\times \cdot \cdot \cdot \times I_d}$。同时，输入向量$x\in R^I$应表示为一个$d$阶张量$x\in R^{I_1\times I_2\times \cdot \cdot \cdot \times I_d}$。对于卷积核，通过直接对4-D核张量执行CP，层将由四个连续的卷积层近似，其权重分别由四个因子矩阵表示。

3) Tucker Decomposition

Tucker分解可以看作是主成分分析(PCA)的一种高阶推广。它表示一个n阶张量和一个n阶核心张量沿着每个模态乘以一个基矩阵。因此，对于$\mathcal{X}\in R^{I_1\times I_2\times \cdot \cdot \cdot \times I_N}$，有：

$$\mathcal{X}=\mathcal{G}{\times }_1{\mathbf{A}}^{(1)}{\times }_2{\mathbf{A}}^{(2)}{\times }_3\cdots {\times }_N{\mathbf{A}}^{(N)}$$

其中$\mathcal{G}\in {\mathbb{R}}^{R_1\times R_2\times \cdots \times R_N}$称为核心张量。其中，" $\times {}_n$ “表示$n$模积，即张量与模态为$n$的矩阵相乘。在元素上，” $\times{ }_{n} $”可以表示为：

$${\left(\mathcal{G}\times {}_1{\mathbf{A}}^{(1)}\right)}_{i_1,r_2,\cdots ,r_N}=\sum _{r_1=1}^{R_1}{\mathcal{G}}_{r_1,r_2,\cdots ,r_N}{\mathbf{A}}_{i_1,r_1}^{(1)}$$

因子矩阵$A(n)\in R^{I_n\times R_n}$的列可以看作是第n个模态的主成分。核心张量$\mathcal{G}$可以看作是$\mathcal{X}$的压缩版本，或者是低维子空间中的系数。在这种情况下，我们可以说$\mathcal{X}$是一个$rank-(R_1,R_2，\cdot \cdot \cdot ，R_N)$张量

在压缩FC层的情况下，与CP类似，通过直接对二阶张量进行Tucker分解对权重和输入进行相同的紧凑化。对于Conv层，由于内核的空间大小太小，我们可以只使用Tucker2利用滤波器之间和输入通道之间的冗余，生成1×1卷积、H × W卷积和1×1卷积。

4) Block Term Decomposition

块项分解(Block Term Decomposition, BTD)在中作为一种更强大的张量分解被引入，它结合了CP分解和Tucker分解。因此，BTD比原始的CP和Tucker分解具有更强的鲁棒性。CP近似于一个张量的秩一张量的和，而BTD是一个低秩Tucker格式的张量的和。或者，通过将每个模态中的因子矩阵串联起来，将每个子张量的所有核心张量排列成一个块对角核心张量，BTD可以视为Tucker的一个实例。因此，考虑一个n阶张量$\mathcal{X}\in R^{I_1\times I_2\times \cdot \cdot \cdot \times I_d}$，其BTD可以表示为:

$$\mathcal{X}=\sum _{n=1}^N{\mathcal{G}}_n{\times }_1{\mathbf{A}}_n^{(1)}{\times }_2{\mathbf{A}}_n^{(2)}{\times }_3\cdots {\times }_d{\mathbf{A}}_n^{(d)}$$

上式中，N表示CP秩，即块项个数，$\mathcal{G}\in {\mathbb{R}}^{R_1\times R_2\times \cdots \times R_d}$是第N个多线性秩块项的核心张量，其秩为$(R_1,R_2，\cdot \cdot \cdot ，R_d)$。

当BTD应用于压缩FC层时，生成的紧凑层称为块项层(Block Term layer, BTL)。在BTL中，输入张量$\mathcal{X}\in R^{I_1\times I_2\times \cdot \cdot \cdot \times I_d}$从原始输入向量$X\in R^I$张量化，原始权矩阵W被重塑为$W\in R^{O_1\times I_1\times O_2\times I_2\cdot \cdot \times O_d\times I_d}$

然后，我们可以通过BTD用因子张量{$A_n^{(d)}\in R^{Od\times Id\times Rd}$}${}_{n=1}^d$分解W。通过在$BTD(\mathcal{W})$和$\mathcal{X}$之间进行张量收缩算子，得到输出张量$\mathcal{Y}\in R^{O_1\times O_2\times \cdot \cdot \cdot \times O_d}$，可以将其矢量化作为最终的输出向量。

对于Conv层，文献声称通过将4D核重构为矩阵$W\in R^{S\times CHW}$，可以将该层转化为BTL。具体来说，矩阵应进一步重构为$1\times H\times 1\times W\times S_1\times C_1\times S_2\times C_2\times \cdot \cdot \cdot \times S_d\times C_d$。

5) Hierarchical Tucker Decomposition

分层Tucker分解(HT)是Tucker分解的一种分层变体，它迭代地表示一个高阶张量和两个低阶子张量以及利用Tucker分解得到的传递矩阵。对于张量$\mathcal{X}\in R^{I_1\times I_2\times \cdot \cdot \cdot \times I_N}$，我们可以简单地将索引集{1,2，···，N}划分为两个子集，即$T=\{t_1,t_2，\cdot \cdot ，t_k\}，S=\{s_1,s_2，\cdot \cdot ，s_{N-k}\}$

设$U_{12\cdot \cdot \cdot N}\in R^{I_{t_1}{I}_{t_2}\cdot \cdot \cdot I_{t_k}{I}_{s_1}{I}_{s_2}\cdot \cdot \cdot I_{s_{N-k}}\times 1}$表示由X重构的矩阵，截断的矩阵$U_t\in R^{I_{t_1}{I}_{t_2}\cdot \cdot \cdot I_{t_k}\times R_t}$,$U_s\in R^{I_{s_1}{I}_{s_2}\cdot \cdot \cdot I_{s_{N-k}}\times R_s}$表示两个子空间对应的列基矩阵。然后，我们可以：

$$U_{12\cdot \cdot \cdot N}=(U_t\otimes U_s)B_{12\cdot \cdot \cdot N},$$

其中$B_{12\cdot \cdot N}\in R^{R_t{R}_s\times 1}$被称为转移矩阵，“⊗”表示两个矩阵之间的Kronecker乘积。随后，将集合$\mathbb{T}$划分为两个子集$\mathbb{L}=\{l_1，l_2，\cdot \cdot \cdot ，l_q\}$和$\mathbb{V}=\{v_1，v_2，\cdot \cdot \cdot ，v_{k-q}\}$。我们可以将$U^l\in {\mathbb{R}}^{I_{l_1}{I}_{l_2}\cdot \cdot I_{l_q}\times R_l}$，$$U^v\in {\mathbb{R}}^{I_{v_1}{I}_{v_2}\cdot \cdot I_{v_q}\times R_v}$$,$U^t\in {\mathbb{R}}^{I_{t_1}{I}_{t_2}\cdot \cdot I_{t_q}\times R_t}$的$U_t$表示为：

$$U_t=(U_l\otimes U_v)B_t$$

类似的因子分解过程同时适用于$U_s$。通过重复这个过程直到索引集不能被划分，我们最终可以获得目标张量的树状HT格式。

通过HT实现FC层压缩，则需要将权重矩阵变换为$\mathcal{W}\in {\mathbb{R}}^{\left(I_1\cdot O_1\right)\times \left(I_2\cdot O_2\right)\times \cdot \cdot \times \left(I_d\cdot O_d\right)}$，并将输入数据张量化为$\mathcal{X}\in R^{I_1\times I_2\times \cdot \cdot \cdot \times I_d}$。为了降低计算复杂度，采用了图中所示的链式计算。然而，由于没有将卷积和收缩相关联的定律，因此必须从HT格式中恢复Conv层的内核。顺便说一下，为了保持平衡，4D核应该张量化为$\mathcal{W}\in R^{\left(H\cdot W\right)\times \left(C_1\cdot S_1\right)\times \left(C_2\cdot S_2\right)\times \cdot \cdot \times \left(C_d\cdot S_d\right)}$。

6) Tensor Train Decomposition

张量序列（TT）是HT的一个特例，它是退化的HT格式。TT将高阶张量分解为三阶或二阶张量的集合。这些核心张量是通过收缩算子连接起来的。假设我们有一个N阶张量，$\mathcal{X}\in R^{I_1\times I_2\times \cdot \cdot \times I_N}$，在元素上，我们可以将其分解为TT格式：

$${\mathcal{X}}_{i_1,i_2,\cdot \cdot \cdot ,i_N}=\sum _{r_1,r_2,\cdot \cdot \cdot ,r_N}{\mathcal{G}}_{i_1,r_1}^1{\mathcal{G}}_{r_1,i_2,r_2}^2\cdot \cdot \cdot {\mathcal{G}}_{r_{N-1},i_N}^N$$

其中$\{{\mathcal{G}}_n\in {\mathbb{R}}^{R_{n-1}\times I_n\times R_n}{\}}_{n=1}^N$与$R_0=1$和$R_n=1$的集合称为TT核。秩$\{Rn{\}}_{n＝0}^N$的集合称为TT秩。

TT用于压缩FC层，其中权重矩阵被重塑为高阶张量，$\mathcal{W}\in {\mathbb{R}}^{\left(I_1\cdot O_1\right)\times \left(I_2\cdot O_2\right)\times \cdot \cdot \times \left(I_d\cdot O_d\right)}$。在以TT格式表示$\mathcal{W}$之后，得到的TT核$\{{\mathcal{G}}_n\in {\mathbb{R}}^{R_{n-1}\times I_n\times O_n\times R_n}{\}}_{n=1}^N$可以与张量化输入直接收缩。[141]中提出，TT比HT更有效地压缩Conv层，而HT更适合于压缩权重矩阵更倾向于重塑为平衡张量的FC层。

[37]中介绍了在Conv层上使用TT，其中4D核张量应重塑为$（H\cdot W）\times （C_1\cdot S_1）\times （C_2\cdot S_2）\times \cdot \cdot \cdot \times （C_d\cdot S_d）$的大小，并且输入特征图重塑为$X\in {\mathbb{R}}^{H\times W\times C_1\times \cdot \cdot \cdot \times C_d}$。在前馈阶段，张量化的输入X将与每个TT核心逐一收缩。尽管TT可以显著节省存储成本，但计算复杂度可能高于原始的Conv层。因此，[149]中提出了HODEC（高阶分解卷积），以同时降低计算和存储成本，从而将每个TT核心进一步分解为两个三阶张量。

7) Tensor Ring Decomposition

由于边缘TT核的不统一（即$R_0=1$和$R_n=1$），如何排列张量的维数以找到最优的TT格式仍然是一个悬而未决的问题。为了解决这个问题，张量环（TR）分解提出了在核上进行循环多线性乘积的分解。考虑一个给定的张量，$\mathcal{X}\in R^{I_1\times I_2\times \cdot \cdot \times I_N}$，在元素上，我们可以将其TR表示公式化为：

$${\mathcal{X}}_{i_1,i_2,\cdot \cdot \cdot ,i_N}=\sum _{r_1,r_2,\cdot \cdot \cdot ,r_N}{\mathcal{G}}_{r_1,i_1,r_2}^1{\mathcal{G}}_{r_2,i_2,r_3}^2\cdot \cdot \cdot {\mathcal{G}}_{r_N,i_N,r_1}^N=tr(\sum _{r_2,\cdot \cdot \cdot ,r_N}{\mathcal{G}}_{:,i_1,r_2}^1{\mathcal{G}}_{r_2,i_2,r_3}^2\cdot \cdot \cdot {\mathcal{G}}_{r_N,i_N,:}^N)$$

其中所有核$\{{\mathcal{G}}_n\in {\mathbb{R}}^{R_n\times I_n\times R_{n+1}}{\}}_{n=1}^N$且$R_{N+1}=R_1$称为TR核。这种形式相当于$R_1$ TT形式的总和。得益于通过使用迹操作（trace operation）获得的循环多线性乘积，TR等效地对待所有核心，并变得比TT更强大和通用。

此外，由于循环策略，TR修正了TT中梯度的变化性。因此，TR也适用于压缩FC层。在[137]中，TR首次被用于压缩DNN。具体来说，FC层的权重矩阵应该被重塑为大小为$I_1\times \cdot \cdot \times I_d\times O_1\times \cdot \times O_2$的2阶张量，然后将张量表示为TR格式。对于前馈过程，首先将前d个核和后d个核合并，分别得到${\mathcal{F}}_1\in {\mathbb{R}}^{R_1\times I_1\times \cdot \cdot \times I_d\times R_{d+1}}$和${\mathcal{F}}_2\in {\mathbb{R}}^{R_{d+1}\times O_1\times \cdot \cdot \times O_d\times R_1}$。然后，我们可以计算输入$\mathcal{X}\in R^{I_1\times I_2\times \cdot \cdot \times I_d}$和${\mathcal{F}}_1$之间的收缩，得到一个可以用${\mathcal{F}}_2$收缩的矩阵。最终输出张量的大小为$O_1\times O_2\times \cdot \cdot \times O_d$。对于Conv层，如果将核张量保持在4阶并保持空间信息，则其TR格式可以公式化为：

$$K_{s,c,h,w}=\sum _{r_1=1}^{R_1}\sum _{r_2=1}^{R_2}\sum _{r_3=1}^{R_3}{\mathcal{U}}_{r_1,s,r_2}{\mathcal{V}}_{r_2,c,r_3}{\mathcal{Q}}_{r_3,h,w,r_1}$$

因此，原始层可以由三个连续层表示，其权重张量分别为$\mathcal{V}、\mathcal{Q}和\mathcal{U}$。如果需要更高的压缩比，我们可以进一步将$\mathcal{U}$和$\mathcal{V}$分别视为从$d$个核心张量合并而来的张量，从而增加合并的计算负担。

8) Generalized Kronecker P.roduct Decomposition

Kronecker乘积分解（KPD）可以将矩阵分解为由Kronecker积互连的两个较小的因子矩阵，这在应用于压缩RNNs时非常有效。为了进一步压缩Conv层，它被生成为广义Kronecker积分解（GKPD），它通过两个因子张量之间的多维Kronecker乘积的和来表示张量。形式上，$A\in R^{J_1\times J_2\times \cdot \cdot \times J_N}$和$B\in R^{K_1\times K_2\times \cdot \cdot \cdot \times K_N}$之间的多维Kronecker乘积公式化为：

$$(A\otimes B{)}_{i_1,i_2,\cdot \cdot \cdot ,i_N}={\mathcal{A}}_{j_1,j_2,\cdot \cdot \cdot ,j_N}{B}_{k_1,k_2,\cdot \cdot \cdot ,k_N}$$

其中$j_n＝b{i}_n/K_{n}c$并且$k_n＝i_{n}mod{K}_n$。基于此，对于给定的N阶张量$\mathcal{X}\in R^{J_1{K}_1\times J_2{K}_2\times \cdot \cdot \cdot \times J_N{K}_N}$，GKPD可以表示为：

$$\mathcal{X}=\sum _{r=1}^R{\mathcal{A}}_r\otimes {\mathcal{B}}_r$$

其中R被称为Kronecker秩。为了在给定$R$的GKPD中找到最佳逼近，我们可以将这个优化问题转化为找到矩阵的最佳秩-$R$逼近，$SVD$可以通过小心地将$\mathcal{X}$重新排列成矩阵，并将$\mathcal{A}$和$\mathcal{B}$重新排列成向量来方便地求解。

为了实现使用GKPD对Conv层进行解压缩，4D内核表示为：

$W_{s,c,h,w}={\sum }_{r=1}^R({\mathcal{A}}_r{)}_{s_1,c_1,h_1,w_1}\otimes ({\mathcal{B}}_r{)}_{s_2,c_2,h_2,w_2}$

其中$S_1{S}_2=S，C_1{C}_2=C，H_1{H}_2=H，W_1{W}_2=W$。每个$A_r\otimes B_r$和输入之间的2D卷积可以转换为深度等于$C_2$的3D卷积，然后是多个2D卷积。此外，$R$ Kronecker乘积组可以看作是分别计算上述两个步骤的$R$个平行通道。分析表明，较大的$S_1$和$C_2$有助于获得更多的FLOP减少。

9) Semi-tensor Product-based Tensor Decomposition

半张量积（STP）是传统矩阵积的一代，它将二维匹配矩阵的计算扩展到二维任意矩阵的计算。由于张量收缩是基于传统的矩阵乘积，我们可以将STP进一步替换为张量收缩，这将导致更通用、更灵活的张量分解方法。在[152]中提出，基于半张量乘积的张量分解旨在通过用STP代替张量收缩中的传统矩阵乘积来增强Tucker分解、TT分解和TR分解的灵活性，这表明了比原始方法高得多的效率。考虑一个特殊情况，其中列的数量$X\in {\mathbb{R}}^{M\times NP}$与$W\in {\mathbb{R}}^{P\times Q}$中的行的数量成比例，STP可以表示为：

或者，元素表示为：

$$Y_{m,g(n,q)}=\sum _{p=1}^P{X}_{m,g(n,p)}{W}_{p,q}$$

注意，$Y\in {\mathbb{R}}^{M\times NQ}$，$g(N,Q)=(Q-1)N+n和g(N,p)=(p-1)N+n$是重索引函数。

因此，以基于STP的Tucker分解为例，即STTu，可以公式化为：

其中$\mathcal{G}\in {\mathbb{R}}^{R_1\times R_2\times \cdot \cdot \times R_N}，A^{(n)}\in {\mathbb{R}}^{I_n/t\times R_n/t}$。与普通Tucker相比，参数的数量从$({\prod }_{n=0}^N{R}_n+{\sum }_{n=1}^N{I}_n{R}_n)$减少到$({\prod }_{n=0}^N{R}_n+{\sum }_{n=1}^N{I}_n{R}_n/t^2)$。

(二) 低秩逼近的优化方法

我们已经介绍了各种张量分解方法，但如何在不显著降低精度的情况下将这些方法应用于DNN是一个有待讨论的优化问题。由于张量秩越低，我们将获得越高的压缩比，我们希望每一层DNN都可以通过非常低秩的张量分解来分解。然而，随着秩的降低，近似误差增加，导致精度的急剧损失。因此，在精度和压缩比之间存在折衷，这是一个广泛研究的问题。主要有三种低秩优化方法来实现良好的折衷：预训练方法、预设方法和压缩感知方法。

限于篇幅，未完待续。

1）预训练方法

2）预设方法

3）压缩感知方法

(三) 有效的稀疏度度量

三、与其他压缩技术相结合

四、子空间训练的低秩优化