【NLP】手把手使用PyTorch实现Transformer以及Transformer-XL
手把手使用PyTorch实现Transformer以及Transformer-XL
- Abstract of Attention is all you need
- 使用PyTorch实现Transformer
-
- 1. 构建Encoder-Decoder模型
-
- 1.1 导入依赖库
- 1.2 创建Encoder-Decoder类
- 1.3 创建Generator类
- 2. 构建Encoder
-
- 2.1 定义复制模块的函数
- 2.2 创建Encoder
- 2.3 构建LayerNorm
- 2.4 构建SublayerConnection
- 2.5 构建EncoderLayer
- 3. 构建Decoder
-
- 3.1 创建Decoder类
- 3.2 创建DecoderLayer类
- 3.3 定义subsequent_mask函数
- 4 构建MultiHeadedAttention
-
- 4.1 定义Attention
- 4.2 定义MultiHeadedAttention
- 5. 构建前馈网络层
- 6. 预处理输入数据
-
- 6.1 将输入数据转换成Embedding
- 6.2 添加位置编码
- 6.3 可视化位置编码
- 6.4 简单示例
- 7. 构建完整网络
- 8. 训练模型
-
- 8.1 定义Batch类
- 8.2 定义优化器类
- 8.3 定义正则化类
- 9. 实现一个简单实例
- Transformer-XL
-
- 引入循环机制
- 使用相对位置编码
- Transformer-XL计算过程
- 使用PyTorch构建Transformer-XL
- Reformer
-
- 使用局部敏感哈希
- 使用可逆残差网络
- 分块
- 总结
- 参考资料
Google 2017年的论文 Attention is all you need 提出了Transformer模型,完全基于Attention mechanism,抛弃了传统的RNN和CNN。本文根据论文的结构图,手把手带你使用 PyTorch 实现这个Transformer模型以及Transformer-XL模型。
Abstract of Attention is all you need
目前主要的序列转导模型基于复杂的循环神经网络或卷积神经网络,在编码器-解码器结构中进行配置。表现最佳的模型还通过注意机制将编码器和解码器连接起来。我们提出了一种新的简单网络架构,Transformer,仅基于注意机制,完全摒弃了循环和卷积。在两个机器翻译任务上的实验表明,这些模型在质量上优于其他模型,同时更易于并行化,并且训练时间显著缩短。我们的模型在WMT 2014年的英德翻译任务上实现了28.4的BLEU分数,相比现有最佳结果提高了2个BLEU分。在WMT 2014年的英法翻译任务中,我们的模型在8个GPU上训练3.5天后,取得了新的单模型BLEU分数纪录,达到了41.8,仅占据了文献中最佳模型训练成本的一小部分。我们展示了Transformer在其他任务中的泛化能力,成功地将其应用于英语成分解析,无论是在大量数据还是有限数据下。
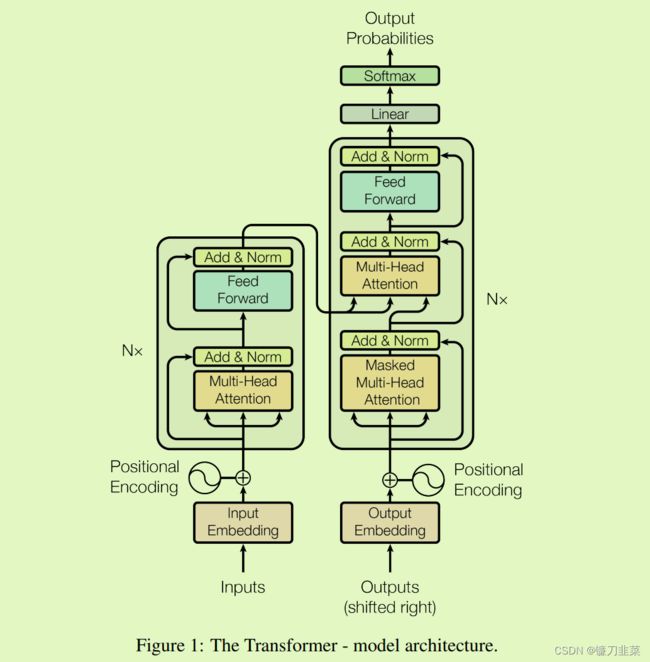
图1:Transformer模型架构图
基于上面论文中的Transformer模型架构图,经过梳理之后,得到如下概念图:

图2.Transformer模型实现的函数结构图
使用PyTorch实现Transformer
Encoder把输入序列 ( x 1 , . . . , x n ) (x_1, ...,x_n) (x1,...,xn)映射(或编码)成一个连续的序列 z = ( z 1 , . . . , z n ) z=(z_1,...,z_n) z=(z1,...,zn)。而Decoder根据 Z Z Z来解码得到输出序列 y 1 , . . . , y m y_1,...,y_m y1,...,ym。Decoder是自回归的(Auto-Regressive),会把前一个时刻的输出作为当前时刻的输入。Encoder-Decoder模型架构的代码分析如下:
1. 构建Encoder-Decoder模型
1.1 导入依赖库
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import math, copy, time
from torch.autograd import Variable
import matplotlib.pyplot as plt
import seaborn
seaborn.set_context(context='talk')
%matplotlib inline
1.2 创建Encoder-Decoder类
由于Transformer是一个Encoder-Decoder模型,因此,首先定义EncoderDecoder类,该类继承nn.Module。
class EncoderDecoder(nn.Module):
"""
这是一个标准的Encoder-Decoder模型
"""
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(EncoderDecoder, self).__init__()
# encoder和decoder都是构造的时候传入的,这样会非常灵活
self.encoder = encoder
self.decoder = decoder
# 输出和输出的embedding
self.src_embed = src_embed
self.tgt_embed = tgt_embed
# Decoder部分最后的Linear + softmax
self.generator = generator
def forward(self, src, tgt, src_mask, tgt_mask):
# 接收并处理屏蔽src和目标序列
# 首先调用encode方法对输入进行编码,然后调用decode方法进行编码
return self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)
def encode(self, src, src_mask):
# 传入参数包括src的embedding和src_mask
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
# 传入的参数包括目标embedding、Encoder的输出memory,及两种掩码
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
1.3 创建Generator类
Decoder的输出将传入一个全连接层,而后经过log_softmax函数的作用,成为概率值。
class Generator(nn.Module):
"""
定义标准的一个全连接(linear)+ softmax, 根据Decoder的隐状态输出一个词
d_model是Decoder输出的大小,vocab是词典大小
"""
def __init__(self, d_model, vocab):
super(Generator, self).__init__()
self.proj = nn.Linear(d_model, vocab)
# 全连接再加上一个softmax
def forward(self, x):
return F.log_softmax(self.proj(x), dim=-1)
2. 构建Encoder
Encoder由N个相同结构的EncoderLayer堆积(stack)而成,而每个Encoder层又有两个子层。第一个是一种多头部的自注意力机制,第二个是按位置全连接的前馈网络。其间还有LayerNorm及残差连接等。
2.1 定义复制模块的函数
定义clone函数,用于克隆相同的Encoder层:
def clones(module, N):
"""克隆N个完全相同的子层,使用了copy.deepcopy"""
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
这里使用了nn.ModuleList。ModuleList就像一个普通的Python的List,使用下标来访问它,而且传入的ModuleList的所有Module都会注册到PyTorch里,这样Optimizer就能找到其中的参数,从而用梯度下降进行更新。但是nn.ModuleList并不是Module(的子类),因此它没有forward等方法,通常会被放到某个Module里。
2.2 创建Encoder
创建Encoder,代码如下:
class Encoder(nn.Module):
"""Encoder是N个EncoderLayer的堆积而成"""
def __init__(self, layer, N):
super(Encoder, self).__init__()
# layer是一个SubLayer,我们clone N个
self.layers = clones(layer, N)
# 再加一个LayerNorm层
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
"把输入(x, mask)被逐层处理"
for layer in self.layers:
x = layer(x, mask)
return self.norm(x) # N个EncoderLayer处理完成之后还需要一个LayerNorm
根据上面代码可知,Encoder就是由N个子层组成的栈,最后加上一个LayerNorm。
2.3 构建LayerNorm
构建LayerNorm模型,代码如下:
class LayerNorm(nn.Module):
"构建一个LayerNorm模块"
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
具体处理过程为:
x -> x + self-attention(x) -> layernorm(x+self-attention(x)) => y
y -> dense(y) -> y+dense(y) -> layernorm(y+dense(y)) => z(输入下一层)
这里把Layernorm层放到前面了,即处理过程如下:
x -> layernorm(x) -> self-attention(layernorm) -> x+self-attention(layernorm(x))
y -> layernorm(y) -> dense(layernorm(y)) -> y+dense(layernorm(y)) -> z(输入下一层)
PyTorch中各层权重的数据类型是nn.Parameter,而不是Tensor。故需要对初始化后的参数(Tensor型)进行类型转换。**每个Encoder层又有两个子层,每个子层通过残差把每层的输入转换为新的输出。不管是自注意力层还是全连接层,都先是LayerNorm,然后是Self-Attention/Dense,接着是Dropout层,最后是残差连接层。**接下来把它们封装成SublayerConnection。
2.4 构建SublayerConnection
构建SublayerConnection模型,代码如下:
class SublayerConnection(nn.Module):
"""LayerNorm + sublayer(Self-Attention/Dense) + dropout + 残差连接
为了简单,把LayerNorm放到了前面,这和原始论文稍有不同,原理论文LayerNorm在最后
"""
def __init__(self, size, dropout):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self, x, sublayer):
# 将残差连接应用于具有相同大小的任何子层
return x + self.dropout(sublayer(self.norm(x)))
2.5 构建EncoderLayer
有了以上代码,就可以构建EncoderLayer了,代码如下:
class EncoderLayer(nn.Module):
"Encoder由self_attn和feed_forward构建"
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size
def forward(self, x, mask):
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feed_forward)
为了增加复用性,把self_attn层和feed_forward层作为参数传入,只构造两个子层。forward调用sublayer[0](这是sublayer对象),最终会调到它的forward方法,而这个方法需要两个参数,一个是输入Tensor,另一个是对象或函数。在Python中,类似的实例可以像函数一样,可以被调用。而self_attn函数需要4个参数,即query的输入、key的输入、value的输入和mask,因此,使用lambda的技巧是把它变成一个参数x的函数(mask可以看成已知的数)。
3. 构建Decoder
前面提到,Decoder也是由N个Decoder层堆叠而成,参数layer是Decoder层数,它也是一个调用对象,最终会调用DecoderLayer.forward方法,这个方法需要4个参数:输入x、Encoder层的输出memory、输入Encoder的mask(src_mask)和输入Decoder的mask(tgt_mask)。所有这里的Decoder的forward方法也需要这4个参数。
3.1 创建Decoder类
class Decoder(nn.Module):
"构建N个完全相同的Decoder层"
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)
3.2 创建DecoderLayer类
class DecoderLayer(nn.Module):
"Decoder包括self_attn, src_attn和feed_forward层"
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3)
def forward(self, x, memory, src_mask, tgt_mask):
m = memory
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
return self.sublayer[2](x, self.feed_forward)
由代码可知,DecoderLayer类比EncoderLayer类多一个src_attn层,这是解码器关注编码器的输出(memory)。src-attn和self-attn的实现是一样的,只是query、key和value的输入不同。普通注意力(src-attn)的query来自下层的输入(即self-attn的输出),key和value来自Encoder最后一层的输出memory;而Self-Attention的query、key和value都是来自下层的输入。
3.3 定义subsequent_mask函数
Decoder和Encoder有一个关键的不同:Decoder在解码第t个时刻的时候只能使用 1... t 1...t 1...t时刻的输入,而不能使用 t + 1 t+1 t+1时刻及其之后的输入。因此需要一个函数来生成一个Mask矩阵,代码如下:
def subsequent_mask(size):
"Mask out subsequent positions."
attn_shape = (1, size, size)
subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
return torch.from_numpy(subsequent_mask) == 0
4 构建MultiHeadedAttention
4.1 定义Attention
Attention(包括Self-Attention和普通的Attention)可以看作一个函数,它的输入是query、key、value和mask,输出是一个张量(Tensor)。其中输出是value的加权平均,而权重由query和key计算得出。具体的计算公式如下: A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V
def attention(query, key, value, mask=None, dropout=None):
"计算 'Scaled Dot-Product Attention'"
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2,-1))/math.sqrt(d_k)
if mask is not None:
scores = scores.masked_fill(mask==0, -1e-9)
p_attn = F.softmax(scores, dim = -1)
if dropout is not None:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
代码实现中, Q K T d k \frac{QK^T}{\sqrt{d_k}} dkQKT和公式里的稍微不同,这里的 Q Q Q和 K K K都是4维张量,包括batch和head维度。torch.matmul会对query和key的最后两维进行矩阵乘法,这样效率更高,如果用标准的矩阵(2维张量)乘法来实现,则需要遍历batch维度和head维度。
4.2 定义MultiHeadedAttention
对于每一个head,都使用三个矩阵 w Q 、 w K 、 w V w^Q、w^K、w^V wQ、wK、wV把输入转换成Q、K和V,然后分别用每一个head进行自注意力计算,把N个head的输出拼接起来,与矩阵 w O w^O wO相乘。MultiHeadedAttention的公式如下: M u l t i H e a d ( Q , K , V ) = c o n c a t ( h e a d 1 , h e a d 2 , . . . , h e a d h ) W O MultiHead(Q,K,V)=concat(head_1, head_2, ..., head_h)W^O MultiHead(Q,K,V)=concat(head1,head2,...,headh)WO
h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) head_i=Attention(QW_i^Q, KW_i^K, VW_i^V) headi=Attention(QWiQ,KWiK,VWiV)
这里映射是参数矩阵,其中 W i Q ∈ R d m o d e l d q W_i^Q\in R^{d_{model}d_q} WiQ∈Rdmodeldq, W i K ∈ R d m o d e l d k W_i^K\in R^{d_{model}d_k} WiK∈Rdmodeldk, W i V ∈ R d m o d e l d v W_i^V\in R^{d_{model}d_v} WiV∈Rdmodeldv, W i O ∈ R h d v d m o d e l W_i^O\in R^{hd_vd_{model}} WiO∈Rhdvdmodel。
假设head个数为8,即 h = 8 h=8 h=8, d k = d v = d m o d e l h = 64 d_k=d_v=\frac{d_{model}}{h}=64 dk=dv=hdmodel=64。代码如下:
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1):
"传入head个数及model的维度"
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# 这里假设d_v=d_k
self.d_k = d_model // h
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
if mask is not None:
# 相同的mask适应所有的head
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1)首先使用线性变换,然后把d_model分配给h个Head,每个head为d_k=d_model/h
query, key, value = [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1,2) for l, x in zip(self.linears, (query, key, value))]
# 2)使用attention函数计算缩放点积注意力
x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)
# 3)实现Multi-head attention,用view函数把8个head的64维向量拼接成一个512的向量。
# 然后再使用一个线性变换(512, 512), shape不变
x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x)
其中zip(self.linears, (query, key, value))是把(self.linears[0], self.linears[1], self.linears[2])和(query, key, value)放到一起遍历。这里我们只看一个self.linears[0](query)。根据构造函数的定义,self.linears[0]是一个(512,512)的矩阵,而query是(batch, time, 512),相乘之后得到的新query还是512(d_model)维的向量,然后用view函数把它变成(batch, time, 8, 64)。接着转换成(batch, 8, time, 64),这是attention函数要求的shape。分别对应8个head,每个head的query都是64维。
key和value的运算完全相同,因此我们也分别得到8个head的64维的key和64维的value。然后调用attention函数,得到x和self.attn。其中x的shape是(batch, 8, time, 64),而attn是(batch, 8, time, time),x.transpose(1,2)把x变成(batch, time, 8, 64),然后用view函数把它变成(batch, time, 512),也就是把最后8个64维的向量拼接成512的向量。最后使用self.linears[-1]对x进行线性变换,self.linears[-1]是(512,512)的,因此最终的输出还是(batch, time, 512)。
我们最初构造了4个(512, 512)的矩阵,前3个矩阵用于对query、key和value进行变换,最后一个矩阵对8个head拼接后的向量再做一次变换。
MultiHeadedAttention的应用主要有以下几种:
- Encoder的自注意力层。query、key和value都是相同的值,来自下层的输入,Mask都是1(当然padding的不算)。
- Decoder的自注意力层。query、key和value都是相同的值,来自下层的输入,但是Mask使得它不能访问未来的输入。
- Encoder-Decoder的普通注意力层。query来自下层的输入,key和value相同,是Encoder最后一层的输出,而Mask都是1.
5. 构建前馈网络层
除了需要注意子层之外,还需要注意编码器和解码器中的每个层都包含一个完全连接的前馈网络。该网络应用于每层的对应位置。这包括两个线性转换,中间有一个ReLU激活函数,具体公式为: F F N ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN(x)=max(0, xW_1+b_1)W_2+b_2 FFN(x)=max(0,xW1+b1)W2+b2
全连接层的输入和输出的d_model都是512,中间隐单元的个数d_ff为2048,具体代码如下:
class PositionwiseFeedForward(nn.Module):
"实现FFN函数"
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.w_2(self.dropout(F.relu(self.w_1(x))))
6. 预处理输入数据
输入的词序列都是ID序列,所以需要对其进行预处理。源语言和目标语言都需要嵌入,此外我们还需要一个线性变换把隐变量变成输出概率,这可以通过前面的Generator类来实现。
Transformer模型的注意力机制并没有包含位置信息,也就是说,即使一句话中词语在不同的位置,但其在Transformer中是没有区别的,这显然不符合实际。因此,在Transformer中引入位置信息对于CNN、RNN等模型有非常重要的作用。
作者添加位置编码的方法是:构造一个跟输入嵌入维度一样的矩阵,然后跟输入嵌入相加得到多头注意力的输入。
6.1 将输入数据转换成Embedding
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
#d_model=512, vocab=当前语言的词表大小
super(Embeddings, self).__init__()
self.lut = nn.Embedding(vocab, d_model)
# one-hot转词嵌入,这里有一个待训练的矩阵E,大小是vocab*d_model
self.d_model = d_model
def forward(self, x):
# x ~ (batch.size, sequence.length, one-hot),
#one-hot大小=vocab,当前语言的词表大小
return self.lut(x) * math.sqrt(self.d_model)
# 得到的10*512词嵌入矩阵,主动乘以sqrt(512)=22.6,
6.2 添加位置编码
位置编码的公式如下: P E ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i / d m o d e l ) PE(pos, 2i)=sin(pos/10000^{2i/d_{model}}) PE(pos,2i)=sin(pos/100002i/dmodel) P E ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i / d m o d e l ) PE(pos, 2i+1)=cos(pos/10000^{2i/d_{model}}) PE(pos,2i+1)=cos(pos/100002i/dmodel)
代码如下:
class PositionalEncoding(nn.Module):
"实现PE函数"
def __init__(self, d_model, dropout, max_len=5000):
#d_model=512,dropout=0.1,
#max_len=5000代表事先准备好长度为5000的序列的位置编码,其实没必要,一般100或者200足够了。
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
#Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model)
#(5000,512)矩阵,保持每个位置的位置编码,一共5000个位置,每个位置用一个512维度向量来表示其位置编码
position = torch.arange(0, max_len).unsqueeze(1)
# (5000) -> (5000,1)
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0)/d_model))
pe[:, 0::2] = torch.sin(position * div_term) # 偶数下标的位置
pe[:, 1::2] = torch.cos(position * div_term) # 奇数下标的位置
pe = pe.unsqueeze(0)
# (5000, 512) -> (1, 5000, 512) 为batch.size留出位置
self.register_buffer('pe', pe)
def forward(self, x):
x = x + self.pe[:, :x.size(1)].clone().detach()
return self.dropout(x)
这里调用了Module.register_buffer函数。该函数的作用是创建一个buffer缓冲区,比如这里把pe保存下来。register_buffer通常用于保存一些模型参数之外的值,比如在BatchNorm中,需要保存running_mean(平均位移),它不是模型的参数(不是通过迭代学习的参数),但是模型会修改它,而且在预测的时候也要用到它。这里也是类似的,pe是一个提前计算好的常量,在forward函数会经常用到。在构造函数里并没有把pe保存到self参数里,但是forward函数调用时却可以直接使用它(self.pe)。如果保存(序列化)模型到磁盘,则PyTorch框架将把缓冲区里的数据保存到磁盘,这样反序列化的时候才能恢复它们。
6.3 可视化位置编码
假设输入是长度为10的ID序列,如果输入E吗bedding之后是(10, 512),那么位置编码的输出也是(10,512)。对应pos就是位置(0~9), 512维的偶数维使用sin函数,奇数维使用cos函数。这种位置编码的好处是:PEpos+k可以表示成PEpos的线性函数,这样前馈网络就能很容易地学习到相对位置的关系。
## 语句长度维100, 这里假设d_model=20
plt.figure(figsize=(15, 5))
pe = PositionalEncoding(20, 0)
y = pe.forward(torch.zeros(1, 100, 20))
plt.plot(np.arange(100), y[0,:,4:8].data.numpy())
plt.legend(["dim %d"%p for p in [4,5,6,7]])
6.4 简单示例
生成位置编码的简单示例如下:
d_model, dropout, max_len = 512, 0, 5000
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0)/d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
print(pe.shape)
pe = pe.unsqueeze(0)
print(pe.shape)
torch.Size([5000, 512])
torch.Size([1, 5000, 512])
7. 构建完整网络
把前面创建的各网络层整合成一个完整网络:
def make_model(src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h=8, dropout=0.1):
"构建模型"
c = copy.deepcopy
attn = MultiHeadedAttention(h, d_model)
ff = PositionwiseFeedForward(d_model, d_ff, dropout)
position = PositionalEncoding(d_model, dropout)
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
Generator(d_model, tgt_vocab)
)
# 随机初始化参数,非常重要,这里使用Glorot/fan_avg
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
return model
首先把copy.deepcopy命名为c。然后构造MultiHeadedAttention、PositionwiseFeedForward和PositionalEncoding对象,接着构造Encoder和Decoder对象,该对象需要5个参数:Encoder、Decoder、src_embed、tgt_embed和Generator。
先看后面三个简单的参数:Generator可以直接构造,它的作用是把模型的隐单元变成输出词的概率;而src_embed是一个嵌入层和一个位置编码层c;tgt_embed与之类似。
最后来看Decoder(Encoder和Decoder类似)。Decoder由N个DecoderLayer组成,而DecoderLayer需要传入self-attn、src-attn、连接层和Dropout层。因为所有的MultiHeadedAttention都是一样的,因此直接深度复制(deepcopy)就行;同理,所有的PositionwiseFeedForward也是一样的。
实例化这个类,可以看到模型包含哪些组件:
# 测试一个简单模型,输入、目标语句长度分别为10、Encoder、Decoder各2层。
tmp_model = make_model(10, 10, 2)
tmp_model
输出结果:
EncoderDecoder(
(encoder): Encoder(
(layers): ModuleList(
(0-1): 2 x EncoderLayer(
(self_attn): MultiHeadedAttention(
(linears): ModuleList(
(0-3): 4 x Linear(in_features=512, out_features=512, bias=True)
)
(dropout): Dropout(p=0.1, inplace=False)
)
(feed_forward): PositionwiseFeedForward(
(w_1): Linear(in_features=512, out_features=2048, bias=True)
(w_2): Linear(in_features=2048, out_features=512, bias=True)
(dropout): Dropout(p=0.1, inplace=False)
)
(sublayer): ModuleList(
(0-1): 2 x SublayerConnection(
(norm): LayerNorm()
(dropout): Dropout(p=0.1, inplace=False)
)
)
)
)
(norm): LayerNorm()
)
(decoder): Decoder(
(layers): ModuleList(
(0-1): 2 x DecoderLayer(
(self_attn): MultiHeadedAttention(
(linears): ModuleList(
(0-3): 4 x Linear(in_features=512, out_features=512, bias=True)
)
(dropout): Dropout(p=0.1, inplace=False)
)
(src_attn): MultiHeadedAttention(
(linears): ModuleList(
(0-3): 4 x Linear(in_features=512, out_features=512, bias=True)
)
(dropout): Dropout(p=0.1, inplace=False)
)
(feed_forward): PositionwiseFeedForward(
(w_1): Linear(in_features=512, out_features=2048, bias=True)
(w_2): Linear(in_features=2048, out_features=512, bias=True)
(dropout): Dropout(p=0.1, inplace=False)
)
(sublayer): ModuleList(
(0-2): 3 x SublayerConnection(
(norm): LayerNorm()
(dropout): Dropout(p=0.1, inplace=False)
)
)
)
)
(norm): LayerNorm()
)
(src_embed): Sequential(
(0): Embeddings(
(lut): Embedding(10, 512)
)
(1): PositionalEncoding(
(dropout): Dropout(p=0.1, inplace=False)
)
)
(tgt_embed): Sequential(
(0): Embeddings(
(lut): Embedding(10, 512)
)
(1): PositionalEncoding(
(dropout): Dropout(p=0.1, inplace=False)
)
)
(generator): Generator(
(proj): Linear(in_features=512, out_features=10, bias=True)
)
)
8. 训练模型
8.1 定义Batch类
1)训练前,首先介绍一个便于批次训练的Batch类:
class Batch:
"在训练起见,构建带有掩码的批量数据"
def __init__(self, src, trg=None, pad=0):
# src: 源语言序列,(batch.size, src.seq.len) 二维tensor,第一维度是batch.size;第二个维度是源语言句子的长度
# 例如:[ [2,1,3,4], [2,3,1,4] ]这样的二行四列的,1-4代表每个单词word的id
# trg: 目标语言序列,默认为空,其shape和src类似,(batch.size, trg.seq.len),
# 二维tensor,第一维度是batch.size;第二个维度是目标语言句子的长度
# 例如trg=[ [2,1,3,4], [2,3,1,4] ] for a "copy network" (输出序列和输入序列完全相同)
# pad: 源语言和目标语言统一使用的 位置填充符号,'', 所对应的id,这里默认为0
# 例如,如果一个source sequence,长度不到4,则在右边补0: [1,2] -> [1,2,0,0]
self.src = src
self.src_mask = (src != pad).unsqueeze(-2)
# src = (batch.size, seq.len) -> != pad ->
# (batch.size, seq.len) -> usnqueeze ->
# (batch.size, 1, seq.len) 相当于在倒数第二个维度扩展
# e.g., src=[ [2,1,3,4], [2,3,1,4] ] 对应的是 src_mask=[ [[1,1,1,1], [1,1,1,1]] ]
if trg is not None:
self.trg = trg[:, :-1] # 重要
# trg 相当于目标序列的前N-1个单词的序列(去掉了最后一个词)
self.trg_mask = trg[:, 1:]
# trg_y 相当于目标序列的后N-1个单词的序列(去掉了第一个词)
# 目的是(src + trg) 来预测出来(trg_y),
self.trg_mask = self.make_std_mask(self.trg, pad)
self.ntokens = (self.trg_y != pad).data.sum()
@staticmethod
def make_std_mask(tgt, pad):
"Create a mask to hide padding and future words."
# 这里的tgt类似于:[ [2,1,3], [2,3,1] ] (最初的输入目标序列,分别去掉了最后一个词
# pad=0, ''的id编号
tgt_mask = (tgt != pad).unsqueeze(-2)
# 得到的tgt_mask类似于tgt_mask = tensor([[[1, 1, 1]],[[1, 1, 1]]], dtype=torch.uint8)
# shape=(2,1,3)
# tgt_mask = tgt_mask & subsequent_mask(tgt.size(-1)).type_as(tgt_mask.data).clone().detach()
tgt_mask = tgt_mask & Variable(subsequent_mask(tgt.size(-1)).type_as(tgt_mask.data))
# 先看subsequent_mask, 其输入的是tgt.size(-1)=3,这个函数的输出为= tensor([[[1, 0, 0],[1, 1, 0],[1, 1, 1]]], dtype=torch.uint8)
# type_as 把这个tensor转成tgt_mask.data的type(也是torch.uint8)
# 这样的话,&的两边的tensor分别是(2,1,3), (1,3,3);
# tgt_mask = tensor([[[1, 1, 1]],[[1, 1, 1]]], dtype=torch.uint8)
# and
# tensor([[[1, 0, 0], [1, 1, 0], [1, 1, 1]]], dtype=torch.uint8)
# (2,3,3)就是得到的tensor
# tgt_mask.data = tensor([[[1, 0, 0],[1, 1, 0],[1, 1, 1]], [[1, 0, 0],[1, 1, 0],[1, 1, 1]]], dtype=torch.uint8)
return tgt_mask
Batch构造函数的输入是src、trg和pad,其中trg的默认值为None。刚预测的时候是没有tgt的。为了便于理解,这里举一个例子。假设这是训练阶段的一个Batch,src的维度为(40, 20),其中40是批量大小,20是最长的句子长度,其他不够长的都填充成20。而trg的维度为(40, 25),表示翻译后的最长句子是25个单词,不足的也已填充对齐。
那么src_mask要如何实现呢?注意,表达式(src != pad)是指把src中大于0的时刻置为1,以表示它已在关注的范围内。然后unsqueeze(-2)把src_mask变成(40/batch, 1, 20/time)。它的用法可以参考前面的attention函数。
注意,src_mask的shape是(batch, 1, time),而trg_mask是(batch, time, time)。这是因为src_mask的每一个时刻都能关注所有时刻(填充的时间除外),一次只需要一个向量就行了,而trg_mask需要一个矩阵。
8.2 定义优化器类
2)定义优化器,这里使用Adam算法
class NoamOpt:
"包括优化学习率的优化器."
def __init__(self, model_size, factor, warmup, optimizer):
self.optimizer = optimizer
# optimizer = Adam (Parameter Group 0
# amsgrad: False
# betas: (0.9, 0.98)
# eps: 1e-09
# lr: 0
# weight_decay: 0
#)
self._step = 0
self.warmup = warmup
self.factor = factor
self.model_size = model_size
self._rate = 0
def step(self):
"更新参数及学习率"
self._step += 1
rate = self.rate()
for p in self.optimizer.param_groups:
p['lr'] = rate
self._rate = rate
self.optimizer.step()
def rate(self, step = None):
"Implement `lrate`(learning rate) above"
if step is None:
step = self._step
return self.factor * (self.model_size ** (-0.5) * min(step ** (-0.5), step * self.warmup ** (-1.5)))
def get_std_opt(model):
return NoamOpt(model.src_embed[0].d_model, 2, 4000, torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
下面是学习率在不同场景下的变化情况
# 超参数学习率的3个场景
opts = [NoamOpt(512, 1, 4000, None), NoamOpt(512, 1, 8000, None), NoamOpt(256, 1, 4000, None)]
plt.plot(np.arange(1, 20000), [[opt.rate(i) for opt in opts] for i in range(1, 20000)])
plt.legend(["512:4000", "512:8000", "256:4000"])
plt.xlabel('iterations')
plt.ylabel('learning rate')
8.3 定义正则化类
3)对标签做正则化平滑处理,可以提高模型的准确性和BLEU分数,简单思想就是劫富济贫。代码如下:
class LabelSmoothing(nn.Module):
"Implement label smoothing."
def __init__(self, size, padding_idx, smoothing=0.0):
super(LabelSmoothing, self).__init__()
self.criterion = nn.KLDivLoss(size_average=False)
self.padding_idx = padding_idx # '' 的id
self.confidence = 1.0 - smoothing # 自留的概率值、得分 e.g. 0.6
self.smoothing = smoothing # 均分出去的概率值,得分 e.g. 0.4
self.size = size # target vocab size 目标语言词表大小
self.true_dist = None
def forward(self, x, target):
"in real-world case: 真实情况下"
# x的shape为(batch.size * seq.len, target.vocab.size), y的shape是(batch.size * seq.len)
# x = logits,(seq.len, target.vocab.size)
# 每一行,代表一个位置的词
# 类似于:假设seq.len=3, target.vocab.size=5
# x中保存的是log(prob)
# x = tensor([[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
# [-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
# [-20.7233, -1.6094, -0.3567, -2.3026, -20.7233]])
# target 类似于:target = tensor([2, 1, 0]),torch.size=(3)
assert x.size(1) == self.size # 目标语言词表大小
true_dist = x.data.clone()
# true_dist = tensor([[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
# [-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
# [-20.7233, -1.6094, -0.3567, -2.3026, -20.7233]])
true_dist.fill_(self.smoothing / (self.size - 2))
# true_dist = tensor([[0.1333, 0.1333, 0.1333, 0.1333, 0.1333],
# [0.1333, 0.1333, 0.1333, 0.1333, 0.1333],
# [0.1333, 0.1333, 0.1333, 0.1333, 0.1333]])
# 注意,这里分母target.vocab.size-2是因为(1)最优值0.6要占一个位置;(2)填充词要被排除在外
# 所以被激活的目标语言词表大小就是self.size-2
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
# target.data.unsqueeze(1) -> tensor([[2],[1],[0]]); shape=torch.Size([3, 1])
# self.confidence = 0.6
# 根据target.data的指示,按照列优先(1)的原则,把0.6这个值填入true_dist:
# 因为target.data是2,1,0的内容,所以,0.6填入第0行的第2列(列号,行号都是0开始)->0.6填入第1行的第1列->0.6填入第2行的第0列:
# true_dist = tensor([[0.1333, 0.1333, 0.6000, 0.1333, 0.1333],
# [0.1333, 0.6000, 0.1333, 0.1333, 0.1333],
# [0.6000, 0.1333, 0.1333, 0.1333, 0.1333]])
true_dist[:, self.padding_idx] = 0
# true_dist = tensor([[0.0000, 0.1333, 0.6000, 0.1333, 0.1333],
# [0.0000, 0.6000, 0.1333, 0.1333, 0.1333],
# [0.0000, 0.1333, 0.1333, 0.1333, 0.1333]])
# 设置true_dist这个tensor的第一列的值全为0,因为这个是填充词''所在的id位置,不应该计入目标词表。
# 需要注意的是,true_dist的每一列,代表目标语言词表中的一个词的id
mask = torch.nonzero(target.data == self.padding_idx)
# mask = tensor([[2]]), 也就是说,最后一个词 2,1,0中的0,因为是''的id,所以通过上面的一步,把他们找出来
if mask.dim() > 0:
true_dist.index_fill_(0, mask.squeeze(), 0.0)
# 当target reference序列中有0这个''的时候,则需要把这一行的值都清空。
# 在一个batch里面的时候,可能两个序列长度不一,所以短的序列需要pad ''来填充,所以会出现类似于(2,1,0)这样的情况
# true_dist = tensor([[0.0000, 0.1333, 0.6000, 0.1333, 0.1333],
# [0.0000, 0.6000, 0.1333, 0.1333, 0.1333],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000]])
self.true_dist = true_dist
# return self.criterion(x, true_dist.clone().detach())
return self.criterion(x, Variable(true_dist, requires_grad=False))
# 这一步就是调用KL loss来计算
# x = tensor([[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
# [-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
# [-20.7233, -1.6094, -0.3567, -2.3026, -20.7233]])
# true_dist=tensor([[0.0000, 0.1333, 0.6000, 0.1333, 0.1333],
# [0.0000, 0.6000, 0.1333, 0.1333, 0.1333],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000]])
# 之间的loss。
这里先定义实现标签平滑处理的类,该类使用KL散度损失(nn.KLDivLoss)实现标签平滑。创建一个分布,该分布具有对正确单词的置信度,而其余平滑质量分布的整个词汇表中。
举个简单的例子:
crit = LabelSmoothing(5, 0, 0.4) # trg.vocab.size=5, pad_idx=0, smooth=0.4 and thus confidence=0.6
predict = torch.FloatTensor([[0, 0.2, 0.7, 0.1, 0], [0, 0.2, 0.7, 0.1, 0], [0, 0.2, 0.7, 0.1, 0]])
# predicted logits tensor
"smooth only and important"
predict = predict.masked_fill(predict == 0, 1e-9) # "smooth only"
v = crit(Variable(predict.log()), Variable(torch.LongTensor([2, 1, 0])))
plt.imshow(crit.true_dist)

上图中,第0列,都是0,代表了’
这个类LabelSmoothing,一方面对label进行平滑,如果Model对于一个结果非常确信,则loss反而惩罚它(貌似缺少了多样性);另外一方面则是对loss进行计算的。
BLEU分数:Bilingual Evaluation Understudy,双倍评估替换分数,常用于说明候选文本与参考文本的相似程度,值越接近1,说明两个文本越相似。
9. 实现一个简单实例
下面通过一个简单的例子来整体串一下transformer:
1)生成合成数据
假设我们的目的是构建一个copy network,输入和输出完全一致:
# 生成合成数据
def data_gen(V, batch, nbatches):
"Generate random data for a src-tgt copy task."
for i in range(nbatches):
# 把torch.Embedding的输入类型改为LongTensor
data = torch.from_numpy(np.random.randint(1, V, size=(batch, 10))).long()
data[:, 0] = 1
src = data.clone().detach()
tgt = data.clone().detach()
yield Batch(src, tgt, 0)
假设batch.size=2, source.vocab.size=4=target.vocab.size.
2)定义损失函数
封装的基于batch来计算loss的类:
# 定义损失函数
class SimpleLossCompute:
"一个简单的计算损失的函数"
def __init__(self, generator, criterion, opt=None):
self.generator = generator # Generator 对象, linear+softmax
self.criterion = criterion # LabelSmooth对象,计算loss
self.opt = opt # NormOpt对象,优化算法对象
def __call__(self, x, y, norm):
# e.g., x为(2,3,8), batch.size=2, seq.len=3, d_model=8
# y = tensor([[4, 2, 1], [4, 4, 4]], dtype=torch.int32)
# norm: (y=trg_y中非''的token的个数)
"attention here"
x = self.generator(x)
loss = self.criterion(x.contiguous().view(-1, x.size(-1)), y.contiguous().view(-1)) / norm.item()
# 变形后,x类似于(batch.size*seq.len, target.vocab.size) y为(target.vocab.size)
# 然后调用LabelSmooth来计算loss
loss.backward()
if self.opt is not None:
self.opt.step()
self.opt.optimizer.zero_grad()
#return loss.data[0] * norm
return loss.item() * norm.item()
- 构建训练迭代函数
下面看一个相对完整的训练loop:
# 构建训练迭代函数
def run_epoch(data_iter, model, loss_compute):
"Standard Training and Logging Function"
# data_iter = 所有数据的打包
# model = EncoderDecoder 对象
# loss_compute = SimpleLossCompute对象
start = time.time()
total_tokens = 0
total_loss = 0
tokens = 0
for i, batch in enumerate(data_iter):
# 对每个batch循环
out = model.forward(batch.src, batch.trg, batch.src_mask, batch.trg_mask)
# 使用目前的model,对batch.src+batch.trg进行forward
loss = loss_compute(out, batch.trg_y, batch.ntokens)
total_loss += loss
total_tokens += batch.ntokens
tokens += batch.ntokens
if i % 50 == 1:
elapsed = time.time() - start
print('epoch step: {} Loss: {}/{}, tokens per sec: {}/{}'.format(i, loss, batch.ntokens, tokens, elapsed))
start = time.time()
tokens = 0
return total_loss / total_tokens
它遍历epoch(epoch指整个训练集被训练的次数)次数据,然后调用forward函数,接着用loss_compute函数计算梯度,更新参数并返回loss。
4) 对数据进行批量处理
# 对数据进行批量处理
global max_src_in_batch, max_tgt_in_batch
def batch_size_fn(new, count, sofar):
"Keep augmenting batch and calculate total number of tokens + padding"
global max_src_in_batch, max_tgt_in_batch
if count == 1:
max_src_in_batch = 0
max_tgt_in_batch = 0
max_src_in_batch = max(max_src_in_batch, len(new.src))
max_tgt_in_batch = max(max_tgt_in_batch, len(new.trg) + 2)
src_elements = count * max_src_in_batch
tgt_elements = count * max_tgt_in_batch
return max(src_elements, tgt_elements)
5)训练简单任务
# 训练简单任务
# Train the simple copy task.
V = 5 # here V is the vocab size of source and target languages (sequences)
criterion = LabelSmoothing(size=V, padding_idx=0, smoothing=0.01) # 创建损失函数计算对象
model = make_model(V, V, N=2, d_model=8, d_ff=16, h=2)
# EncoderDecoder对象构造
'''
in make_model: src_vocab_size=11, tgt_vocab_size=11, N=2, d_model=512, d_ff=2048, h=8, dropout=0.1
'''
model_opt = NoamOpt(model.src_embed[0].d_model, 1, 400, torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
lossfun = SimpleLossCompute(model.generator, criterion, model_opt)
for epoch in range(10):
model.train()
run_epoch(data_gen(V, 30, 20), model, SimpleLossCompute(model.generator, criterion, model_opt))
model.eval()
print(run_epoch(data_gen(V, 30, 5), model, SimpleLossCompute(model.generator, criterion, None)))
运行结果:

6)贪心解码算法(只看top-1的结果)
为了简单起见,使用贪婪解码来预测翻译结果
# 使用贪婪解码算法
def greedy_decode(model, src, src_mask, max_len, start_symbol):
memory = model.encode(src, src_mask)
# 源语言的一个batch执行encode编码工作,得到memory
# shape=(batch.size, src.seq.len, d_model)
# src = (1,4), batch.size=1, seq.len=4
# src_mask = (1,1,4) with all ones
# start_symbol=1
print('memory={}, memory.shape={}'.format(memory, memory.shape))
ys = torch.ones(1, 1).fill_(start_symbol).type_as(src.data)
# 最初ys=[[1]], size=(1,1); 这里start_symbol=1
print('ys={}, ys.shape={}'.format(ys, ys.shape))
for i in range(max_len-1): # max_len = 5
out = model.decode(memory, src_mask, ys, subsequent_mask(torch.tensor(ys.size(1)).type_as(src.data)))
# memory, (1, 4, 8), 1=batch.size, 4=src.seq.len, 8=d_model
# src_mask = (1,1,4) with all ones
# out, (1, 1, 8), 1=batch.size, 1=seq.len, 8=d_model
prob = model.generator(out[:, -1])
_, next_word = torch.max(prob, dim=1)
next_word = next_word.data[0]
# word id of "next_word"
ys = torch.cat([ys, torch.ones(1,1).type_as(src.data).fill_(next_word)], dim=1)
# ys is in shape of (1,2) now, i.e., 2 words in current seq
return ys
model.eval()
src = torch.LongTensor([[1, 2, 3, 4]])
src_mask = Variable(torch.ones(1, 1, 4))
print(greedy_decode(model, src, src_mask, max_len=7, start_symbol=1))
Transformer-XL
Transformer使用自注意力机制,可以让单词之间直接建立联系,因此Transformer编码信息和学习特征的能力比RNN强。但是Transformer 本身是不能利用单词的顺序信息的,因此需要在输入中添加位置 Embedding,否则 Transformer 就是一个词袋模型了。
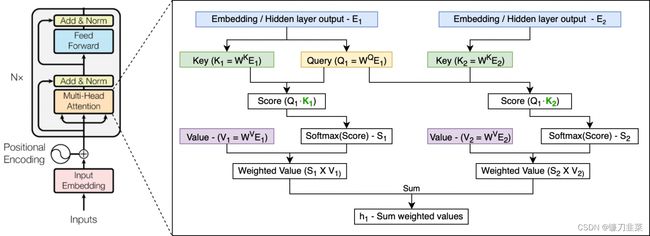
Transformer中编码器部分的结构图。
Transformer的问题:
- 长句子切割造成语义的残破,不利于模型的训练
- 片段的切割没有考虑语义,也就是模型在训练当前片段时拿不到前面时刻片段的信息,造成语义的分隔。
为了解决这些问题,提出了Transformer-XL。利用Transformer-XL可以提高vanilla Transformer学习长期依赖信息的能力。为何要提这个模型?因为Transformer-XL是基于这个模型进行的改进。
Al-Rfou等人基于Transformer提出了一种训练语言模型的方法( https://arxiv.org/abs/1808.04444 ),来根据之前的字符预测片段中的下一个字符。例如,它使用 x 1 , x 2 , . . . , x n − 1 x_1, x_2, ..., x_{n-1} x1,x2,...,xn−1预测字符 x n x_n xn,而在 x n x_n xn之后的序列则被mask掉。论文中使用64层模型,并仅限于处理 512个字符这种相对较短的输入,因此它将输入分成段,并分别从每个段中进行学习,如下图所示。 在测试阶段如需处理较长的输入,该模型会在每一步中将输入向右移动一个字符,以此实现对单个字符的预测。
一个段长度为4的vanilla模型的示意图。
Transformer-XL是Google在2019年提出了一种语言模型训练方法(https://arxiv.org/abs/1901.02860),有两个创新点:循环机制(Recurrence Mechanism)和相对位置编码(Relative Positional Encoding),以克服vanilla Transformer捕捉长距离依赖的缺点并解决上下文碎片化问题。
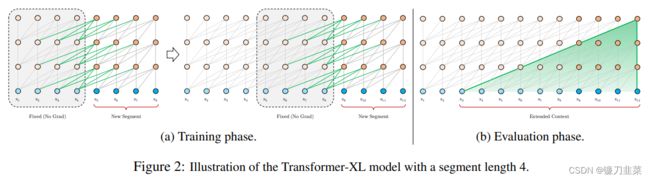
一个段长度为4的Transformer-XL模型示意图
引入循环机制
与vanilla Transformer的基本思路一样,Transformer-XL仍然是使用分段的方式进行建模,但其与vanilla Transformer的本质不同是在于引入了段与段之间的循环机制,使得当前段在建模的时候能够利用之前段的信息来实现长期依赖性。在训练时前一个段的输出只参与正向计算,而不用进行反向传播。
在训练阶段,处理后面的段时,每个隐藏层都会接收两个输入:
- 该段的前面隐藏层的输出,与vanilla Transformer相同(上图的灰色线)。
- 前面段的隐藏层的输出(上图的绿色线),可以使模型创建长期依赖关系。
这两个输入会被拼接,然后用于计算当前段的Key和Value矩阵。对于某个段的某一层的具体计算公式如下:
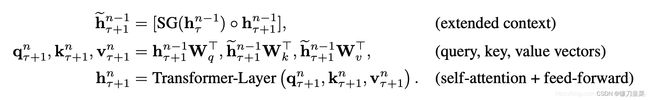
其中, τ \tau τ表示第几段, n n n表示第几层, h h h表示隐层的输出。 S G ( ⋅ ) SG(·) SG(⋅)表示停止计算梯度, [ h u ∘ h v ] [h_u \circ h_v] [hu∘hv]表示在长度维度上的两个隐层的拼接, W . W_. W.是模型参数。乍一看与Transformer中的计算公式很像,唯一关键的不同就在于Key和Value矩阵的计算上,即 k τ + 1 n k_{\tau+1}^n kτ+1n和 v τ + 1 n v_{\tau + 1}^n vτ+1n,它们基于的是扩展后的上下文隐层状态 h ~ τ + 1 n − 1 \tilde{h}_{\tau+1}^{n-1} h~τ+1n−1 进行计算, h τ n − 1 {h}_{\tau}^{n-1} hτn−1是之前段的缓存。
原则上只要GPU内存允许,该方法可以利用前面更多段的信息,测试阶段也可以获得更长的依赖。在测试阶段,与vanilla Transformer相比,其速度也会更快。在vanilla Transformer中,一次只能前进一个step,并且需要重新构建段,并全部从头开始计算;而在Transformer-XL中,每次可以前进一整个段,并利用之前段的数据来预测当前段的输出。如上图b中所示,Transformer-XL可以支持的最长依赖近似于 O ( N × L ) O(N\times L) O(N×L), L L L表示一个段的长度, N N N表示Transformer的层数。
使用相对位置编码
在Transformer中,一个重要的地方在于其考虑了序列的位置信息。在分段的情况下,如果仅仅对于每个段仍直接使用Transformer中的位置编码,即每个不同段在同一个位置上的表示使用相同的位置编码,就会出现问题。比如,第 i − 2 i-2 i−2段和第 i − 1 i-1 i−1段的第一个位置将具有相同的位置编码,但它们对于第 i i i段的建模重要性显然并不相同(例如第 i − 2 i-2 i−2段中的第一个位置重要性可能要低一些)。因此,需要对这种位置进行区分。
在Transformer模型中,将词向量和位置向量相加得到每个词最终的输入,然后进行一系列复杂的操作,涉及位置操作主要是自注意力的运算,其他的运算和位置编码没有关系。而自注意力中也只需要关注注意力分数的计算即可。
论文对于这个问题,提出了一种新的位置编码的方式,即会根据词之间的相对距离而非像Transformer中的绝对位置进行编码。在Transformer中,第一层的计算查询 q i T q_i^T qiT和键 k j k_j kj之间的attention分数的方式为:

其中, E x i E_{x_i} Exi是词 i i i的embedding, E x j E_{x_j} Exj是词 j j j的embedding, U i U_i Ui和 U j U_j Uj是位置向量,这个式子实际上是 ( W q ( E x i + U i ) ) T ⋅ ( W k ( E x j + U j ) ) (W_q(E_{x_i}+U_i))^T·(W_k(E_{x_j}+U_j)) (Wq(Exi+Ui))T⋅(Wk(Exj+Uj))的展开,就是Transformer中的标准格式。
在Transformer-XL中,对上述的attention计算方式进行了变换,转为相对位置的计算,而且不仅仅在第一层这么计算,在每一层都是这样计算。

对比来看,主要有三点变化:
- 在(b)和(d)这两项中,将所有绝对位置向量 U j U_j Uj都转为相对位置向量 R i − j R_{i-j} Ri−j,与Transformer一样,这是一个固定的编码向量,不需要学习。
- 在©这一项中,将查询的 U i T W q T U_i^TW_q^T UiTWqT向量转为一个需要学习的参数向量 u u u,因为在考虑相对位置的时候,不需要查询的绝对位置 i i i,因此对于任意的 i i i,都可以采用同样的向量。同理,在(d)这一项中,也将查询的 U i T W q T U_i^TW_q^T UiTWqT向量转为另一个需要学习的参数向量 v v v。
- 将键的权重变换矩阵 W k W_k Wk转为 W k , E W_{k, E} Wk,E和 W k , R W_{k, R} Wk,R,分别作为
content-based key vectors和location-based key vectors。
从另一个角度来解读这个公式的话,可以将attention的计算分为如下四个部分:
a. 基于内容的“寻址”,即没有添加原始位置编码的原始分数。
b. 基于内容的位置偏置,即相对于当前内容的位置偏差。
c. 全局的内容偏置,用于衡量key的重要性。
d. 全局的位置偏置,根据query和key之间的距离调整重要性。
Transformer-XL计算过程
Transformer-XL相当于Transformer中的Decoder中删除Encoder-Decoder-attention部分。结合上面两个创新点,将Transformer-XL模型的整体计算公式整理如下,这里考虑一个N层的只有一个注意力头的模型:

其中, τ \tau τ代表第几段, n n n代表第几层, h τ 0 : = E s τ h_\tau^0 := E_{s_\tau} hτ0:=Esτ定义为第 τ \tau τ段的词向量序列。值得一提的是,计算 A A A矩阵的时候,需要对所有的 i − j i-j i−j算 W k , R n R i − j W_{k,R}^nR_{i-j} Wk,RnRi−j,如果直接按照公式计算的话,计算时间是 O ( l e n g t h ) 2 O(length)^2 O(length)2,而实际上 i − j i-j i−j的范围只从0 ~ length,因此可以先计算好这length个向量,然后在实际计算 A A A矩阵时直接取用即可。
具体的,设 M M M和 L L L分别为memory和当前段序列的长度,则 i − j i-j i−j的范围也就为 0 M + L − 1 0 ~ M + L − 1 0 M+L−1。下面的 Q Q Q矩阵中的每一行都代表着 W k , R R i − j W_{k,R}R_{i-j} Wk,RRi−j中一个 i − j i-j i−j的可能性,即 Q k = W k , R R M + L − 1 − k Q_k = W_{k, R} R_{M+L-1-k} Qk=Wk,RRM+L−1−k。

则对于上面公式中的(b)项,即 q i T W k , R R i − j q_i^TW_{k,R}R_{i-j} qiTWk,RRi−j,其构成的所有可能向量的矩阵为 B B B矩阵,其形状为 L ∗ ( M + L ) L * (M + L) L∗(M+L),这是我们最终需要的(b)项的attention结果。

我们进一步定义 B ~ \tilde{B} B~矩阵为如下:

可见,需要的 B B B 矩阵的每一行只是 B ~ \tilde{B} B~的向左shift而已。因此,可以直接利用矩阵乘法计算 B ~ \tilde{B} B~即可。设 R i − j R_{i-j} Ri−j的维度为 d R d_R dR, q i q_i qi的维度为 d q d_q dq, W k , R W_{k,R} Wk,R矩阵的维度为 d q ∗ d R d_q * d_R dq∗dR,则直接计算矩阵B的时间复杂度为 2 × d q × d R × L × ( M + L ) 2\times d_q \times d_R \times L \times (M+L) 2×dq×dR×L×(M+L),而计算 B ~ \tilde{B} B~的时间复杂度为 L ∗ d q ∗ ( M + L ) + d q ∗ d R ∗ ( M + L ) L * d_q * (M + L) + d_q * d_R * (M + L) L∗dq∗(M+L)+dq∗dR∗(M+L),计算量明显不是一个量级(后者要快很多)。
同理,对于(d)项来说,可以对所有的 i − j i-j i−j定义需要的矩阵 D D D为 L × ( M + L ) L\times (M+L) L×(M+L):

可以用如下的 B ~ \tilde{B} B~来进行shift得到:
![]()
其中Q矩阵已经计算过了,也可以在这一步减少计算量。
使用PyTorch构建Transformer-XL
先从构架一个简单的Head Attention开始,然后构建多头Attention,最后构建Decoder。注意,这里Transformer-XL没有使用Encoder。
1)导入需要的库
import sys
import math
import functools
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
from typing import *
%matplotlib inline
2)定义RelativePositionalEmbedding部分
class PositionalEmbedding(nn.Module):
def __init__(self, demb):
super(PositionalEmbedding, self).__init__()
self.demb = demb
inv_freq = 1 / (10000 ** (torch.arange(0.0, demb, 2.0) / demb))
self.register_buffer('inv_freq', inv_freq)
def forward(self, pos_seq, bsz=None):
sinusoid_inp = torch.ger(pos_seq, self.inv_freq)
pos_emb = torch.cat([sinusoid_inp.sin(), sinusoid_inp.cos()], dim=-1)
if bsz is not None:
return pos_emb[:,None,:].expand(-1, bsz, -1)
else:
return pos_emb[:,None,:]
这里的demb是相对位置编码的维度,pos_seq是序列的位置向量,在代码里面是torch.arange(klen-1, -1, -1.0),其中的klen是mlen+qlen,从名称和之前的原理介绍可知这里的mlen是memory的长度,qlen是query的长度,这两者组成了key的长度。最终返回的即是 R R R向量矩阵,可见是不需要学习的。
3)定义MultiHeadAttention的部分
为了叙述方便,这里的MultiHeadAttn是源代码中的RelMultiHeadAttn和RelPartialLearnableMultiHeadAttn的整合,也即一层self-attention的计算方式。
class MultiHeadAttn(nn.Module):
def __init__(self, n_head, d_model, d_head, dropout, dropatt=0, pre_lnorm=False):
super(MultiHeadAttn, self).__init__()
self.n_head = n_head
self.d_model = d_model
self.d_head = d_head
self.dropout = dropout
self.q_net = nn.Linear(d_model, n_head * d_head, bias=False)
self.kv_net = nn.Linear(d_model, 2 * n_head * d_head, bias=False)
self.drop = nn.Dropout(dropout)
self.dropatt = nn.Dropout(dropatt)
self.o_net = nn.Linear(n_head * d_head, d_model, bias=False)
self.layer_norm = nn.LayerNorm(d_model)
self.scale = 1 / (d_head ** 0.5)
self.pre_lnorm = pre_lnorm
def forward(self, h, attn_mask=None, mems=None):
##### multihead attention
# [hlen x bsz x n_head x d_head]
if mems is not None:
c = torch.cat([mems, h], 0)
else:
c = h
if self.pre_lnorm:
##### layer normalization
c = self.layer_norm(c)
head_q = self.q_net(h)
head_k, head_v = torch.chunk(self.kv_net(c), 2, -1)
head_q = head_q.view(h.size(0), h.size(1), self.n_head, self.d_head)
head_k = head_k.view(c.size(0), c.size(1), self.n_head, self.d_head)
head_v = head_v.view(c.size(0), c.size(1), self.n_head, self.d_head)
# [qlen x klen x bsz x n_head]
attn_score = torch.einsum('ibnd,jbnd->ijbn', (head_q, head_k))
attn_score.mul_(self.scale)
if attn_mask is not None and attn_mask.any().item():
if attn_mask.dim() == 2:
attn_score.masked_fill_(attn_mask[None,:,:,None], -float('inf'))
elif attn_mask.dim() == 3:
attn_score.masked_fill_(attn_mask[:,:,:,None], -float('inf'))
# [qlen x klen x bsz x n_head]
attn_prob = F.softmax(attn_score, dim=1)
attn_prob = self.dropatt(attn_prob)
# [qlen x klen x bsz x n_head] + [klen x bsz x n_head x d_head] -> [qlen x bsz x n_head x d_head]
attn_vec = torch.einsum('ijbn,jbnd->ibnd', (attn_prob, head_v))
attn_vec = attn_vec.contiguous().view(
attn_vec.size(0), attn_vec.size(1), self.n_head * self.d_head)
##### linear projection
attn_out = self.o_net(attn_vec)
attn_out = self.drop(attn_out)
if self.pre_lnorm:
##### residual connection
output = h + attn_out
else:
##### residual connection + layer normalization
output = self.layer_norm(h + attn_out)
return output
其中n_head,d_model,d_head分别表示注意力头的个数,模型的隐层维度,每个头的隐层维度。qkv_net是用于计算query、key和value变换的参数矩阵 W q , W k , E , W v W_{q}, W_{k,E}, W_{v} Wq,Wk,E,Wv,与标准的Transformer中一致,o_net是用于将所有注意力头的结果拼接后再变换到模型维度的参数矩阵,layer_norm是LayerNormalization层,r_net是用于计算relative position embedding变换的参数矩阵 W k , R W_{k,R} Wk,R。
在前向计算的过程中,w和r分别是上一层的输出以及RelativePositionEmbedding,r_w_bias和r_r_bias分别是 u u u向量和 v v v向量,AC是前面公式中的(a)项和(c)项,BD是前面公式中的(b)项和(d)项,根据前面讲的快速计算带有相对位置的项,这里的BD需要进行偏移,即_rel_shift,经过演算,发现这里经过此函数后的BD并不是想要的B矩阵,其在B矩阵的(M+1)对角线(设主对角线为0,正数即为向右上偏移的量)的右上还有元素,不过后面紧接着就进行了mask。这里的attn_mask即为torch.triu(word_emb.new_ones(qlen, klen), diagonal=1+mlen).byte()[:,:,None]。再往后就是标准的Transformer中的add&norm环节了。
4)memory的更新过程
class MemTransformerLM(nn.Module):
def __init__(self, n_token, n_layer, n_head, d_model, d_head, d_inner,
dropout, dropatt, tie_weight=True, d_embed=None,
div_val=1, tie_projs=[False], pre_lnorm=False,
tgt_len=None, ext_len=None, mem_len=None,
cutoffs=[], adapt_inp=False,
same_length=False, attn_type=0, clamp_len=-1,
sample_softmax=-1):
super(MemTransformerLM, self).__init__()
self.n_token = n_token
d_embed = d_model if d_embed is None else d_embed
self.d_embed = d_embed
self.d_model = d_model
self.n_head = n_head
self.d_head = d_head
self.word_emb = AdaptiveEmbedding(n_token, d_embed, d_model, cutoffs,
div_val=div_val)
self.drop = nn.Dropout(dropout)
self.n_layer = n_layer
self.tgt_len = tgt_len
self.mem_len = mem_len
self.ext_len = ext_len
self.max_klen = tgt_len + ext_len + mem_len
self.attn_type = attn_type
self.layers = nn.ModuleList()
if attn_type == 0: # the default attention
for i in range(n_layer):
self.layers.append(
RelPartialLearnableDecoderLayer(
n_head, d_model, d_head, d_inner, dropout,
tgt_len=tgt_len, ext_len=ext_len, mem_len=mem_len,
dropatt=dropatt, pre_lnorm=pre_lnorm)
)
elif attn_type == 1: # learnable embeddings
for i in range(n_layer):
self.layers.append(
RelLearnableDecoderLayer(
n_head, d_model, d_head, d_inner, dropout,
tgt_len=tgt_len, ext_len=ext_len, mem_len=mem_len,
dropatt=dropatt, pre_lnorm=pre_lnorm)
)
elif attn_type in [2, 3]: # absolute embeddings
for i in range(n_layer):
self.layers.append(
DecoderLayer(
n_head, d_model, d_head, d_inner, dropout,
dropatt=dropatt, pre_lnorm=pre_lnorm)
)
self.sample_softmax = sample_softmax
# use sampled softmax
if sample_softmax > 0:
self.out_layer = nn.Linear(d_model, n_token)
if tie_weight:
self.out_layer.weight = self.word_emb.weight
self.tie_weight = tie_weight
self.sampler = LogUniformSampler(n_token, sample_softmax)
# use adaptive softmax (including standard softmax)
else:
self.crit = ProjectedAdaptiveLogSoftmax(n_token, d_embed, d_model,
cutoffs, div_val=div_val)
if tie_weight:
for i in range(len(self.crit.out_layers)):
self.crit.out_layers[i].weight = self.word_emb.emb_layers[i].weight
if tie_projs:
for i, tie_proj in enumerate(tie_projs):
if tie_proj and div_val == 1 and d_model != d_embed:
self.crit.out_projs[i] = self.word_emb.emb_projs[0]
elif tie_proj and div_val != 1:
self.crit.out_projs[i] = self.word_emb.emb_projs[i]
self.same_length = same_length
self.clamp_len = clamp_len
self._create_params()
def backward_compatible(self):
self.sample_softmax = -1
def _create_params(self):
if self.attn_type == 0: # default attention
self.pos_emb = PositionalEmbedding(self.d_model)
self.r_w_bias = nn.Parameter(torch.Tensor(self.n_head, self.d_head))
self.r_r_bias = nn.Parameter(torch.Tensor(self.n_head, self.d_head))
elif self.attn_type == 1: # learnable
self.r_emb = nn.Parameter(torch.Tensor(
self.n_layer, self.max_klen, self.n_head, self.d_head))
self.r_w_bias = nn.Parameter(torch.Tensor(
self.n_layer, self.n_head, self.d_head))
self.r_bias = nn.Parameter(torch.Tensor(
self.n_layer, self.max_klen, self.n_head))
elif self.attn_type == 2: # absolute standard
self.pos_emb = PositionalEmbedding(self.d_model)
elif self.attn_type == 3: # absolute deeper SA
self.r_emb = nn.Parameter(torch.Tensor(
self.n_layer, self.max_klen, self.n_head, self.d_head))
def reset_length(self, tgt_len, ext_len, mem_len):
self.tgt_len = tgt_len
self.mem_len = mem_len
self.ext_len = ext_len
def init_mems(self):
if self.mem_len > 0:
mems = []
param = next(self.parameters())
for i in range(self.n_layer+1):
empty = torch.empty(0, dtype=param.dtype, device=param.device)
mems.append(empty)
return mems
else:
return None
def _update_mems(self, hids, mems, qlen, mlen):
# does not deal with None
if mems is None: return None
# mems is not None
assert len(hids) == len(mems), 'len(hids) != len(mems)'
# There are `mlen + qlen` steps that can be cached into mems
# For the next step, the last `ext_len` of the `qlen` tokens
# will be used as the extended context. Hence, we only cache
# the tokens from `mlen + qlen - self.ext_len - self.mem_len`
# to `mlen + qlen - self.ext_len`.
with torch.no_grad():
new_mems = []
end_idx = mlen + max(0, qlen - 0 - self.ext_len)
beg_idx = max(0, end_idx - self.mem_len)
for i in range(len(hids)):
cat = torch.cat([mems[i], hids[i]], dim=0)
new_mems.append(cat[beg_idx:end_idx].detach())
return new_mems
def _forward(self, dec_inp, mems=None):
qlen, bsz = dec_inp.size()
word_emb = self.word_emb(dec_inp)
mlen = mems[0].size(0) if mems is not None else 0
klen = mlen + qlen
if self.same_length:
all_ones = word_emb.new_ones(qlen, klen)
mask_len = klen - self.mem_len
if mask_len > 0:
mask_shift_len = qlen - mask_len
else:
mask_shift_len = qlen
dec_attn_mask = (torch.triu(all_ones, 1+mlen)
+ torch.tril(all_ones, -mask_shift_len)).byte()[:, :, None] # -1
else:
dec_attn_mask = torch.triu(
word_emb.new_ones(qlen, klen), diagonal=1+mlen).byte()[:,:,None]
hids = []
if self.attn_type == 0: # default
pos_seq = torch.arange(klen-1, -1, -1.0, device=word_emb.device,
dtype=word_emb.dtype)
if self.clamp_len > 0:
pos_seq.clamp_(max=self.clamp_len)
pos_emb = self.pos_emb(pos_seq)
core_out = self.drop(word_emb)
pos_emb = self.drop(pos_emb)
hids.append(core_out)
for i, layer in enumerate(self.layers):
mems_i = None if mems is None else mems[i]
core_out = layer(core_out, pos_emb, self.r_w_bias,
self.r_r_bias, dec_attn_mask=dec_attn_mask, mems=mems_i)
hids.append(core_out)
elif self.attn_type == 1: # learnable
core_out = self.drop(word_emb)
hids.append(core_out)
for i, layer in enumerate(self.layers):
if self.clamp_len > 0:
r_emb = self.r_emb[i][-self.clamp_len :]
r_bias = self.r_bias[i][-self.clamp_len :]
else:
r_emb, r_bias = self.r_emb[i], self.r_bias[i]
mems_i = None if mems is None else mems[i]
core_out = layer(core_out, r_emb, self.r_w_bias[i],
r_bias, dec_attn_mask=dec_attn_mask, mems=mems_i)
hids.append(core_out)
elif self.attn_type == 2: # absolute
pos_seq = torch.arange(klen - 1, -1, -1.0, device=word_emb.device,
dtype=word_emb.dtype)
if self.clamp_len > 0:
pos_seq.clamp_(max=self.clamp_len)
pos_emb = self.pos_emb(pos_seq)
core_out = self.drop(word_emb + pos_emb[-qlen:])
hids.append(core_out)
for i, layer in enumerate(self.layers):
mems_i = None if mems is None else mems[i]
if mems_i is not None and i == 0:
mems_i += pos_emb[:mlen]
core_out = layer(core_out, dec_attn_mask=dec_attn_mask,
mems=mems_i)
hids.append(core_out)
elif self.attn_type == 3:
core_out = self.drop(word_emb)
hids.append(core_out)
for i, layer in enumerate(self.layers):
mems_i = None if mems is None else mems[i]
if mems_i is not None and mlen > 0:
cur_emb = self.r_emb[i][:-qlen]
cur_size = cur_emb.size(0)
if cur_size < mlen:
cur_emb_pad = cur_emb[0:1].expand(mlen-cur_size, -1, -1)
cur_emb = torch.cat([cur_emb_pad, cur_emb], 0)
else:
cur_emb = cur_emb[-mlen:]
mems_i += cur_emb.view(mlen, 1, -1)
core_out += self.r_emb[i][-qlen:].view(qlen, 1, -1)
core_out = layer(core_out, dec_attn_mask=dec_attn_mask,
mems=mems_i)
hids.append(core_out)
core_out = self.drop(core_out)
new_mems = self._update_mems(hids, mems, mlen, qlen)
return core_out, new_mems
def forward(self, data, target, *mems):
# nn.DataParallel does not allow size(0) tensors to be broadcasted.
# So, have to initialize size(0) mems inside the model forward.
# Moreover, have to return new_mems to allow nn.DataParallel to piece
# them together.
if not mems: mems = self.init_mems()
tgt_len = target.size(0)
hidden, new_mems = self._forward(data, mems=mems)
pred_hid = hidden[-tgt_len:]
if self.sample_softmax > 0 and self.training:
assert self.tie_weight
logit = sample_logits(self.word_emb,
self.out_layer.bias, target, pred_hid, self.sampler)
loss = -F.log_softmax(logit, -1)[:, :, 0]
else:
loss = self.crit(pred_hid.view(-1, pred_hid.size(-1)), target.view(-1))
loss = loss.view(tgt_len, -1)
if new_mems is None:
return [loss]
else:
return [loss] + new_mems
这里_update_mems函数的hids是当前段每层的输出,mems为当前段每层依赖的memory,qlen为序列长度,mlen为当前段依赖的memory的长度。
5)构建Decoder
在Decoder模块中,除了MultiHeadAttention层外,还有前馈网络层
class PositionwiseFF(nn.Module):
def __init__(self, d_model, d_inner, dropout, pre_lnorm=False):
super(PositionwiseFF, self).__init__()
self.d_model = d_model
self.d_inner = d_inner
self.dropout = dropout
self.CoreNet = nn.Sequential(
nn.Linear(d_model, d_inner), nn.ReLU(inplace=True),
nn.Dropout(dropout),
nn.Linear(d_inner, d_model),
nn.Dropout(dropout),
)
self.layer_norm = nn.LayerNorm(d_model)
self.pre_lnorm = pre_lnorm
def forward(self, inp):
if self.pre_lnorm:
##### layer normalization + positionwise feed-forward
core_out = self.CoreNet(self.layer_norm(inp))
##### residual connection
output = core_out + inp
else:
##### positionwise feed-forward
core_out = self.CoreNet(inp)
##### residual connection + layer normalization
output = self.layer_norm(inp + core_out)
return output
Decoder模块的代码如下:
class DecoderLayer(nn.Module):
def __init__(self, n_head, d_model, d_head, d_inner, dropout, **kwargs):
super(DecoderLayer, self).__init__()
self.dec_attn = MultiHeadAttn(n_head, d_model, d_head, dropout, **kwargs)
self.pos_ff = PositionwiseFF(d_model, d_inner, dropout, pre_lnorm=kwargs.get('pre_lnorm'))
def forward(self, dec_inp, dec_attn_mask=None, mems=None):
output = self.dec_attn(dec_inp, attn_mask=dec_attn_mask,mems=mems)
output = self.pos_ff(output)
return output
这里只列出部分代码,完整代码请看Transformer-XL官方代码:https://github.com/kimiyoung/transformer-xl/tree/master
Reformer
谷歌推出了Reformer架构,Transformer模型旨在有效地处理处理很长的时间序列的数据(例如,在语言处理多达100万个单词)。Reformer的执行只需要更少的内存消耗,并且即使在单个GPU上运行也可以获得非常好的性能。论文Reformer: The efficient Transformer在ICLR 2020上发表(并在评审中获得了近乎完美的分数)。Reformer模型有望通过超越语言应用(如音乐、语音、图像和视频生成)对该领域产生重大影响。
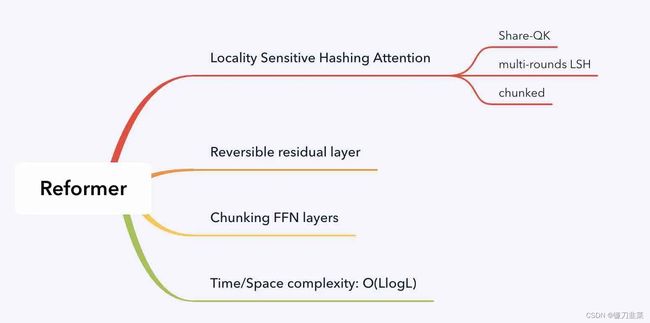
Reformer就是为了解决Transformer计算复杂度过大以及占用内存过多的问题而提出的。它的核心目的主要体现在两个方面:
1)将传统的多头注意力机制改为使用局部敏感哈希(Locality-Sensitive Hashing, LSH)的注意力机制;
2)使用逆Transformer(Reversible Transformer)
使用局部敏感哈希
在深度学习中,注意力是一种机制,它使网络能够根据上下文的不同部分与当前时间步长之间的相关性,将注意力集中在上下文的不同部分。transformer模型中存在三种注意机制:

在Transformer 模型三种类型的注意力
在Transformer 中使用的标准注意里是缩放的点积,表示为:

从上面的方程和下面的图,它可以观察到,QKᵀ的计算和内存的消耗都是 O (L²) 复杂度的,这是主要的内存瓶颈。
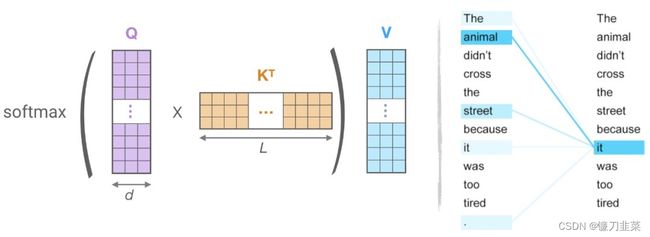
图4:(左):点积注意力的主要计算,(右)token(“it”)对于序列(“the”、“animal”、“street”、“it”、“it”)的注意力子集。
但这是计算和存储完整的矩阵QKᵀ是必要的吗 ?答案是不, 我们感兴趣的是softmax*(QKᵀ ),它是由最大的元素决定的,通常是稀疏矩阵。因此,正如上面的示例中所看到的,对于每个查询q,我们只需要注意最接近q的键k。例如,如果长度是64K,对于每个q,我们可以只考虑32或64个最近的键的一个小子集。因此,注意力机制查找query的最近邻居键,但效率不高。这是不是让你想起了最近邻搜索?
LSH的核心思想就是:向量空间里相近的两个向量,经过hash函数后依然是相近的。在这里计算Q和K的点积就是为了找到Q和K相似的部分,所以没有必要把Q中的每个向量都与K相乘,可以只计算相近的部分。经过LSH,可将计算复杂度降低到 O ( L l o n g L ) O(L long L) O(LlongL)。LSH的原理如图所示:

对于每一句话,首先使用LSH来对每个快进行分桶,将相似的部分放在同一个桶里面。然后将每一个桶并行化后分别计算其中的点积。此外,该方法还考虑到了有一定概率相似的向量会被分割到不同的桶里的情况。
使用可逆残差网络
LSH解决了计算复杂度的问题,这一部分则是为了解决内存占用的问题。Transformer中存在很多残差连接部分,每一个残差连接都需要我们存储它的输入,供后面的反向传播使用,这就导致了严重的内存浪费。
Reformer借鉴了可逆残差网络(RevNet)的思想,不在保存中间层残差连接部分的输入,只需要知道最后一层的输入就可以得出中间层的输入,用可逆网络降低残差内存开销。使用可逆残差网络解决内存占用问题的基本原理如下:
1)普通的残差网络形式为 y = x + f ( x ) y=x+f(x) y=x+f(x),无法从y中倒推出x。
2)把输入 x x x变成 x 1 x_1 x1和 x 2 x_2 x2,然后用两个函数F和G来进行残差连接,分别得到 y 1 y_1 y1和 y 2 y_2 y2,可逆残差网络的形式为: y 1 = x 1 + F ( x 2 ) , y 2 = x 2 + G ( x 1 ) y_1=x_1+F(x_2), y_2=x_2+G(x_1) y1=x1+F(x2),y2=x2+G(x1)
3)通过减法倒推可得: x 1 = y 1 − F ( x 2 ) , x 2 = y 2 − G ( x 1 ) x_1=y_1-F(x_2),x_2=y_2-G(x_1) x1=y1−F(x2),x2=y2−G(x1)
这里函数F就是注意力计算,而函数G就是前馈网络。
分块
在Reformer的效率改进的最后一部分处理第三个问题,即前馈层的高维中间向量 — 可以达到4K和更高的维度。由于前馈层的计算是独立于序列的各个位置的,所以前向和后向的计算以及反向的计算都可以被分割成块。例如,对于向前传递,我们将有:
![]()
前向通道计算中的分块
总结
Transformer采用了Encoder-Decoder模型,但在编码器或解码器中使用了多头注意力机制,使性能有了一个飞跃。对于Transformer的改进,有:Transformer-XL和Reformer。这两个改进版本的基本出发点都是降低资源使用量,增加输入片段的长度等。
参考资料
- Transformer 模型的 PyTorch 实现
- Building the Mighty Transformer for Sequence Tagging in PyTorch : Part II
- Attention Is All You Need
- The Annotated Transformer的中文注释版
- transformer的细节到底是怎么样的?
- Transformer-XL解读
- Reformer 详解


