从钻尖轮廓到螺旋槽截线轮廓

图1：钻尖图像

图2：提取的轮廓

图3：螺旋槽截面轮廓

 本案例实现从图1磨尖后的螺旋槽截线到图2磨尖前螺旋槽截线的求解。具体如下：

import sympy as sy
import numpy as np
import matplotlib.pyplot as plt
import time
start=time.perf_counter()
'''
坐标系定义
​
坐标系原点为：中线与横刃的交点
y轴：中线
x轴：中线的垂线
​
参数字典
theta_value1：第一后刀面与与XOY面夹角（180°-第一后角）
theta_value2：第二后刀面与与XOY面夹角（180°-第二后角）
R：料棒半径
delta0：螺旋角
rotate_blank：横刃和中线的夹角，暂时手动测量
'''
pr={"theta_value1":(180-12)*np.pi/180,"theta_value2":(180-30)*np.pi/180,"R":0.306/2,"delta0":40*np.pi/180,"rotate_blank":-46*np.pi/180}
#定义读取txt文件的函数，每行存储一个点的x，y，z坐标，用逗号间隔，这里为刃面投影数据，Z无意义
def openreadtxt(file_name):
    data = []
    with open(file_name, 'r') as file:
        file_data = file.readlines()  # 读取所有行
        for row in file_data:
            tmp_list = row.split(',')
            tmp = [float(x) for x in tmp_list]
            data.append(tmp)  # 将每行数据插入data中
    return data
#轮廓点存储路径
filename1 ="USF0.30-6.2_t1.txt"
#读取轮廓点，转化为数组
data = openreadtxt(filename1)
X = np.array(data)[:, 0]
Y = np.array(data)[:, 1]
#截取主切削刃数据，由起始位置控制，起始位置手动确认
l1x=X[80:120]
l1y=Y[80:120]
#将读取的轮廓点顺时针旋转横刃与中线的夹角后，截取拐弯的数据，截取位置手动确认
X_r = X*np.cos(pr["rotate_blank"])+Y*np.sin(pr["rotate_blank"])
Y_r = -X*np.sin(pr["rotate_blank"])+Y*np.cos(pr["rotate_blank"])
l2x=X_r[120:280]
l2y=Y_r[120:280]
​
#定义右旋螺旋运动的矩阵变换
# 定义符号和角度
x,y,z, R, delta0, vw = sy.symbols('x y z R delta0 vw')
rw = sy.Matrix([x, y, z])
k = R / sy.tan(delta0)
WtoF = sy.Matrix([[sy.cos(vw), -sy.sin(vw), 0], [sy.sin(vw), sy.cos(vw), 0], [0, 0, 1]])
Trans1 = sy.Matrix([0, 0, k * vw])
Rf_expr = WtoF.inv() * (rw -Trans1)
​
​
​
#定义平面方程
#此平面垂直于YOZ面
# 计算交点z坐标
theta = sy.symbols('theta')
f_plame=y*sy.tan(theta)
f_plame_fn1=sy.lambdify((y),f_plame.subs({theta:pr["theta_value1"]}))
f_plame_fn2=sy.lambdify((y),f_plame.subs({theta:pr["theta_value2"]}))
#由主切削刃和拐弯数据点的投影求其Z坐标
Z1=f_plame_fn1(l1y)
Z2=f_plame_fn2(l2y)
​
#求取螺旋槽截线
#将右旋螺旋运动的Z坐标公式转化为numpy
f_Rf=Rf_expr[2]
f_Rf_fn=sy.lambdify((R, delta0, vw,z), f_Rf)
Rf_fn = sy.lambdify((R, delta0, vw,x,y,z), Rf_expr)
vw_range = np.linspace(0, 2 * np.pi, 1000)  # vw的范围，将其分成1000个等间隔点
#求主切削刃数据对应的螺旋槽截线
vw_coll1=[]
Rf_intersect1 = []
for zi in Z1:
    ffn = f_Rf_fn(pr["R"], pr["delta0"], vw_range,zi)
    pos=np.argmin(np.abs(ffn))
    vw_coll1.append(vw_range[pos])
for xi,yi,zi,vi in zip(l1x, l1y,Z1,vw_coll1):
    Rf = Rf_fn(pr["R"], pr["delta0"],vi,xi, yi, zi)
    Rf_intersect1.append(Rf)
Rf_intersect1 = np.array(Rf_intersect1).squeeze()
#求旋转后的拐弯数据对应的螺旋槽截线
vw_coll2=[]
Rf_intersect2 = []
for zi in Z2:
    ffn = f_Rf_fn(pr["R"], pr["delta0"], vw_range,zi)
    pos=np.argmin(np.abs(ffn))
    vw_coll2.append(vw_range[pos])
for xi,yi,zi,vi in zip(l2x, l2y,Z2,vw_coll2):
    Rf = Rf_fn(pr["R"], pr["delta0"],vi,xi, yi, zi)
    Rf_intersect2.append(Rf)
Rf_intersect2 = np.array(Rf_intersect2).squeeze()
#按拐弯的旋转角度，反向旋转回去
Rf_intersect2_xr = Rf_intersect2[:,0]*np.cos(-pr["rotate_blank"])+Rf_intersect2[:,1]*np.sin(-pr["rotate_blank"])
Rf_intersect2_yr = -Rf_intersect2[:,0]*np.sin(-pr["rotate_blank"])+Rf_intersect2[:,1]*np.cos(-pr["rotate_blank"])
#计算程序用时
end = time.perf_counter()
execution_time = end - start
print(f"代码执行时间：{execution_time}秒")
#作图
fig = plt.figure(figsize=(5, 5))
plt.rcParams['xtick.direction'] = 'in'  # 将x周的刻度线方向设置向内
plt.rcParams['ytick.direction'] = 'in'  # 将y轴的刻度方向设置向内
clist = ['blue', 'red', 'green', 'black', 'darkgreen', 'lime', 'gold', 'purple', 'green', 'cyan', 'salmon', 'grey',
             'mediumvioletred', 'darkkhaki', 'gray', 'darkcyan', 'violet', 'powderblue']
# ==========================================
# 参数方程画料棒圆形
theta_blank = np.arange(0, 2 * np.pi, 0.01)
x_blank = 0 + pr["R"] * np.cos(theta_blank)
y_blank = 0 + pr["R"] * np.sin(theta_blank)
plt.plot(x_blank, y_blank, c=clist[0])
#画主切削刃对应的截线
plt.scatter(Rf_intersect1[:,1],Rf_intersect1[:,0],label="from primary face")
# plt.scatter(Rf_intersect2[:,1],Rf_intersect2[:,0],label="from primary face")
#画拐弯对应的截线
plt.scatter(Rf_intersect2_yr,Rf_intersect2_xr,label="from secondary face")
#画主切削刃
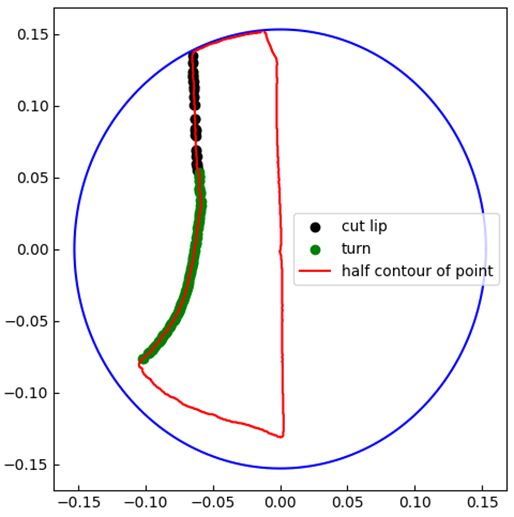
plt.plot(Y[80:120],X[80:120],c='r',label="cut lip")
#画拐弯
plt.plot(Y[120:280],X[120:280],c='k',label="turn")
plt.legend()
plt.tight_layout()
plt.show()
#合并两条截线
xx=np.concatenate((Rf_intersect1[:,0],Rf_intersect2_xr))
yy=np.concatenate((Rf_intersect1[:,1],Rf_intersect2_yr))
#保存截线数据，用于后续分析
# def save_points_to_file(Point_x,Point_y, filename):
#     with open(filename, 'w') as file:
#         for i in range(len(Point_x)):
#             x, y, z = Point_x[i],Point_y[i],0.0
#             file.write(f"{x},{y},{z}\n")
# filename2="USF0.30-6.2_tr1.txt"
# save_points_to_file(xx,yy,filename2)

图4：求解结果