编程题四大算法思想（一）——分治法：最大子数组问题、矩阵乘法的Strassen算法、凸包问题、二维最近点对问题

分治法

• 方法
  • 分治策略
  • 分治法效率分析——迭代法（递归树法）
  • 分治法效率分析——主定理方法

注：这两个效率分析的方法，详见另一篇博客“数据结构与算法（一）——绪论”。

https://blog.csdn.net/weixin_44421143/article/details/132193847

• 问题

  • 最大子数组问题

  • 矩阵乘法的Srassen算法

  • 最近点对问题

  • 凸包问题

分治策略

• 分治法思想

  将原问题分成n个规模较小而结构与原问题相似的子问题，递归地解这些子问题，然后合并其结果就得到原问题的解。

• 分而治之（divide - and - conquer）

  • 分解（Divide）

    原问题分为若干子问题，这些子问题是原问题的规模较小的实例。

  • 解决（Conquer）

    递归地求解各子问题。若子问题足够小，则直接求解。

  • 合并（Combine）

    将子问题的解合并成原问题的解。

    关键在于合并处理。

分治算法的效率分析

• 用递归式分析分治算法的运行时间。
• 一个递归式是一个函数，它由一个或多个基本情况（base case），它自身，以及小参数组成。
• 递归式的解可以用来近似算法的运行时间。

$T(n)$本身表示的就是时间代价。对于函数$T(n)$而言，它的时间代价是基于$T(n-1)$的基础之上的，但是加$1$。

为什么要加1，因为它是在$T(n-1)$所需要花费的时间代价之外还需多执行一个乘法操作。

这就形成了一个递归关系式。

递归关系式体现的是，我的大问题，和小问题，之间的关系。

那我知道$T(n)=T(n-1)+1$，但是$T(n-1)$我也不知道啊，我还是不知道啊？

你一直往下递推，一直递归到$T(1)$。最后$T(n)$具体的时间代价不就求出来了。

归并排序

  初始序列我不断地分成两个子问题。直到分解到最后，每个子序列里只剩一个了。

  然后开始合并，两两合并。

具体应用问题

（一）最大子数组问题

问题：

• 输入：数值数组A[1..n]
  • 假设数组中存在负数
  • 如果数组中全是非负数，该问题很简单。
• 输出：数组下标i和j使得子数组A[i..j]为A[1..n]的和最大的非空连续子数组。

---

啥意思呢？

• 考虑下面的情景：

  • 一只股票连续n天的交易价格。
  • 什么时候该买入？什么时候该卖出？

• 这个问题就可以转换成最大子数组问题。

定义：A[i] = (第i天的价格) - (第i-1天的价格)

即，我今天的价格，比昨天涨了多少（正数）、跌了多少（负数）。

• 如果最大子数组是A[i..j]
  • 第i天买入
  • 第j天卖出

即，我到底从哪天买入、到哪天卖出，我从而能够赚的最多。

---

例子1

• 一支股票连续n天的交易价格：

看右边的表格，它的最后一行，就对应于整个数组A[1..n]。

什么是最大子数组，就是，我到底是哪天买入（i）、哪天卖出（j），才是最赚的情况，对应于最大子数组A[i..j]。

进一步想一下，“最赚的”是啥意思。——就是最终卖出价格与最初买入价格之间的差最大。——或者说，是A[i]+...+A[j]这些数求和为最大值。

• 对于这个例子，其最大子数组为A[3..3]。即第三天当天买入，当天卖出。

例子2

• 一支股票连续n天的交易价格：

• 最大子数组是A[8..11]。

咋看出来的？？——若从图像上直观来看，可以理解为，图像的某一个极小值点与某一个极大值点之间的差为最大的情况（前提：极小值点的选取要从时间上位于极大值点前）。所以从上图，若直观的观察，也能观察出，第7天对应的一个很低价买入，第11天对应的很高价卖出，获利会是最大了。——为啥数组是A[8]，这有可能是因为，我们具体的数组存放，和我们所谓的第7天，它不是完全对照的，它可能是有个对应关系。

关键就看计算机咋实现了。

我们在解决问题的时候，一般都是从蛮力法开始。我们不会一上来就想象出来一种很精妙的办法。

蛮力法

  你不是有n个元素么，我不就是要找出最大差值么？

  那我就从第一个元素开始：A[1..1]是多少，A[1..2]是多少，A[1..3]是多少，……A[1..n]是多少。——n次

  然后从第二个元素开始：A[2..2]，A[2..3]，A[2..4],……,A[2..n]。——n-1次

  …………

  从第n-1个元素开始：A[n-1..n-1]，A[n-1..n]。——2次

  从第n个元素开始：A[n..n]。——1次

  蛮力法是啥，我就是把所有情况列出来么。

  总共有$1+2+...+n=\frac{n(n+1)}{2}$种可能性。

  但是，对于其中的操作，我们总是要做一个求和的操作。对于“从第一个元素开始”下的情况，我们对A[1..1]，一直求到A[1..n]，分别为1、2、3、…n个数求和。——我们对于n个数字，前1、2、…、n个数之和的求和，要获取这n个值，共需要进行$n^2$次的操作。而我们又不仅仅需要算“第一个元素开始”的情况，也要算其他的情况，所以总的时间代价还要再乘上$n$，为$O(n^3)$。

  这个求和操作，能否优化一下？——求前缀和。

  实际上，你求完A[1..1]得到的和（第一个数字），之后你在算A[1..2]之和时（前两个数之和）就完全不必从头加起，而是由上一个的结果基础之上加一个数即可。因此，我们对于n个数字，获取前1、2、…、n个数之和，这n个值，只需要进行$n$次的操作。因此，总共的算法为$O(n^2)$。

---

  我们既然蛮力法已经会求了——时间复杂度$O(n^2)$。

  那么我们再来看看，这个问题用分治法怎么求？

分治法

  分治法，同样也是个，n个元素的数组。

  但是，我对这个数组，我考虑的是，把它从中间分成两半。——三个位置：$low,high,mid$。

  我的一个初步的想法：左半边数组，找到它的最大子数组A[i1, j1]，右半边数组它的最大子数组A[i2,j2]。然后再看看这两个最大子数组谁更大，最终就是整个数组的最大子数组了。

  但是，稍加思考，这个思路就明显有个问题：我的最大子数组凭什么就一定是从左半边某处起、左半边某处停止；或者右半边某处起、右半边某处止？——我完全有可能是横跨mid的情况啊。

  所以对这个问题的分治法处理，还是有点麻烦的了。因为它除了对左右两边分别处理之外，还有一个对于“中间”处理的过程。

---

该问题的分治解法总结如下：

• 子问题：找出$A[low..high]$的最大子数组。
  • 参数初始值：$low=1,high=n.$
  • 分解。将子数组分解成两个大小基本相同的子数组。
    • 找到子数组的中间位置$mid$，将子数组分成两个更小的子数组$A[low..mid]$和$A[mid+\mathrm{1..}high]$。
  • 求解。找数组$A[low..high]$和$A[mid+\mathrm{1..}high]$的最大子数组。
  • 组合。找出跨越中间位置的最大子数组。
    • 三种情况取和最大的子数组（跨越中间位置的最大子数组和“求解”步骤中找到的那两个最大子数组）。

---

这时候会发现，问题在于，跨越中间位置的最大子数组咋找啊？

找跨越中间位置的最大子数组

• 子数组必须跨越中间位置。
• 解决思路：
  • 任何一个跨越中间位置$A[mid]$的子数组$A[i..j]$由两个更小的子数组$A[i..mid]$和$A[mid+\mathrm{1..}j]$组成，其中$low\le i\le mid\le j\le high$。
  • 只要找到最大子数组$A[i..mid]$和$A[mid+\mathrm{1..}j]$，然后把它们合并。
  • 注意：$mid$是固定的，左右分别扫描即可。这个问题可以用$\theta (n)$的时间解决。

（可能上面的说法还是有点抽象，下面形象一点来解释）

  实际上对于这一块，也是靠蛮力了。

  $mid$是一个已经固定好的位置。我从$mid$出发，往左边找：我往左1个、往左2个、往左3个、……一直往左到$low$的位置为止。我们找啥？——我们找，这所有情况里，哪种是最大的。往右边找是同理的。

  对于这两边的蛮力找法，总共操作也就是$O(n)$的时间。

  这样一来，我们通过对以$mid$为终点，左边起点所有情况的遍历，找出最大的那一情况：$A[i..mid]$。通过对以$mid$为起点，右边终点所有情况的遍历，找出最大的那一情况：$A[mid+\mathrm{1..}j]$。把这两个连起来，就是一个跨越$mid$的最大子数组了。

---

时间复杂度

时间复杂度为：$T(n)=2T(n/2)+O(n)$。

其中，$O(n)$是蛮力解决跨界子数组的时间。

中间的推理过程不写了，最后结果如下图所示。

（二）矩阵乘法

  具体的矩阵乘法定义就不说了，学过线性代数的都知道。

蛮力算法

Matrix operator*(const Matrix &m, const Matrix &n) {
    if(m.l_size()!=n.h_size()) return Matrix();	//非法运算返回空矩阵
    
    Matrix ans(m.h_size(), n.l_size());
    
    for(int i=0; i!=ans.h_size(); ++i) {
        for(int j=0; j!=ans.l_size(); ++j) {
            for(int k=0; k!=m.l_size(); ++k) {
                ans[i][j] += m[i][k]*n[k][j];
            }
        }
    }
    return ans;
}

  通过看这个代码，或者根据矩阵乘法的定义来想一下，很容易能想到，蛮力法是$O(n^3)$。

  那既然蛮力法不好，那怎么写比较好呢？——还是分治呗。

分治法

• 分治法：
  • 将矩阵$A$，$B$和$C$中每一矩阵都分块成$4$个大小相等的子矩阵。由此，可将方程$C=AB$重写为：

  由此可得：

注意：只关心乘法的执行次数。

  我们把一个矩阵，分解成8个子矩阵的相乘问题。（只关心乘法操作）至于其他的操作，如相加操作，它们可视为一个常量时间$O(1)$。

由此可得：$T(n)=8T(n/2)+O(1)$

---

时间复杂度

  具体的推导过程不写了，最后得到，这种方法得到的时间复杂度为$T(n)=\theta (n^3)$。

  我们会发现，它跟蛮力法时间复杂度一样了，没改进啊。

  想一下，我们都用分治法了，为啥没有改进。因为乘8。——具体原因，看一看主定理分析时间复杂度那里，有个$lo{g}_{b}a$的问题。

Strassen矩阵乘法

• 为了降低时间复杂度，必须减少乘法的次数。

  对于矩阵的加法，我们可以理解为一个$O(n)$时间的操作。

  他这个人研究的这个算法，为啥好？就是因为他只做了$7$次矩阵乘法，其余的均为$O(1)$的矩阵加法操作。

由此可得：$T(n)=7T(n/2)+O(1)$。

具体推理过程不写了，最终得到它这个算法的时间复杂度$\approx n^{2.807}$。

（三）凸包问题

直观引入一下

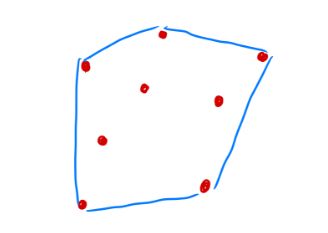
• 定义：对于平面上的一个点集合（有限或无限），如果以集合中任意两点P和Q为端点的线段都属于这个集合，则这个集合是凸的。

任意两个点连接成的线段，都位于这个包（“包围”）的里面。

左边这些都是凸包；右边那些都不是凸包。

---

知道是不是凸包，有啥用？

举个例子：比如我们疫情的时候，在地图上来看，下面红点标注的地区是高风险地区，如图。那么我们就可以对这些点的集合研究一个凸包，作为我们防护的范围。

说白了就是一个找边界的问题。

---

• 定义：一个点集合S的凸包是包含S的最小凸集合。

对于一个点集合，我可以找一个最小的，也可以往大一点去找、也可以往更大的范围去找。

但是现在要求我们找的是一个最小的，才算作它的凸包。

不是说随便画一个就行。那我尽量画一个特别大的不就完事了。

• 通俗理解：用皮筋绑着定点集边缘，皮筋内的区域就是凸包。

相当于得到一个最外边的一个区域边界。

• 特点：任意两个“极点”连成的直线，其他的点都在这条直线的一侧。（如下图红线就是两个极点的连线，其他点都在它的一侧；而蓝线不是）

---

凸包问题

• 定理：任意包含$n>2$个点（不共线）的集合$S$的凸包是以$S$中的某些点为顶点的凸多边形。
• 凸包问题是为一个$n$个点的集合构造凸包的问题。
• 极点：对于任何以集合中的点为端点的线段来说，它们不是这种线段的中间点。

这个“不是中点”是啥意思呢。首先不要忘了这是一个点集合。

对于凸包内部的一些点，把它们连接的时候，它们有可能成为连接出的这个线段的中间点。（假设上图中P8和P4和P1能连接成一条线段，那P4就是中间的一个点）

但是对于极点，你无论什么情况，无论跟谁连，咋连，都不可能是连出来的线段的中间的点，只能是端点。因为你极点的另一侧是不可能有点的。

• 极点：两个极点连成的线，其他所有点都在这条线的一侧。

这个方式理解也可以。

---

在直线一侧如何检测（方向检测）

我们咋样能知道，这个点r就是在这个直线pq的一侧呢？或者具体是在哪一侧呢？

向量叉乘。——不错，但是大概不用这么麻烦。

我们可以简单的这样来看：

  对于p、q构成的一条直线$f(x,y)=0$而言，再来看点r的坐标$(x_0,y_0)$的话。

  如果它符合$f(x_0,y_0)=0$，那就说明点r在直线上；

  如果它符合$f(x_0,y_0)>0$，那就说明点r在直线的某一侧；

  如果它符合$f(x_0,y_0)<0$，那就说明点r在直线的另一侧。

  而p、q构成的这条直线，直线方程也很好写，就是：
$$\frac{y-p_y}{x-p_x}=\frac{q_y-p_y}{q_x-p_x}$$
  但对于这个东西而言，它涉及除法，在我们计算机里面不好处理、有点复杂。

  那好办，给它换成乘法就行了，如下：
$$(y-p_y)(q_x-p_x)-(x-p_x)(q_y-p_y)=0$$
  而对于这个式子，我们可以把它转换成行列式的表示，如下：
∣ 1 p x p y 1 q x q y 1   x   y ∣ = 0 \begin{vmatrix} 1\quad p_x\quad p_y\\ 1\quad q_x\quad q_y\\ 1\quad\ x\quad\ y \end{vmatrix}=0 ​1px​py​1qx​qy​1 x y​ ​=0
  不要忘了，这个行列式表示的是p、q构成的这条直线。

  那么还回到我们原来的问题上，点r在这条直线的哪一侧，那么：

• 在直线上：这个行列式=0
• 在直线的一侧：这个行列式>0
• 在直线的另一侧：这个行列式<0

算这样一个行列式的时间复杂度是$O(1)$。

  总之，我们知道了，对于一个点r，和p、q构成的直线而言，我们判断这个点在直线上，还是直线的哪一侧，只需做一件事：求这个行列式的值，看是等于0、小于0、大于0，就完事了。

  那么，有了这个概念，我们就可以想出一个解决凸包问题的蛮力法。

---

蛮力法

  对点集的任意两个点，我把它俩连成一条直线，然后我去判断其他所有的点是不是在这条直线的一侧。

n个点中任意取两个点，总共有$n(n-1)/2$中组合方式。

即，共计有$n(n-1)/2$根不同的线。

对于每一根线，我再去计算剩余的$n-2$个点是否均位于同一侧即可，即计算$n-2$个行列式的值。

  因此，蛮力法的时间复杂度是$O(n^3)$。

• 对于一个n个点的集合中的两个点$P_i$和$P_j$，当且仅当该集合中的其他点都位于穿过这两点的直线的同一边时它们的连线是该集合凸包边界的一部分。对每一对点都做一遍检验之后，满足条件的线段构成了该凸包的边界。
• 时间效率：$O(n^3)$。

分治法

  那我们不想用蛮力法，想优化一下，咋做呢。分治法呗。

• 分解：将集合S中的点按X轴坐标升序排列，用竖线将点集分成两个子集A和B。
• 求解：
  • 递归求解A的凸包；
  • 递归求解B的凸包。
• 合并：合并两个凸包。
• 注：凸包中的点用逆时针编号。

---

分解：

分治思想么。那肯定是把整个点集合S，分成两个子集合。

怎么分？那肯定是两个子集合分的比较平均、比较均匀为好。

取一个所谓的中间值？

按X轴取一个平均值？

——这会有一个问题：有些点的位置会很偏。

导致取平均值分出来的还是会不均匀。——就像我和马化腾、马云算平均工资一样。

那我们怎么样才能划分得比较均匀呢。

中位数。按X轴取中位数。

取中位数来划分的话，相对而言就比较均匀一些了。

那既然要按X轴的中位数来划分，那肯定要先排序。根据所有点的X坐标进行排序。

那对于排序，我们最快的排序算法是$O(nlogn)$。

那对于“分”，我们就解决怎么分的问题了，接下来研究怎么合并。

---

合并：

我们也总是在说，分治法思想，分开来很简单，合并比较不好合并。

那怎么来合并呢？

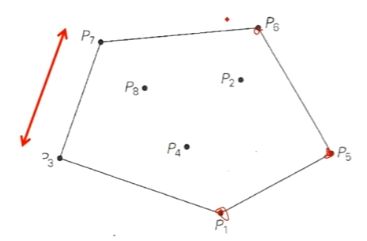
对于一个凸包，我们要对它的极点进行逆时针的编号。（如上面的图片所示：0、1、2、3、4、5、6）

我找到了左半边点集的凸包，也找到了右半边点集的凸包，我怎么把它俩进行合并呢？

• 找到最上面的切线和最下面的切线。
• 确定最终的凸包范围。（连起来，如上图的红线）

上切线、下切线的意思就是，这样一连接以后，所有的点都在它的下面、上面了。

问题是：如何寻找上、下切线？？

有人说，这还不简单，左边点集里面所有点，我找到y坐标最大的，右边也找到y轴最大的点，把它俩一连就行了。最低的同理。——貌似是这样的，起码对于上图而言，这样是可以的。

但是，我们再来看一个特殊的例子。

没毛病啊，这种情况完全有可能发生。我的两个子集也是遵循“按X轴坐标的中位数来划分”的。

这时候你去连接两个凸包中，各自y轴最小的点，就错了。

你说，那不取y坐标最高、最低了，我想办法去取最左、最右之类的？本质上也都是一个道理，总会有一些不符合的特殊情况，没办法真正解决问题。

  那到底咋弄呢？

---

寻找下切线

• 从A集合最右边的点和B集合最左边的点开始
• 如果这条线不是A和B的下切线，则：
  • 如果不是A的下切线，则逆时针旋转；
  • 如果不是B的下切线，则顺时针旋转。

啥叫下切线，就是对于你这根线而言，我所有的点都在你线的上面；

啥叫上切线，就是对于你这根线，我所有的点都在你的下面。

如图，我们先在A中找到最右边的一个，然后在B里找最左边的一个。

连成一根线，然后看这根线：

它这根线，是不是A的下切线，如果不是，我们再找下一个点（逆时针找）。

解释下逆时针是咋看的 ：

不要把目光放在区域A上，而要以这根线在凸包B的端点为中心，去看，是逆时针旋转，如上图所示。

先找找找找……找到凸包A的下切线，找到之后，再给B找。

给B找的时候，是顺时针旋转，怎么看顺时针，和上面一样的道理：以这条线位于凸包A上的端点为中心，去看顺时针旋转。

通过这种方式，下切线就能找出来了。

这也是为什么我们刚才说，对于一个凸包，我们要对它的极点逆时针来进行编号的原因。

如下图所示：

如此编上序号以后，我就可以进行所谓的“逆时针找”、“顺时针找”。

按照上面所说的步骤：

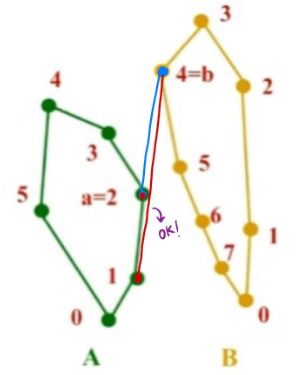
• 寻找A集合最右边的点a=2，寻找B集合最左边的点b=4。
• 如果这条线不是A和B的下切线，则：
  • 如果不是A的下切线，则逆时针旋转，即a=a-1，直到它暂时是A的下切线再停止；
  • 如果不是B的下切线，则顺时针旋转，即b=b+1，直到它暂时是B的下切线再停止。
  • 直到最终真正找到一条既是A的下切线、也是B的下切线的线，才最终停止。

如上图，它找下切线的过程如下所示：

1、初始时，a=2,b=4。

2、这条线不是A、B的下切线，首先，不是A的下切线，因此进行逆时针调整，如图，直到a=1，它是A的下切线，于是停止。

2、这条线不是A、B的下切线，此时它不是B的下切线，因此进行顺时针调整，如图，直到b=0，它是B的下切线，于是停止。

【注意】虽然刚才那条线已经是A的下切线，但是由于找B的下切线时所做的顺时针调整，此时这条线再次不是A的下切线了，因此还要继续调整。

3、这条线不是A、B的下切线，首先它不是A的下切线，因此进行逆时针调整，如图，直到a=0，它是A的下切线，于是停止。

4、此时依然做判断：这条线是不是A、B的下切线？——是。因此停止。

  于是最终找到了凸包A、B的下切线。

找到凸包A、B的下切线，时间复杂度为$O(n)$。

为啥是$O(n)$呢？我们判断一个直线是不是下切线，不是要看这个集合里所有的点吗？

在这里判断下切线，不必判断集合其余所有的点，而只需看和它相邻的极点就可以了。

比如下面这个图，对于a=4的时候，我需要调整b达到ab成为B的下切线，我咋看是不是B的下切线，我只需要看：

例如，对于a=4,b=10，是不是B的下切线——看a=4,b=9和a=4,b=11是否在它的同一侧即可。

例如，对于a=4,b=11，是不是B的下切线——看a=4,b=10和a=4,b=12是否在它的同一侧即可。

再另外举个例子，跟上面道理是一样的，自己看图体会下：

---

凸包问题运行时间分析

• 递归关系式：$T(n)=2T(n/2)+cn$
• 可最终推出：$T(n)=\theta (nlogn)$

这和我们最初的蛮力法$O(n^3)$相比，就好很多了。

---

对于凸包问题，有很多人给出了一些解决的算法，如下图。

插入一个小问题：棋盘覆盖问题

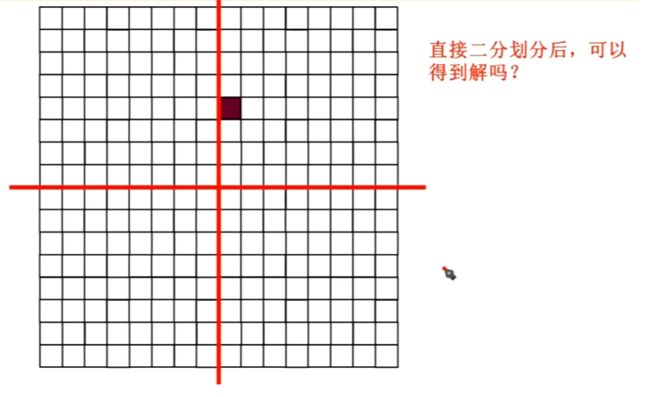
  直接把这个16×16的直接二分，能解决问题吗？——能解决那个带特殊方块的4×4的问题，但是其他的4×4，解决不了。

  再想一下我们分治法，进行二分，是基于什么原则：我们的二分，是把原问题分成两个与原问题相同类型的子问题才对。

  但是我们这样直接二分，分出来的子问题，就不是与原问题同类的问题了。

  那怎么处理？

  我在划分之前，先给中心的空白部分盖上一个L，然后再去进行划分。这样，我划分成的四个子块，就是同类问题（即，恰有一个方格不同）了。

（补的时候看好，给纯空白的地方补，如果已经有了1个了就不往他那里面补了）

第一次分解：

第二次分解：

第三次分解：

（四）二维最近对问题

简单来说，就是求：这么多点之内，到底哪两个点是距离最近的？

• $P_1(x_1,y_1),...,P_n(x_n,y_n)$是平面上$n$个点构成的集合$S$，假设$n=2^k$，最近点对问题要求找出距离最近的两个点。
• 最近点对问题是许多算法的基本步骤。

---

  我们用蛮力法来求解的话，其实就很好想了。不过多废话。

  怎么用分治法解决？

蛮力法

略。时间复杂度为$O(n^2)$。

分治法

  怎么划分呢？——这个其实在经过刚才对凸包的学习之后，也大概能想出来了。

  首先对所有点按照X轴进行升序排序，从中位数分开，分成两堆。（当然你按照Y轴也一样）

  分成两堆点的集合，之后干什么？

  我求左边这个子集合中，距离最近的；我求右边这个子集合中，距离最近的。

  分是这样分了，问题是还要把它俩合并起来。——仅仅合并这两边，是不够的，因为还有中间跨界的情况。

  那么这个跨界，我们就要解决它。跨界的情况怎么办？——先留着这个问题。

  如果先不管跨界的这个问题的话，我们就是一直分解分解……最后分解到什么情况了呢？每个子集合中只有两个点吗？——即使你的集合里只有两个点了，我还是要分解。——分解到每个子集合只含有1个点了，那此时合并这两个集合的时候，最小距离就是这两个点的距离。

---

  那再回来实际考虑清楚这个问题，我们求得左半边集合的最小距离d1了，也求得右半边集合的最小距离d2了，怎么合并起来，关键就在于我们如何求中间跨界问题。

---

咋办？

• 将点集$S$分为$S_1$和$S_2$，分隔线是$S$在$x$轴的中点。（问题：如何确定x=c？）
• 递归求解$S_1$和$S_2$的最近点对，令$d=min\{d_1,d_2\}$，确定$C_1$和$C_2$。（$C_1$和$C_2$就是下图中从中轴向左右两边画的那个虚线范围）
• 将$C_1$和$C_2$的最近点对合并。

先把点集划分为两个子集。

对左右两个子集，分别求出其最近点对的距离d1、d2。

中间跨界的怎么处理：取一个d，它为d1、d2中较小的那个距离。之后，从分界线x=c处，分别往左、右两边画出d的范围。

如果在画出的这个范围中，还能够找到有两个点，其距离小于d了（这一部分的点对距离，用暴力法），那么整个集合的最近点对就找到了。

有人说，那如果你的这些点分布的确实不均匀，上图虚线中的范围内，有非常多的结点。那这种情况下是否就和蛮力法区别不大了？——的确是这样的。

那怎么办？

实际上，在这个范围内的具体某一个点，它其实也不必去跟这个范围内的其余所有点进行两两比对，实际上它在上、下两个方向上距离d之内的范围去找就可以了。（光是Y轴坐标就已经差d了，何况还有可能是斜的？）

所以，基于此，我们发现，其实我们对所有点的Y轴坐标，也是要去做一个排序了。

---

二维最近对问题

• 在合并两个子集$C_1$和$C_2$时，对于$C_1$中的每个点$P(x,y)$，都需要检查$C_2$中的点和$P$之间的距离是否小于$d$。
• 假设$p$在$C_1$中，在$C_2$中与$p$距离小于$d$的点不会超过6个。
• 那么最多进行$6\ast n/2$次比较。

---

时间复杂度分析

合并最小问题所花的时间为$O(n)$。

该算法的最差递归时间为：$T(n)=2T(n/2)+n=O(nlogn)$。

---

分治法关键：

划分为小的同类的问题，然后合并。

分问题的步骤，一般不难；关键是在于合并。