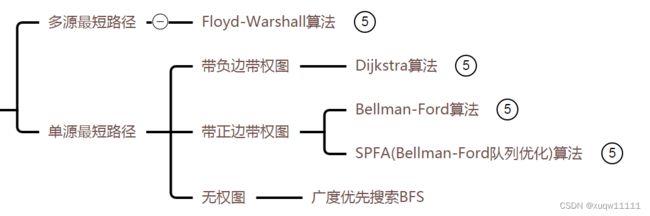
第五章 常用的最短路径算法
1、弗洛伊德算法(Floyd-Warshall)
问题描述:
上图中有4个城市8条公路,公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程,也就是求任意两个点之间的最短路径。这个问题也被称为“多源最短路径”问题。
构建邻接矩阵
直观思维解决问题
继续加入第3个点,第4个点。。。。。。。
#include
using namespace std;
int inf = 999999;
int e[4][4] = {{0, 2, 6, 4}, {inf, 0, 3, inf}, {7, inf, 0, 1}, {5, inf, 12, 0}};
int main() {
for (int v = 0; v < 4; v++)
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++) {
if (e[i][j] > e[i][v] + e[v][j])
e[i][j] = e[i][v] + e[v][j];
}
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
cout << e[i][j] << " ";
}
cout << endl;
}
return 0;
}
注意事项:
(1) Floyd算法可以解决带有负权边的图,但不能判断是否带有“负权回路”的图(带有负权回路的图是没有最短路径的)
(2) Floyd算法的时间复杂度为O(n^3),主要解决多源最短路径问题(任意两点之间的最短路径)。
2、狄克斯特拉算法(Dijkstra)
问题背景与定义
构建邻接矩阵
构建最短距离上界的估计值数组
问题求解过程
1号顶点所有出边进行松弛
2号顶点所有出边进行松弛
4号顶点所有出边进行松弛
3号顶点所有出边进行松弛
6号顶点所有出边进行松弛
总结:每次从所有没有进行选择的点中选择“估计值”最小的点,通过该点的所有出边对相连的点进行松弛操作,依次循环,直到所有顶点被选完为止。
主要过程:1、选点 2、出边松弛dis 3、1-2循环过程为n-1次(n为点的个数,最后一个点不再需要进行松弛操作)
问题程序实现
#include
using namespace std;
//邻接矩阵方式存储
int f = 9999;
//图的顶点数量与边数
int n = 6, m = 9;
int main() {
//初始化
//初始化邻接矩阵
int e[6][6] = {
{0, 1, 12, f, f, f},
{f, 0, 9, 3, f, f},
{f, f, 0, f, 5, f},
{f, f, 4, 0, 13, 15},
{f, f, f, f, 0, 4},
{f, f, f, f, f, 0}
};
//初始化dis数组
int dis[6] = {0, f, f, f, f, f};
//初始化book数组
int book[6] = {0};
int min_index = 0;
int min_dis = f;
//实现过程 总的循环过程 寻找n-1个点
for (int i = 0; i < n - 1; i++) {
//找点 次数寻找
min_dis = f;
for (int j = 0; j < n; j++) {
if (book[j] == 0 && dis[j] < min_dis) {
min_dis = dis[j];
min_index = j;
}
}
//标记点
book[min_index] = 1;
//找出边进行松弛操作
for (int j = 0; j < n; j++) {
if (e[min_index][j] < f && book[j] == 0) { //出边 且 没有找过该点
dis[j] = min(dis[j], dis[min_index] + e[min_index][j]); //松弛操作
}
}
//打印松弛过程
for (int d = 0; d < n; d++) {
cout << dis[d] << " ";
}
cout< 注意事项:
(1) Dijkstra算法无法解决带有负权边的图(在该算法每步松弛过程后认为找到的最短估计值已经是最短距离,如果后续还有点可以通过负边到达原来的点,使原来的点距离变得更短,那么后面做的工作就是不正确的了)。
(2) Dijkstra算法的时间复杂度为O(n^2),主要解决单源最短距离问题(由源点都任意一点之间的最短距离)。
(3) Dijkstra算法是使用明确边对最短路进行松弛操作,当边的数量远大于点的数量时,该算法可以实现较好的效果。
3、贝尔曼-福特算法(Bellman-Ford)
问题背景与定义
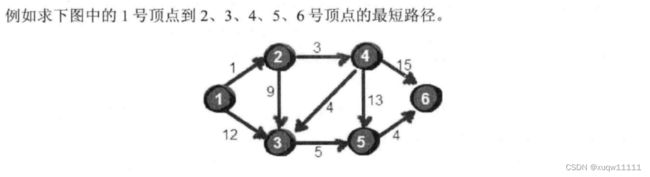
求下图中1号顶点到2、3、4、5号顶点的最短路径。
因为Bellman算法是使用边对所有顶点的估计值进行松弛操作,这里使用数组记录每条边的信息。
构建最短距离上界的估计值数组
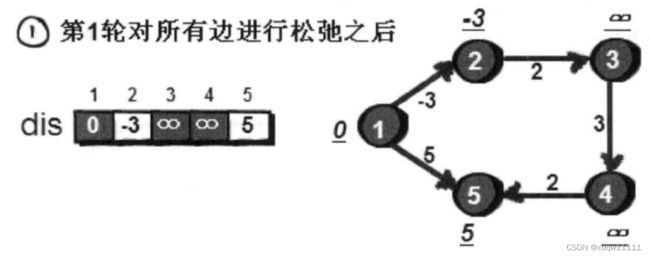
问题求解过程
总结:Bellman算法是对所有的边进行n-1次松弛操作,在前k个阶段结束后,就已经找出了从源点出发“最多经过k条边”达到各个顶点的最短路。直到进行完n-1个阶段后,便得到最多经过n-1条边的最短路。
问题代码实现
#include
using namespace std;
int n = 5, m = 5;
int u[5] = {2, 1, 1, 4, 3};
int v[5] = {3, 2, 5, 5, 4};
int w[5] = {2, -3, 5, 2, 3};
int main() {
//初始化dis数组
int f = 9999;
int dis[6] = {0, 0, f, f, f, f};
//松弛过程
for (int i = 0; i < n - 1; i++) { // 点数 |V-1|
for (int j = 0; j < m; j++) { // 边数 |E|
dis[v[j]] = min(dis[v[j]], dis[u[j]] + w[j]);
}
}
//输出结果
for (int i = 1; i <= n; i++) {
cout << dis[i] << " ";
}
return 0;
}
注意事项:
(1) Bellman算法可以解决带有负权边的图,(该算法是使用边对所有顶点进行松弛操作,而且操作的次数为n-1,可以优化起点到最远终点的最短距离)。
(2) Bellman算法的时间复杂度为O(mn),其中m为边的数量,n为点的数量, 主要解决单源最短距离问题(由源点都任意一点之间的最短距离)。
(3) Bellman算法可以判定是否存在环路。如果对于不存在负权回路的图进行n-1次松弛后就可以得到最短距离,后面再进行松弛,理论上不会影响所有最短距离,如果影响最短路说明存在负权回路。
int j = 0;
for (j = 0; j < m; j++) { // 边数 |E|
if(dis[v[j]]> dis[u[j]] + w[j]) break;
}
if(j==m) cout<<"存在负权回路";
else cout<<"不存在负权回路"4、贝尔曼-福特算法(Bellman-Ford) 队列优化(SPFA)
Bellman-Ford算法在每实施一次松弛操作后,就会有一些顶点已经求得其最短路,此后这些顶点的最短路的估计值就会一直保持不变,不再受后续松弛操作的影响,但是每次还要判断是否需要松弛,浪费时间,我们将优化上面的程序,实现“每次仅对最短路估计值发生变化了的顶点的所有出边进行松弛操作”。
问题背景与定义
求下图中1号顶点到2、3、4、5号顶点的最短路径。
dis来存放1号顶点到其余各个顶点的最短路径。初始时dis【1】为0,其余为无穷大。接下来将1号顶点入队。队列这里用一个数组que以及两个分别指向队列头和尾的变量head和tail来实现。
问题求解过程
弹出队列的顶点1,并使用顶点1的连边对相连顶点进行松弛操作,松弛成功的顶点入队
弹出队列的顶点2,并使用顶点2的连边对相连顶点进行松弛操作,松弛成功的顶点(该顶点在队列中不能存在)入队
在对2号顶点处理完毕后,需要将2号顶点出队,并依次对剩下的顶点做相同的处理,直到队列为空为止。最终数组 dis和队列 que状态如下:
(1) 初始化操作:可以使用邻接表或者邻接矩阵对点边进行数据存储,构建距离估计值数组dis,队列存在顶点标记数组book,构建队列,初始化队列标识与元素。
(2) 当队列不为空时循环进行松弛操作。
(3) 获取队列首顶点,使用连边对顶点进行松弛操作,松弛成功将对应,将对应顶点(判定队列中不存在)进行入队,所有连边处理完成后,首顶点出队,标记数组位清空。
(4) 打印1号顶点到所有顶点的最短距离。
问题代码实现
#include
using namespace std;
int u[101], v[101], w[101];
int First[101], Next[10001];
int _index = 0;
void add(int x, int y, int z) {
_index++;
u[_index] = x;
v[_index] = y;
w[_index] = z;
Next[_index] = First[x];
First[x] = _index;
}
int main() {
int n = 5, m = 7;
// cin >> n >> m;
//读取边到邻接表
// for (int i = 1; i <= m; i++) {
// cin >> u[i] >> v[i] >> w[i];
// Next[i] = First[u[i]];
// First[u[i]] = i;
// }
add(1,2,2);
add(1,5,10);
add(2,3,3);
add(2,5,7);
add(3,4,4);
add(4,5,5);
add(5,3,6);
//构建dis估计值数组和使用标识数组
int dis[101];
int book[101];
for (int i = 1; i <= n; i++) {
dis[i] = 9999;
book[i] = 0;
}
dis[1] = 0;
book[1] = 1;
//构建队列
int head = 1, tail = 1;
int que[101];
//将第一个点加入队列
que[tail] = 1;
tail++;
//进入循环,开始进行松弛操作
while (head != tail) {
int p = que[head];
int k = First[p];
//寻找连边进行松弛,加入队列
while (k != 0) {
if (dis[v[k]] > dis[u[k]] + w[k]) { //松弛成功
dis[v[k]] = dis[u[k]] + w[k];
if (book[v[k]] == 0) {
que[tail] = v[k];
tail++;
book[v[k]] = 1;
}
}
k = Next[k]; //寻找下一条边
}
book[head] = 0; //撤销标识
head++; //弹出队列
}
//打印最短距离
for (int i = 1; i <= n; i++) cout << dis[i] << " ";
return 0;
}
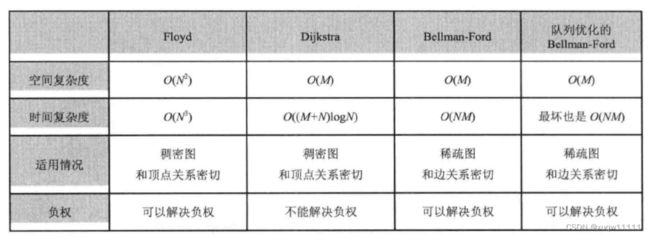
5、最短路径算法的对比分析
Floyd算法虽然总体时间复杂度高,但是可以解决负权边,并且均摊到每一点对上,在所有的算法中还是属于较优的。另外,Floyd算法较小的编码复杂度也是它的一大优势。所以,如果要求的是所有点对间的最短路径,或者如果数据范围较小,则Floyd算法比较适合。Diikstra算法最大的弊端是它无法适应有负权边的图。但是Diikstra具有良好的可扩展性,扩展后可以适应很多问题。另外用堆优化的Dijkstra算法的时间复杂度可以达到O(Mlog(N))。当边有负权时,需要使用 Bellman-Ford算法或者队列优化的 Bellman-Ford算法。因此我们选择最短路径算法时,要根据实际需求和每一种算法的特性,选择适合的算法。
图的邻接表数组表示
#include
using namespace std;
const int N = 1010;
const int M = 10100;
int v[M], w[M];
int _first[N], _next[M];
int i = 0;
void add(int _u, int _v, int _w) { //加入一条边
i++;
v[i] = _v;
_next[i] = _first[_u];
_first[_u] = i;
w[i] = _w;
}
void printU(int _u) {
//访问从_u出发的所有边,遍历的代码如下,当_next[i]为0时遍历结束
for (int i = _first[_u]; i; i = _next[i]) {
int _v = v[i];
int _w = w[i];
cout << _u << "," << _v << "," << _w << endl;
}
}
int main() {
add(1,2,77);
add(2,3,777);
add(2,5,77777);
add(3,5,77777);
add(5,4,7777);
add(5,1,7);
for(int k=1;k<=5;k++){
cout<