字符串哈希值
文章目录
-
- LC-2156 查找给定哈希值的子串
-
- 字符串哈希算法:
- LC-187 重复的DNA序列
-
- 解法1:哈希
- 解法2:位运算【官方题解】
- 解法3:字符串哈希
- LC-1044 最长重复子串
- 字符串哈希
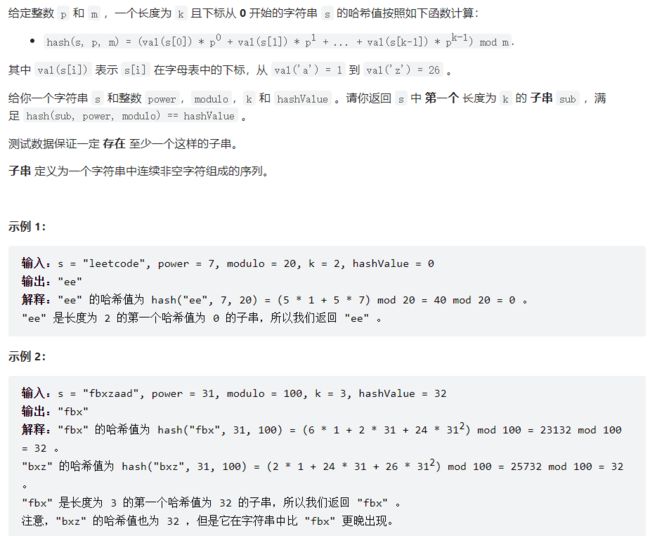
LC-2156 查找给定哈希值的子串
解法:为长度为k的每一个连续字符串计算哈希值。而长度为k的窗口滑动过程中,两个相邻的字符串哈希值计算是有规律的。
记H(s,i,p) = s[i]*P^0 + s[i+1]*P^1 + … + s[i + k - 1]*P^(k - 1);
则H(s,i+1,p) = s[i+1]*P^0 + s[i+2]*P^1 + … + s[i + k - 1]*P^(k - 2) + s[i + k]*P^(k-1);
有关系:H(s,i,p) = P*H(s,i + 1, p) + s[i] - s[i+k]*P^(k);
或者H(s,i,p) = P*(H(s,i+1,p) - s[i+k]*P(k-1)) + s[i];
-
注意:
-
题目中需要对modulo取余,故对于int型的变量,要注意转为long类型的操作。
-
此外,h(s,i+1,P)是取余后的结果,在减去s[i+k]*P(k-1)该项时可能会出现负数,需要做一个加modulo的处理。
-
字符串哈希算法:
class Solution {
public String subStrHash(String str, int power, int modulo, int k, int hashValue) {
int multi = 1; // 记录 k-1 次方 % modulo
int n = str.length();
int pos = -1; // 第一个符合要求子串的起始位置
int h = 0; // 子串哈希值
for (int i = n - 1; i >= n - k; i--) {
int value = str.charAt(i) - 'a' + 1;
h = (int) (((long) h * power % modulo + (long)value) % modulo);
if (i != n - k){ // multi 是k-1次方
multi = (int) ((long) multi * power % modulo);
}
}
if (h == hashValue) {
pos = n - k;
}
System.out.println(multi);
// 从后向前找
for (int i = n - k - 1; i >= 0; i--) {
int valueI = str.charAt(i) - 'a' + 1;
int valueK = str.charAt(i + k) -'a' + 1;
h = (int) ((( h - (long) valueK * multi % modulo + modulo) * (long)power + (long)valueI) % modulo);
if (h - hashValue == 0) {
pos = i;
}
}
return str.substring(pos, pos + k);
}
}
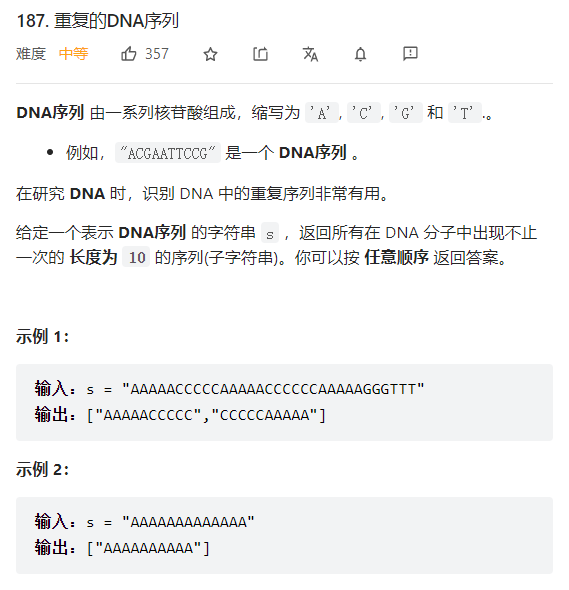
LC-187 重复的DNA序列
解法1:哈希
class Solution {
static final int L = 10;
public List<String> findRepeatedDnaSequences(String s) {
List<String> ans = new ArrayList<String>();
Map<String, Integer> cnt = new HashMap<String, Integer>();
int n = s.length();
for (int i = 0; i <= n - L; ++i) {
String sub = s.substring(i, i + L);
cnt.put(sub, cnt.getOrDefault(sub, 0) + 1);
if (cnt.get(sub) == 2) {
ans.add(sub);
}
}
return ans;
}
}
解法2:位运算【官方题解】
https://leetcode-cn.com/problems/repeated-dna-sequences/solution/zhong-fu-de-dnaxu-lie-by-leetcode-soluti-z8zn/
A:0 即 00, C:1 即01, G:2 即 10,T:3 即 11. 都可以统一用两位01二进制表示。
而题目要求,寻找长度为10的重复子序列。长度为10则最多需要20个二进制位,故int类型的32位可以容纳该序列。
窗口向右移动一格,
- 则变量左移2格再与0(或1或2或3)进行或操作,加入到变量中。
- 变量与低20位全为1的数做与操作。对低20位的的数进行保留,同时将高12位置0. 具体操作为和(1左移20位再减一)的数进行与操作。
- 将变量加入hashMap中。
class Solution {
static final int L = 10;
Map<Character, Integer> bin = new HashMap<Character, Integer>() {{
put('A', 0);
put('C', 1);
put('G', 2);
put('T', 3);
}};
public List<String> findRepeatedDnaSequences(String s) {
List<String> ans = new ArrayList<String>();
int n = s.length();
if (n <= L) {
return ans;
}
int x = 0;
for (int i = 0; i < L - 1; ++i) {
x = (x << 2) | bin.get(s.charAt(i));
}
Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();
for (int i = 0; i <= n - L; ++i) {
x = ((x << 2) | bin.get(s.charAt(i + L - 1))) & ((1 << (L * 2)) - 1);
cnt.put(x, cnt.getOrDefault(x, 0) + 1);
if (cnt.get(x) == 2) {
ans.add(s.substring(i, i + L));
}
}
return ans;
}
}
解法3:字符串哈希
https://mp.weixin.qq.com/s/ER7ud9Q9sZIb7qQvC_Gj0w
| 字符索引 | i | p[i] | h[i] |
|---|---|---|---|
| 0 | 1 | P^1 | s[0]*p^0 |
| 1 | 2 | P^2 | s[0]*p1+s[1]*p0 |
| 2 | 3 | P^3 | s[0]*p2+s[1]*p1+s[2]*p^0 |
| 3 | 4 | P^4 | s[0]*p3+s[1]*p2+s[2]*p1+s[3]*p0 |
| 4 | 5 | P^5 | s[0]*p4+s[1]*p3+s[2]*p2+s[3]*p1+s[4]*p^0 |
| 5 | 6 | p^6 | s[0]*p5+s[1]*p4+s[2]*p3+s[3]*p2+s[4]*p1+s[5]*p0 |
例:长度为3.
则 i = 1时,从字符0到2这段字符串的hash值为,hash=h[3]-h[0]*p3=s[0]*p2+s[1]*p1+s[2]*p0.
i = 2 时, 从字符1到3这段字符串的hash值为, hash=h[4]-h[1]*p3=s[1]*p2+s[2]*p1+s[3]*p0.
…
class Solution {
int N = (int)1e5+10, P = 131313;
int[] h = new int[N], p = new int[N];
public List<String> findRepeatedDnaSequences(String s) {
int n = s.length();
List<String> ans = new ArrayList<>();
p[0] = 1;
for (int i = 1; i <= n; i++) {
h[i] = h[i - 1] * P + s.charAt(i - 1);
p[i] = p[i - 1] * P;
}
Map<Integer, Integer> map = new HashMap<>();
for (int i = 1; i + 10 - 1 <= n; i++) {
int j = i + 10 - 1;
int hash = h[j] - h[i - 1] * p[j - i + 1];
int cnt = map.getOrDefault(hash, 0);
if (cnt == 1) ans.add(s.substring(i - 1, i + 10 - 1));
map.put(hash, cnt + 1);
}
return ans;
}
}
LC-1044 最长重复子串
字符串哈希
https://mp.weixin.qq.com/s/-zFkbOGEx2YJYzQopDkYiw
| 字符索引 | i | p[i] | h[i] |
|---|---|---|---|
| 0 | 0 | 1 | s[0]*p^0 |
| 1 | 1 | P^1 | s[0]*p1+s[1]*p0 |
| 2 | 2 | P^2 | s[0]*p2+s[1]*p1+s[2]*p^0 |
| 3 | 3 | P^3 | s[0]*p3+s[1]*p2+s[2]*p1+s[3]*p0 |
| 4 | 4 | P^4 | s[0]*p4+s[1]*p3+s[2]*p2+s[3]*p1+s[4]*p^0 |
| 5 | 5 | P^5 | s[0]*p5+s[1]*p4+s[2]*p3+s[3]*p2+s[4]*p1+s[5]*p0 |
- 以2开始,长度为3时。i=2,j=4; 该哈希值计算方法为,h[4]-h[1]*P^3。相减后,需要保留3项,而h[4]含s[4]且为5项,需减去长度为2项的h[1].
class Solution {
long[] h, p;
public String longestDupSubstring(String s) {
int P = 1313131, n = s.length();
h = new long[n + 10]; p = new long[n + 10];
p[0] = 1;
for (int i = 0; i < n; i++) {
p[i + 1] = p[i] * P;
h[i + 1] = h[i] * P + s.charAt(i);
}
String ans = "";
int l = 0, r = n;
while (l < r) {
int mid = l + r + 1 >> 1;
System.out.println(mid);
String t = check(s, mid);
if (t.length() != 0){
l = mid; // 找到了,长度增加
} else {
r = mid - 1; // 没找到,长度减少
}
ans = t.length() > ans.length() ? t : ans;
}
return ans;
}
public String check(String s, int len) {
int n = s.length();
Set<Long> set = new HashSet<>();
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1;
long cur = h[j] - h[i - 1] * p[j - i + 1];
if (set.contains(cur)){
return s.substring(i - 1, j);
}
set.add(cur);
}
return "";
}
}