LeetCode 第 228 场周赛

5676. 生成交替二进制字符串的最少操作数

题意：
给你一个仅由字符 ‘0’ 和 ‘1’ 组成的字符串 s 。一步操作中，你可以将任一 ‘0’ 变成 ‘1’ ，或者将 ‘1’ 变成 ‘0’ 。

交替字符串 定义为：如果字符串中不存在相邻两个字符相等的情况，那么该字符串就是交替字符串。例如，字符串 “010” 是交替字符串，而字符串 “0100” 不是。

返回使 s 变成 交替字符串 所需的 最少 操作数。

思路
最后的交替字符串不是010101就是10101010，所以构造这两个母串，和原字符串对比取最小不同数量的即可。
代码

class Solution {
public:
    int minOperations(string s) {
        int len=s.size();
        int ans=0;
        string s1="";
        string s2="";
        int f=0;
        for(int i=0;i

1759. 统计同构子字符串的数目

题意

给你一个字符串 s ，返回 s 中 同构子字符串 的数目。由于答案可能很大，只需返回对 109 + 7 取余 后的结果。

同构字符串 的定义为：如果一个字符串中的所有字符都相同，那么该字符串就是同构字符串。

子字符串 是字符串中的一个连续字符序列。

思路
扫一遍原串，统计连续相等的个数，求和取余即可。
代码

class Solution {
public:
    int countHomogenous(string s) {
        int len=s.size();
        long long int ans=0;
        long long int mod=1000000007;
        for(int i=0;i

1760. 袋子里最少数目的球

题意
给你一个整数数组 nums ，其中 nums[i] 表示第 i 个袋子里球的数目。同时给你一个整数 maxOperations 。

你可以进行如下操作至多 maxOperations 次：

选择任意一个袋子，并将袋子里的球分到 2 个新的袋子中，每个袋子里都有 正整数 个球。
比方说，一个袋子里有 5 个球，你可以把它们分到两个新袋子里，分别有 1 个和 4 个球，或者分别有 2 个和 3 个球。
你的开销是单个袋子里球数目的 最大值 ，你想要 最小化 开销。

请你返回进行上述操作后的最小开销。

思路
二分最后的答案最小开销ans，若所有数都能变成当前的答案则满足：
每个数的开销等于num[i]/ans
总开销即为相加即可得到

注：-1是为了避免相同的情况

代码

class Solution {
public:

    bool ok(vector&nums,int x,int n){
        int op=0;
        for(int i=0;in) return false;
        }
        return op<=n;
    }

    int minimumSize(vector& nums, int n) {

        int l=1,r=1000000000,ans=0;
        //二分最后的答案
        while(l<=r) {
            int mid=(l+r)/2;
            if(ok(nums,mid,n)) {
                r=mid-1;
                ans=mid;
            }
            else l=mid+1;
        }
        return ans;
    }
};

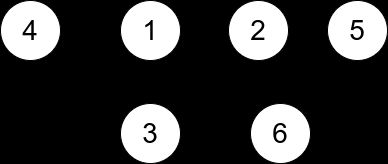
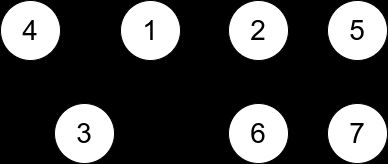
1761. 一个图中连通三元组的最小度数

给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [ui, vi] ，表示 ui 和 vi 之间有一条无向边。

一个 连通三元组 指的是 三个 节点组成的集合且这三个点之间 两两 有边。

连通三元组的度数 是所有满足此条件的边的数目：一个顶点在三元组内，而另一个顶点不在三元组内。

请你返回所有连通三元组中度数的 最小值 ，如果图中没有连通三元组，那么返回 -1 。

示例 1：

输入：n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
输出：3
解释：只有一个三元组 [1,2,3] 。构成度数的边在上图中已被加粗。

示例 2：

输入：n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
输出：0
解释：有 3 个三元组：
1) [1,4,3]，度数为 0 。
2) [2,5,6]，度数为 2 。
3) [5,6,7]，度数为 2 。

思路
利用并查集找出连通块，然后将每个联通块内的点存进vector中，遍历所有连通块，对连通块内部的点进行枚举，枚举一个联通三元组，同时预处理出与每个点相连的点的个数，相加计算答案即可。

代码

class Solution {
public:
    
    int f[10005];
    int d[10005];
    int b[10005];
    vectora[1005];
    vectorbb[1005];
    int m[405][405];
    int find(int x){
        if(x!=f[x]) f[x]=find(f[x]);
        return f[x];
    }
    
    int minTrioDegree(int n, vector>& mp) {
        //模拟连通块
        
        for(int i=1;i<=n;i++) {
            f[i]=i;
            d[i]=1;
        }
        int len=mp.size();
        for(int i=0;i=3) {
               // cout<