前缀和（一维、二维）c++实现

代码实现中我使用的头文件是，如果运行不成功请注意更换。

一维前缀和

是什么？

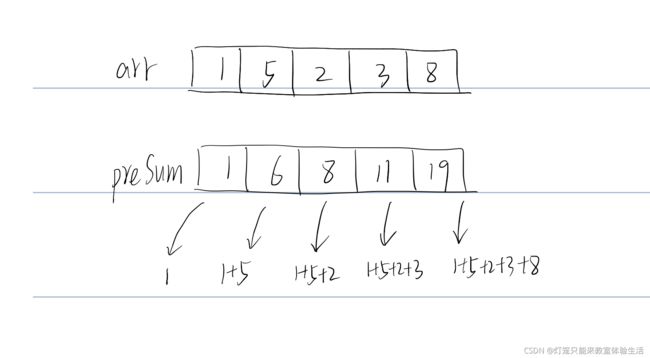
一个数组中，从【第一个元素】到【当前元素】的【数值和】，通常简写为preSum

有什么用？

能够快速查询一个数组中[L,R]范围内的【数值和】。

怎么用？

根据前缀和的定义，preSum[index]就是从数组在[0,index]范围上的【数值和】。

• preSum[R] = arr[0] + arr[1] + … + arr[L] + … + arr[R]

• preSum[R] = arr[0] + arr[1] + … + arr[L]

• 所以[L,R]上的数值和就是 ：preSum[R]-preSum[L-1]。

• 要注意数组是否越界。
  
  
  
  
  
  

代码实现

输入的数据从1开始，而非0

#include 
using namespace std;
/*
输入组长度为 n 的数据，查询 数组中 [L,R] 上的和

input:
5 3
2 1 3 6 4
1 2
1 3
2 4


output:
3
6
10

*/
void getPreSumArray(vector<int> &arr){
    for(int i=1;i<arr.size();i++){
        arr[i]=arr[i-1]+arr[i];
    }
}
int getScopeSum(vector<int> &arr,int L,int R){
    return L-1>=0?arr[R]-arr[L-1]:arr[R];
}
void solution(){
    int m,n;//m组查询数据，长度为n的数组
    cin>>n>>m;
    vector<int> arr;
    for (int i = 0; i < n; ++i){
        int tmp;
        cin>>tmp;
        arr.push_back(tmp);
    }
    getPreSumArray(arr);
    while(m--){
        int L,R;
        cin>>L>>R;
        cout<<getScopeSum(arr,L-1,R-1)<<endl;
    }
}
int main(){
    solution();
    return 0;
}

---

二维前缀和

是什么？

一个二维数组中，从【第一个元素】到【当前元素】范围内的【数值和】

有什么用？

给定【起点坐标】和【终点坐标】，能够快速查询两点范围内的【数值和】

怎么用？

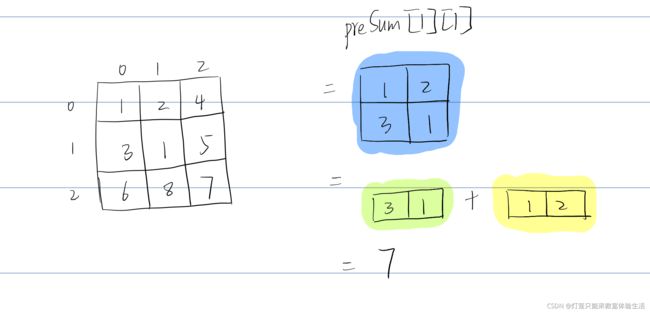
以上图举例：

• 对于某一行，比如第一行，【数值和】其实就是一维的前缀和，这个很好理解。

• 对于多行，比如前两行，相当于当前行的【一维前缀和】+上一行的一维【前缀和】。

  举个例子：
  

• 注意，不要纠结preSum[1][1]到底是哪一个，我们只关注原理。
  

• 此时再看看：起点为[1,1]，终点为[2,2]的数值和
  
  很清晰了：
  假设：行为x轴，列为y轴，起点为(x1,y1)，终点为(x2,y2)。
  那起点到终点的数值和就是：
  result = preSum[x2][y2] - preSum[x2][y1-1] - preSum[x1-1][y2] + preSum[x1-1][y1-1]
  当然，要注意数组越界问题。

代码实现

输入的坐标原点是(1,1)，符合用户直觉，而非(0,0)

/*
 * 给定【起点坐标】和【终点坐标】返回两点范围内的【数值和】
 *
 * */
#include 
using namespace std;
void inputMatrix(vector<vector<int>> &preSum,int n,int m){
    for(int i=0;i<n;i++){
        vector<int> tmpVector;
        for(int j=0;j<m;j++){
            int tmp;
            cin>>tmp;
            tmpVector.push_back(tmp);
        }
        preSum.push_back(tmpVector);
    }
}
void initMatrix(vector<vector<int>> &preSum){
    int row = preSum.size();
    int col = preSum[0].size();
    for(int i=0;i<row;i++){
        for(int j=0;j<col;j++){
            int p1 = 0;
            int p2 = 0;
            if(j-1>=0)p1 = preSum[i][j-1];
            if(i-1>=0)p2 = preSum[i-1][j];
            if(p1&&p2)preSum[i][j]-=preSum[i-1][j-1];
            preSum[i][j]+=p1+p2;
        }
    }
}
int getScopeSum(vector<vector<int>> &preSum, int x1, int y1, int x2, int y2){
    int p1 = 0;
    int p2 = 0;
    int p3 = 0;
    if(y1-1>=0)p1=preSum[x2][y1 - 1];
    if(x1-1>=0)p2=preSum[x1 - 1][y2];
    if(p1&&p2)p3=preSum[x1 - 1][y1 - 1];
    return preSum[x2][y2] - p1 - p2 + p3;
}
void solution(){
    int n,m,T;//n行m列的矩阵，T次查询
    cin>>n>>m>>T;
    vector<vector<int>> matrix;
    inputMatrix(matrix,n,m);
    initMatrix(matrix);
    while(T--){
        int x1,x2,y1,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<getScopeSum(matrix,x1-1,y1-1,x2-1,y2-1)<<endl;
    }
}
/*
input:
3 3 3
1 3 6
2 5 4
8 7 9

1 1 2 2
1 1 3 3
2 2 3 3

output:
11
45
25
 */
int main(){
    solution();
    return 0;
}