- 我们大多在食用二次知识――论知识的阶级性
Yo有灵L0
不论是《美丽新世界》,还是《未来简史》,对人类未来的预计都没有很美好。这其中包含了太多集权的观点。即:人类的绝大多数资源被极少数人所掌控,而绝大多数人沦为平庸。在《美丽新世界》里,阶级的划分直接由人为控制出生来决定;在《未来简史》里,当人们把越来越多的事情交给算法去处理之后,人类自身则降至被动的地位。这些看起来和知识不搭边?不,知识这条路,竟然也存在着阶级划分。这种阶级划分,有自身的因素,也有环境
- Python游戏开发实战:打造高仿俄罗斯方块掌机坦克大战
引言在那个电子游戏刚刚兴起的年代,俄罗斯方块掌机上的坦克大战承载着无数玩家的童年记忆。简单的像素画面、紧张刺激的战斗、精准的操作反馈,这些元素构成了一个经典的游戏体验。今天,我们将用Python和pygame库来重新诠释这个经典游戏,不仅要还原其精髓,更要在技术实现上进行创新和优化。这个项目不仅仅是一个简单的游戏复刻,更是一次完整的游戏开发实践。从游戏架构设计到用户体验优化,从碰撞检测算法到动态难
- 【华为od刷题(C++)】HJ89 24点运算
m0_64866459
华为odc++开发语言
我的代码:#include//包含了如排序、排列等常用算法#include//用于输入输出操作#include//无序映射,用于将扑克牌的字符映射到对应的数字#include//动态数组,用于存储输入的扑克牌usingnamespacestd;charops[4]={'+','-','*','/'};//这是一个操作符数组,包含了四个基本的数学运算符:加、减、乘、除unordered_mapmap
- 揭秘FloodFill算法:图像填充利器
KENYCHEN奉孝
python实践大全算法python开发工具
FloodFill算法概述FloodFill是一种用于填充连通区域的算法,常用于图像处理、绘图工具(如“油漆桶”工具)和迷宫求解等场景。其核心思想是从一个起始点出发,向四周(四邻域或八邻域)扩展,直到遇到边界或满足停止条件。算法原理连通性定义:根据需求选择四邻域(上、下、左、右)或八邻域(包含对角线方向)作为填充方向。边界条件:填充需在指定区域内进行,遇到边界颜色或特定标记时停止。实现方法递归实现
- 【算法300题】:双指针
双指针板块925.长按键入leetcode链接你的朋友正在使用键盘输入他的名字name。偶尔,在键入字符c时,按键可能会被长按,而字符可能被输入1次或多次。你将会检查键盘输入的字符typed。如果它对应的可能是你的朋友的名字(其中一些字符可能被长按),那么就返回True。思路这道题目只要是末尾的边界条件比较恶心一点classSolution{public:boolisLongPressedName
- 算法:floyd和高精度 洛谷 最短路 P1037 [NOIP 2002 普及组] 产生数
健仙
算法算法数据结构c++
思路:因为某个数变成另一个数是单向的,并且一个数变成另一个数后还可以变,让我联想到图论的内容,一个数变成其他数就相当于这个数与另一个数有单向边,而且边之间的线路可以让一个数可能变成很多数,因为数据量很小,我就想到了floyd,就是我们用floyd做传递闭包,得出一个数可以变成哪些数,然后将每个位看一遍,乘起来就是答案,不过这里有个小坑,答案超过了2的64次方,所以还要高精度算法处理一下。代码:#i
- 算法:动态规划 洛谷 P8776 [蓝桥杯 2022 省 A] 最长不下降子序列
健仙
算法动态规划蓝桥杯
思路:首先,这题你得先会(nlogn)复杂度的求最长不下降子序列方法。我们可以直接让k个数从下标为1开始,滑动到末端,这k个数就不用看它,因为我们把他设置成k个数后面的数,所以答案先加上k,然后我们看预处理每一个数从他开始(包括这个数)后面的最长不下降子序列,把长度放入b数组中,这样我们答案就是k加上b【k+1】,然后我们看k前面的数,k前面的数不是让答案加上前面的最长不下降子序列,因为此时我们有
- 算法竞赛备赛——【图论】求最短路径——Floyd算法
Aurora_wmroy
算法竞赛备赛算法图论c++蓝桥杯数据结构
floyd算法基于动态规划应用:求多源最短路时间复杂度:n^3dijkstra:不能解决负边权floyd:能解决负边权不能解决负边权回路问题求最短路径:dijkstrabfsfloyd思路1.让任意两点之间的距离变短:引入中转点k通过k来中转i---->k---->jj2.找状态:n个点都可以做中转点的情况下,i到j之间的最短路径的长度是x最终状态:dp[n][i][j]=x;中间状态:dp[k]
- 《[系统底层攻坚] 张冬〈大话存储终极版〉精读计划启动——存储架构原理深度拆解之旅》-系统性学习笔记(适合小白与IT工作人员)
谢郎Kobe
大活存储学习架构云计算硬件架构大数据
致所有存储技术探索者笔者近期将系统攻克存储领域经典巨作——张冬老师编著的《大话存储终极版》。这部近千页的存储系统圣经,以庖丁解牛的方式剖析了:存储硬件底层架构、分布式存储核心算法、超融合系统设计哲学等等。喜欢研究数据存储或者工作应用到存储的小伙伴,可以学习这本书。如果想利用碎片时间学习,也可以持续关注一下笔者不定期的章节解析。现在本人将此书的目录结构整理如下,未来笔者将按照顺序不定期更新【学习笔记
- 颠覆性的货币时代来了!千城攻略“主权资产货币系统”面世
笔记侠
2020年7月7日,深圳千城攻略算法云技术有限公司与重塑布雷顿森林体系委员会云签约,成为面向央行提供服务的主权货币技术核心成员。重塑布雷顿森林委员会执行董事MarcUzan先生、千城攻略首席算法官郑志军先生出席签约仪式。与比特币、Libra完全不一样,千城攻略颠覆了长期以来根深蒂固的“主权信用货币”体制观念,推出了“主权资产货币”,由于其有着非常严谨科学的全新经济学理论和货币理论系统支撑,并且解决
- 【机器学习】必会降维算法之:独立成分分析(ICA)
Carl_奕然
机器学习算法人工智能
独立成分分析(ICA)1、引言2、独立成分分析(ICA)2.0引言2.1定义2.2应用场景2.3核心原理2.4实现方式2.5算法公式2.6代码示例3、总结1、引言小屌丝:鱼哥,最近胡塞武装很哇塞啊。小鱼:你什么时候开始关注军事了?小屌丝:这…还用关注吗?都上新闻了。小鱼:嗯,那你知道胡塞武装为什么这么厉害吗?小屌丝:额…当然是光脚不怕穿鞋的。小鱼:…你可真是…小屌丝:真是啥?小鱼:一个字,自己体会
- MATLAB最优滤波器设计函数firpm的使用详解
codersnote
编程小识matlab算法最优滤波器firpmkaiserord
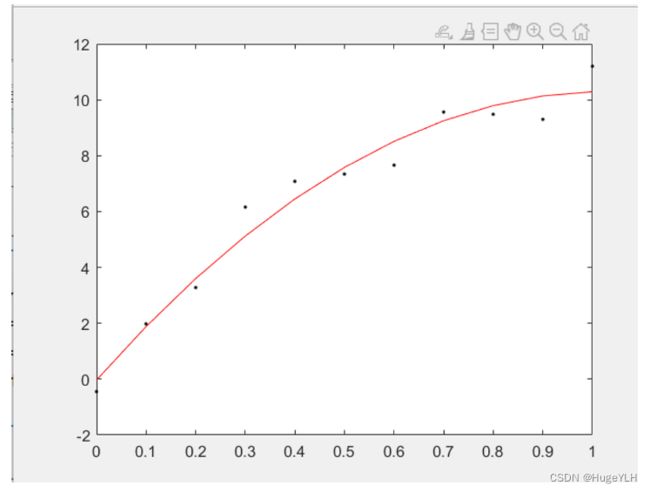
窗函数法设计的缺点无法选择过渡带、通带、阻带衰减等指标阶数不是最优的凯塞窗[n,wn,beta,ftype]=kaiserord(f,a,dev);h_kaiser=fir1(n,wn
- 数字滤波器原理及应用 借助matlab,数字滤波器原理及应用(借助Matlab)
陈慈龙
数字滤波器原理及应用借助matlab
第l章数字信号处理引言1.1引言1.2数字信号处理起源1.3信号域1.4信号分类1.5DStP:一个学科第2章采样原理2.1引言2.2第l章数字信号处理引言1.1引言1.2数字信号处理起源1.3信号域1.4信号分类1.5DStP:一个学科第2章采样原理2.1引言2.2香农采样原理2.3信号重构2.4香农插值2.5采样方法2.6多通道采样2.7MATLAB音频选项第3章混叠3.1引言3.2混叠3.3
- ica算法c语言,独立成分分析(ICA)的模拟实验(R语言)
weixin_39632212
ica算法c语言
本笔记是ESL14.7节图14.42的模拟过程。第一部分将以ProDenICA法为例试图介绍ICA的整个计算过程;第二部分将比较ProDenICA、FastICA以及KernelICA这种方法,试图重现图14.42。ICA的模拟过程生成数据首先我们得有一组独立(ICA的前提条件)分布的数据$S$(未知),然后经过矩阵$A_0$混合之后得到实际的观测值$X$,即$$X=SA_0$$也可以写成$$S=
- 列梅兹remez算法求解最佳一致逼近多项式(C语言实现)
landcruiser007
计算方法计算方法数值分析列梅兹算法
//remzf.h//实现remez算法#include#includevoidremz(a,b,p,n,eps,f)intn;doublea,b,eps,p[],(*f)(double);{inti,j,k,m;doublex[21],g[21],d,t,u,s,xx,x0,h,yy;if(n>20)n=20;//逼近多项式的最高次数为19m=n+1;d=1.0e+35;for(k=0;k<=n
- Java数据结构与算法(爬楼梯动态规划)
盘门
java数据结构与算法实战java动态规划开发语言
前言爬楼梯就是一个斐波那契数列问题,采用动态规划是最合适不过的。实现原理初始化:dp[0]=1;dp[1]=2;转移方程:dp[i]=dp[i-1]+d[i-2];边界条件:无具体代码实现classSolution{publicintclimbStairs(intn){if(n==1){return1;}int[]dp=newint[n];dp[0]=1;dp[1]=2;for(inti=2;i<
- 搜索插入位置
AWEN_33
算法leetcode数据结构
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。请必须使用时间复杂度为O(logn)的算法(二分法)。classSolution{public:intsearchInsert(vector&nums,inttarget){//初始化二分查找的边界://low:左边界,从数组起始位置开始(索引0)//high:右边界,从数组最后
- c语言学习15四则运算
四则运算练习需求:进入一个界面选择+-*/printf选择运算法则(如果选择错误,提示重新选择)switchcasedefult显示100以内两个随机数,输入运算结果rand系统显示正确答案,并且判断正确错误要求:封装函数分析:intmain(void){//界面程序-----界面函数//输入和识别程序-----按键识别函数//随机数程序----产生随机数函数//系统计算并且对比答案----对比答
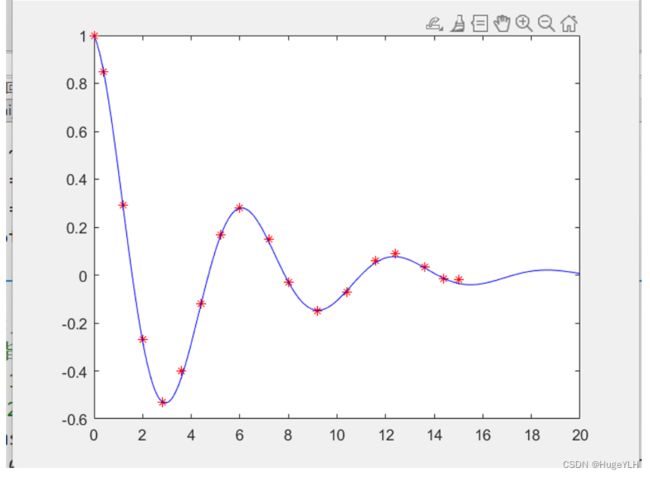
- 雷米兹交换算法(Remez Exchange Algorithm)的数学理论
雷米兹交换算法(RemezExchangeAlgorithm)的数学理论引言雷米兹交换算法(RemezExchangeAlgorithm)是数值逼近理论中的核心算法,其理论基础建立在19世纪切比雪夫(Chebyshev)的开创性工作之上。第一章切比雪夫逼近的理论基础1.1切比雪夫多项式的定义与性质第一类切比雪夫多项式Tn(x)T_n(x)Tn(x)在区间[−1,1][-1,1][−1,1]上通过如
- 【从零开始的LeetCode-算法】3202. 找出有效子序列的最大长度 II
九圣残炎
算法leetcodejava
给你一个整数数组nums和一个正整数k。nums的一个子序列sub的长度为x,如果其满足以下条件,则称其为有效子序列:(sub[0]+sub[1])%k==(sub[1]+sub[2])%k==...==(sub[x-2]+sub[x-1])%k返回nums的最长有效子序列的长度。示例1:输入:nums=[1,2,3,4,5],k=2输出:5解释:最长有效子序列是[1,2,3,4,5]。示例2:输
- 剑指offer66_不用加减乘除做加法
不用加减乘除做加法写一个函数,求两个整数之和,要求在函数体内不得使用+、-、×、÷四则运算符号。数据范围输入和输出都在int范围内。样例输入:num1=1,num2=2输出:3算法思路这是一个不使用加减运算符实现整数加法的算法,利用了位运算来模拟加法过程。核心思想是将加法分解为:无进位相加(通过异或运算^实现)计算进位(通过与运算&和左移<<实现)循环直到进位为0时间复杂度:O(1)因为整数位数固
- java实现多表代替密码(维吉尼亚密码)
就问你爱信不信
维基利亚密码java密码加密解密密码学加密解密java算法
维吉尼亚密码(又译维热纳尔密码)是使用一系列凯撒密码组成密码字母表的加密算法,属于多表密码的一种简单形式。设d为一固定的正整数,d个位移代换表π=(π1,π2,…,πd),由密钥序列K=(k1,k2,…,kd)给定,第i+td个明文字母由表πi决定。即密钥ki决定加密算法如下:ek(xi+td)=(xi+td+ki)mod(q)e_k(x_{i+td})=(x_{i+td}+k_i)mod(q)e
- MTALAB实现多表代替密码(维吉尼亚密码)
就问你爱信不信
matlab加密解密维吉尼亚密码密码学加密解密算法matlab
维吉尼亚密码(又译维热纳尔密码)是使用一系列凯撒密码组成密码字母表的加密算法,属于多表密码的一种简单形式。设d为一固定的正整数,d个位移代换表π=(π1,π2,…,πd),由密钥序列K=(k1,k2,…,kd)给定,第i+td个明文字母由表πi决定。即密钥ki决定加密算法如下:ek(xi+td)=(xi+td+ki)mod(q)e_k(x_{i+td})=(x_{i+td}+k_i)mod(q)e
- 【机器学习【9】】评估算法:数据集划分与算法泛化能力评估
roman_日积跬步-终至千里
#机器学习机器学习
文章目录一、数据集划分:训练集与评估集二、K折交叉验证:提升评估可靠性1.基本原理1.1.K折交叉验证基本原理1.2.逻辑回归算法与L22.基于K折交叉验证L2算法三、弃一交叉验证(Leave-One-Out)1、基本原理2、代码实现四、ShuffleSplit交叉验证1、基本原理2、为什么能降低方差3、代码测试五、选择建议在机器学习中,评估算法的核心目标是衡量模型在“未知数据”上的表现,而不是仅
- 三轴云台之姿态调节技术篇
三轴云台的姿态调节技术通过机械解耦、传感器融合、智能控制算法及动态补偿机制协同实现,能在复杂运动环境下保持高精度稳定,其核心技术与实现方式如下:一、机械结构优化:三轴解耦与轻量化设计三轴独立驱动解耦俯仰轴(Pitch)、横滚轴(Roll)、航向轴(Yaw)通过无刷电机+编码器+驱动器模块化设计实现运动解耦,避免轴间干扰。应用场景:无人机急转弯时,航向轴优先响应姿态变化,俯仰轴同步补偿相机倾斜,横滚
- 三轴云台之电机控制技术篇
三轴云台的电机控制技术以无刷直流电机(BLDC)为核心执行单元,结合磁场定向控制(FOC)、闭环反馈、多算法融合及减震设计,实现高精度、低延迟、抗干扰的稳定姿态调整。一、电机选型:无刷直流电机(BLDC)的优势高效率与低噪音BLDC电机通过电子换向替代传统电刷,减少机械摩擦,效率可达90%以上,同时噪音降低10-15dB,满足云台对静音和续航的要求。高精度控制配合编码器(如磁编码器)可实现0.01
- 三轴云台之控制算法协同技术篇
SKYDROID云卓小助手
人工智能算法机器学习网络自动化
三轴云台的控制算法协同技术是确保云台在复杂动态环境下实现高精度、高稳定性运动控制的核心,其技术体系涵盖多传感器融合、多算法协同以及多目标优化三个关键维度。以下从技术架构与实现路径展开分析:一、多传感器融合:构建环境感知基础三轴云台通过集成IMU(惯性测量单元)、编码器、视觉传感器等多源数据,构建高鲁棒性的环境感知系统。IMU与编码器融合IMU提供高频率的姿态角速度数据,编码器提供低延迟的关节位置反
- 椭圆曲线密码学 Elliptic Curve Cryptography
AIMercs
BTC密码学密码学
密码学是研究在存在对抗行为的情况下还能安全通信的技术。即算法加密信息,再算法解密出信息。加密分为两类1.Symmetric-keyEncryption(secretkeyencryption)即一种密钥,加密和解密使用同一密钥,可相互转换2.Asymmetric-keyEncryption(publickeyencryption)分为公钥和私钥,不能转换,密钥搬运难题,用公钥加密,私钥解密椭圆密码
- 古典密码设计思想与经典算法:从罗马军团到数字世界的密码学之旅
算法第二深情
密码学密码学
一、古典密码设计思想:信息的“魔法变形术”1.核心思想古典密码学的基本目标是通过变换明文字符的位置或形式,使其对未授权者不可读。其核心设计思想分为两种:置换(Permutation):打乱字符顺序,但保留字符本身替代(Substitution):用其他字符替换原字符,改变字符内容这两种操作如同“整理书架”和“换衣服”的区别:置换:把书架上的书按新顺序排列(位置变化)替代:把每本书的内容替换成其他文
- 二分查找进阶:查找最靠左和最靠右的索引(Java实现)
算法第二深情
算法学习算法javaintellij-idea
一、引言在实际开发中,二分查找(BinarySearch)是一种高效的查找算法,尤其在处理有序数组时表现出色。然而,标准的二分查找只能返回目标值的任意一个位置(例如中间位置)。如果需要找到目标值的最左索引或最右索引(例如统计重复元素的出现次数),或者只需要单纯知道最左或最有二、普通二分查找vs.边界查找1.普通二分查找publicstaticintbinarySearch(int[]arr,int
- java Illegal overloaded getter method with ambiguous type for propert的解决
zwllxs
javajdk
好久不来iteye,今天又来看看,哈哈,今天碰到在编码时,反射中会抛出
Illegal overloaded getter method with ambiguous type for propert这么个东东,从字面意思看,是反射在获取getter时迷惑了,然后回想起java在boolean值在生成getter时,分别有is和getter,也许我们的反射对象中就有is开头的方法迷惑了jdk,
- IT人应当知道的10个行业小内幕
beijingjava
工作互联网
10. 虽然IT业的薪酬比其他很多行业要好,但有公司因此视你为其“佣人”。
尽管IT人士的薪水没有互联网泡沫之前要好,但和其他行业人士比较,IT人的薪资还算好点。在接下的几十年中,科技在商业和社会发展中所占分量会一直增加,所以我们完全有理由相信,IT专业人才的需求量也不会减少。
然而,正因为IT人士的薪水普遍较高,所以有些公司认为给了你这么多钱,就把你看成是公司的“佣人”,拥有你的支配
- java 实现自定义链表
CrazyMizzz
java数据结构
1.链表结构
链表是链式的结构
2.链表的组成
链表是由头节点,中间节点和尾节点组成
节点是由两个部分组成:
1.数据域
2.引用域
3.链表的实现
&nbs
- web项目发布到服务器后图片过一会儿消失
麦田的设计者
struts2上传图片永久保存
作为一名学习了android和j2ee的程序员,我们必须要意识到,客服端和服务器端的交互是很有必要的,比如你用eclipse写了一个web工程,并且发布到了服务器(tomcat)上,这时你在webapps目录下看到了你发布的web工程,你可以打开电脑的浏览器输入http://localhost:8080/工程/路径访问里面的资源。但是,有时你会突然的发现之前用struts2上传的图片
- CodeIgniter框架Cart类 name 不能设置中文的解决方法
IT独行者
CodeIgniterCart框架
今天试用了一下CodeIgniter的Cart类时遇到了个小问题,发现当name的值为中文时,就写入不了session。在这里特别提醒一下。 在CI手册里也有说明,如下:
$data = array(
'id' => 'sku_123ABC',
'qty' => 1,
'
- linux回收站
_wy_
linux回收站
今天一不小心在ubuntu下把一个文件移动到了回收站,我并不想删,手误了。我急忙到Nautilus下的回收站中准备恢复它,但是里面居然什么都没有。 后来我发现这是由于我删文件的地方不在HOME所在的分区,而是在另一个独立的Linux分区下,这是我专门用于开发的分区。而我删除的东东在分区根目录下的.Trash-1000/file目录下,相关的删除信息(删除时间和文件所在
- jquery回到页面顶端
知了ing
htmljquerycss
html代码:
<h1 id="anchor">页面标题</h1>
<div id="container">页面内容</div>
<p><a href="#anchor" class="topLink">回到顶端</a><
- B树、B-树、B+树、B*树
矮蛋蛋
B树
原文地址:
http://www.cnblogs.com/oldhorse/archive/2009/11/16/1604009.html
B树
即二叉搜索树:
1.所有非叶子结点至多拥有两个儿子(Left和Right);
&nb
- 数据库连接池
alafqq
数据库连接池
http://www.cnblogs.com/xdp-gacl/p/4002804.html
@Anthor:孤傲苍狼
数据库连接池
用MySQLv5版本的数据库驱动没有问题,使用MySQLv6和Oracle的数据库驱动时候报如下错误:
java.lang.ClassCastException: $Proxy0 cannot be cast to java.sql.Connec
- java泛型
百合不是茶
java泛型
泛型
在Java SE 1.5之前,没有泛型的情况的下,通过对类型Object的引用来实现参数的“任意化”,任意化的缺点就是要实行强制转换,这种强制转换可能会带来不安全的隐患
泛型的特点:消除强制转换 确保类型安全 向后兼容
简单泛型的定义:
泛型:就是在类中将其模糊化,在创建对象的时候再具体定义
class fan
- javascript闭包[两个小测试例子]
bijian1013
JavaScriptJavaScript
一.程序一
<script>
var name = "The Window";
var Object_a = {
name : "My Object",
getNameFunc : function(){
var that = this;
return function(){
- 探索JUnit4扩展:假设机制(Assumption)
bijian1013
javaAssumptionJUnit单元测试
一.假设机制(Assumption)概述 理想情况下,写测试用例的开发人员可以明确的知道所有导致他们所写的测试用例不通过的地方,但是有的时候,这些导致测试用例不通过的地方并不是很容易的被发现,可能隐藏得很深,从而导致开发人员在写测试用例时很难预测到这些因素,而且往往这些因素并不是开发人员当初设计测试用例时真正目的,
- 【Gson四】范型POJO的反序列化
bit1129
POJO
在下面这个例子中,POJO(Data类)是一个范型类,在Tests中,指定范型类为PieceData,POJO初始化完成后,通过
String str = new Gson().toJson(data);
得到范型化的POJO序列化得到的JSON串,然后将这个JSON串反序列化为POJO
import com.google.gson.Gson;
import java.
- 【Spark八十五】Spark Streaming分析结果落地到MySQL
bit1129
Stream
几点总结:
1. DStream.foreachRDD是一个Output Operation,类似于RDD的action,会触发Job的提交。DStream.foreachRDD是数据落地很常用的方法
2. 获取MySQL Connection的操作应该放在foreachRDD的参数(是一个RDD[T]=>Unit的函数类型),这样,当foreachRDD方法在每个Worker上执行时,
- NGINX + LUA实现复杂的控制
ronin47
nginx lua
安装lua_nginx_module 模块
lua_nginx_module 可以一步步的安装,也可以直接用淘宝的OpenResty
Centos和debian的安装就简单了。。
这里说下freebsd的安装:
fetch http://www.lua.org/ftp/lua-5.1.4.tar.gz
tar zxvf lua-5.1.4.tar.gz
cd lua-5.1.4
ma
- java-递归判断数组是否升序
bylijinnan
java
public class IsAccendListRecursive {
/*递归判断数组是否升序
* if a Integer array is ascending,return true
* use recursion
*/
public static void main(String[] args){
IsAccendListRecursiv
- Netty源码学习-DefaultChannelPipeline2
bylijinnan
javanetty
Netty3的API
http://docs.jboss.org/netty/3.2/api/org/jboss/netty/channel/ChannelPipeline.html
里面提到ChannelPipeline的一个“pitfall”:
如果ChannelPipeline只有一个handler(假设为handlerA)且希望用另一handler(假设为handlerB)
来
- Java工具之JPS
chinrui
java
JPS使用
熟悉Linux的朋友们都知道,Linux下有一个常用的命令叫做ps(Process Status),是用来查看Linux环境下进程信息的。同样的,在Java Virtual Machine里面也提供了类似的工具供广大Java开发人员使用,它就是jps(Java Process Status),它可以用来
- window.print分页打印
ctrain
window
function init() {
var tt = document.getElementById("tt");
var childNodes = tt.childNodes[0].childNodes;
var level = 0;
for (var i = 0; i < childNodes.length; i++) {
- 安装hadoop时 执行jps命令Error occurred during initialization of VM
daizj
jdkhadoopjps
在安装hadoop时,执行JPS出现下面错误
[slave16]
[email protected]:/tmp/hsperfdata_hdfs# jps
Error occurred during initialization of VM
java.lang.Error: Properties init: Could not determine current working
- PHP开发大型项目的一点经验
dcj3sjt126com
PHP重构
一、变量 最好是把所有的变量存储在一个数组中,这样在程序的开发中可以带来很多的方便,特别是当程序很大的时候。变量的命名就当适合自己的习惯,不管是用拼音还是英语,至少应当有一定的意义,以便适合记忆。变量的命名尽量规范化,不要与PHP中的关键字相冲突。 二、函数 PHP自带了很多函数,这给我们程序的编写带来了很多的方便。当然,在大型程序中我们往往自己要定义许多个函数,几十
- android笔记之--向网络发送GET/POST请求参数
dcj3sjt126com
android
使用GET方法发送请求
private static boolean sendGETRequest (String path,
Map<String, String> params) throws Exception{
//发送地http://192.168.100.91:8080/videoServi
- linux复习笔记 之bash shell (3) 通配符
eksliang
linux 通配符linux通配符
转载请出自出处:
http://eksliang.iteye.com/blog/2104387
在bash的操作环境中有一个非常有用的功能,那就是通配符。
下面列出一些常用的通配符,如下表所示 符号 意义 * 万用字符,代表0个到无穷个任意字符 ? 万用字符,代表一定有一个任意字符 [] 代表一定有一个在中括号内的字符。例如:[abcd]代表一定有一个字符,可能是a、b、c
- Android关于短信加密
gqdy365
android
关于Android短信加密功能,我初步了解的如下(只在Android应用层试验):
1、因为Android有短信收发接口,可以调用接口完成短信收发;
发送过程:APP(基于短信应用修改)接受用户输入号码、内容——>APP对短信内容加密——>调用短信发送方法Sm
- asp.net在网站根目录下创建文件夹
hvt
.netC#hovertreeasp.netWeb Forms
假设要在asp.net网站的根目录下建立文件夹hovertree,C#代码如下:
string m_keleyiFolderName = Server.MapPath("/hovertree");
if (Directory.Exists(m_keleyiFolderName))
{
//文件夹已经存在
return;
}
else
{
try
{
D
- 一个合格的程序员应该读过哪些书
justjavac
程序员书籍
编者按:2008年8月4日,StackOverflow 网友 Bert F 发帖提问:哪本最具影响力的书,是每个程序员都应该读的?
“如果能时光倒流,回到过去,作为一个开发人员,你可以告诉自己在职业生涯初期应该读一本, 你会选择哪本书呢?我希望这个书单列表内容丰富,可以涵盖很多东西。”
很多程序员响应,他们在推荐时也写下自己的评语。 以前就有国内网友介绍这个程序员书单,不过都是推荐数
- 单实例实践
跑龙套_az
单例
1、内部类
public class Singleton {
private static class SingletonHolder {
public static Singleton singleton = new Singleton();
}
public Singleton getRes
- PO VO BEAN 理解
q137681467
VODTOpo
PO:
全称是 persistant object持久对象 最形象的理解就是一个PO就是数据库中的一条记录。 好处是可以把一条记录作为一个对象处理,可以方便的转为其它对象。
BO:
全称是 business object:业务对象 主要作用是把业务逻辑封装为一个对象。这个对
- 战胜惰性,暗自努力
金笛子
努力
偶然看到一句很贴近生活的话:“别人都在你看不到的地方暗自努力,在你看得到的地方,他们也和你一样显得吊儿郎当,和你一样会抱怨,而只有你自己相信这些都是真的,最后也只有你一人继续不思进取。”很多句子总在不经意中就会戳中一部分人的软肋,我想我们每个人的周围总是有那么些表现得“吊儿郎当”的存在,是否你就真的相信他们如此不思进取,而开始放松了对自己的要求随波逐流呢?
我有个朋友是搞技术的,平时嘻嘻哈哈,以
- NDK/JNI二维数组多维数组传递
wenzongliang
二维数组jniNDK
多维数组和对象数组一样处理,例如二维数组里的每个元素还是一个数组 用jArray表示,直到数组变为一维的,且里面元素为基本类型,去获得一维数组指针。给大家提供个例子。已经测试通过。
Java_cn_wzl_FiveChessView_checkWin( JNIEnv* env,jobject thiz,jobjectArray qizidata)
{
jint i,j;
int s