前缀和&差分

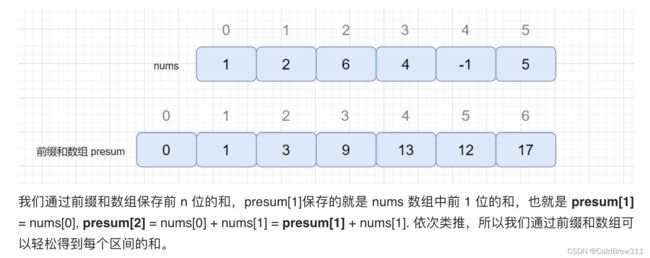
前缀和

一个只用初始化一次，但是却要反复检索计算多次，需要在最开始做预处理。

=======================以下请看版权声明

for (int i = 0; i < nums.length; i++) {
      presum[i+1] = nums[i] + presum[i];
 }

作者：chefyuan
链接：https://leetcode-cn.com/problems/continuous-subarray-sum/solution/de-liao-wo-ba-qian-zhui-he-miao-de-gan-g-c8kp/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

=======================

=======================以下请看版权声明

将matrix[][]的前缀和数组定义为prefix[][],定义prefix[i][j]表示从[0, 0]位置到[i, j]位置的子矩阵所有元素的和。

                                               S(O,D)=S(O,C)+S(O,B)−S(O,A)+D

如果求 preSum[i][j]preSum[i][j] 表示的话，对应了以下的递推公式：

       preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i][j]

根据preSum求子矩形面积：

                                         S(A,D)=S(O,D)−S(O,E)−S(O,F)+S(O,G)

如果要求 [row1, col1][row1,col1] 到 [row2, col2][row2,col2] 的子矩形的面积的话，用 preSum 对应了以下的递推公式：

preSum[row2][col2] - preSum[row2][col1 - 1] - preSum[row1 - 1][col2] + preSum[row1 - 1][col1 - 1]

===================================

作者：fuxuemingzhu
链接：https://leetcode-cn.com/problems/range-sum-query-2d-immutable/solution/ru-he-qiu-er-wei-de-qian-zhui-he-yi-ji-y-6c21/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

所以以上方法用java代码表示就是如下所示：

    private int[][] preSum;

    public NumMatrix(int[][] matrix) {
        if (matrix.length > 0) {
            preSum = new int[matrix.length + 1][matrix[0].length + 1];
            for (int i = 0; i < matrix.length; i++) {
                for (int j = 0; j < matrix[0].length; j++) {
                    preSum[i+1][j+1] = preSum[i][j+1] + preSum[i+1][j]
                                       - preSum[i][j] + matrix[i][j];
                }
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2 + 1][col2 + 1] 
               - preSum[row2 + 1][col1] - preSum[row1][col2 + 1]
               + preSum[row1][col1];
    }

leetcode304

这道题可以借鉴在matrix中选择一块小矩阵，计算其中矩阵的元素和

class NumMatrix {
    int[][] sums;
    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        if (m > 0) {
            int n = matrix[0].length;
            sums = new int[m][n + 1];
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    sums[i][j + 1] = sums[i][j] + matrix[i][j];
                }
            }
        }
    }

    /**
    * row1 col1 左上角的坐标
    * row2 col2 右下角的坐标
    **/
    public int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int i = row1; i <= row2; i++) {
            sum += sums[i][col2 + 1] - sums[i][col1];
        }
        return sum;
    }
}

如果针对一个矩阵，要找到这个矩阵中固定大小子矩阵的和，可以借鉴前缀和：

    int[][] sums;
    public int countMatrixPrefix(int[][] matrix, int cnt) {
        int m = matrix.length;
        if (m > 0) {
            int n = matrix[0].length;
            sums = new int[m][n + 1];
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    sums[i][j + 1] = sums[i][j] + matrix[i][j];
                }
            }
        }
        PriorityQueue queue = new PriorityQueue<>(Collections.reverseOrder());
        for (int i = 0; i < matrix.length - cnt + 1; i++) {
            for (int j = 0; j < matrix[0].length - cnt + 1; j++) {
                queue.add(sumRegion(i, j, i + cnt - 1, j + cnt - 1));
            }
        }
        return queue.poll();
    }

    private int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int i = row1; i <= row2; i++) {
            sum += sums[i][col2 + 1] - sums[i][col1];
        }
        return sum;
    }

前缀和

leetcode528

/**
 * 给你一个 下标从 0 开始 的正整数数组w ，其中w[i] 代表第 i 个下标的权重。
 *
 * 请你实现一个函数pickIndex，它可以随机地从范围 [0, w.length - 1] 内（含0和w.length - 1）选出并返回一个下标。
 * 选取下标i的概率为 w[i] / sum(w) 。
 *
 * 例如，对于 w = [1, 3]，挑选下标0的概率为 1 / (1 + 3)= 0.25（即，25%），
 * 而选取下标 1 的概率为 3 / (1 + 3) = 0.75（即，75%）。
 *
 * 这个题是怎么把按照权重随机取值转化成前缀和的呢？
 * 可以看到题目中选择下标的概率是该下标的权重占总权重total的多少
 * 所以题目转化成在[1, total]范围内的所有整数分成n个部分，n为权重的个数
 *      第i个部分恰好包含w[i]个整数，并且这n个部分两两无交集。
 *      然后我们在[i, total]范围内随机选择一个整数，如果整数被包含在第i个部份内，就返回i。
 * 实行以下的划分方法，按照从小到大的顺序依次划分每个部分，例如 w = [3, 1, 2, 4]时，权重和为10
 *      1.那么就将10划分为w.length个部分，每个部分分配到的数字的个数为w[i]的值，如下：
 *          [1,3],[4,4],[5,6],[7,10],此时他们的长度分别为3，1，2，4
 *      2.每个区间左边界是在它之前出现的所有元素和+1，右边界是到它为止的所有元素的和。
 *      3.如果用前缀和数组pre[i]表示w的前缀和：
 *          pre[i] = w[0] + w[1] + ... + w[i]
 *          因此第i个区间的左边界 pre[i] - w[i] + 1,右边界 pre[i]
 *      4.划分完成以后，假设随机到了整数x，那么希望查找到它存在于哪个区间内
 *          可以用二分法查找到最小的i，满足x <= pre[i]
 */

    // 前缀和数组
    int[] pre;
    // 权重和
    int total;

    public WeightRandomChoice(int[] w) {
        pre = new int[w.length];
        pre[0] = w[0];
        for (int i = 0; i < w.length; i++) {
            pre[i] = pre[i - 1] + w[i];
        }
        total = Arrays.stream(w).sum();
    }

    public int pickIndex() {
        int x = (int)(Math.random() * total) + 1;
        return binarySearch(x);
    }

    private int binarySearch(int x) {
        int low = 0;
        int high = pre.length - 1;
        while (low < high) {
            int mid = low + (high - low) / 2;
            if (pre[mid] < x) {
                low = mid + 1;
            } else {
                high = mid;
            }
        }
        return low;
    }

 

差分题

差分原理：

/**
 * 使用差分。
 * 当需要重复在一定区间内统一增量相同的值，任务是将增量叠加得到答案。
 * 差分数组的第i个数为原数组的第i - 1个元素和第i个元素的差值
 * 于是对差分数组求前缀和可以得到原数组
 *
 * 差分数组的性质：
 * 当我们希望
 * 对原数组的某个区间[left, right]施加一个增量increase时，
 * 对差分数组d对应的改变是d[left]增加increase，d[r + 1]减少increase。
 * 这时，对原数组的区间的增量修改，变成了对差分数组的两个位置的修改
 *
 * 并且这种修改是可以叠加的。
 *     当我们需要对原数组进行多次区间的修改时，我们只需要按规则修改差分数组即可
 */

leetcode1109 航班预定系统

    public int[] corpFlightBookings(int[][] bookings, int n) {
        /**
         * 本题应用差分数组的算法过程
         * 1.遍历给定的预定记录数组，完成对差分数组的修改
         * 2.完成差分数组修改后，只需要最后求出差分数组的前缀和即可得到目标数组
         * 3.本题日期从1开始，注意下标对应：
         *      对预定记录booking=[l, r, inc]要让d[l - 1]增加inc，d[r]减少inc
         *      当r = n时无需修改d[r]
         */
        int[] difference = new int[n];
        for (int[] booking : bookings) {
            difference[booking[0] - 1] += booking[2];
            if (booking[1] < n) {
                difference[booking[1]] -= booking[2];
            }
        }
        for (int i = 1; i < n; i++) {
            difference[i] += difference[i - 1];
        }
        return difference;
    }

leetcode1094. 拼车 字少的题题狠话不多

    public boolean carPooling(int[][] trips, int capacity) {
        int max = 0;
        // for循环找到最大的下车地点
        for (int[] trip : trips) {
            if (max < trip[2]) {
                max = trip[2];
            }
        }
        int[] place = new int[max + 1]; // 地点数组，i位置有place[i]人上车
        for (int[] trip : trips) {
            place[trip[1]] += trip[0];
            place[trip[2]] -= trip[0];
        }

        int count = 0; // 记录乘客数量
        for (int i = 0; i < place.length; i++) {
            count += place[i];
            if (count > capacity) {
                return false;
            }
        }
        return true;
    }