动力学约束下的运动规划算法——状态栅格规划器(State Lattice Planner)
A*、RRT等算法建立的用于路径搜索的图模型是不考虑机器人的动力学约束的,其构建的图模型的两个相邻节点之间的路径可能是不可行的,或者很难被机器人跟踪的,现在我们想要使得图中相邻两个节点间的连接是一种满足动力学约束的可行的连接,那么如何构建一个这样的图呢?
构建这样的图通常有两种方法:第一种是基于控制空间的采样(正向方法),把机器人的控制空间进行离散,然后驱动机器人往前运动,得到一个个的轨迹,如常用的DWA算法,第二种是基于状态空间的采样(逆向方法),把机器人的状态空间进行离散,产生很多的状态,然后寻找从一个状态到另一个状态的连接,如常用的TEB算法
前面介绍的A*、RRT等算法在搜索或采样构建图的时候也可看作是对状态空间的离散,现在我们建立一个描述机器人运动的状态方程 s ˙ = f ( s , u ) \dot{s}=f(s,u) s˙=f(s,u),其中s表示所有可能的状态,比如位置信息x,y、速度信息 x ˙ 、 y ˙ \color{red}{\dot{x}}、{\dot{y}} x˙、y˙等,u表示控制输入。当然我们还需要知道机器人的初始状态 s 0 s_0 s0
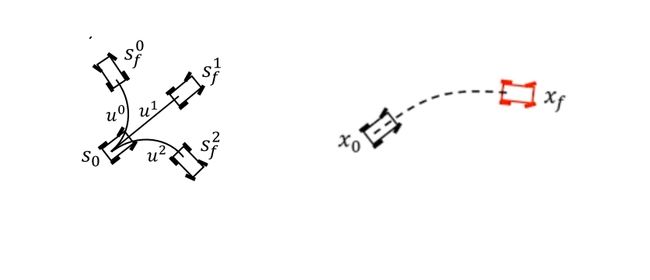
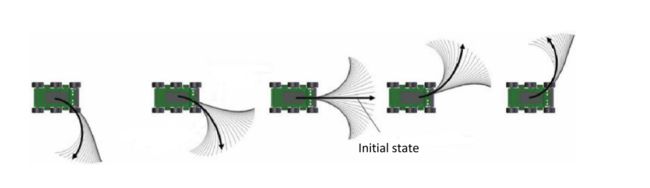
基于机器人当前的状态,当我们给予不同的输入u时,自然会产生不同运动轨迹,如下面的左图所示,这种基于控制空间的采样(正向方法)的优点是简单,易于实现,它的缺点是没有任务导向,它并不关心要前往的目标点在哪,虽然可以产生较好的规划结果,但规划效率较低。; 若已知机器人当前的状态以及目标点的状态(比如位置信息、姿态信息),如何从这两个状态解出中间的路径(边),并得到T时刻的控制量u,如下面的右图所示,这就是基于状态空间的采样(逆向方法),它的优点是有很好的任务导向,难点是难以实现。
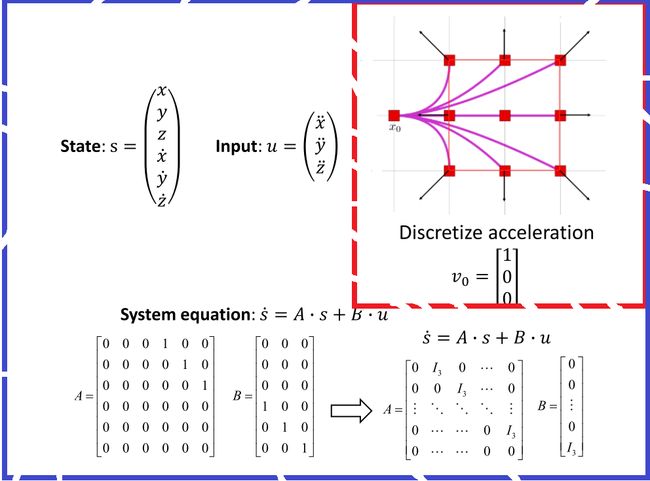
在下图的例子中,若无人机的状态选为三维位置和三维速度,输入选为三维加速度,构建状态方程 s ˙ = A ⋅ s + B ⋅ u \dot{s}=A\cdot s+B\cdot u s˙=A⋅s+B⋅u,采用不同的输入值,基于控制空间的采样得到的轨迹如下面的右图所示
–
若将状态选为三维位置、三维速度,三维加速度,输入选为三维jerk,则采用不同的输入值,基于控制空间的采样得到的轨迹如下面的右图所示:
由状态方程 s ˙ = A ⋅ s + B ⋅ u \dot{s}=A\cdot s+B\cdot u s˙=A⋅s+B⋅u,可解出具体的状态转移方程如下所示,若A是幂零矩阵,则有 A m A^m Am次方之后均为0,这样就可以通过泰勒展开的方式很容易的计算 e A t e^{At} eAt项。
有了上面的基础,接下来正式开始状态栅格规划器(State Lattice Planner)的介绍,给定一个初始的状态,给定不同的控制输入,模拟一段时间,就可以得到一系列到达不同末端位置的轨迹,若在这些不同的末端位置,再分别给定不同的控制输入,再模拟一段时间,又可以得到一系列到达不同末端位置的轨迹,依次类推,不断地向外扩展,如下图所示(左图把u分为9种,右图把u分为25种):
需要注意的是lattice graph在线构建的时候,并不需要向上图那样对所有的方向都不断地向外扩展下去,我们可以利用启发信息,优先朝目标所在的方向扩展,可以减少时间,提高效率。与提前建好的栅格地图不同,lattice graph是边搜索边构建的,即仅构建需要的节点,减少了计算时间和储存空间
下图中给出了一个基于控制空间的采样(正向方法)的示例,边采样边构建搜索树,若采样输入生成的边不与障碍物相交,则将该边添加到搜索树中
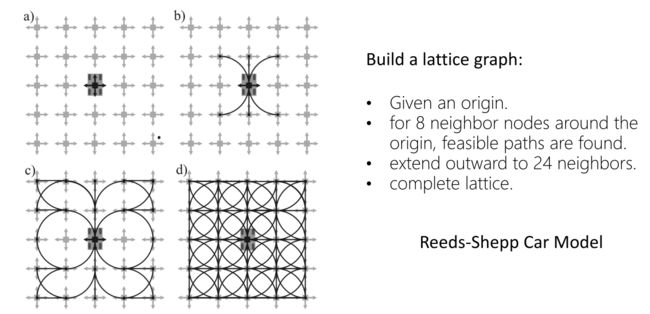
接下来,我们再来看一个基于状态空间的采样(逆向方法)的示例,假设下图中小车的模型是Reeds-Sheep模型,即小车只能基于当前状态选择向前直行、向前左转、向前右转、向后倒车、向后左转、向后右转,这6种运动形式,如下面的b图所示,这样在我们得到目标点后,可以在当前位置与目标位置之间的进行状态采样,然后再计算相邻两个状态点之间应该采用这6种运动形式中的哪一种来进行连接,最终构成到达目标点的完整路径。
下图中给出了一个只有两层的Lattice graph,先在以机器人为圆心,一定距离为半径的圆上取若干个采样点,这些采样点作为中状态,反算出机器人到这些中状态的连接方式,构成了第一层Lattice graph,然后再以机器人为圆心,更大距离为半径的圆上取若干个采样点,反算出这些采样点到中状态的连接方式,构成了第二层Lattice graph。至此,以中状态为跳板,我们可以得到从当前位置到达任何一个采样点的轨迹,得到了下图所示的两层Lattice graph的结果。
值得注意的是该两层Lattice graph中,第一层,从机器人当前位置到达中状态的轨迹是不确定的,这取决于机器人的当前状态,然而第二层,从中状态到达大圆上采样点的轨迹可以是确定的,他不受机器人当前状态的影响。
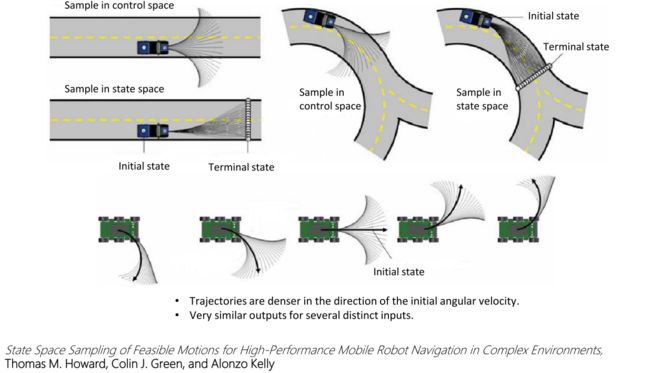
下图中给出了一些在状态空间采样和在控制空间采样的不同轨迹对比,可以看出相比于在控制空间采样,在状态空间采样的路径更优,但也存在着计算两个状态点之间轨迹不那么容易得问题。
下图中给出了在状态空间采样和在控制空间采样的示意图,对于在状态空间采样,可以离线生成Lattice图,然后在线进行搜索求解
采用单层网格规划是一种常见的局部避碰方法,如DWA算法。也可以采用轨迹库的形式,生成一系列轨迹,然后基于多项成本函数,对每个轨迹进行评级打分,选择出轨迹库中的最优轨迹。
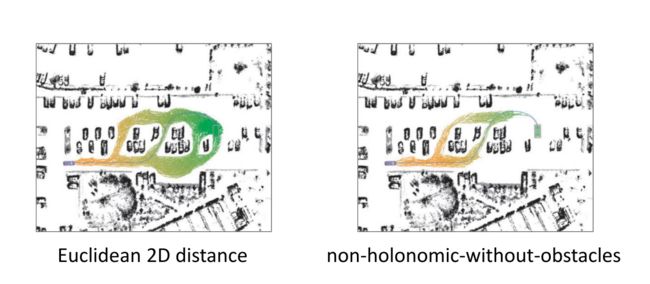
使用Lattice Planner进行规划时,也可以使用启发函数来提高规划效率,我们设计启发式函数时有两种,一种是不考虑障碍物(下面的左图),另一种是不考虑机器人的动力学模型(下面的右图),在工程上常采用两者的集合,进行叠加或者取最大值
下图中给出了使用欧氏距离作为启发函数和使用考虑动力学模型但不考虑障碍物的启发函数的效果对比:
最后,我们来看一种特殊的Lattice Planner,在无人驾驶中常使用Frenet-serret坐标系下进行规划,在道路环境中存在着车道线,我们常常希望汽车去做一个车道线的跟随,此时我们可以沿着车道线去分解设定坐标系,沿着车道线方向为s轴,其径向方向为d轴,如下图所示,依然可以采用之前的思路,对运动方程进行参数化
d ( t ) = a d 0 + a d 1 t + a d 2 t 2 + a d 3 t 3 + a d 4 t 4 + a d 5 t 5 s ( t ) = a s 0 + a s 1 t + a s 2 t 2 + a s 3 t 3 + a s 4 t 4 + a s 5 t 5 \begin{aligned}d(t)&=a_{d0}+a_{d1}t+a_{d2}t^2+a_{d3}t^3+a_{d4}t^4+a_{d5}t^5\\s(t)&=a_{s0}+a_{s1}t+a_{s2}t^2+a_{s3}t^3+a_{s4}t^4+a_{s5}t^5\end{aligned} d(t)s(t)=ad0+ad1t+ad2t2+ad3t3+ad4t4+ad5t5=as0+as1t+as2t2+as3t3+as4t4+as5t5
对于径向方向其满足当前姿态和期望的终末姿态,我们期望汽车再终末时刻在车道线上,即期望它的径向速度和加速度为0, D ( T ) = ( d f 0 0 ) D(T)=\begin{pmatrix}d_f&0&0\end{pmatrix} D(T)=(df00),然后采用OBVP的方式解最优控制问题就可以了
对于切线的方向,情况比较复杂,存在很多种情况,比如停车任务,换车道任务,速度保持,对于不同的情况一般采用不同的策略。
这里放一下zhm_real/MotionPlanning运动规划库中的Lattice Planner源码,需要注意的是该源码调用了zhm_real/MotionPlanning运动规划库中的其他程序,所有下面放的源码仅仅为了帮助理解Lattice Planner算法,想要运行的话,建议下载完整的zhm_real/MotionPlanning运动规划库,链接如下:
https://github.com/zhm-real/MotionPlanning/tree/master
import os
import sys
import math
import copy
import numpy as np
import matplotlib.pyplot as plt
sys.path.append(os.path.dirname(os.path.abspath(__file__)) +
"/../../MotionPlanning/")
from CurvesGenerator import cubic_spline, quintic_polynomial, quartic_polynomial
import LatticePlanner.env as env
import LatticePlanner.draw as draw
class C:
# Parameter
MAX_SPEED = 50.0 / 3.6
MAX_ACCEL = 8.0
MAX_CURVATURE = 2.5
ROAD_WIDTH = 8.0
ROAD_SAMPLE_STEP = 1.0
T_STEP = 0.15
MAX_T = 5.0
MIN_T = 4.0
TARGET_SPEED = 30.0 / 3.6
SPEED_SAMPLE_STEP = 5.0 / 3.6
# cost weights for Cruising
K_JERK = 0.1
K_TIME = 0.1
K_V_DIFF = 1.0
K_OFFSET = 1.5
K_COLLISION = 500
# cost weights for Stopping
# K_JERK = 0.1
# K_TIME = 0.1
# K_V_DIFF = 200
# K_OFFSET = 1.0
# K_COLLISION = 500
# parameters for vehicle
K_SIZE = 0.9
RF = 4.5 * K_SIZE # [m] distance from rear to vehicle front end of vehicle
RB = 1.0 * K_SIZE # [m] distance from rear to vehicle back end of vehicle
W = 3.0 * K_SIZE # [m] width of vehicle
WD = 0.7 * W # [m] distance between left-right wheels
WB = 3.5 * K_SIZE # [m] Wheel base
TR = 0.5 * K_SIZE # [m] Tyre radius
TW = 1 * K_SIZE # [m] Tyre width
MAX_STEER = 0.6 # [rad] maximum steering angle
class Path:
def __init__(self):
self.t = []
self.l = []
self.l_v = []
self.l_a = []
self.l_jerk = []
self.s = []
self.s_v = []
self.s_a = []
self.s_jerk = []
self.x = []
self.y = []
self.yaw = []
self.ds = []
self.curv = []
self.cost = 0.0
def sampling_paths_for_Cruising(l0, l0_v, l0_a, s0, s0_v, s0_a, ref_path):
PATHS = dict()
for s1_v in np.arange(C.TARGET_SPEED * 0.6, C.TARGET_SPEED * 1.4, C.TARGET_SPEED * 0.2):
for t1 in np.arange(4.5, 5.5, 0.2):
path_pre = Path()
path_lon = quartic_polynomial.QuarticPolynomial(s0, s0_v, s0_a, s1_v, 0.0, t1)
path_pre.t = list(np.arange(0.0, t1, C.T_STEP))
path_pre.s = [path_lon.calc_xt(t) for t in path_pre.t]
path_pre.s_v = [path_lon.calc_dxt(t) for t in path_pre.t]
path_pre.s_a = [path_lon.calc_ddxt(t) for t in path_pre.t]
path_pre.s_jerk = [path_lon.calc_dddxt(t) for t in path_pre.t]
for l1 in np.arange(-C.ROAD_WIDTH, C.ROAD_WIDTH, C.ROAD_SAMPLE_STEP):
path = copy.deepcopy(path_pre)
path_lat = quintic_polynomial.QuinticPolynomial(l0, l0_v, l0_a, l1, 0.0, 0.0, t1)
path.l = [path_lat.calc_xt(t) for t in path_pre.t]
path.l_v = [path_lat.calc_dxt(t) for t in path_pre.t]
path.l_a = [path_lat.calc_ddxt(t) for t in path_pre.t]
path.l_jerk = [path_lat.calc_dddxt(t) for t in path_pre.t]
path.x, path.y = SL_2_XY(path.s, path.l, ref_path)
path.yaw, path.curv, path.ds = calc_yaw_curv(path.x, path.y)
l_jerk_sum = sum(np.abs(path.l_jerk))
s_jerk_sum = sum(np.abs(path.s_jerk))
v_diff = abs(C.TARGET_SPEED - path.s_v[-1])
path.cost = C.K_JERK * (l_jerk_sum + s_jerk_sum) + \
C.K_V_DIFF * v_diff + \
C.K_TIME * t1 * 2 + \
C.K_OFFSET * abs(path.l[-1]) + \
C.K_COLLISION * is_path_collision(path)
PATHS[path] = path.cost
return PATHS
def sampling_paths_for_Stopping(l0, l0_v, l0_a, s0, s0_v, s0_a, ref_path):
PATHS = dict()
for s1_v in [-1.0, 0.0, 1.0, 2.0]:
for t1 in np.arange(1.0, 16.0, 1.0):
path_pre = Path()
path_lon = quintic_polynomial.QuinticPolynomial(s0, s0_v, s0_a, 55.0, s1_v, 0.0, t1)
path_pre.t = list(np.arange(0.0, t1, C.T_STEP))
path_pre.s = [path_lon.calc_xt(t) for t in path_pre.t]
path_pre.s_v = [path_lon.calc_dxt(t) for t in path_pre.t]
path_pre.s_a = [path_lon.calc_ddxt(t) for t in path_pre.t]
path_pre.s_jerk = [path_lon.calc_dddxt(t) for t in path_pre.t]
for l1 in [0.0]:
path = copy.deepcopy(path_pre)
path_lat = quintic_polynomial.QuinticPolynomial(l0, l0_v, l0_a, l1, 0.0, 0.0, t1)
path.l = [path_lat.calc_xt(t) for t in path_pre.t]
path.l_v = [path_lat.calc_dxt(t) for t in path_pre.t]
path.l_a = [path_lat.calc_ddxt(t) for t in path_pre.t]
path.l_jerk = [path_lat.calc_dddxt(t) for t in path_pre.t]
path.x, path.y = SL_2_XY(path.s, path.l, ref_path)
path.yaw, path.curv, path.ds = calc_yaw_curv(path.x, path.y)
if path.yaw is None:
continue
l_jerk_sum = sum(np.abs(path.l_jerk))
s_jerk_sum = sum(np.abs(path.s_jerk))
v_diff = (path.s_v[-1]) ** 2
path.cost = C.K_JERK * (l_jerk_sum + s_jerk_sum) + \
C.K_V_DIFF * v_diff + \
C.K_TIME * t1 * 2 + \
C.K_OFFSET * abs(path.l[-1]) + \
50.0 * sum(np.abs(path.s_v))
PATHS[path] = path.cost
return PATHS
def SL_2_XY(s_set, l_set, ref_path):
pathx, pathy = [], []
for i in range(len(s_set)):
x_ref, y_ref = ref_path.calc_position(s_set[i])
if x_ref is None:
break
yaw = ref_path.calc_yaw(s_set[i])
x = x_ref + l_set[i] * math.cos(yaw + math.pi / 2.0)
y = y_ref + l_set[i] * math.sin(yaw + math.pi / 2.0)
pathx.append(x)
pathy.append(y)
return pathx, pathy
def calc_yaw_curv(x, y):
yaw, curv, ds = [], [], []
for i in range(len(x) - 1):
dx = x[i + 1] - x[i]
dy = y[i + 1] - y[i]
ds.append(math.hypot(dx, dy))
yaw.append(math.atan2(dy, dx))
if len(yaw) == 0:
return None, None, None
yaw.append(yaw[-1])
ds.append(ds[-1])
for i in range(len(yaw) - 1):
curv.append((yaw[i + 1] - yaw[i]) / ds[i])
return yaw, curv, ds
def is_path_collision(path):
index = range(0, len(path.x), 5)
x = [path.x[i] for i in index]
y = [path.y[i] for i in index]
yaw = [path.yaw[i] for i in index]
for ix, iy, iyaw in zip(x, y, yaw):
d = 1.8
dl = (C.RF - C.RB) / 2.0
r = math.hypot((C.RF + C.RB) / 2.0, C.W / 2.0) + d
cx = ix + dl * math.cos(iyaw)
cy = iy + dl * math.sin(iyaw)
for i in range(len(C.obs)):
xo = C.obs[i][0] - cx
yo = C.obs[i][1] - cy
dx = xo * math.cos(iyaw) + yo * math.sin(iyaw)
dy = -xo * math.sin(iyaw) + yo * math.cos(iyaw)
if abs(dx) < r and abs(dy) < C.W / 2 + d:
return 1.0
return 0.0
def verify_path(path):
# if any([v > C.speed_max for v in path.s_v]) or \
# any([abs(a) > C.acceleration_max for a in path.s_a]):
# return False
if any([v > C.MAX_SPEED for v in path.s_v]) or \
any([abs(a) > C.MAX_ACCEL for a in path.s_a]) or \
any([abs(curv) > C.MAX_CURVATURE for curv in path.curv]):
return False
return True
def extract_optimal_path(paths):
if len(paths) == 0:
return None
while len(paths) > 1:
path = min(paths, key=paths.get)
paths.pop(path)
if verify_path(path) is False:
continue
else:
return path
return paths[-1]
def lattice_planner_for_Cruising(l0, l0_v, l0_a, s0, s0_v, s0_a, ref_path):
paths = sampling_paths_for_Cruising(l0, l0_v, l0_a, s0, s0_v, s0_a, ref_path)
path = extract_optimal_path(paths)
return path
def lattice_planner_for_Stopping(l0, l0_v, l0_a, s0, s0_v, s0_a, ref_path):
paths = sampling_paths_for_Stopping(l0, l0_v, l0_a, s0, s0_v, s0_a, ref_path)
path = extract_optimal_path(paths)
return path
def get_reference_line(x, y):
index = range(0, len(x), 3)
x = [x[i] for i in index]
y = [y[i] for i in index]
cubicspline = cubic_spline.Spline2D(x, y)
s = np.arange(0, cubicspline.s[-1], 0.1)
rx, ry, ryaw, rk = [], [], [], []
for i_s in s:
ix, iy = cubicspline.calc_position(i_s)
rx.append(ix)
ry.append(iy)
ryaw.append(cubicspline.calc_yaw(i_s))
rk.append(cubicspline.calc_curvature(i_s))
return rx, ry, ryaw, rk, cubicspline
def pi_2_pi(theta):
if theta > math.pi:
return theta - 2.0 * math.pi
if theta < -math.pi:
return theta + 2.0 * math.pi
return theta
def main_Crusing():
ENV = env.ENVCrusing()
wx, wy = ENV.ref_line
bx1, by1 = ENV.bound_in
bx2, by2 = ENV.bound_out
C.obs = np.array([[50, 10], [96, 25], [70, 40],
[40, 50], [25, 75]])
obs_x = [x for x, y in C.obs]
obs_y = [y for x, y in C.obs]
rx, ry, ryaw, rk, ref_path = get_reference_line(wx, wy)
l0 = 2.0 # current lateral position [m]
l0_v = 0.0 # current lateral speed [m/s]
l0_a = 0.0 # current lateral acceleration [m/s]
s0 = 0.0 # current course position
s0_v = 20.0 / 3.6 # current speed [m/s]
s0_a = 0.0
while True:
path = lattice_planner_for_Cruising(l0, l0_v, l0_a, s0, s0_v, s0_a, ref_path)
if path is None:
print("No feasible path found!!")
break
l0 = path.l[1]
l0_v = path.l_v[1]
l0_a = path.l_a[1]
s0 = path.s[1]
s0_v = path.s_v[1]
s0_a = path.s_a[1]
if np.hypot(path.x[1] - rx[-1], path.y[1] - ry[-1]) <= 2.0:
print("Goal")
break
dy = (path.yaw[2] - path.yaw[1]) / path.ds[1]
steer = pi_2_pi(math.atan(-C.WB * dy))
plt.cla()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
plt.plot(rx, ry, linestyle='--', color='gray')
plt.plot(bx1, by1, linewidth=1.5, color='k')
plt.plot(bx2, by2, linewidth=1.5, color='k')
plt.plot(path.x[1:], path.y[1:], linewidth='2', color='royalblue')
plt.plot(obs_x, obs_y, 'ok')
draw.draw_car(path.x[1], path.y[1], path.yaw[1], steer, C)
plt.title("[Crusing Mode] v :" + str(s0_v * 3.6)[0:4] + " km/h")
plt.axis("equal")
plt.pause(0.0001)
plt.pause(0.0001)
plt.show()
def main_Stopping():
ENV = env.ENVStopping()
wx, wy = ENV.ref_line
bx1, by1 = ENV.bound_up
bx2, by2 = ENV.bound_down
C.ROAD_WIDTH = ENV.road_width
rx, ry, ryaw, rk, ref_path = get_reference_line(wx, wy)
l0 = 0.0 # current lateral position [m]
l0_v = 0.0 # current lateral speed [m/s]
l0_a = 0.0 # current lateral acceleration [m/s]
s0 = 0.0 # current course position
s0_v = 30.0 / 3.6 # current speed [m/s]
s0_a = 0.0
while True:
path = lattice_planner_for_Stopping(l0, l0_v, l0_a, s0, s0_v, s0_a, ref_path)
if path is None:
print("No feasible path found!!")
break
l0 = path.l[1]
l0_v = path.l_v[1]
l0_a = path.l_a[1]
s0 = path.s[1]
s0_v = path.s_v[1]
s0_a = path.s_a[1]
if np.hypot(path.x[1] - 56.0, path.y[1] - 0) <= 1.5:
print("Goal")
break
plt.cla()
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
plt.plot(rx, ry, linestyle='--', color='gray')
plt.plot(bx1, by1, linewidth=1.5, color='k')
plt.plot(bx2, by2, linewidth=1.5, color='k')
plt.plot(path.x[1:], path.y[1:], linewidth='2', color='royalblue')
draw.draw_car(path.x[1], path.y[1], path.yaw[1], 0.0, C)
plt.title("[Stopping Mode] v :" + str(s0_v * 3.6)[0:4] + " km/h")
plt.axis("equal")
plt.pause(0.0001)
plt.pause(0.0001)
plt.show()
plt.plot(rx, ry, linestyle='--', color='gray')
plt.plot(bx1, by1, linewidth=1.5, color='k')
plt.plot(bx2, by2, linewidth=1.5, color='k')
plt.axis("equal")
plt.show()
if __name__ == '__main__':
main_Crusing()
# main_Stopping()
运行效果如下所示:
MotionPlanning中lattice测试
参考资料:
1、深蓝学院-移动机器人运动规划
2、zhm_real/MotionPlanning运动规划库
3、State Lattice Planner(状态栅格规划)