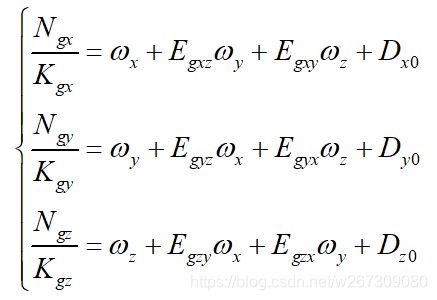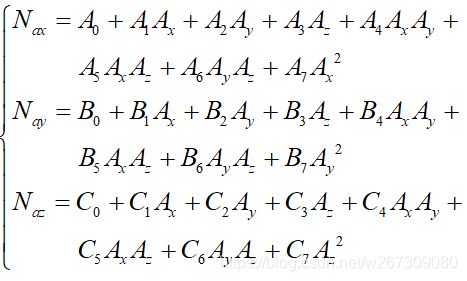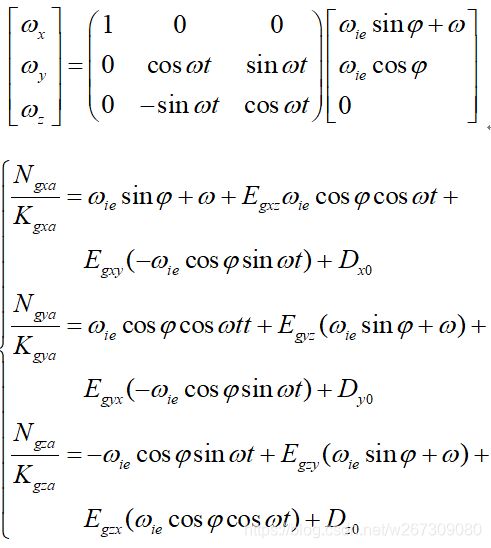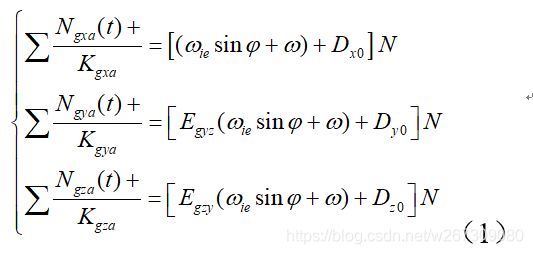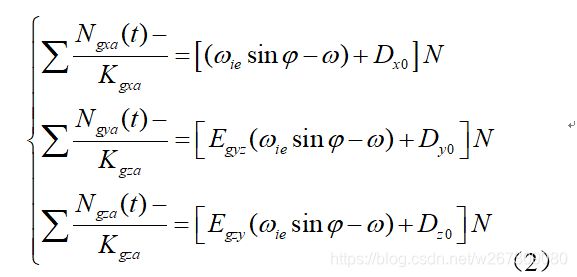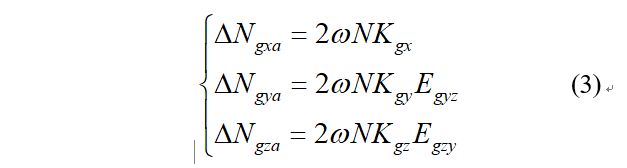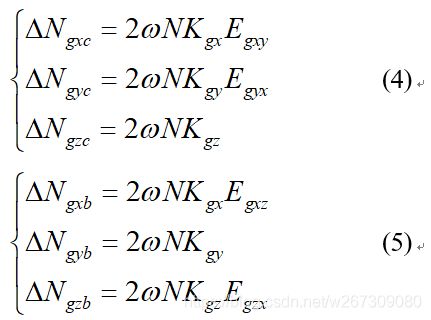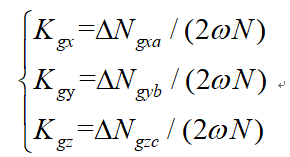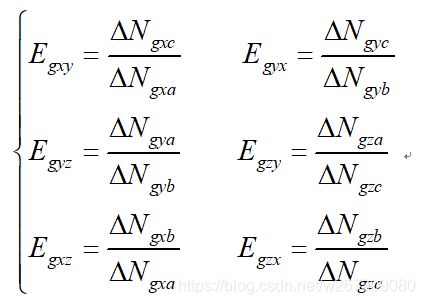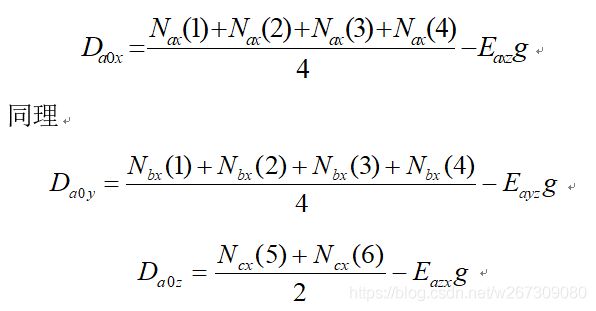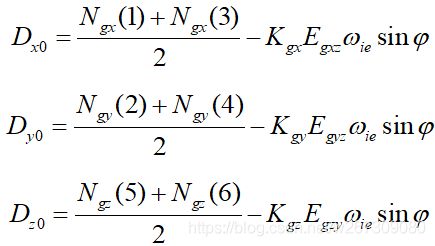船用光纤捷联系统标定技术研究
船用光纤捷联系统标定技术研究
摘 要：针对DHGL-11型光纤捷联系统的机械编排结构进行了误差模型分析、模型建立、标定试验设计、模型精度验证等，最终获得符合系统精度的系统误差模型。根据惯性器件的原理、系统精度指标和辅助设备性能等因素确定了系统的误差模型。根据误差模型，以光纤陀螺指天正、反转方案设计了速率试验；根据石英挠性加速度计的误差模型，设计了指北二十四位置的标定编排结构；并设计了零位修修证试验修证了误差模型中的零位误差。最后，设计了5 min静基座对准试验、10 min模仿船舶摇摆的动基座对准试验和4 h的模拟船舶摇摆环境的导航试验，对误差模型的标定精度进行了验证。实际证明，该标定方案可以满足DHGL-11型光纤捷联系统精度要求。
关键词：标定；光纤捷联惯性导航系统；石英加速度计；光纤陀螺
目前我国大多数船舶使用的航向导航系统都是电罗经，但电罗经在高机动时航向误差较大，不能提供姿态角信息，存在维护成本较高、寿命短等问题。光纤捷联惯导系统是电罗经的理想替代品，它不仅可以弥补电罗经的不足，而且可以提供精度更高的航姿信息，同时光纤捷联系统成本较其他同等精度的系统低。提高船用光纤捷联系统精度使其满足船舶需求的方法较多，而误差补偿是比较有效的途径。所谓误差补偿即标定试验，就是根据相关理论建立惯性仪表器件和惯性系统的模型方程，并利用专门的测试设备和有序的测试步骤，标定、计算出仪表和系统的各种误差项，进而根据观测量来对惯性仪表的输出进行补偿，从而提高仪表系统的实际使用精度[1]。
1 光纤捷联惯性系统误差模型
理论上，系统误差模型的阶数越多、项数越多，该误差模型描述的越接近真实，从而后续补偿效果越明显、越好[2]。但是，惯性元件的最终精度是与其工艺密切相关的，标定试验得到的误差模型只是在此基础上建立的。而当我们所选用误差模型的精度优于其性能指标规定的误差范围时，该模型精度优于器件精度指标的部分是没有意义的[3]。综合考虑惯性器件精度、实际操作可行性、误差模型计算难度及补偿的最终效果，应在不影响系统整体性能的前提下，折中建立器件、系统误差模型。系统模型是由器件模型组成，只是较器件模型多了安装误差项。由于器件模型相对简单，在此不单独讨论独立器件模型，器件模型将间接地体现在系统模型中。由于光学陀螺在理论上不受力学影响（或影响较小、不影响本文所涉及系统精度）[3]，所以光纤陀螺和石英加速度计的误差模型可以认为是相互独立的关系[4]。
三轴光纤陀螺仪的一般误差模型为：
石英加速度计误差模型与光纤陀螺误差模型类似，如下式。
对误差模型而言，能正确地反应出惯性仪表器件的性能、指标，又不会有太过复杂的计算过程，所以，考虑到加表二次耦合项误差较其他误差少一个数量级，故可以忽略该项误差[5]。
2 标定试验设计
标定试验就是通过试验设备给惯性系统一定激励激发出误差量，并通过多组不同位置(运动状态)的激励和惯性器件的输出组成方程组，求得误差参数。一般通过速率试验获得光纤陀螺部分误差参数；通过位置试验获得加速度计误差参数；最后通过零位修证试验来修证二者的零位误差参数。
2.1 速率试验
通过速率试验可以获得光纤捷联系统的光纤陀螺的标度因数、安装误差角和零位误差。但由于这里获得零位误差为拟合零位并不是真实零位，所以只取标度因数和安装误差角等12项误差参数。
由于光纤陀螺标度因数存在非线性，所以原则上应进行多个速率点的速率试验来获得最优的线性度。但是，采用多个速率点测试显得过于复杂、繁琐，不利于光纤捷联系统批产标定。所以选择一个合适的测试速率点显得尤其重要。通过光纤陀螺非线性度测试试验得知光纤陀螺在线性度好于其他速率区间，又由于所用转台速率精度在以内较高、较稳定。综合考虑采用较适宜。另外，由于在水平面上存在地球自转角速度的分量，且分量大小随转台外框转动周期变化，其一周均值为零。所以通过整数圈测量来消除该项影响。
控制转台分别使光纤捷联系统的坐标轴X、Y、Z指天，然后外框分别以角速度w正、反向转动，来实现速率试验。以绕X轴旋转为例，X轴角速率输出值为:
转台旋转N整周，含有误差耦合项的分量相互抵消，对N周的输出值求和得：
同理，反向旋转一周可得：
由式(1)，(2)得出
绕Y、Z轴同理：
根据式(3)~(5)得到3个光纤陀螺的标度因数为
安装误差角为
2.2 位置试验
加速度计误差参数一般通过位置试验获得[6]。加速度计位置试验法通常包括六、八、二十四、四十八位置法等[7]。考虑到加速度计的非线性度较好，四十八位置较二十四位置精度提高不大及标定时间等因素，本试验采用二十四位置法进行位置试验。通过位置试验我以确定石英加速度计的标度因数、零位误差、安装误差、二次耦合项等误差[8]以及光纤陀螺的部分误差参数。但是由于每个位置的停留时间较短（通常为1 min）及光纤陀螺的噪声较大，所以位置试验所得到的陀螺误差参数并不准确。具体标定试验步骤如下：
1）光纤捷联系统安装在三轴转台上，调节安装使3个加速度计敏感轴与转台的内、中、外框轴平行。
2)将光纤捷联系统X轴水平指向北向。控制转台使光纤捷联系统绕指北轴连续转动7次，总共8个位置（从0°以45°增量开始转动，共8个位置）；记录下各加速度计的输出值。
3)控制转台使Y、Z轴指北重复步骤2)。
这样以X轴为例，并根据X轴的24个位置对应的重力场敏感到X轴加速度计的输出值带入加速度计误差模型，可以得到24个方程，并组成方程组：
2.3 零位修证试验
零位试验的基本原理可归结为：加速度计敏感轴处在水平位置时敏感不到重力加速度，其输出量中除了安装误差引起的重力投影，其他误差和零偏均认为是零位误差。可以通过取不同的水平位置的加速度计的输出平均值对零位误差进行补偿[9]。光纤陀螺零位试验原理相同，光纤陀螺仪敏感轴在东、西方向敏感不到地球自传角速度，这时光纤陀螺的输出量中除了安装误差引起的分量都可以认为是零位误差。故通过东、西方向的光纤陀螺仪的输出平均值就可以对零位误差进行补偿[10]。
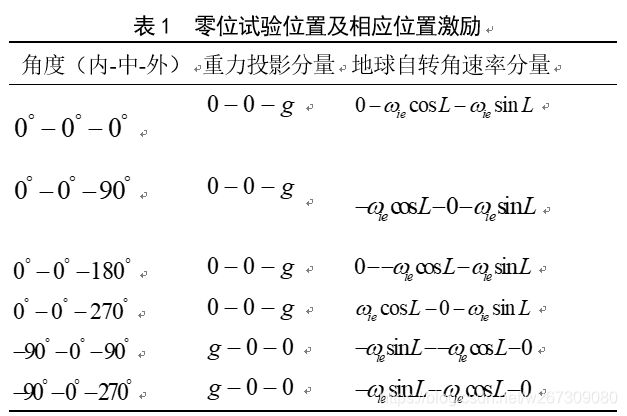
设置以下六位置零位修正试验，如表1所示。
由表1可知，在前4个位置中，X、Y加速度计均没有敏感到重力加速度，此时加速度计的输出可表示为
在东西方向上并没有地球自转角速率分量，故光纤陀螺仪此时的输出为Y、Z轴上的安装误差在X轴上的分量与零位误差之和。与加速度计类似，其表达式如下：
3 光纤捷联系统标定精度验证测试
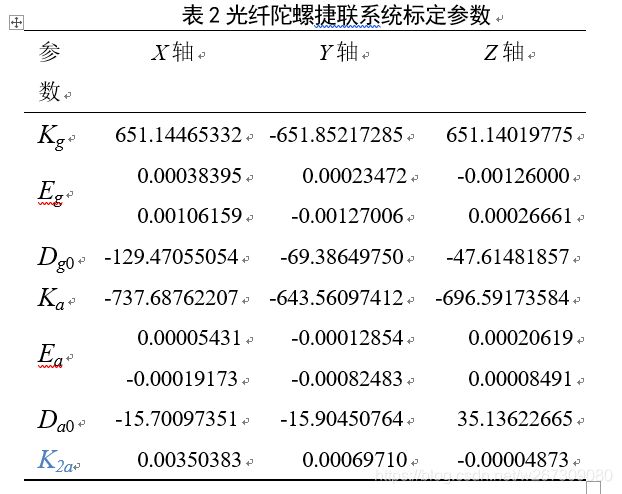
现以试验室任意一套DHGL-11型船用光纤捷联惯导系统作为被标定设备，并按照上述标定试验设计步骤在三轴转台上进行标定试验数据采集，如图1所示。最后根据误差模型编写标定计算程序，计算出系统误差模型参数。通过计算获得光纤捷联系统误差模型参数如表2所示。其中Kg、Ka分别为3个陀螺、3个加速度计的标度因数；Eg为3个陀螺间的表征安装误差项；Ea为3个加速度计间的表征安装误差项；Dg0、Da0分别为3个陀螺、3个加速度计的零位误差项；K2a为加速度计的二次非线性误差项。
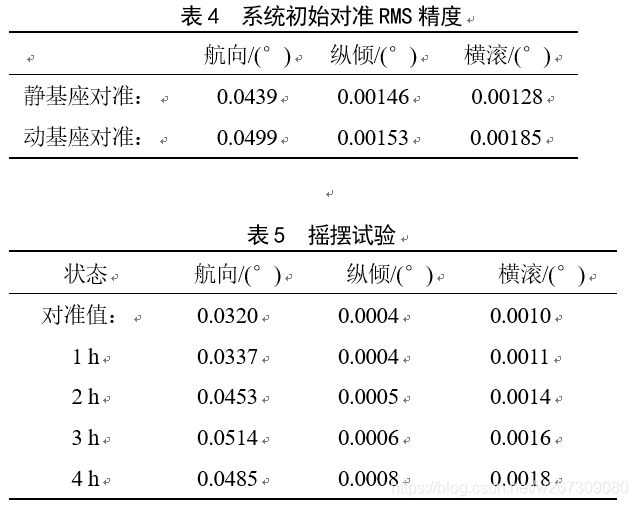
经过标定试验获得了光纤捷联系统误差模型。现通过静基座对准、动基座对准、摇摆试验来验证该表定方案的标定精度。以上试验均为无外界信息的纯惯导状态。将系统安装于转台上，调整安装误差后，分别在航向为0°、45°、90°、135°、180°、225°、270°、315°、水平状态，做静态对准试验，对准时间5 min。在0°、90°、180°、270°这4个方向上做动基座对准试验，对准时间10 min，转台内、中、外框摇摆幅值分别为20°、8°、10°，频率分别为0.2、0.2、0.125 Hz。对准试验结果如表3、表4所示。航向RMS精度小于0.05°。由精度为0.01°/h的陀螺组成的光纤捷联系统理论精度约为0.06°[9]。通过实验可知本方案标定过的光纤捷联系统误差模型精度并未降低其对准精度，且对准结果符合理论值。
对准仅是惯导系统获得初始状态值，后续还要工作在导航状态，为载体提供航姿信息、速度、位置等信息。所以还要做导航试验，来进一步验证误差模型的精度。现设计摇摆试验，系统安装在转台上，初始方向为北、姿态水平。系统静态对准5 min后记录数据，转台进入摇摆状态，摇摆参数同动基座对准，每摇1 h停止回到北向水平并记录数据，重复4次。试验结果如表5所示。这一结果验证了误差模型中的安装误差参数的准确性[10]。
通过对准、导航试验对系统误差模型精度进行了验证，说明该标定方案得到的系统误差模型不会给理论航向精度为0.06°、姿态精度为0.01°的光纤捷联系统带来引起系统超标的误差，因而设计的误差模型精度满足该精度的光纤捷联系统需求。从初始对准测试结果中可知系统航向RMS精度约为0.05°，姿态RMS精度小于0.02°，经过该方案标定的系统初始对准精度足以使得该精度级光纤捷联惯导系统初始对准精度达到最优。在摇摆试验中，四次的记录值与系统初始值变化较小，航向变化小于0.02°，姿态角变化小于0.001°，说明该标定方案所计算出的安装误差、标度因数较接近真值。通过以上验证试验，可以证明该标定方案适用于该精度级的船用光纤捷联系统需求，充分的优化了系统初始对准、导航精度。
4 结束语
通过对DHGL-11型船用光纤捷联系统的误差模型分析、建立了一套合适、快捷的标定方案。通过速率试验得到陀螺标度因数、安装误差、零位等参数；通过二十四位置试验获得加速度计标度因数、安装误差、二次非线性系数以及零位等参数；最后通过零位试验修证了零位误差参数，提高了误差模型精度。通过初始对准试验、摇摆试验测得了DHGL-11系统的对准精度和导航精度，且精度完全与理论精度吻合。这一结果证明了这种标定方案所得到的误差模型可以使得该精度级惯导系统精度达到最优。本方案较传统标定方案，在不影响精度的前提下简化了标定流程、大大的缩减了标定时间，提高了DHGL-11产品的生产效率。在摇摆试验中，随着时间的积累航姿角有发散趋势，表明该标定方案在安装误差系数修证及标度因数非线性度补偿方面略有不足，这将是今后进一步深入研究的问题。
参考文献:
- 黄德鸣, 程禄. 惯性导航系统[M]. 哈尔滨: 哈尔滨工程大学出版社, 1999: 1-2.
- 严恭敏, 李四海, 秦永元. 惯性仪器测试与数据分析[M]. 北京: 国防工业出版社, 2012: 1-21,143-179.
- 严恭敏, 秦永元. 激光捷联惯组的双轴位置转台标定仿真[J]. 中国惯性技术学报, 2007, 15(1): 123-127.
- 刘保良, 邓玉芬, 张博. 利用Allan方差进行光纤陀螺测试[J]. 现代电子技术, 2012, 13: 126-127.
- 蒋效雄, 刘雨, 苏宝库. 高精度加速度计重力场标定试验方法[J]. 吉林大学学报: 工学版, 2010(1): 287-292.
- 高钟毓. 惯性导航系统初始对准与标定最优化方法[J]. 中国惯性技术学报, 2009(1): 1-7.
- 查峰, 高敬东, 许江宁, 等. 光学陀螺捷联惯性系统的发展与展望[J]. 激光与光电子学进展, 2011(7): 1-6.
- 胡鑫, 韩崇伟, 李伟, 等.基于四位置转位法实现激光捷联惯性测量组合标定[J]. 科学技术与工程, 2010(8): 2034-2037.
- 罗超. FOG捷联惯性导航系统标定和误差补偿技术[D]. 哈尔滨: 哈尔滨工程大学, 2006: 11-24.
- 司宏源, 庞秀枝, 鲁浩. 捷联惯性导航装置全温度标定方法[J]. 光电与控制, 2007, 14(6): 127-130,143.