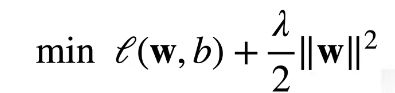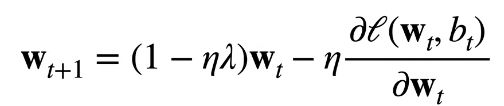动手学深度学习（四）多层感知机

目录

一、多层感知机的从零开始实现

1.1 初始化模型参数

1.2 实现Relu函数

1.3 实现模型

1.4 训练

二、多层感知机的简洁实现

2.1 实现模型

2.2 训练

三、模型选择

3.1 训练误差和泛化误差

3.2 验证数据集和测试数据集

3.3 过拟合和欠拟合

3.4 代码实现

3.4.1 生成训练和测试数据的标签

3.4.2 评估损失

3.4.3 训练函数

3.4.4 正常拟合（使用三阶多项式函数的数据特征）

3.4.5 欠拟合（使用线性函数的数据特征）

3.4.6 过拟合（使用高阶多项式函数的数据特征）

四、权重衰减

4.1 范数与权重衰减

4.2  代码实现

4.2.1 生成数据

4.2.2 初始化模型参数

4.2.3 定义L2范数惩罚 (核心)

4.2.4 训练函数

4.2.5 训练

4.2.6 简洁实现

五、数值稳定性和模型初始化

---

经过了多层感知机后，相当于将原始的特征转化成了新的特征，或者说提炼出更合适的特征，这就是隐藏层的作用。

from：清晰理解多层感知机和反向传播 - 知乎

一、多层感知机的从零开始实现

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256 # 批量大小
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) # 读取数据集

1.1 初始化模型参数

实现一个具有隐藏层的多层感知机，它包含256个隐藏单元。

# 初始化模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256     # 输入特征数量，输出类别，隐藏单元

W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)  # 第一层的权重矩阵
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))  # 第一层的偏置向量

W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01) # 第二层的权重矩阵
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))  # 第二层的偏置向量
params = [W1, b1, W2, b2]   # nn.Parameter为需要优化的张量分配地址空间

nn.Parameter()是PyTorch中用于定义可训练参数的类。在神经网络模型中，我们可以通过定义nn.Parameter()来创建需要优化的可训练的张量。

1.2 实现Relu函数

# 实现Relu激活函数
def relu(X):
    a = torch.zeros_like(X)
    return  torch.max(X, a)

1.3 实现模型

# 实现模型
def net(X):
    X = X.reshape((-1, num_inputs)) # 将图像拉伸为长度为num_inputs的向量
    H = relu(X @ W1 + b1) # @为矩阵乘法，输出为长度为num_hiddens的向量，传入下一层
    return (H @ W2 + b2)

loss = nn.CrossEntropyLoss() # 交叉熵损失

1.4 训练

# 训练
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr) # 定义优化算法
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

二、多层感知机的简洁实现

引用API更简洁实现多层感知机。

import torch
from torch import nn
from d2l import torch as d2l

2.1 实现模型

# 实现模型
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 10)) # 隐藏层有256个单元

def init_weights(m):    # 初始化参数
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

2.2 训练

# 训练
batch_size, lr, num_epochs = 256, 0.1, 10

loss = nn.CrossEntropyLoss(reduction='none') # 交叉熵损失
trainer = torch.optim.SGD(net.parameters(), lr=lr) # 优化算法
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) # 传入数据

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

三、模型选择

3.1 训练误差和泛化误差

训练误差：模型在训练数据上的误差。

泛化误差（测试误差）：模型在新数据上的误差。（我们着重关心的）

例子︰根据摸考成绩来预测未来考试分数。

在过去的考试中表现很好(训练误差)不代表未来的考试一定会好(泛化误差)。

3.2 验证数据集和测试数据集

验证数据集：验证数据集(Validation Datasets)是训练模型时所保留的数据样本,我们在调整模型超参数时,需要根据它来对模型的能力进行评估。（一个用来评估模型好坏的数据集）

测试数据集：测试数据集(Test Datasets)是一个在建模阶段没有使用过的数据集。一旦根据验证数据集确定了“最好”的模型,那么在测试集上对模型的性能评估。（只用一次的数据集）

Q：为什么要设立验证数据集？

A：如果我们在模型选择的过程中使用测试数据，可能会有过拟合测试数据的风险。

K折交叉验证：在没有足够的多数据时使用（这是常态）

算法：

•     将训练数据分割成K块
•     For i = 1,2,…,K
•         使用第 i 块作为验证数据集，其余的作为训练数据集
•     报告K个验证集误差的平均

常用：K=5或10。

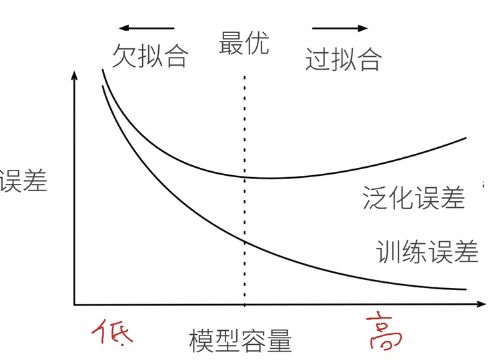
3.3 过拟合和欠拟合

过拟合：训练误差明显小于验证误差。（这不一定是坏事，深度学习领域预测模型在训练集上的表现往往在验证集上的表现好得多）

欠拟合：训练误差和验证误差之间的差距很小，而且误差值都很大，需要寻找更复杂的模型来减小训练误差。

1. 模型容量（模型复杂性）

• 拟合各种函数的能力
• 低容量的模型难以拟合训练数据
• 高容量的模型可以记住所有的训练数据

（一般取泛化误差最小的模型容量为最优）

2. 比较模型容量

难以在不同种类算法之间比较。

•     例如树模型和神经网络

给定一个模型种类，有两个主要因素：

•     参数的个数
•     参数值的选择范围

3. 数据的复杂度

因素：

• 样本个数
• 每个样本的元素个数
• 时间、空间结构
• 多样性（多少类的分类）

3.4 代码实现

import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l

max_degree = 20  # 多项式的最大阶数
n_train, n_test = 100, 100  # 训练数据和测试数据的大小
true_w = np.zeros(max_degree)  # 初始化权重参数w，均为0
true_w[:4] = np.array([5, 1.2, -3.4, 5.6])  # 参数w前四个的取值，用作充当真实值

3.4.1 生成训练和测试数据的标签

使用以下三阶多项式来生成训练和测试数据的标签：

# 生成训练和测试数据的标签
features = np.random.normal(size=(n_train + n_test, 1))  # 随机正态分布生成数据集样本
np.random.shuffle(features)  # 打乱数据集
poly_features = np.power(features,
                         np.arange(max_degree).reshape(1, -1))  # 按列表下标依次求1到20次幂
for i in range(max_degree):
    poly_features[:, i] /= math.gamma(i + 1)  # gamma(n)=(n-1)!


labels = np.dot(poly_features, true_w)  # 作点积运算，求结果y
labels += np.random.normal(scale=0.1, size=labels.shape)  # 随机正态分布生成偏置项

# numpy ndarray转换为tensor
true_w, features, poly_features, labels = [torch.tensor(x, dtype=
    torch.float32) for x in [true_w, features, poly_features, labels]]

3.4.2 评估损失

def evaluate_loss(net, data_iter, loss):
    """评估给定数据集上模型的损失"""
    metric = d2l.Accumulator(2)  # 累加器，存放模型总损失、样本总数
    for X, y in data_iter:
        out = net(X)
        y = y.reshape(out.shape)
        l = loss(out, y)
        metric.add(l.sum(), l.numel())  # 将损失值总和和样本总数添加入累加器

    return metric[0] / metric[1]  # 返回平均损失

3.4.3 训练函数

# 训练函数
def train(train_features, test_features, train_labels, test_labels, num_epochs=400):
    loss = nn.MSELoss(reduction='none')             # 平方误差损失函数
    input_shape = train_features.shape[-1]

    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))  # 线性层

    batch_size = min(10, train_labels.shape[0])  

    train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),
                                batch_size)
    test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),
                               batch_size, is_train=False)

    trainer = torch.optim.SGD(net.parameters(), lr=0.01)    #小批量随机梯度下降优化算法
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
                            xlim=[1, num_epochs], ylim=[1e-3, 1e2],
                            legend=['train', 'test'])

    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
                                     evaluate_loss(net, test_iter, loss)))

    print('weight:', net[0].weight.data.numpy())

3.4.4 正常拟合（使用三阶多项式函数的数据特征）

我们将首先使用三阶多项式函数，它与数据生成函数的阶数相同。 结果表明，该模型能有效降低训练损失和测试损失。 学习到的模型参数也接近真实值w=[5,1.2,−3.4,5.6] 。

# 训练
# 拟合(正常)，给足训练特征和验证特征
train(poly_features[:n_train, :4], poly_features[n_train:,:4],  # 多项式特征[200,20]，前4列中，前100行划为训练集，后100行划为验证集
     labels[:n_train], labels[n_train:])

weight: [[ 5.0149393  1.2182785 -3.4234915  5.535555 ]]，已学习到的模型参数也接近真实值w=[5, 1.2, -3.4, 5.6]。

poly_features，为多项式特征矩阵，大小为[200,20]，列数为多项式的阶数。

3.4.5 欠拟合（使用线性函数的数据特征）

 线性函数的数据训练三阶多项式模型，模型过于复杂，数据多样性不够或过少导致欠拟合。

# 欠拟合，训练特征和验证特征减半
train(poly_features[:n_train, :2], poly_features[n_train:,:2],
     labels[:n_train], labels[n_train:])

3.4.6 过拟合（使用高阶多项式函数的数据特征）

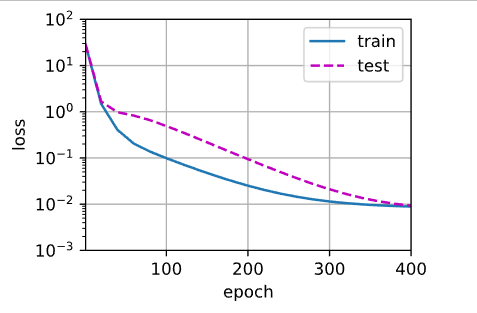
高阶多项式的数据训练三阶多项式模型，数据特征过于复杂（或过多），模型不足以支撑，导致数据中的噪声一并学习到，使得到最后产生了过拟合，训练损失可以有效地降低，但测试损失仍然很高。

# 过拟合，从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:,:],
     labels[:n_train], labels[n_train:], num_epochs=1500)

四、权重衰减

“范数”参考：动手学深度学习（一）预备知识_向岸看的博客-CSDN博客

Q：为什么要引入惩罚项？

A：为防止模型过拟合，提高模型的泛化能力，通常会在损失函数的后面添加一个正则化项。
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓惩罚是指对损失函数中的某些参数做一些约束，使得参数的自由度变小。

Q：正则化在深度学习中含义是指什么?

A：正则化其实是一种策略，以增大训练误差为代价来减少测试误差的所有策略我们都可以称作为正则化。换句话说就是正则化是为了防止模型过拟合。L2范数就是最常用的正则化方法之一。

4.1 范数与权重衰减

权重衰退通过L2正则项使得模型参数不会过大，从而控制模型复杂度 。

使用均方范数作为硬性限制。通过限制参数值 的选择范围来控制模型的复杂度。

对每个 ，都可以找到 使得之前的目标函数等价于下面，实际上这是最小预测损失和惩罚项之和：

超参数 控制了正则项的重要程度，

增加了惩罚项（L2范数）后，计算梯度的公式：

更新参数的公式：

通常 ，在深度学习中通常叫做权重衰退。

Q：为什么叫做权重衰退？

A：可见公式中，，每次更新权重之前，先将权重缩小一次。权重衰退通过L2正则项使得模型参数不会过大，从而控制模型复杂度。正则项权重是控制模型复杂度的超参数。

4.2  代码实现

"""导入相关库"""
import torch
from d2l import torch as d2l
from torch import nn

4.2.1 生成数据

""" 生成数据集 """
n_train, n_test, num_inputs, batch_size = 50, 100, 200, 5   # 训练集，验证集，输入变量，以及batch的大小
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.1    # 定义参数，偏置项
train_data = d2l.synthetic_data(true_w, true_b, n_train)    # 生成数据
test_data = d2l.synthetic_data(true_w, true_b, n_test)
train_iter = d2l.load_array(train_data, batch_size)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

4.2.2 初始化模型参数

""" 初始化模型参数 """
def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)  #从标准正态分布中随机选取
    b = torch.zeros(1, requires_grad=True)  # 偏置初始值为0
    return [w, b]

4.2.3 定义L2范数惩罚 (核心)

""" 定义L2范数惩罚 """
def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2

4.2.4 训练函数

""" 训练函数 """
def train(lambd):
    w, b = init_params()    #初始化参数
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
    num_epochs, lr = 100, 0.003
    # 绘图
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        # 绘制训练误差和测试误差
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())

lambda [arg1 [,arg2,.....argn]]:expression

• args：函数将接收的参数。
• expression：结果为函数返回值的表达式。

冒号前是参数，可以有多个，用逗号隔开，冒号右边的为表达式（只能为一个）。其实lambda返回值是一个函数的地址，也就是函数对象。

示例：

def sum(x,y):
    return x+y
    print(sum(1,2))
    # 使用lambda函数:
    sum = lambda x,y:x+y
    # 没有了函数sum的定义，又称为匿名函数
    print(sum(1,2)) 

4.2.5 训练

先用lambd=0，禁用权重衰退。

""" 训练 """
train(lambd=0)

从上图结果来看，存在严重的过拟合问题，验证误差远大于训练误差。

之后，我们令lambd=5，观察使用权重衰退的效果。

# 使用权重衰退
train(lambd=5)

验证误差有明显的下降。

4.2.6 简洁实现

我们在实例化优化器时直接通过weight_decay指定权重衰退超参数，注意偏置项b没有weight_decay，指定了也不会衰退。

trainer = torch.optim.SGD([
     {"params":net[0].weight,'weight_decay': wd},
     {"params":net[0].bias}], lr=lr)

五、数值稳定性和模型初始化

梯度值的乘积：

• 梯度爆炸：是指当训练深度神经网络时，梯度的值会快速增大，造成参数的更新变得过大，导致模型不稳定，难以训练。
• 梯度消失：是指当训练深度神经网络时，梯度的值会快速减小，导致参数的更新变得很小，甚至无法更新，使得模型难以学习有用的特征。

梯度爆炸的原因：

• 值超出值域(infinity)，对于16位浮点数尤为严重（数值区间6e-5 - 6e4)。
• 对学习率敏感。如果学习率太大->大参数值-→更大的梯度·如果学习率太小->训练无进展（我们可能需要在训练过程不断调整学习率）。

梯度消失的原因：

• sigmoid函数是导致梯度消失的一个常见原因。

由sigmoid的导数可见，当输入值很大或很小时，它的梯度很有可能会等于0，这样就会导致梯度消失。