统计学极简入门——区间估计

4. 区间估计

还以为你被上节课的内容唬住了~终于等到你，还好没放弃！

本节我们将说明两个问题：总体均值 $\mu$ 的区间估计和总体比例 $\bar{p}$ 的区间估计。

区间估计经常用于质量控制领域来检测生产过程是否正常运行或者在“控制之中” ，也可以用来监控互联网领域各类数据指标是否在正常区间。

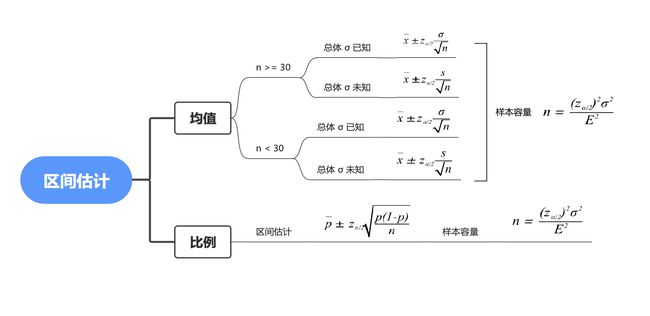
一个总体均值的区间估计

• 大样本的情况下

  • $\sigma$已知，$\bar{x}\pm z_{\alpha /2}\frac{\sigma }{\sqrt{n}}$

  • $\sigma$未知，$\bar{x}\pm z_{\alpha /2}\frac{s}{\sqrt{n}}$

• 小样本的情况下

  • $\sigma$已知，$\bar{x}\pm z_{\alpha /2}\frac{\sigma }{\sqrt{n}}$
  • $\sigma$未知，$\bar{x}\pm t_{\alpha /2}\frac{s}{\sqrt{n}}$

另外补充一个公式，样本量 $ n = \frac{({z_{\alpha/2})^2 {\sigma}^2}}{E2}$ 这个了解就好，大部分情况下是不缺数据的，尽可能选数据量稍大些的数据。

把以上过程编写成Python的自定义函数：

import numpy as np
import scipy.stats
from scipy import stats as sts


def mean_interval(mean=None, sigma=None,std=None,n=None,confidence_coef=0.95):
    """
    mean:样本均值
    sigma: 总体标准差
    std: 样本标准差
    n:   样本量
    confidence_coefficient：置信系数
    confidence_level:置信水平 置信度
    alpha:显著性水平
    功能：构建总体均值的置信区间
    """
    alpha = 1 - confidence_coef
    z_score = scipy.stats.norm.isf(alpha / 2)            # z分布临界值
    t_score = scipy.stats.t.isf(alpha / 2, df = (n-1) )  # t分布临界值
   
    if n >= 30: 
        if sigma != None:
            me = z_score * sigma / np.sqrt(n)
            print("大样本，总体 sigma 已知：z_score:",z_score)
        elif sigma == None:
            me = z_score * std / np.sqrt(n)
            print("大样本，总体 sigma 未知 z_score",z_score)
        lower_limit = mean - me
        upper_limit = mean + me
    if n < 30 :
        if sigma != None:
            me = z_score * sigma / np.sqrt(n)
            print("小样本，总体 sigma 已知 z_score * sigma / np.sqrt(n) \n z_score = ",z_score)
        elif sigma == None:
            me = t_score * std / np.sqrt(n)
            print("小样本，总体 sigma 未知 t_score * std / np.sqrt(n) \n t_score = ",t_score)
            
        print("t_score:",t_score)
        lower_limit = mean - me
        upper_limit = mean + me
    
    return (round(lower_limit, 1), round(upper_limit, 1))

应用：网站流量UV区间估计:

某网站流量UV数据如下[52,44,55,44,45,59,50,54,62,46,54,42,60,62,43,42,48,55,57,56]，我们研究一下该网站的总体流量uv均值：

先把数据放进来

import numpy as np
data = np.array([52,44,55,44,45,59,50,54,62,46,54,42,60,62,43,42,48,55,57,56])

计算一下均值为：

x_bar = data.mean()
x_bar
# 51.5

样本标准差为：

x_std = sts.tstd(data,ddof = 1) #  ddof=1时,分母为n-1;ddof=0时,分母为n
x_std
# 6.840283158189472

mean_interval(mean=x_bar, sigma=None,std= x_std,  n=n, confidence_coef=0.95)

输出结果：

小样本，总体 sigma 未知 t_score * std / np.sqrt(n) 
t_score =  2.093024054408263
(48.3, 54.7)

于是我们有95%的把握，该网站的流量uv介于 [48, 55]之间。

值得一提的是，上面这个案例的数据是实际上是公众号山有木兮水有鱼 的按天统计阅读量……有人可能要说了，你这数据也太惨了，而且举个案例都是小样本。我想说，小样本的原因是这新号一共发了也没几天，至于数量低，你帮忙动动小手转发转发，这数据也就高了~希望下次举例的时候这个能变成大样本，均值怎么着也得个千儿八百的，感谢感谢！

一个总体比例的区间估计

$\bar{p}\pm z_{\alpha /2}\sqrt{\frac{\bar{p}(1-\bar{p})}{n}}$

其中样本量 $n=\frac{(z_{\alpha /2}{)}^2{p}^{\ast }(1-p^{\ast })}{E^2}$

def proportion_interval(p=None, n=None, confidence_coef =0.95):
    """
    p: 样本比例
    n: 样本量
    confidence_coef: 置信系数
    功能：构建总体比例的置信区间
    """
    alpha = 1 - confidence_coef
    z_score = scipy.stats.norm.isf(alpha / 2)  # z分布临界值
    
    me = z_score * np.sqrt((p * (1 - p)) / n) 
    lower_limit = p - me
    upper_limit = p + me
    
    return (round(lower_limit, 3), round(upper_limit, 3))

下期将为大家带来《Python统计学极简入门》之假设检验

点击下方链接，观看下期内容。
https://edu.cda.cn/goods/show/3386