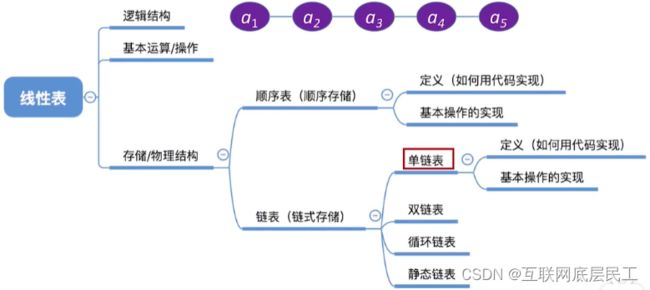
数据结构——线性表
一、线性表的类型定义
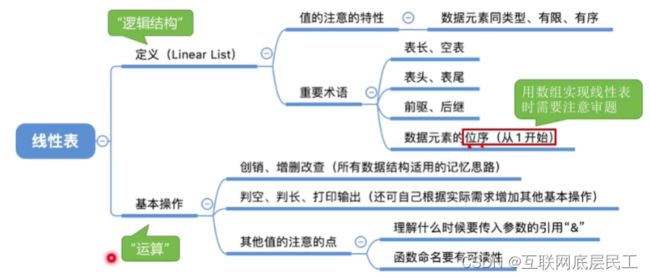
(一)基本概念:
线性表是最常见且最简单的一种数据结构。是具有相同数据类型的n(n>=0)个数据元素的有限序列,其中n为表长,当n=0时线性表是一个空表。若用L命名线性表,则其一般表示为:
L = ( a 1 , a 2 , . . . , a i , a i + 1 , . . . a n ) L = (a_1,a_2,...,a_i,a_{i+1},...a_n) L=(a1,a2,...,ai,ai+1,...an)
- ai是线性表中的“第i个”元素线性表中的位序.(注意:位序从1开始数组下标从0开始)
- a1是表头元素;an是表尾元素。
- 除第一个元素外,每个元素有且仅有一个直接前驱;除最后一个元素外,每个元素有且仅有一个直接后驱。
(二)线性表的基本操作
InitList(&L):初始化表。构造一个空的线性表L,分配内存空间。
DestroyList(&L):销毁操作。销毁线性表,并释放线性表L所占用的内存空间。
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。
ListDelete(&L,i,&e):删除操作。删除表L中第i个位置的元素,并用e返回删除元素的值。
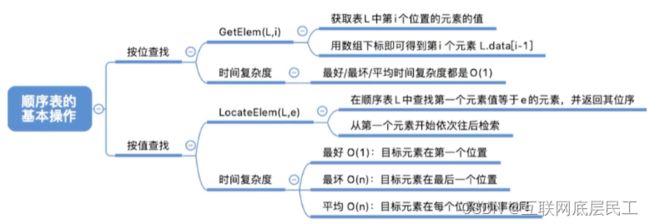
GetElem(L,i):按位查找操作。获取表L中第i个位置的元素的值。
LocateElem(L,e):按值查找操作。在表L中查找具有给定关键字值的元素。
ClearList(&L):将L重置为空表。
其他常用操作:
Length(L):求表长。返回L中数据元素个数。
PrintList(L):输出操作。按前后顺序输出线性表L的所有元素值。
Empty(L):判空操作。若L位空表,则返回true,否则返回false。
线性表L的初始化(参数用引用)
Status InitList_Sq(SqList &L){ //构造一个空的顺序表L
L.elem=new ElemType[MAXSIZE]; //为顺序表分配空间
if(!L.elem) exit(OVERFLOW); //存储分配失败
L.length=0; //空表长度为0
return OK;
}
销毁线性表L
void DestroyList(SqList &L){
if(L.elem) delete l.elelm; //释放存储空间
}
清空线性表L
void ClearList(SqList &L){
L.length=0; //将线性表的长度置为0
}
求线性表L的长度
int GetLength(SqList L){
return(L.length);
}
判断线性表L是否为空
int IsEmpty(SqList L){
if(L.length==0) return 1;
else return 0;
}
二、线性表的顺序表示和实现
(一)定义
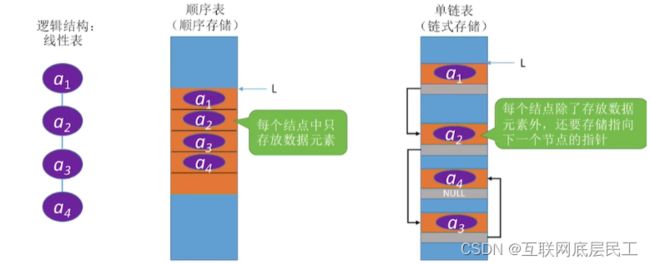
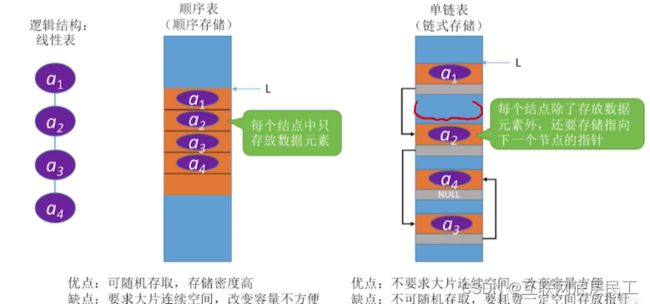
线性表的顺序表示又称为顺序存储结构或顺序映像。
顺序表:用顺序存储的方式实现线性表。
顺序存储:把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系由存储单元的邻接关系来体现。
顺序存储方法:用一组地址连续的存储单元依次存储线性表的元素。
假设线性表的每个元素需占用l个存储单元,并以所占的第一个单元的存储地址作为数据元素的存储位置。则线性表中第i+1个数据元素的存储位置LOC(a{i+1}) 和第个数据元素的存储位置LOC(ai)之间满足下列关系:
L O C ( a i + 1 ) = L O C ( a i ) + l LOC(a_{i+1}) = LOC(a_i)+l LOC(ai+1)=LOC(ai)+l
一般来说,线性表的第i个数据元素ai的存储位置为:
L O C ( a i ) = L O C ( a 1 ) + ( i − 1 ) ∗ l LOC(a_i) = LOC(a_1) + (i-1)*l LOC(ai)=LOC(a1)+(i−1)∗l
以元素在计算机内的“物理位置相邻”来表示线性表中数据元素之间的逻辑关系。每一个数据元素的存储位置都和线性表的起始位置相差一个和数据元素在线性表中的位序成正比的常数。
顺序表的特点
1、随机访问,可以在O(1)时间内找到第i个元素
2、存储密度高,每个节点只存储数据元素
3、扩展容量不方便
4、插入、删除操作不方便,需要移动大量元素
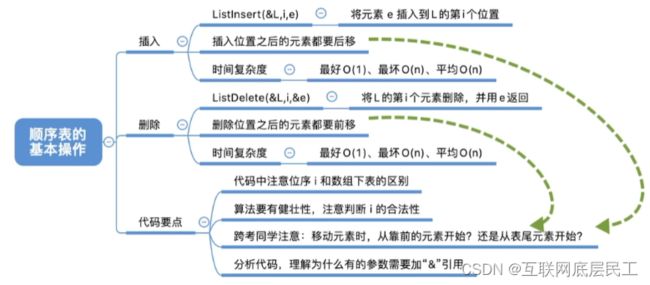
(二)顺序表的基本操作
数据结构的基本运算:修改、插入、删除、查找、排序
1、修改
通过数组的下标便可访问某个特定元素并修改之。
核心语句:V[i] = x;
2、插入
在线性表的第i个位置前插入一个元素
(1)实现步骤
- 将第n至第i位的元素向后移动一个位置
- 将要插入的元素写到第i个位置
- 表长加1
注意:事先应判断插入位置i是否合法?表是否已满?
应当符合条件: 1<=i<=n+1 或 i=[1,n=1]
(2)核心语句
for(j=n;j>=i;j--)
a[j+1]=a[j]; //元素后移一个位置
a[i]=x; //插入x
n++; //表长加1
(3)代码实现:
#define MaxSize 10 //定义最大长度
typedef struct{
Elemtype data[MaxSize]; //用静态的“数组”存放数据元素
int length; //顺序表的当前长度
}SqList //顺序表的类型定义
void ListInsert(SqList &L,int i,int e){
for(int j=L.Length;j>=i;j--)//将第i个元素及之后的元素后移
L.data[j]=L.data[j-1];
L.data[i-1]=e; //在位置i除放入e
L.length++; //长度加1
}
int main() {
SqList L; //声明一个顺序表
InitList(L); //初始化顺序表
//...此处省略一些代码,插入几个元素
ListInsert(L, 3, 3);
return 0;
}
(4)插入操作的时间复杂度
bool ListInsert(SqList &L,int i,int e){
if(i<1||i>L.length+1) //判断i的范围是否有效
return false;
if(L.length>=MaxSize) //当前存储空间已满,不能插入
return false;
for(int j=L.length;j>=i;j--)//将第i个元素及之后的元素后移
L.data[j]=L.data[j-1];
L.data[i-1]=e; //在位置i处放入e
L.length++; //长度加1
return ture;
}
最好情况:新元素插入到表尾,不需要移动元素。
i=n+1,循环0次;最好时间复杂度 = O(1)
最坏情况:新元素插入到表头,需要将原有的n个元素全都向后移动
i=1,循环n次;最坏时间复杂度 = O(n);
平均情况:假设新元素插入到任何一个位置的概率相同,即i = 1,2,3…,length+1的概率都是p=1/(n+1)。
i=1,循环n次;i=2时,循环n-1次;i=3,循环 n-2次 … i=n+1时,循环0次。
平均循环次数:
n p + ( n − 1 ) p + ( n − 2 ) p + . . . + 1 ∗ p = n ( n + 1 ) 2 = 1 n + 1 = n 2 np+(n-1)p+(n-2)p+...+1*p=\frac{n(n+1)}{2}=\frac{1}{n+1}=\frac{n}{2} np+(n−1)p+(n−2)p+...+1∗p=2n(n+1)=n+11=2n
平均时间复杂度=O(n)
3、删除
删除线性表的第i个位置上的元素
(1)实现步骤:
- 将第i+1至第n位的元素向前移动一个位置
- 表长减一
注意:实现需要判断,删除位置i是否合法?
应符合条件:1<=i<=n 或 i = [1,n]
(2)核心语句:
for(j=i+1;j<=n;j++)
a[j-1]=a[j]; //元素前移一个位置
n--;
(3)代码实现
bool ListDelete(SqList &L,int i,int &e){
if(i<1||i>L.length) //判断i的范围是否有效
return false;
e=L.data[i-1]; //将被删除的元素赋值给e
for(int j=i;j<L.length;j++) //将第i个位置后的元素前移
L.data[j-1]=L.data[j];
L.length--; //线性表长度减1
return true;
}
int main(){
SqList L; //声明一个顺序表
InitList(L); //初始化顺序表
//...此处省略一些代码,插入几个元素
int e = -1; //用变量e把删除的元素“带回来
if(ListDelete(L, 3, e))
printf("已删除第3个元素,删除元素值为=%d\n",e);
else
printf("位序i不合法,删除失败\n");
return 0;
}
(4)删除操作的时间复杂度
bool ListDelete(SqList &L,int i,int &e){
if(i<1||i>L.length) //判断i的范围是否有效
return false;
e=L.data[i-1]; //将被删除的元素赋值给e
for(int j=i;j<L.length;j++) //将第i个位置后的元素前移
L.data[j-1]=L.data[j];
L.length--; //线性表长度减1
return true;
}
最好情况:删除表尾元素,不需要移动其他元素。
i=n,循环0次;最好时间复杂度 = O(1)
最坏情况:删除表头元素,需要将原有的n-1个元素全都向前移动
i=1,循环n-1次;最坏时间复杂度 = O(n);
平均情况:假设删除任何一个元素的概率相同,即i = 1,2,3…,length+1的概率都是p=1/n。
i=1,循环n-1次;i=2时,循环n-2次;i=3,循环 n-3次 … i=n时,循环0次。
平均循环次数:
( n − 1 ) p + ( n − 2 ) p + . . . + 1 ∗ p = n ( n − 1 ) 2 ∗ 1 n = n − 1 2 (n-1)p+(n-2)p+...+1*p=\frac{n(n-1)}{2}*\frac{1}{n}=\frac{n-1}{2} (n−1)p+(n−2)p+...+1∗p=2n(n−1)∗n1=2n−1
平均时间复杂度=O(n)
4、查找
(1)按位查找
GetElem(L,i):按位查找操作。获取表L中第 i 个位置的元素的值。
静态分配
#define MaxSize 10 //定义最大长度
typedef struct{
Elemtype data[MaxSize]; //用静态的“数组”存放数据元素
int length; //顺序表的当前长度
}SqList //顺序表的类型定义
ElemType GetElem(SqList L,int i){
return L.data[i-1];
}
动态分配
#define InitSize 10 //顺序表的初始化长度
typedef struct{
ElemType *data; //指示动态分配数组的指针
int MaxSize; //顺序表的最大容量
int length; //顺序表的当前长度
}SeqList //顺序表类型定义(动态分配方式)
ElemType GetElem(SeqList L, int i){
return L.data[i-1];
}
时间复杂度:O(1)
由于顺序表的各个数据元素在内存中连续存放,因此可以根据起始地址和数据元素大小立即找到第 i 个元素——“随机存取”特性
(2)按值查找
LocateElem(L,e):按值查找操作。在表L中查找具有给定关键字值的元素。
#define InitSize 10 //顺序表的初始化长度
typedef struct{
ElemType *data; //指示动态分配数组的指针
int MaxSize; //顺序表的最大容量
int length; //顺序表的当前长度
}SeqList //顺序表类型定义(动态分配方式)
//在顺序表L中查找第一个元素值等于e的元素,并返回其位序
int LocateElem(SeqList L,ElemType e){
for(int i=0;i<L.length;i++){
if(L.data[i]==e)
return i+1; //数组下标为i的元素等于e,返回其位序i+1
return 0; //退出循环,说明查找失败
}
}
注意:在c语言中,结构体的比较不能直接使用“==”
时间复杂度:
最好情况:目标元素在表头。
循环1次;最好时间复杂度 = O(1)
最坏情况:目标元素在表尾
循环n次;最坏时间复杂度 = O(n);
平均情况:假设目标元素出现在任何一个位置的概率相同,都是1/n
目标元素在第1位,循环1次;在第二位,循环2次;…;在第n位,循环n次。
平均循环次数 :
1 ∗ 1 n + 2 ∗ 1 n + 3 ∗ 1 n + . . . + n ∗ 1 n = n ( n + 1 ) 2 ∗ 1 n = n + 1 2 1*\frac{1}{n}+2*\frac{1}{n}+3*\frac{1}{n}+...+n*\frac{1}{n}=\frac{n(n+1)}{2}*\frac{1}{n}=\frac{n+1}{2} 1∗n1+2∗n1+3∗n1+...+n∗n1=2n(n+1)∗n1=2n+1
所以平均时间复杂度 = O(n)
(三)顺序表的运算效率分析
1、时间效率分析
算法时间主要耗费在移动元素的操作上,因此计算时间复杂度的基本操作(最深层语句频度)
T ( n ) = o ( 移动元素次数 ) T(n) = o(移动元素次数) T(n)=o(移动元素次数)
而移动元素的个数取决于插入或删除元素的位置。
2、空间效率分析
顺序表插入、删除算法的平均控件复杂度为:
T ( n ) = o ( 1 ) T(n) = o(1) T(n)=o(1)
因为没有占用辅助空间。
(四)元素类型说明(补充)
1、顺序表类型定义
typedef struct{
ElemType data[];
int length;
}SqList; //顺序表类型
ElemType代表数据类型,编写代码时使用具体类型(例如:插入,int等)替换ElemType位置。或在代码中提前定义:
typedef char ElemType;
typedef int ElemType;
当数据元素是一个复杂类型时,可以定义一个结构类型:
typedef struct{
float p;
int e;
}Polynomial;
typedef struct{
Polynomial *elem;
int length;
}SqList;
2、数组定义
数组静态分配
typedef struct{
ElemType data[MaxSize];
int length;
}SqList //顺序表类型
数组动态分配
typedef struct{
ElemType *data;
int length;
}SqList //顺序表类型
分配动态数组内存
SqList L;
L.data = (ElemType*)malloc(sizeof(ElemType)*MaxSize);
3、C语言的内存动态分配
SqList L;
L.data = (ElemType*)malloc(sizeof(ElemType)*MaxSize);
- malloc(m)函数:开辟m字节长度的地址空间,并返回这段空间的首地址。
- sizeof(x)运算:计算变量x的长度
- free§函数:释放指针p所指变量的存储空间,即彻底删除一个变量。
需要加载头文件:
4、C++的动态存储分配
new 类型名T (初值列表)
int *p1 = new int;
或
int *p1 = new int(10);
功能:申请用于存放T类型对象的内存空间,并依初值列表赋以初值
结果值:
成功:T类型的指针,指向新分配的内存
失败:0(NULL)
delete 指针P
功能:释放指针P所指向的内存。P必须是new操作的返回值。
5、C++中的参数传递
- 函数调用时传送形参表的实参必须与形参三个一致(类型、个数、顺序)
- 参数传递有两种方式
- 传值方式(参数为整型、实型、字符型等)
- 传地址
- 参数为指针变量
- 参数为引用类型
- 参数为数组名
(1)传值方式
- 把实参的值传送给函数局部工作区相应的副本中,函数使用这个副本执行必要的功能。函数修改的是副本的值,实参的值不变。
#include (2)传地址方式——指针变量作参数
- 形参变化影响实参
#include - 形参变化不影响实参
#include (3)传地址方式——数组名作参数
- 传递的是数组的首地址
- 对形参数组所做的任何改变都将反映到实参数组中
#include(4)传地址方式——引用类型作参数
引用:用来给一个对象提供一个替代的名字
#includej 是一个引用类型,代表 i 的一个替代名i值改变时,j 值也跟着改变,所以会输出:i=7 j=7
#include 说明:
- 传递引用给函数与传递指针的效果是一样的,形参变化是实参也发生变化。
- 引用类型作形参,在内存中并没有产生实参的副本,它直接对实参操作;而一般变量作参数,形参与实参就占用不同的存储单元,所以形参变量的值是实参变量的副本。因此,当参数传递的数据量较大时,用引用比用一般变量传递参数的时间和空间效率都好。
- 指针参数虽然也能达到与使用引用的效果,但在被调用函数中需要重复使用“*指针变量名”的形式进行运算,这很容易产生错误且程序的阅读性较差;另一方面,在主调函数的调用点处,必须用变量的地址作为实参。
三、线性表的链式标识和实现
(一)单链表
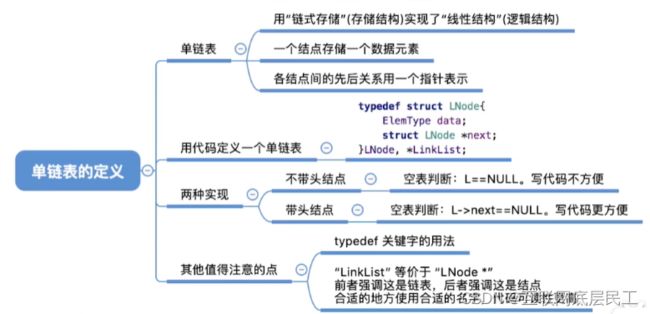
1、定义
定义:用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以是不连续的)。
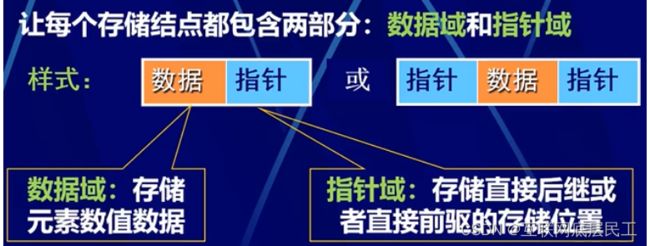
数据域:存储数据元素信息的域
指针域:存储直接后续存储位置的域
设计思路:牺牲空间效率换区时间效率。
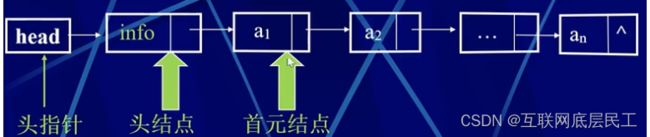
头指针:是指向链表中第一个结点(或为头结点、或为首元结点)的指针;
头结点:是在链表的首元结点之前附设的一个结点;数据域内只放空表标志和表长等信息,它不计入标长度。
首元结点:是指链表中存储线性表第一个数据元素a1的结点。
(1)什么是单链表
(2)代码定义单链表
struct LNode{ //定义单链表结点类型
ElemType data; //每个节点存放一个数据元素
struct LNode *next; //指针指向下一个节点
}
当我们需要新增一个新的节点:在内存中申请一个结点所需空间,并用指针p指向这个结点。
struct LNode *p = (struct LNode *)malloc(sizeof(struct LNode));
简化:使用typedef关键字——数据类型重命名
typedef <数据类型> <别名>
typedef struct LNode LNode; //通过typedef对数据类型重命名
LNode *p = (LNode*)malloc(sizeof(LNode))//简化
课本中定义代码
typedef struct LNode{ //定义单链表结点类型 ElemType data; //每个节点存放一个数据元素 struct LNode *next; //指针指向下一个节点 }LNode, *LinkList;等价于
struct LNode{ //定义单链表结点类型 ElemType data; //每个节点存放一个数据元素 struct LNode *next; //指针指向下一个节点 } typedef struct LNode LNode //定义一个名为LinkList的别名,它实际上是一个指向struct LNode结构体的指针。 typedef struct LNode *LinkList //创建了一个名为"LNode"的类型别名,该类型实际上是一个名为"struct LNode"的结构体类型
要表示一个单链表时,只需要声明一个头指针L,指向单链表的第一个结点。(单链表会通过指针指向下一个结点)
(3)单链表的两种实现
不带头结点的单链表
typedef struct LNode{ //定义单链表结点类型
ElemType data; //每个节点存放一个数据元素
struct LNode *next; //指针指向下一个节点
}LNode, *LinkList;
//初始化一个空的单链表
bool InitList(LinkList &L){
L = NULL; //空表,暂时还没有任何结点
return ture;
}
void test(){
LinkList L; //声明一个指向单链表的指针:头指针
//初始化一个空表
InitList(L);
//后续代码
}
//判断单链表是否为空
bool Empty(LinkList L){
if(L == NULL)
return true;
else
return false;
}
头结点:代表链表上头指针指向的第一个结点,不带有任何数据。
带头结点的单链表
typedef struct LNode{ //定义单链表结点类型
ElemType data; //每个节点存放一个数据元素
struct LNode *next; //指针指向下一个节点
}LNode, *LinkList;
//初始化一个单链表(带头结点)
bool InitList(LinkList &L){
L = (LNode *) malloc(sizeof(Lnode));//分配一个头结点
if(L==NULL) //内存不足,分配失败
return false;
L->next = NULL; //头结点之后暂时还没有结点
return ture;
}
void test(){
LinkList L; //声明一个指向单链表的指针
//初始化一个空表
InitList(L);
//后续代码
}
//判断单链表是否为空(带头结点)
bool Empty(LinkList L){
if(L->next == NULL)
return true;
else
return false;
}
对比:不带头结点写代码更麻烦。对第一个数据结点和后续数据结点的处理需要用不同的代码逻辑;对空表和非空表的处理需要用不同的代码逻辑。
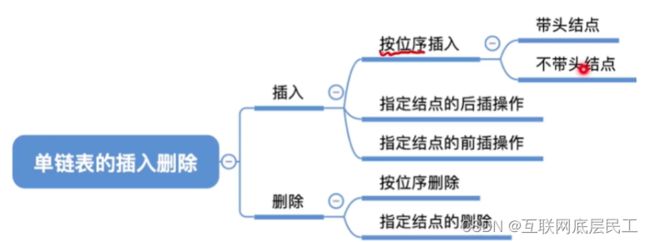
2、单链表的插入删除
(1)按位序插入(带头结点)
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。
找到第i-1个结点(前驱节点),将新结点插入其后;其中头结点可以看作第0个结点,故i=1时也适用。
typedef struct LNode{ //定义单链表结点类型
ElemType data; //每个节点存放一个数据元素
struct LNode *next; //指针指向下一个节点
}LNode, *LinkList;
//在第i个位置插入元素e(带头结点)
bool ListInsert(LinkList &L,int i,ElemType e){
//判断i的合法性,i是位序号(从1开始)
if(i<1)
return false;
LNode *p; //指针p指向当前扫描到的结点
int j=0; //当前p指向的是第几个结点
p = L; //L指向头结点,头结点是第0个结点(不存数据)
while(p!=NULL && j<i-1){ //循环找到第i-1个结点
p=p->next;
j++;
}
if(p==NULL) //i值不合法
return false;
//在第i-1个结点后插入新结点
LNode *s = (LNode *)malloc(sizeof(LNode));//申请一个结点
s->data = e;
s->next=p->next;
p->next=s; //将结点d连到p之后
return true; //插入成功
} //平均时间复杂度O(n)
(2)按位序插入(不带头结点)
ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。
找到第 i-1结点(前驱结点),将新结点插入其后;因为不带头结点,所以不存在“第0个”结点,因此 i=1时,需要特殊处理——插入(删除)第一个元素时,需要更改头指针L;
typedef struct LNode{ //定义单链表结点类型
ElemType data; //每个节点存放一个数据元素
struct LNode *next; //指针指向下一个节点
}LNode, *LinkList;
bool ListInsert(LinkList &L, int i, ElemType e){
if(i<1)
return false;
//插入到第1个位置时的操作有所不同!
if(i==1){
LNode *s = (LNode *)malloc(size of(LNode));
s->data =e;
s->next =L;
L=s; //头指针指向新结点
return true;
}
//i>1的情况与带头结点一样!唯一区别是j的初始值为1
LNode *p; //指针p指向当前扫描到的结点
int j=1; //当前p指向的是第几个结点
p = L; //L指向头结点,头结点是第0个结点(不存数据)
//循环找到第i-1个结点
while(p!=NULL && j<i-1){ //如果i>lengh, p最后会等于NULL
p = p->next; //p指向下一个结点
j++;
}
if (p==NULL) //i值不合法
return false;
//在第i-1个结点后插入新结点
LNode *s = (LNode *)malloc(sizeof(LNode)); //申请一个结点
s->data = e;
s->next = p->next;
p->next = s;
return true;
}
(3)指定结点后插入
InsertNextNode(LNode *p,ElemType e):给定一个结点p,在其之后插入元素e;
根据单链表的连接指针只能往后查找,故给定一个结点p,那么p之后的结点可知,但是p结点之前的结点无法可知。
typedef struct LNode{ //定义单链表结点类型
ElemType data; //每个节点存放一个数据元素
struct LNode *next; //指针指向下一个节点
}LNode, *LinkList;
//后插操作:在p结点之后插入元素e
bool InsertNextNode(LNode *p, ElemType e){
if(p==NULL)
return false;
LNode *s = (LNode *)malloc(sizeof(LNode));
//某些情况下分配失败,比如内存不足
if(s==NULL)
return false;
s->data = e; //用结点s保存数据元素e
s->next = p->next;
p->next = s; //将结点s连到p之后
return true;
} //平均时间复杂度 = O(1)
//有了后插操作,那么在第i个位置上插入指定元素e的代码可以改成:
bool ListInsert(LinkList &L, int i, ElemType e){
if(i<1)
return False;
LNode *p; //指针p指向当前扫描到的结点
int j=0; //当前p指向的是第几个结点
p = L; //L指向头结点,头结点是第0个结点(不存数据)
//循环找到第i-1个结点
while(p!=NULL && j<i-1){ //如果i>lengh, p最后会等于NULL
p = p->next; //p指向下一个结点
j++;
}
return InsertNextNode(p, e)
}
(4)指定结点的前插操作
//前插操作:在p结点之间插入元素e
bool InsertPriorNode(LNode *p, ElemType e){
if(p==NULL)
return false;
LNode *s = (LNode *)malloc(sizeof(LNode));
if(s==NULL) //内存分配失败
return false;
s->next=p->next;
p->next=s; //新结点s连接到p之后
s->data=p->data; //将p中元素复制到s中
p->data=e; //p中元素覆盖为e
return ture;
}//时间复杂度为O(1)
(5)按位序删除节点(带头结点)
ListDelete(&L, i, &e):删除操作,删除表L中第 i个位置的元素,并用e返回删除元素的值;
头结点视为“第0个“结点,找到第 i-1个结点,将其指针指向第 i+1个结点,并释放第 i 个结点;
typedef struct LNode{ //定义单链表结点类型
ElemType data; //每个节点存放一个数据元素
struct LNode *next; //指针指向下一个节点
}LNode, *LinkList;
bool ListDelete(LinkList &L, int i, ElenType &e){
if(i<1) return false;
LNode *p; //指针p指向当前扫描到的结点
int j=0; //当前p指向的是第几个结点
p = L; //L指向头结点,头结点是第0个结点(不存数据)
//循环找到第i-1个结点
while(p!=NULL && j<i-1){ //如果i>lengh, p最后会等于NULL
p = p->next; //p指向下一个结点
j++;
}
if(p==NULL)
return false;
if(p->next == NULL) //第i-1个结点之后已无其他结点
return false;
LNode *q = p->next; //令q指向被删除的结点
e = q->data; //用e返回被删除元素的值
p->next = q->next; //将*q结点从链中“断开”
free(q) //释放结点的存储空间
return true;
}
(6)指定结点的删除
bool DeleteNode(LNode *p){
if(p==NULL)
return false;
LNode *q = p->next; //令q指向*p的后继结点
p->data = p->next->data; //让p和后继结点交换数据域
p->next = q->next; //将*q结点从链中“断开”
free(q);
return true;
} //时间复杂度 = O(1)
3、单链表的查找
(1)按位查找
**GetElem(L, i):**按位查找操作,获取表L中第i个位置的元素的值;
LNode * GetElem(LinkList L, int i){
if(i<0) return NULL;
LNode *p; //指针p指向当前扫描到的结点
int j=0; //当前p指向的是第几个结点
p = L; //L指向头结点,头结点是第0个结点(不存数据)
while(p!=NULL && j<i){ //循环找到第i个结点
p = p->next;
j++;
}
return p; //返回p指针指向的值
}
(2)按值查找
**LocateElem(L, e):**按值查找操作,在表L中查找具有给定关键字值的元素;
LNode * LocateElem(LinkList L, ElemType e){
LNode *P = L->next; //p指向第一个结点
//从第一个结点开始查找数据域为e的结点
while(p!=NULL && p->data != e){
p = p->next;
}
return p; //找到后返回该结点指针,否则返回NULL
}
4、求单链表的长度
**Length(LinkList L):**计算单链表中数据结点(不含头结点)的个数,需要从第一个结点看是顺序依次访问表中的每个结点。算法的时间复杂度为O(n)。
int Length(LinkList L){
int len=0; //统计表长
LNode *p = L;
while(p->next != NULL){
p = p->next;
len++;
}
return len;
}