Python PyTorch3：神经网络、回归计算

1. 神经网络的结构

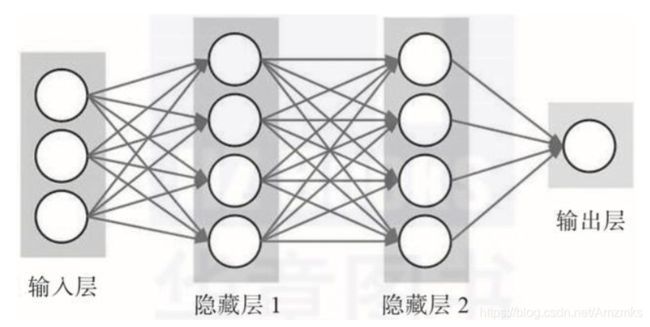
全连接（FC）网络结构是最基本的神经网络结构，每一个节点与上一层中的所有节点相连接。

BP神经网络由输入层、隐藏层和输出层组成。输入层和输出层的节点数取决于问题需要的输出和输出变量的个数，隐藏层节点数需要由开发者进行调试。

在神经网络中，只有数据非线性分离时才需要隐藏层。对于一般的数据集，1~2层隐藏层已经足够了。

隐藏层中的神经元数量由开发者调试获得。在隐藏层中使用太少的神经元将导致欠拟合。相反，使用过多的神经元可能会导致过拟合等问题。选择合适的隐藏层神经元数量至关重要。通常情况下，对所有隐藏层使用相同数量的神经元。与在每一层中添加更多的神经元相比，添加层数将获得更大的性能提升。因此，不要在一个隐藏层中加入过多的神经元。

2. 线性回归

PyTorch中使用torch.nn创建一个神经网络。自定义的神经网络继承nn.Module类。nn.Module包含神经层。在神经网络类的init构造函数中定义网络结构，forward(input)可以用来返回output输出结果。

import numpy as np
import matplotlib.pyplot as plt
from torch import nn, optim
from torch.autograd import Variable
import torch

# 创建线性函数+噪声
x_data = np.random.rand(100)
noise = np.random.normal(0, 0.01, x_data.shape)
y_data = x_data * 0.1 + 0.2 + noise

# PyTorch需要传入2维数据
x_data = x_data.reshape(-1, 1)
y_data = y_data.reshape(-1, 1)

# 把numpy数据变成tensor
x_data = torch.FloatTensor(x_data)
y_data = torch.FloatTensor(y_data)
# 将tensor转为pytorch的变量 数据的输入
inputs = Variable(x_data)
# 将tensor转为pytorch的变量 数据的目标值 输出
target = Variable(y_data)


# 构建神经网络模型
# 类名可以随便取，需要继承torch.nn.Module类
class LinearRegression(nn.Module):
    # 初始化方法，定义网络结构
    # 一般把网络中具有可学习参数的层放在__init__()中
    def __init__(self):
        # 初始化nn.Module父类
        super(LinearRegression, self).__init__()
        # 全连接层
        # 输入1个神经元（x），输出1个神经元（y）
        self.fc = nn.Linear(1, 1)

    # 定义网络计算
    def forward(self, x):
        # 将x传入全连接层做计算
        out = self.fc(x)
        return out


# 定义模型
model = LinearRegression()
# 定义代价函数
mse_loss = nn.MSELoss()
# 定义优化器 lr学习率
optimizer = optim.SGD(model.parameters(), lr=0.1)

# 循环模型参数的名称和数值，包括权值和偏置值
for name, parameters in model.named_parameters():
    print('name:{}, param:{}'.format(name, parameters))

# 训练循环1001次
for i in range(1001):
    out = model(inputs)
    # 计算loss
    loss = mse_loss(out, target)
    # 梯度清0
    optimizer.zero_grad()
    # 计算梯度
    loss.backward()
    # 修改权值
    optimizer.step()
    if i % 200 == 0:
        print(i, loss.item())

# 将inputs传给模型得到预测值
y_pred = model(inputs)
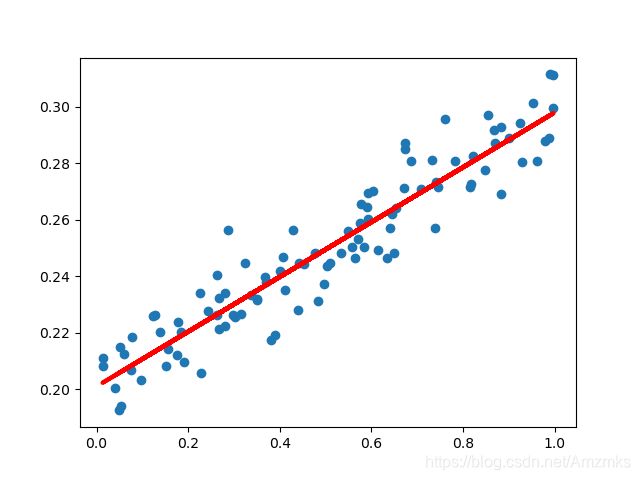
plt.scatter(x_data, y_data)
plt.plot(x_data, y_pred.data.numpy(), 'r-', lw=3)
plt.show()

输出：

name:fc.weight, param:Parameter containing:
tensor([[0.4561]], requires_grad=True)
name:fc.bias, param:Parameter containing:
tensor([0.7357], requires_grad=True)
0 0.5190306901931763
200 9.697255882201716e-05
400 9.521372703602538e-05
600 9.520256571704522e-05
800 9.520251478534192e-05
1000 9.520247840555385e-05

3. 非线性回归

import numpy as np
import matplotlib.pyplot as plt
from torch import nn, optim
from torch.autograd import Variable
import torch

# 创建非线性函数+噪声
x_data = np.linspace(-2, 2, 200)
noise = np.random.normal(0, 0.2, x_data.shape)
y_data = np.square(x_data) + noise

x_data = x_data.reshape(-1, 1)
y_data = y_data.reshape(-1, 1)

# 把numpy数据变成tensor
x_data = torch.FloatTensor(x_data)
y_data = torch.FloatTensor(y_data)
inputs = Variable(x_data)
target = Variable(y_data)


# 构建神经网络模型
# 一般把网络中具有可学习参数的层放在__init__()中
class LinearRegression(nn.Module):
    # 定义网络结构
    def __init__(self):
        # 初始化nn.Module
        super(LinearRegression, self).__init__()
        # 非线性回归需要加隐藏层
        # 输入1个神经元，输出10个神经元
        self.fc1 = nn.Linear(1, 10)
        # 非线性回归需要加入隐藏层，隐藏层的意义就是把输入数据的特征，抽象到另一个维度空间，来展现其更抽象化的特征，这些特征能更好的进行线性划分。
        # 在隐藏层中加入tanh激活函数
        self.tanh = nn.Tanh()
        # 输入10个神经元，输出1个神经元
        self.fc2 = nn.Linear(10, 1)

    # 定义网络计算
    def forward(self, x):
        x = self.fc1(x)
        x = self.tanh(x)
        x = self.fc2(x)
        return x


# 定义模型
model = LinearRegression()
# 定义代价函数
mse_loss = nn.MSELoss()
# 定义优化器
optimizer = optim.SGD(model.parameters(), lr=0.3)

for name, parameters in model.named_parameters():
    print('name:{}, param:{}'.format(name, parameters))

for i in range(2001):
    out = model(inputs)
    # 计算loss
    loss = mse_loss(out, target)
    # 梯度清0
    optimizer.zero_grad()
    # 计算梯度
    loss.backward()
    # 修改权值
    optimizer.step()
    if i % 200 == 0:
        print(i, loss.item())

y_pred = model(inputs)
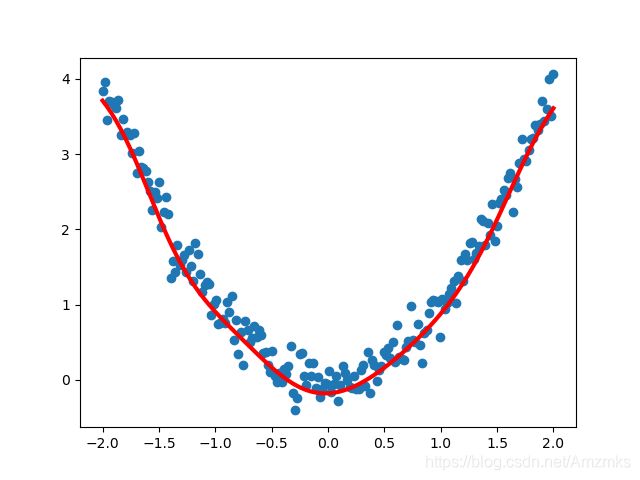
plt.scatter(x_data, y_data)
plt.plot(x_data, y_pred.data.numpy(), 'r-', lw=3)
plt.show()

输出：

name:fc1.weight, param:Parameter containing:
tensor([[-0.5076],
        [-0.2512],
        [ 0.3506],
        [-0.3037],
        [ 0.9912],
        [ 0.3866],
        [ 0.1229],
        [ 0.2591],
        [ 0.3712],
        [ 0.8306]], requires_grad=True)
name:fc1.bias, param:Parameter containing:
tensor([-0.0394,  0.7240, -0.5776,  0.7237, -0.0722, -0.7205,  0.9501, -0.1061,
         0.2135, -0.9476], requires_grad=True)
name:fc2.weight, param:Parameter containing:
tensor([[-0.0502, -0.1002,  0.2274, -0.2604,  0.2435,  0.3001,  0.0657, -0.0459,
         -0.2467, -0.2012]], requires_grad=True)
name:fc2.bias, param:Parameter containing:
tensor([0.2703], requires_grad=True)
0 3.604307174682617
200 0.07464659959077835
400 0.09846562147140503
600 0.08561816811561584
800 0.0697840079665184
1000 0.058194875717163086
1200 0.05261123552918434
1400 0.0494537353515625
1600 0.04836893081665039
1800 0.048560041934251785
2000 0.04887966811656952